考虑虚拟电厂的分布式电源优化配置研究

马立红，肖禹 ，宁光涛，王海生，李思凡，吕懿

（1.海南电网有限责任公司，海南 海口 570203；2.北京国科恒通科技股份有限公司，北京 100085）

随着国家可持续发展战略不断推进，研究人员对分布式电源（distributed generation，DG）技术的研究也不断深入和加强，越来越多的国家将可再生能源利用纳入电力系统建设的规划和优化[1]。据预测分析，自2010年到2035年可再生能源的发电量将会实现2.7倍的增长[2]。随着分布式电源的大量并网，虚拟电厂（virtual power plant，VPP）也应运而生。虚拟电厂是一种灵活的分布式电源聚合体[3]。虚拟电厂可利用风电、光电等多种能源形式的可再生能源，通过通信手段将指定区域内的分布式电源、储能装置等结合到一起，在控制中心对多种信息进行汇总分析，将其作为一个综合体接入到电网中运行。虚拟电厂电源通常具有很强的环保特性，污染排放几乎为零。但是由于这些电源同时具有很强的随机波动性，易受外界环境影响，虚拟电厂的运行表现出伸缩特性，因此需要配电网进行合理规划，协调虚拟电厂运行，达到削峰填谷、提高电能质量等积极效果[4]。

随着分布式电源技术的不断发展，虚拟电厂已经成为业界国内外学者研究的重点。文献[5]以光伏发电、风电、储能系统和燃气轮机为电源，与需求响应共同构建虚拟电厂模型，引入风险条件值理论和置信度来描述虚拟电厂运行不确定性，并将运营收益最大化作为目标函数，建立虚拟电厂的优化调度模型。文献[6]是以虚拟电厂利益最大化、成本最小化为目标，对虚拟电厂调度进行优化。文献[7]为减少网络阻塞和功率不平衡，提出一种优化算法，可通过虚拟电厂管理范围内的可控负荷和分布式电源来最小化负荷大小。文献[8]根据实时价格，通过信息融合算法提出一种虚拟电厂的定价控制方案。文献[9]建立了关于分布式电源、储能、可中断负荷的虚拟电厂模型，使用象群放牧优化算法解决了参与日前市场的资源调度利润优化问题。文献[10]建立了最优需求响应模型优化虚拟电厂和电网的互动，并提出模糊控制方法以考虑可再生能源的不确定性。

在配电网和虚拟电厂相互协作的基础上，虚拟电厂和配电网相互影响，具有不同的优化意义。关于虚拟电厂的优化研究大多建立在虚拟电厂侧，以虚拟电厂的最大利益为目标，而配电网侧的相关优化较少。虚拟电厂电源的大量接入，由于位置容量固定，在运行过程中很可能会对配电网的可靠性、网损以及配电网的电能质量产生影响。本文使用标准算例对虚拟电厂电源接入配电网进行仿真，分析了虚拟电厂电源接入带来的不利影响，建立电能质量优化多目标模型，提出了一种粒子群与差分进化（particle swarm optimization-differertion evolution，PSODE）混合算法，并使用改进的PSO-DE优化算法，通过配电网层面的分布式电源优化配置，调节电压，提升电能质量，为分布式电源大量接入背景下的配电网规划提供科学参考。

1 虚拟电厂接入影响仿真分析

采用IEEE37节点测试系统算例进行虚拟电厂电源对配电网影响的仿真分析[11]，其配电系统如图1所示。该系统基准电压为4.18 kV，系统容量为 2.588 MV·A，总负荷为 2.457 MW+1.201 Mvar。系统负载为点负载，且非常不对称，线路始端负荷较重，末端负荷较轻，此时线路中网损为152.4 kW。

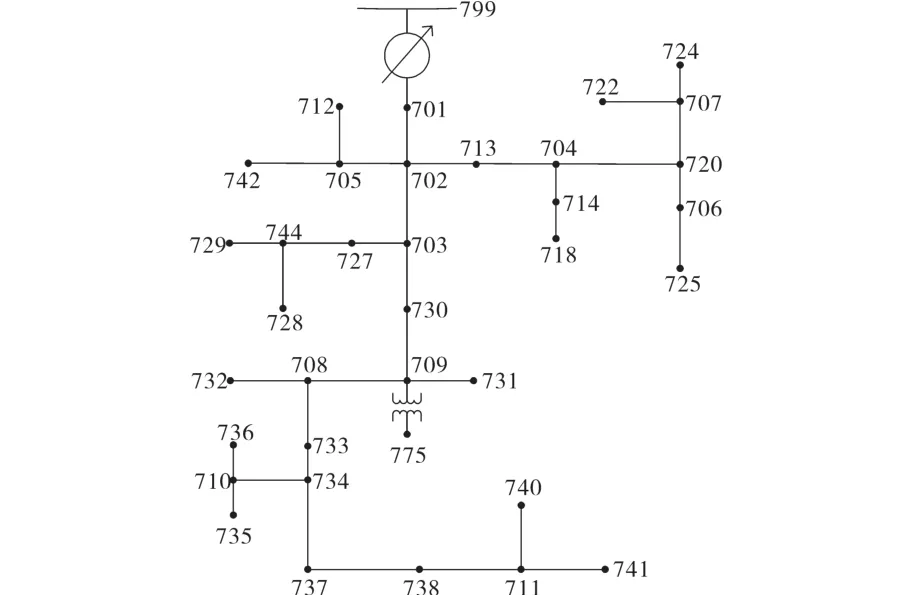
图1 IEEE37节点配电系统Fig.1 IEEE37 node power distribution system

在IEEE37节点配电系统中接入虚拟电厂电源，在735节点和729节点分别接入一个600 kW的光伏，在704节点接入一个1 000 kW的储能，在724节点和731节点接入两个600 kW的风电。虚拟电厂电源接入后，线路中网损为42 W，大大减小了网络损耗，其网络损耗变化如图2所示，颜色深的部分为网损大的地方，浅的地方为网损小的地方。在虚拟电厂电源接入之前，线路首端的网损较大，主干线路的线损较大，在虚拟电厂电源接入后，可以明显看到主干线路的线损变小，配电网中的网损主要分布在光伏和风电接入的节点附近。由此可见，虚拟电厂电源的接入改变了原系统中的网损分布，且明显降低了系统的网损。

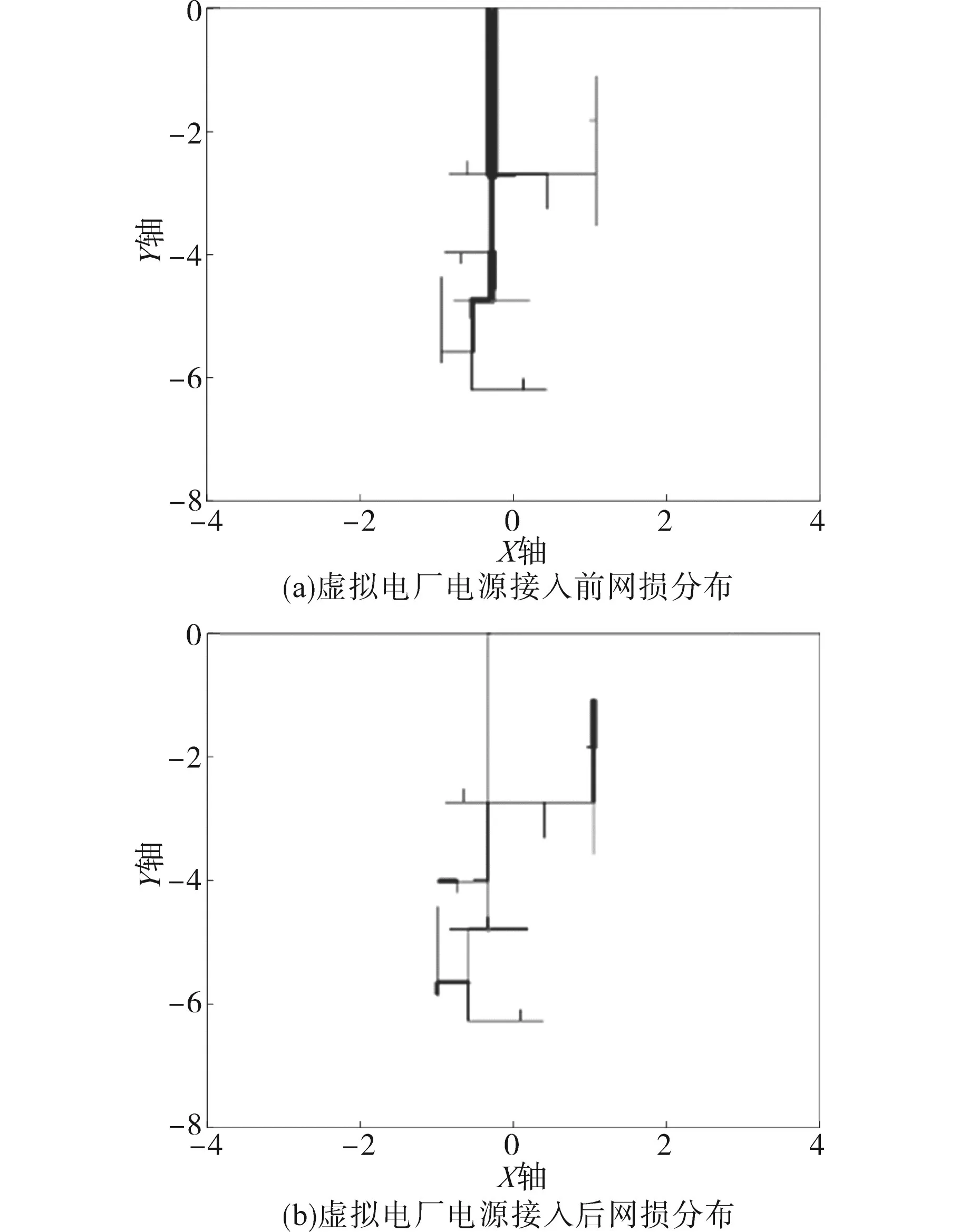
图2 虚拟电厂电源接入前后的网损分布对比Fig.2 Comparison of network loss distribution before and after the virtual power plant power supply is connected

图3为接入虚拟电厂电源前后的电压对比图。在虚拟电厂接入电网运行后，多数节点电压相较未接入电网前电压都有所降低。图4为虚拟电厂电源电压畸变率在接入电网前后的状态变化，分析可知，在虚拟电源接入电网后，虚拟电厂中电源电压畸变率提升了3倍。由此可见，虚拟电厂（含有风电）电源的接入明显降低了配电系统的电压质量。

图3 虚拟电厂电源接入前后的电压对比Fig.3 Comparison of voltage before and after power connection of virtual power plant

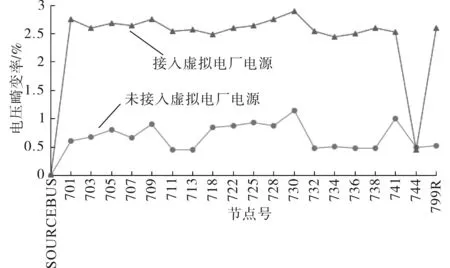
图4 虚拟电厂电源接入前后的电压畸变率对比Fig.4 Comparison of voltage distortion rate before and after power connection of virtual power plant

2 PSO-DE算法

2.1 粒子群算法

粒子群（PSO）算法参数简单，容易实现，可通过粒子规模、学习因子以及惯性权重来促进算法性能[12]。其中，学习因子作为最重要的可调参数，通常也是算法改进的首选。对学习因子进行动态更新，使其与迭代次数相关，更新公式如下：

式中：gen为当前迭代次数；gpso为粒子群的最大迭代次数。

2.2 差分进化算法

差分进化（DE）算法基本原理是基于生物仿生学，具有一定的自组织自学习能力，改进方向包括控制参数、进化模式等[13]。但DE算法的优化步骤较为简单，随着迭代次数的增加，算法容易过早进入局部最优状态，收敛速度也较为缓慢。因此可以将其与收敛较快的PSO算法结合，形成一种新的算法。

2.3 PSO-DE算法

对于PSO和DE算法已经有了多种改进，对于将两种算法的结合也有相关研究。文献[14]将种群分为并行的PSO群和DE群，将两个子群得到的种群最优值作为下一代的进化依据；文献[15]根据PSO和DE算法的特点，将两种算法进行混合，在每次迭代结束后进行比较，得出最优个体。以上文献资料表明，PSO-DE算法在全局搜索能力和收敛速度方面比单个的PSO和DE算法效率更高。

本文将PSO算法进行改进后，与DE算法进行结合，并且将结合后的结果进行优化，得出PSO算法的适应度函数，再对DE算法中的杂交概率和缩放因子进行寻优计算，从而得出PSO-DE优化算法。该PSO-DE优化算法的具体操作流程如图5所示，步骤如下：

图5 PSO-DE参数优化算法流程图Fig.5 Flow chart of PSO-DE parameter optimization algorithm

1）初始化粒子种群。同时设定PSO算法种群个数m=40，惯性权重w=0.7，学习因子如式（1），最大迭代次数为gpso=100，粒子1的取值范围对应DE算法的变异参数F0，粒子2的取值范围对应DE算法的交叉参数CR；

2）引入DE算法，其目标函数为最终的目标函数，计算初始种群的适应度；

3）更新学习因子，并对当代粒子进行速度、位置更新；

4）竞争操作；

5）利用新种群重复以上步骤，直至满足最大迭代次数。

2.4 算法测试

使用某分布式光伏接入线路进行算法测试，PSO-DE优化算法拓扑图[16]如图6所示。线路中在节点 3，5，7，9，13，15，17，19，21和节点 23接入负荷，总负荷为9 260 kW，在节点11接入了5 600 kW的分布式光伏。

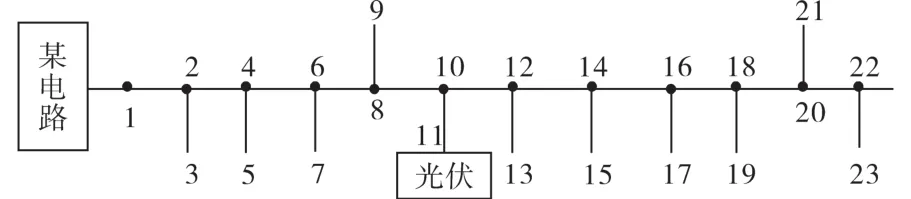
图6 PSO-DE优化算法拓扑图Fig.6 Topology diagram of PSO-DE optimization algorithm

以网络损耗最小、投资费用最低以及电压质量最优为目标函数。其中，网络损耗最小以电能传输中的能量损耗最小为目标；投资费用最低以线路建设过程中所需要投入的总成本最低为目标，成本需要考虑线路的长度、地理位置和环境、施工条件等多个因素；电压质量以电压畸变率和线路的潮流分布图来进行衡量，以电压稳定性最好为质量最优的评价标准。

根据文献[17]中的多目标归一化确定各自的权重，得出网络损耗最小、投资费用最低以及电压质量最优的权重分别为0.3，0.4，0.3。分别采用PSO算法、DE算法及PSO-DE优化算法对线路中分布式光伏进行容量优化，表1为3个算法的优化结果。

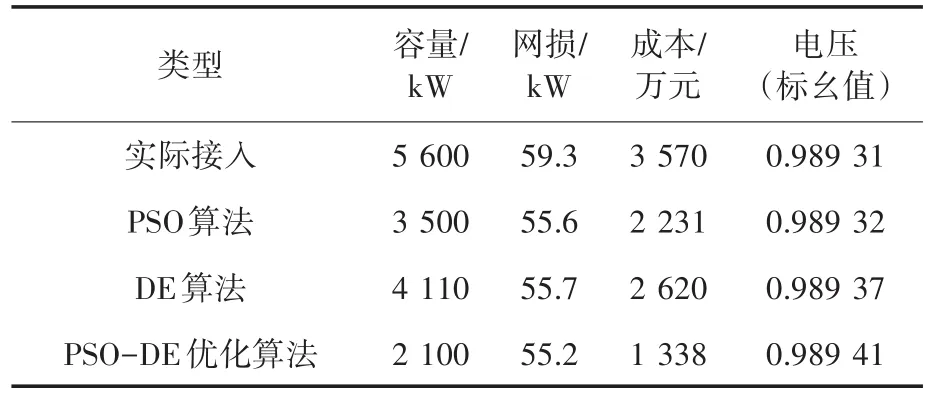
表1 优化结果比较Tab.1 Comparison of optimization results

由表1可知，PSO-DE优化算法的优化结果网损最低、成本最低，而节点电压平均值也最高。与实际接入光伏相比，网损减少4.1 kW，成本也降低2 232万元，证明PSO-DE算法可以应用于分布式光伏的选址定容优化中，且优化效果良好。

3 考虑虚拟电厂的DG选址定容优化

配电网中接入虚拟电厂电源可以有效降低网损，调节线路潮流分布。但是对于电能质量，虚拟电厂电源的接入不仅会引起电压波动，可能还会引起电压下降，增加谐波污染，给配电网带来不利影响。而对于分布式电源的大量接入，可以从配网侧优化新增分布式电源种类与配置，增加电网对分布式电源的消纳能力，提高电网可靠性。本节以优化电能质量为目标，对配电网中分布式光伏接入进行选址定容研究。

3.1 目标函数的确定

本文以分布式光伏电站为例，以电压偏差和电压畸变率为目标，进行分布式光伏的选址定容优化。其目标函数如下：

1）电压偏差最小。电压偏差指的是实际电压与额定电压的差值，可用有名值或标幺值表示。电压偏差越小，证明电压质量越好。其表达式为

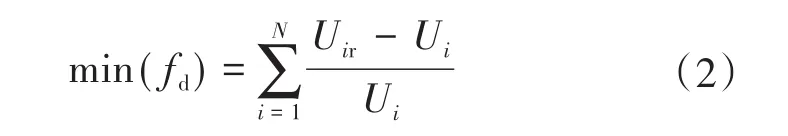
式中：Uir为节点i的额定电压；Ui为实际电压；N为线路中所有节点数目。

2）电压畸变率最小。谐波失真对电能质量有着很大影响，电压畸变率表示谐波失真的程度，指的是各次谐波电压的平方和的均方根与基波电压的比值，用百分数表示。其表达式为

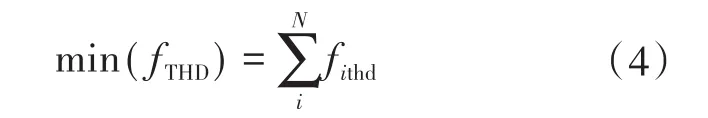
式中：uin为节点i在n次频率上的电压；fithd为节点i的电压畸变率；fTHD为所有节点电压畸变率的和。

3.2 非指定权重多目标优化

将多个目标转化为一个目标，不需要通过权重系数法[18]来指定具体的目标，可以先对存在的电压偏差做出纠正处理，再进行其他的计算，处理后的目标值v(ak)如下式所示：

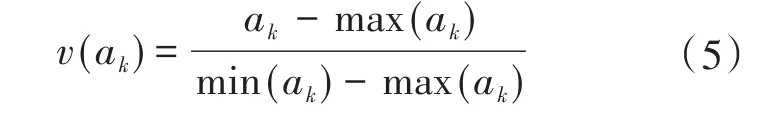
式中：ak为单目标函数；max(ak)为ak的最大值；min(ak)为ak的最小值。

转化成多目标函数fitness为

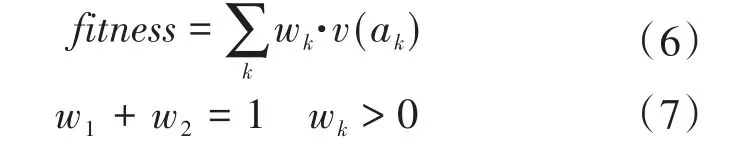
式中：wk为单一目标函数的权重系数。

作为非精确包含信息对双目标进行优化，使其构建一种包含电压偏差和电压畸变率综合最小的数学模型。

3.3 约束条件

1）功率平衡约束如下式所示：

式中：Ps，Qs为平衡节点注入的有功、无功功率；Pi,PV，Qi,PV为节点 i光伏注入有功、无功功率；Pload，Qload为系统总负荷；Ploss，Qloss为系统总网损。

2）容量约束如下式所示：

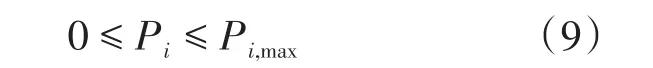
式中：Pi,max为任一节点允许接入分布式光伏最大容量。

3）节点电压约束如下式所示：

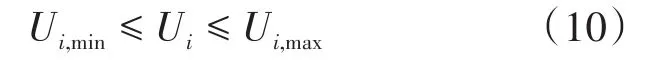
式中：Ui,min，Ui,max分别为任一节点电压的最小值与最大值。

4）渗透率约束。需要合理设置接入容量的大小，避免由于PV的接入给系统潮流造成影响。渗透率如下：

4 算例仿真

以接入虚拟电厂电源的IEEE37节点测试系统为算例，以式（6）的目标函数和式（8）～式（11）的约束条件共同构成光伏接入选址定容优化模型，使用提出的PSO-DE优化算法进行求解。仿真优化在Matlab中调用OpenDSS接口实现。其过程如下：

1）初始化DE算法中种群，将目标函数代入适应度函数，计算个体的适应度；

2）通过当代适应度更新PSO算法中的学习因子，经过PSO算法优化得到DE算法中的缩放因子和交叉参数，随后继续变异、交叉操作；

3）得到新种群，重复步骤2），直至满足最大迭代次数。

分布式光伏的位置优化同上，与容量优化不同的是，位置的选择范围是1～35个不同的自然数（自然数代表节点编号）。

经过优化后，得到IEEE37节点配电系统中安装配网侧分布式光伏的最佳配置方案为：在720节点接入255 kW的分布式光伏，此时线路网损为45.2 kW。优化前、后的节点电压对比如图7所示。由图7可知，优化后的节点电压相较于优化之前提升了0.05（标幺值）左右，且节点电压的大小趋势相同。

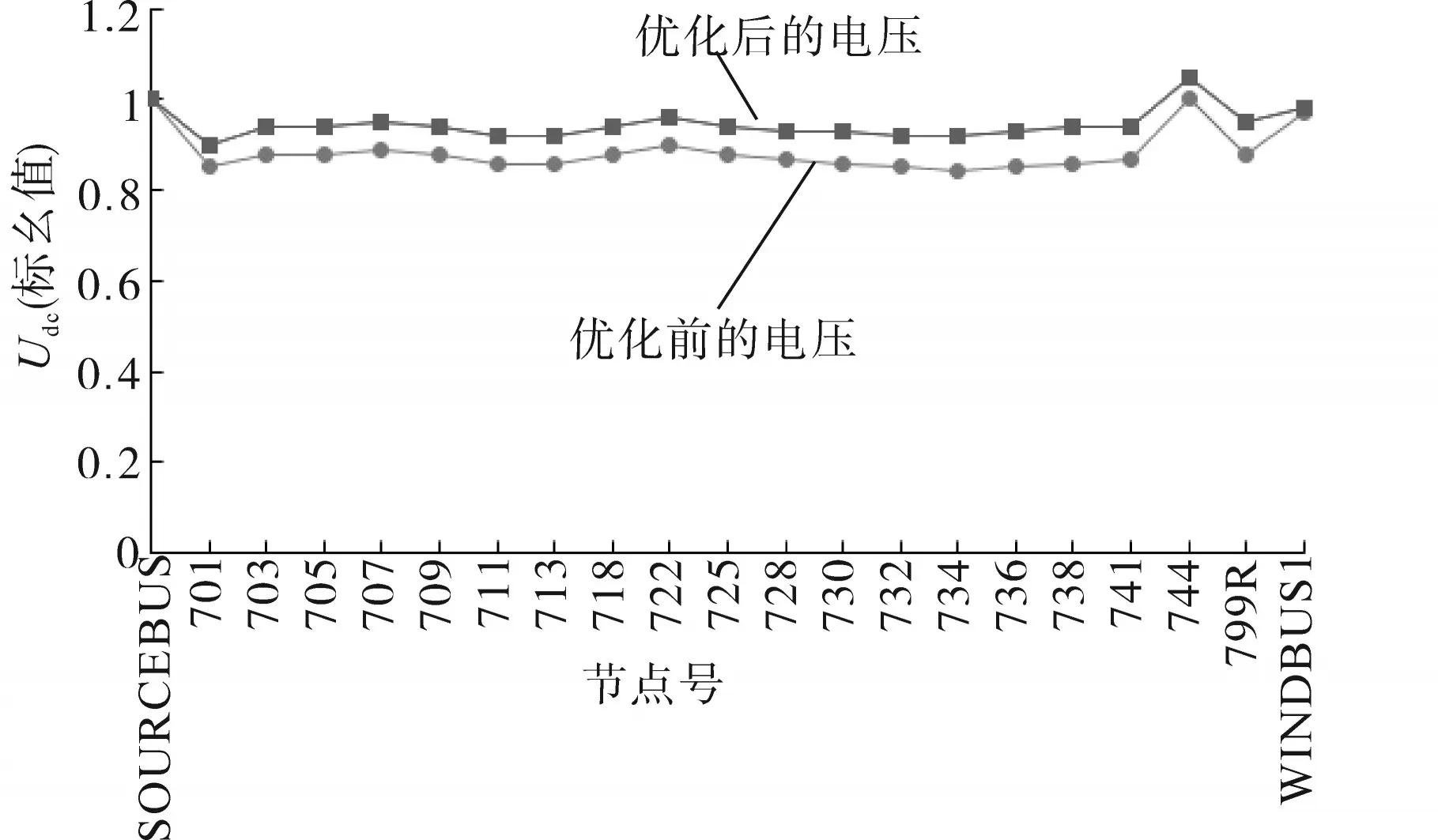
图7 优化前、后的节点电压对比图Fig.7 Comparison of node voltages before and after optimization

图8为优化前、后的节点电压畸变率对比图。由图8看出，优化后电压畸变率较优化前接入虚拟电厂电源时有明显下降，但是较未接入虚拟电厂电源时的电压畸变率偏大。

图8 优化前、后的节点电压畸变率对比图Fig.8 Comparison of node voltage distortion rate before and after optimization

图9为优化前、后线路的潮流分布对比图。相较于虚拟电厂电源接入后的潮流分布，中间主干线路的颜色变浅，说明分布式光伏的接入有效减轻了线路负荷；与优化前相比，网损总量由42 kW变成了45.2 kW，有少许上升，但是由于优化以提升电能质量为目标，网损的少量增加产生的影响近乎忽略不计。

图9 优化前、后的潮流分布图Fig.9 Power flow distribution map before and after optimization

5 结论

针对分布式电源大量接入配电网引起的电能质量问题，本文研究了考虑虚拟电厂的分布式电源优化配置，主要完成如下工作：

1）使用IEEE37节点测试算例进行虚拟电厂接入仿真分析，研究了虚拟电厂电源接入后对配电网潮流、网损以及谐波3个方面的影响；

2）考虑对配电网电压质量影响，对于分布式电源接入配电网的选址定容问题，建立以电压偏差和畸变率综合最优为目标的电能质量优化模型；

3）对传统粒子群算法进行了改进，针对分布式电源选址定容提出了一种基于PSO算法和DE算法的PSO-DE优化算法，并通过实际分布式光伏优化算例进行测试验证；

4）考虑虚拟电厂接入影响，利用建立的电能质量优化模型和提出的PSO-DE优化算法，以IEEE37节点测试系统为例研究了配网侧新增分布式光伏接入配电网选址定容问题。结果表明：优化后的电压畸变率较接入虚拟电厂电源未优化前明显下降，但较未接入虚拟电厂电源的电压畸变率偏大；优化后的分布式光伏的接入有效减轻了线路负荷。该仿真算例结果可为分布式电源接入配电网提供科学的参考依据。