综合能源系统中多能源协同优化方法研究

武志宏，杨永标，李熙，李泽斌，张卫国

（1.国网山西省电力公司，山西 太原 030000；2.东南大学电气工程学院，江苏 南京 210096；3.国网山西省综合能源服务有限公司，山西 太原 030000；4.国网太原供电公司，山西 太原 030000；5.国电南瑞科技股份有限公司，江苏 南京 210008）

能源作为人类社会进步的关键物质基础之一，在经济发展与国民保障等方面均发挥着重要作用。其中，综合能源系统中多能源协同规划和调控方式的研究，会对能源生产与能源生产范式重构等方面有创新的作用，并充分丰富综合能源系统的整体建设和能源互联网的覆盖，以此推动能源绿色生态化发展，为能源高效利用和节能减排提供支撑[1-3]。

鉴于综合能源中多能源协同优化的现实意义，该领域相关人员提出了很多优秀成果。文献[4]指出综合能源系统中的各种设备日益丰富的现状，提出将区域能源的运营商当作主体，分别在系统侧与用户侧同时通过综合能源系统具备的多能互补性，设计并构建双侧系统运行模型，调整能源转换设备分配因素，实现系统多能源需求匹配度的有效提升，但该方法的可靠性较低；文献[5]指出工业园区是一个比较典型的综合能源系统，将能量梯级应用至综合能源系统中进行多能源调节与优化，先简单介绍了工厂综合能源系统框架，然后针对能源系统中各种能量生产设备和能量转换设备等进行单独建模，但是该方法的实际应用成本较高；文献[6]指出将综合能源系统当作核心的综合能源互联网为生态环境污染治理的关键途径之一，将社区的综合能源系统当作研究目标对象，提出构建包括共享储能和热电联供等设备的用户协调模型，依据用户日消耗量科学再分配整体费用，但是该方法的减排率受到限制。

上述研究的减排性能和模型可靠性待优化，为了更好地实现综合能源协同优化，减少能源消耗成本，增强系统可靠性，提高减排率，本文提出基于混沌蛙跳算法的综合能源系统中多能源协同优化方法。利用混沌蛙跳算法具备的快速寻优性能逐渐向理论最优解逼近，根据自适应网格密度法动态维护最优解规模，通过最优解选取方案为蛙群选取最佳的更新粒子，当满足得到最优解或达到最大迭代次数条件时，获取最优解，得到符合目标模型的多能源协同优化方案，以缓解综合能源系统中多能源协同优化的问题，为该领域相关研究提供参考。

1 综合能源系统中多能源协同优化

1.1 目标函数

综合考虑多能源协同优化实际需求，依靠综合能源系统基本结构图构建多能源协同优化模型，结构图如图1所示。

图1 综合能源系统基本结构图Fig.1 Basic structure of integrated energy system

综合能源系统是面向整个社会能源市场与供电市场的，针对目前用户所拥有电力、天然气、供热等能源，通过大数据的控制将其转换为用户交互能源提供保障，其中煤炭和火力发电是具有波动性、间歇性和不确定性的不再生能源发电，风力就近消纳发电等为可再生能源发电。覆盖城镇范围的整体综合能源系统是自底而上的以用户为中心的结构，而用户侧除电能外，更是拥有气、冷、热等多种能源形式，因此需要多能综合响应。以下列几方面为主要目标函数进行构建。

1.1.1 系统总费用最低

在多能源系统优化过程中，能源调度周期的总时段数量T内，总费用Ctotal,T由周期内生产运行维护成本和清洁机组补偿费以及向电网净购电费构成，即

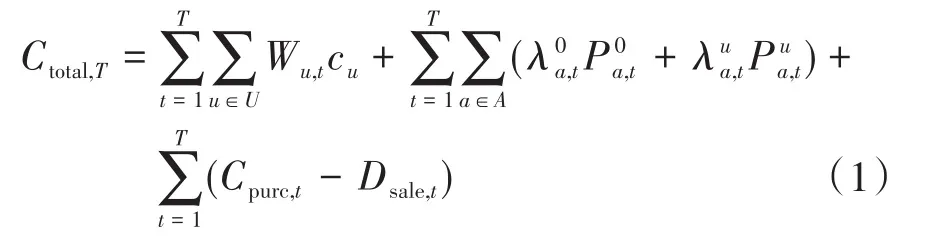
式中：U为综合能源系统中各设备集合；Wu,t为设备u在t时段内供能；cu为u单位供能成本；A为清洁机组集合；为机组a由于过度调度导致的缺电量，在固定的时间t内，表示可使用电量值与需求调度电量的和；为机组a过度调度过程中的补偿系数；为机组a由于欠调度导致的窝电量，表示可使用电量值与需求调度电量的差；为机组a欠调度过程中的补偿系数；Cpurc,t为t时段购电费；Dsale,t为t时段售电所得收入。

1.1.2 系统可靠性最强

综合能源系统缺电率（loss of power supply probability，LPSP）为额定周期范围内系统缺供电量在该周期系统总需电量中占据的比例。LPSP为供电的可靠性因素，引入综合能源系统所包含的电源类型，LPSP的计算式为

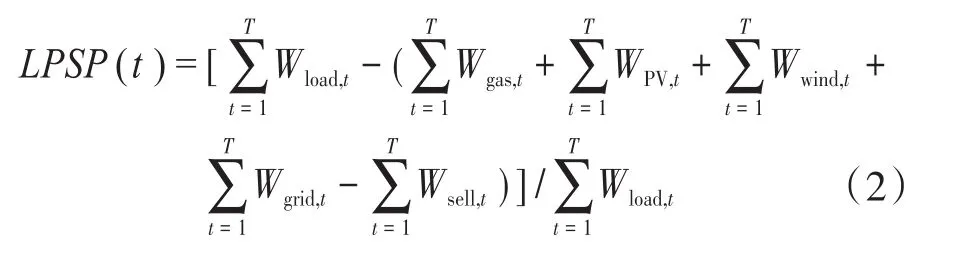
式中：Wload,t为t时段综合能源系统中电量需求；Wgas,t，WPV,t，Wwind,t，Wgrid,t分别为 t时段燃气机组、光伏、风机发电量以及向主网购买的电量；Wsell,t为t时段向主网售电总量。

1.1.3 系统减排率最高

综合能源系统中减排率是系统与传统天然气联供发电相比的污染减排率，其表达式为

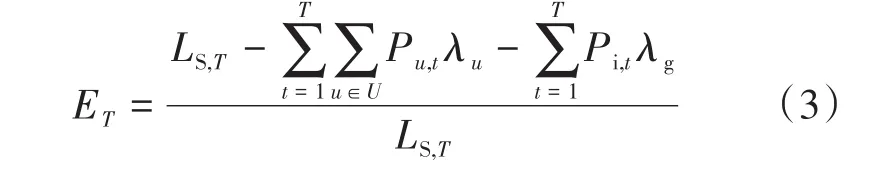
式中：ET为在时段T内减排率；LS,T为传统天然气联供发电污染排放量；Pu,t为设备u在t时段等效发电总量；λu为设备u等效污染排放系数；Pi,t为t时段和电网之间交换电量；λg为电网侧供电过程中污染排放系数。

1.2 约束条件

1.2.1 可靠性约束

当供电整体可靠程度为一定时，想进一步提高可靠性要以增加成本与提高能耗为代价。融合当前宏观的发展趋势，单纯追求系统供电程度最高并不是最好的选择。综上，在综合考虑电量均衡性过程中，不一定要求机组出力和主网购电相加结果必须不小于负荷，而是以可靠程度当作目标实行优化。然而依据国家有关规定[7]，要为供电可靠程度设计一个下限值，融合相关指标，LPSP不可高于上限，则有：

1.2.2 热量均衡约束

该约束中包含冷、热均衡两部分，其物理概念为：由各热源得到的热量在考量了设备效率与有关损耗之后，分别全部转换成冷、热负荷。

热均衡约束表达式为

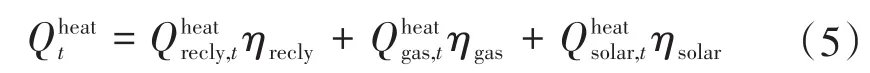
冷均衡约束条件表达式为

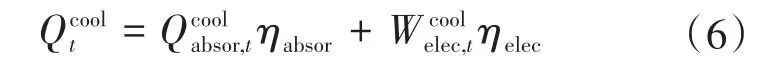
1.2.3 设备运行约束条件

1）光伏机组运行。综合能源系统中光伏机组出力上限值为某时段当地太阳能光伏机组额定装机容量值、太阳能板的总面积以及太阳能转化效率乘积值，即机组运行电功率，其小于机组额定功率值[8-10]。调度过程中一旦有需要，则利用弃光实现光伏机组出力低化，然而一定要保障其出力高于最小限额。综上有：

式中：PPV(t)为t时段光伏机组运行电功率；Pcapa为光伏机组额定装机容量值；ηPV为太阳能转换效率；SPV为太阳能板面积；P_PV，PˉPV(t)为光伏机组最小与最大的发电功率值。

2）天然气的内燃机组。机组出力过程中应该在上、下限中间，且机组功率变化率会受到爬坡率约束，则有：

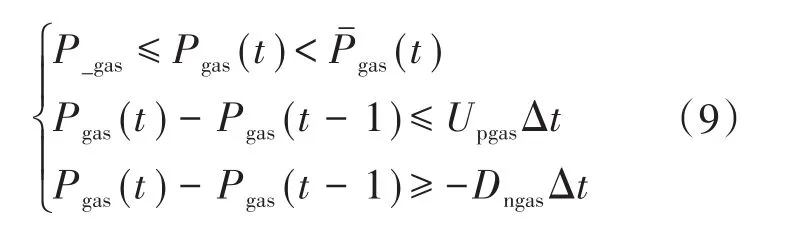
式中：Pgas(t)为t时段燃气机发电功率值；P_gas，(t)分别为燃气机最小、最大的发电功率值；Upgas，Dngas分别为燃气机向上、向下的爬坡速率。

3）风力发电机组。该机组约束物理定义和光伏雷同，但是处理的上限和气象条件存在分段函数相关性[11-13]，则有：

式中：Pwind(t)为t时段风电机组总发电功率；P_wind，分别为风电机组最小、最大发电功率；Prate为机组额定输出功率；v(t)为风速函数；vin，vout分别为切入、切出风速；vrate为额定风速。

4）制冷机组。吸收形式的制冷机器与电制冷机功率值一定要为正，同时不可超过功率上限值，则有：

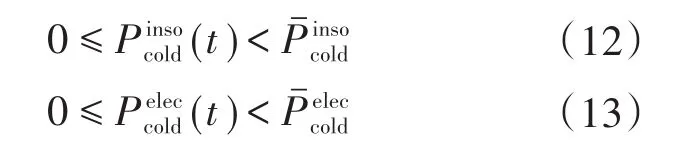
1.3 基于混沌蛙跳算法的多能源协同优化

为了在约束条件下对目标函数进行求解，引入混沌蛙跳算法，详细过程如下。

1.3.1 自适应网格密度

假设Pareto代表最优解的存储器，将其记作Archive集，混沌蛙跳算法每次进化所得粒子当作Archive集候选解，在候选解满足下列条件之一即能够进入Archive集：

条件1：Archive集是空集；

条件2：Archive集是非空集合，同时候选解不被Archive集中任何一个粒子所支配；

条件3：候选解支配Archive集中的所有粒子[14-16]。

假设不对Archive集规模进行控制，会在很大程度上提高计算复杂度，综上，将Archive集规模定义为N′，同时根据自适应网格密度法对Archive集规模进行动态维护[17]。自适应网格密度法详细运行流程图如图2所示。

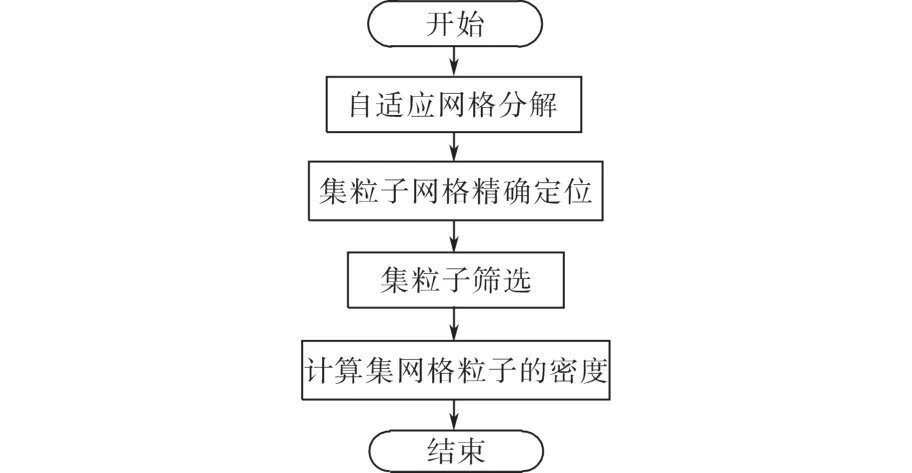
图2 适应网格密度法详细运行流程图Fig.2 Detailed operation flow chart of adaptive grid density method

根据以下步骤进行自适应网格密度分析：

步骤1：自适应网格分解。将m′维目标空间分解成K'1× K'2× … × K'm′同样的网格[18-19]，其中，网格i维宽度值d'i表达式为

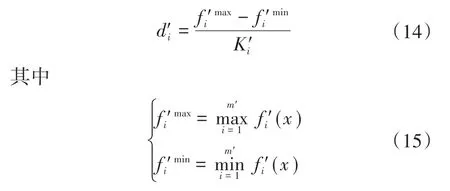
步骤2：Archive集粒子网格精确定位。假设第t′代Archive集为A't′={a'1,…,a'j,…,a'h}，h ≤ N′，针对a'j，其第i维网格编码wji表达式为

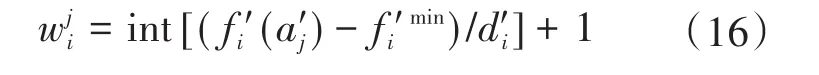
根据式（16）能够确定a'j在目标范围内位置。

步骤3：对Archive集网格粒子的密度进行计算。设定网格 Gk′粒子密度值是 D'k′，同时将 D'k′设置成网格内Pareto最优解的数量，假设网格内部不存在粒子，则 D'k′=0。

步骤4：Archive集粒子筛选。当候选解加入至Archive集之后，可能会导致Archive集规模比N′大，由此要对Archive集中的粒子进行筛选：针对网格 Gk′，假设D'k′＞1，那么依据下式对粒子进行筛选。

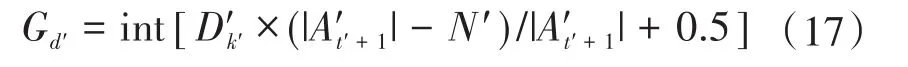
式中：Gd′为 Gk′要淘汰的粒子数量；|A't′+1|为 Archive集添加候选解之后的规模。

当确定Gd′之后，依据下式对Gk′中粒子和理论Pareto前端之间的距离进行计算[20-21]，同时将距离Pareto前端比较远的粒子依次淘汰掉。

式中：D'Gk′,i为 Gk′中粒子和理论 Pareto前端之间的最短距离；P'Gk′,i为 Gk′的 Pareto 前端；P'T′,j为 T′的Pareto前端。

1.3.2 自适应混沌优化

部分理论Pareto最优解并没有在Archive集中进行存储，则之后再找Pareto最优解将会非常难。引入自适应的混沌优化方法，整体思路为：随机选取Archive集中的一部分粒子实行混沌优化，假设粒子i在整个混沌优化过程中的第k′-1，k′，k′+1 代位置为 C'k′-1,i，C'k′,i，C'k′+1,i，P'k′-1,i，P'k′,i，P'k′+1,i代表 C'k′-1,i，C'k′,i，C'k′+1,i的 Pareto前端，那么第 k′-1，k′，k′+1代间 Pareto前端距离D'k′,k′-1，D'k′,k′+1可表示为

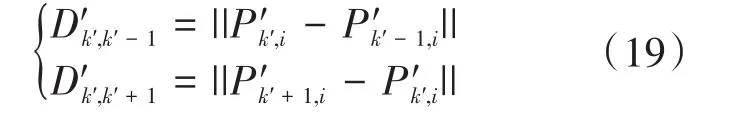
假 设 混 沌 迭 代 控 制 阈 值 diffD′是 D'k′,k′-1和D'k′,k′+1的差值，即

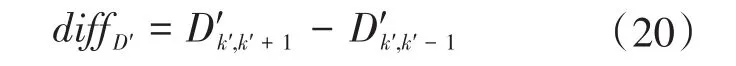
当diffD′＞0，则代表算法处在进化的状态，能够减少总迭代次数，进而提升算法运行效率；当diffD′＜0，则代表进化性能比较低，要增加迭代次数。混沌优化迭代的数量自适应方案可表示为

1.3.3 Pareto最优解选取

混沌蛙群算法基于网格粒子的密度值，在Archive集合中给每只青蛙选取1个Pareto最优解实行更新操作。针对 Gk′，假设 D'k′＞0，那么其网格的适应度值 f′(Gk′)能够表示为 D'k′的倒数，则有：

混沌蛙群算法基于网格 f′(Gk′)，通过轮盘赌方式给蛙群中的每只青蛙选取一个网格，同时从网格中任意选取1个个体当作最优解并进行更新。所得Pareto最优解选取方案使Archive集合中D'k′越小的网格当选的概率就越大，以此保障Pareto最优解具备多样性。

2 实验结果与分析

为验证基于混沌蛙跳算法的综合能源系统中多能源协同优化方法有效性，进行一次相关性测试。实验对象选择在某市的某工业园区中综合能源系统的一个示范性工程试点，园区内部一共设置了15个下层用户工厂与1个上层具有综合性的能源提供商。基本数据为：燃气轮机2台，风电机组4台，光伏机组2台，太阳能热水锅炉5台，吸收式的制冷机3台，电制冷机2台。将测试所得数据传输至Matlab软件中进行模拟，主要为风电机组发电功率、储能等机组约束物理量。

根据电量均衡性要求，供电可靠程度设计一个下限值，其必须不大于负荷，也就是说可靠性约束目标实行优化中，需要以电负荷来作为衡量指标。经过测试得到的原始电负荷与优化之后的电负荷差别如图3所示。

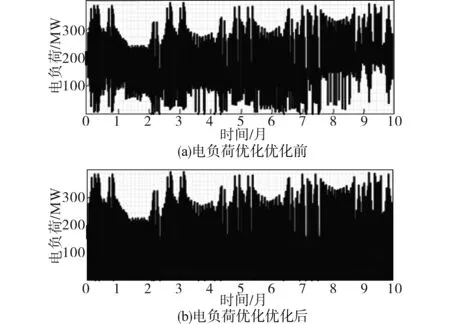
图3 电负荷优化前后对比Fig.3 Comparison before and after electric load optimization

分析图3可知，电负荷在优化前、后有显著改变。与优化之后的电负荷相比，原始负荷有明显降低趋势，电负荷的均衡性更强，在不同实验次数下，系统的减排率均在20%以上，表现出了良好的减排性能。

混沌蛙跳算法每次进化会生成新Pareto最优解粒子，然而，假设部分理论Pareto最优解并没有在Archive集中进行存储时，那么，对Archive集中的粒子进行筛选时，为了匹配Pareto最优解就需要引入自适应的混沌优化方法。而设备燃料消耗和定期维护成本费用是生产运行维护成本费用的主要来源，其中，清洁机组补偿费需要根据不同时段的机电组调整过度调度情况和欠调度情况，在这个过程中的优化模型参数需要自适应，以符合时段要求，因此进行自适应能力的测试。将本文方法与文献[4]～文献[6]的自适应能力对比，对比结果如图4所示。

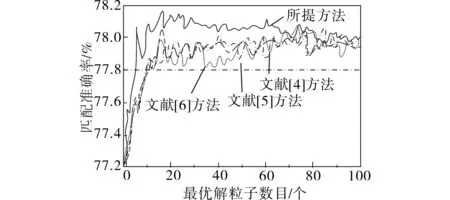
图4 各个方法自适应能力对比结果Fig.4 Comparison results of adaptive ability of each method

由图4可知，假设有100个最优解粒子没有被集中储存，则这100个粒子将会被自适应优化，在本文方法与文献[4]～文献[6]的自适应能力对比结果中，各个方法的自适应准确率皆随粒子数目的增多而不同程度地波动，其中波动最小的曲线为本文方法测试所得曲线，说明本文方法自适应准确率最高，可以根据不同时段的机电组调整过度调度情况和欠调度情况，实现机电组的能耗和成本控制，其协同优化方案的可靠性得到证明。

基于混沌蛙跳算法的综合能源系统中多能源协同优化方法中提出的目标模型中包含了最优解选取等指标，且约束条件与目标函数也具有相符合的特性，在混沌蛙跳算法运行中，引入了子群划分方案，网格密度机制可以在一定程度上调整集粒子均匀性，以下进行本文方法与文献[4]～文献[6]方法的网格密度机制测试，测试结果如图5所示。

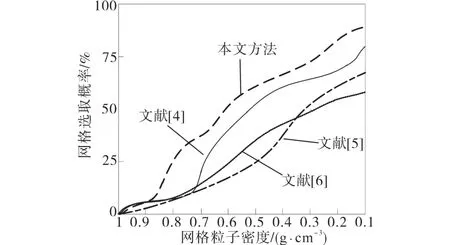
图5 各个方法网格密度机制测试结果Fig.5 Grid density mechanism test results of each method

Pareto最优解选取方案使Archive集合中D'k′越小的网格当选的概率就越大，能够解决多目标优化问题。由图5可知，本文方法通过自适应混沌法选取的网格密度对最优解集合多样性进行了优化，使得到的多能源协同优化方案更加贴合实际需求，提高了所提方法的可靠性。

3 结论

面向多能源协同优化，提出基于混沌蛙跳算法的综合能源系统中多能源协同优化方法。以总费用最低和系统可靠性最强等为目标函数，引入混沌蛙跳算法对目标函数进行求解，得到多能源协同优化最佳方案。经测试，与传统方法相比，本文所提出的方法可有效解决能源负荷和系统减排等问题，可靠性很强，对成本和能耗的控制能力较高，但是要在控制之前根据系统动态模型分析系统运行状态呈现出的动态特征，因此未来研究中应考虑该方法的简便算法，为该领域的相关研究提供实际参考价值。