基于BP神经网络汽水分离器组合建模研究

康宁，张仁义，胡庆军，王庭宽，赵博

（天津电气科学研究院有限公司，天津 300180）

随着我国超临界机组的发电技术的发展，对于机组运行人员的水平要求越来越高。为了准确反映出超临界机组设备参数和动态机组响应过程的变化，建立数学模型是最有效的研究方法。因此，能够建立正确的超临界机组数学模型，对于研究其控制策略、提高运行人员的水平有着极为关键的作用。

文献[1]建立了直流炉的非线性简化模型，并对开环阶跃扰动实验和现场数据进行了比对，结果表明，模型具有一定精度，可以用来设计协调控制系统控制器。文献[2]采用集总参数法对机炉进行建模，并在仿真模型上进行阶跃扰动实验，仿真结果和实际机组动态特性基本一致。文献[3]通过模块化的方式，建立了汽水分离器的动态数学模型，在热力系统仿真上具有一定的参考价值。

本文以汽水分离器的建模过程为例，阐述了以机理建模和神经网络建模相结合的组合建模方法，本文的建模方法也适用于其他热力系统。

1 汽水分离器数学模型

汽水分离器的动态特性极其重要，在超临界机组的启动系统中，会影响整个系统的性能。汽水分离器在低负荷下的作用是分离蒸汽和水；在高负荷的情况下，它将会切换到直流运行，并且汽水分离器类似于联箱[4]。

在对汽水分离器建模之前，先进行以下简化的假设：汽水分离器金属温度等于工质温度，而且与工质温度同步；汽水分离器是圆柱形的[5]。

图1为汽水分离器物理模型示意图。本文建立的汽水分离器数学模型如下文所述。

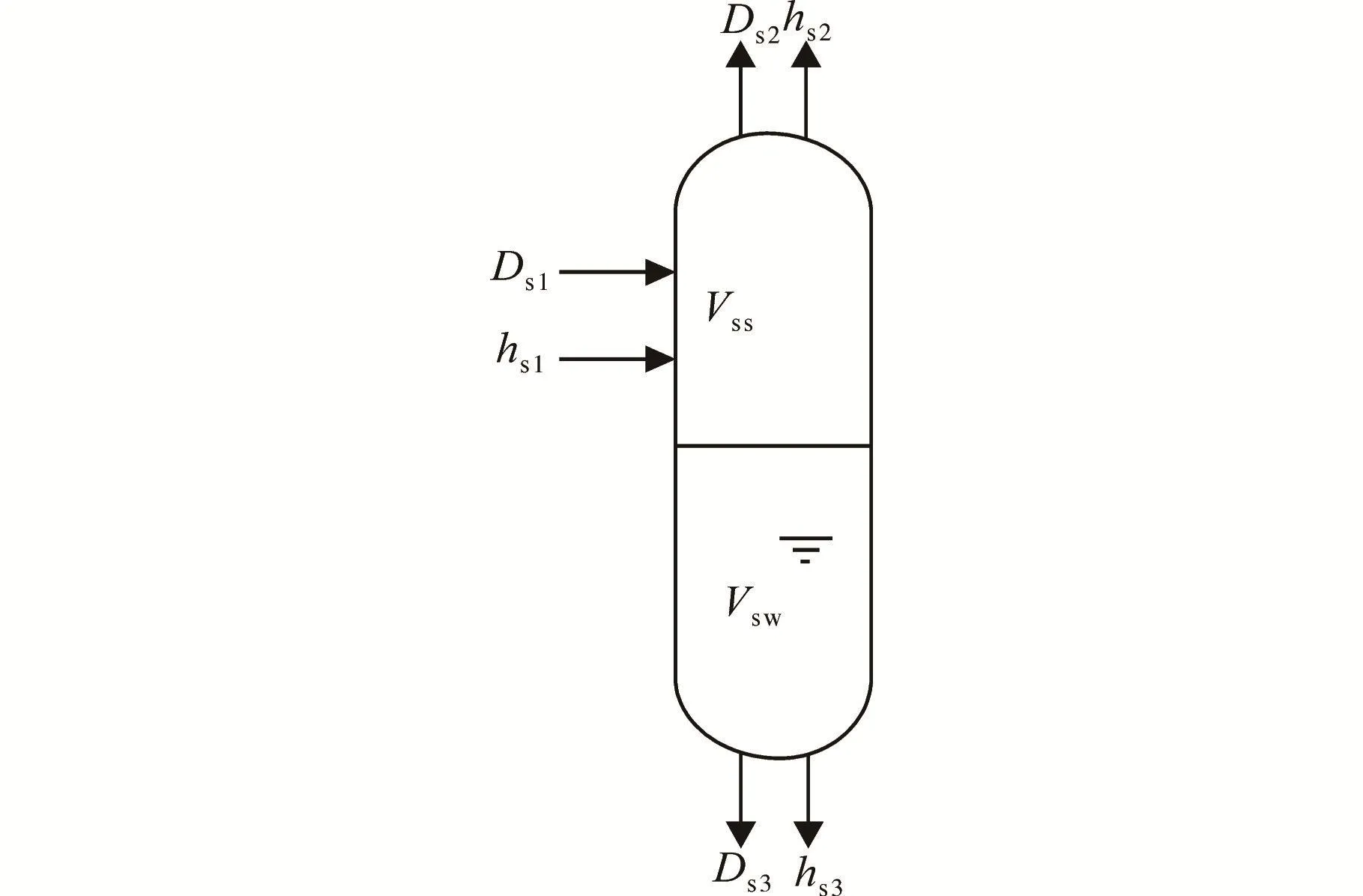
图1 汽水分离器物理模型示意图Fig.1 Schematic diagram of the physical model of the steam-water separator

1.1 汽水分离器质量守恒方程

汽水分离器质量守恒方程如下：

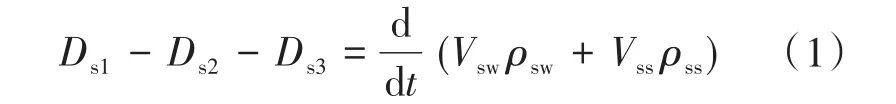
式中：Ds1为用于进入汽水分离器流量；Ds2为排汽流量；Ds3为排水流量；ρsw为水的密度；ρss为汽的密度；Vss为汽空间容积；Vsw为水空间容积。

1.2 汽水分离器能量守恒方程

汽水分离器能量守恒方程如下：

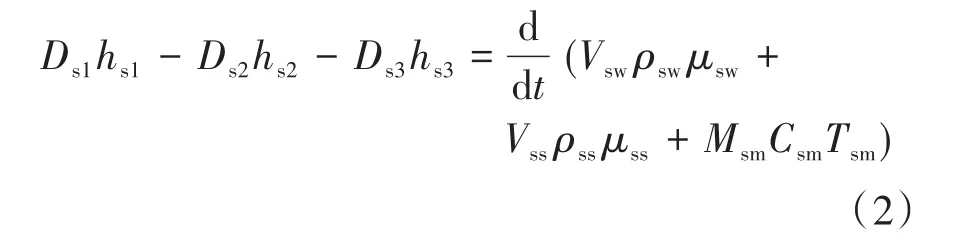
式中：hs1为汽水分离器入口焓值；hs2为排汽焓值；hs3为排水焓值；μsw为水的内能；μss为汽的内能；Msm为有效金属质量；Csm为有效金属比热；Tsm为有效金属温度[6]。

1.3 汽水分离器压力

1）当锅炉在湿态运行时，其内部压力较低[7]，此时，汽水分离器压力可以用下式来计算：

1.4 汽水分离器产汽量

汽水分离器入口阀门前后的焓值相等，则进入汽水分离器的干度为

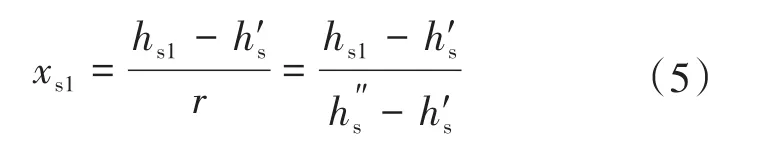
式中：xs1为汽水分离器入口干度；r为汽化潜热；h's为压力下的饱和水焓；为压力下的饱和汽焓。当xs1≤0时，表示为未饱和水状态；当0＜xs1＜1时，表示为饱和状态；当xs1≥1时，表示为过热蒸汽状态[8]。

1）当进入汽水分离器的温度高于在一定压力下的饱和温度，会产生蒸汽，即当进入汽水分离器的干度0＜xs1＜1时，则产汽量Ds1s为[9]

2）当进入汽水分离器的干度xs1≥1时，其产汽量为

1.5 汽水分离器水位

1）当0＜xs1＜1时，由式（6）可知进入汽水分离器水量为

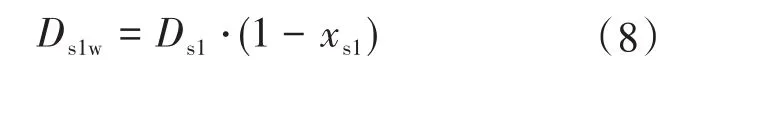
式中：vsw为汽水分离器中水的比容；rs为汽水分离器内半径[10]。

1.6 汽水分离器内工质干度

由湿饱和蒸汽干度的定义，可以看出其干度为

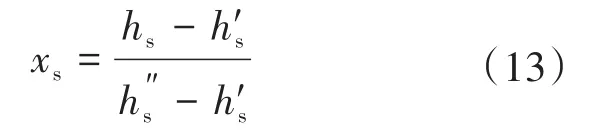
1.7 汽水分离器内工质比焓

根据汽水分离器能量守恒方程，即式（2）以及式（4），可以得到：

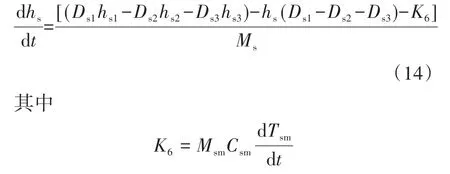
2 神经网络权值调整算法

前向神经网络的逼近效果在非线性系统中应用很广泛，它对辨识稳态和动态的非线性系统有很强的作用，是颇有成效的神经网络之一[9]。在训练过程中，该网络采用的是误差反向传播（back-propagation）算法，也叫BP神经网络。BP神经网络是由3部分组成的，包括输入层、中间层和隐藏层，每个相邻层之间都由神经元连接，但是每层中的每个神经元是独立的。现有的BP神经网络算法可以用来调整神经网络的权值。其中机理模型的结构是确定的，并且由神经网络来计算中间系数。在训练神经网络过程中，神经网络的输入可被作为机理模型的输出，由此神经网络的期望输出能被计算出，最后，通过比较神经网络的实际输出与期望输出，可以获得神经网络的输出误差[11]。

图2为典型的3层BP网络结构图。

图2 BP网络结构示意图Fig.2 BP network structure diagram

研究对象中所需要的输入和输出数量能决定神经网络的输入层和输出层中的神经元数量。可以通过建模过程中确定隐藏层神经元个数来获得最合适的隐藏层神经元个数[12]。

神经网络输入量确定原则：影响汽水分离器参数分布的重要因素（例如进入汽水分离器的蒸汽流量、干度、焓值、主汽压力等）都可以看作神经网络的输入量。神经网络的输出数量取决于机理模型中需要识别参数的个数，汽水分离器需要辨识的参数为蒸发系数和水传热系数，则所建立神经网络的输出是蒸发系数和水传热系数[13]。

汽水分离器组合模型结构如图3所示。

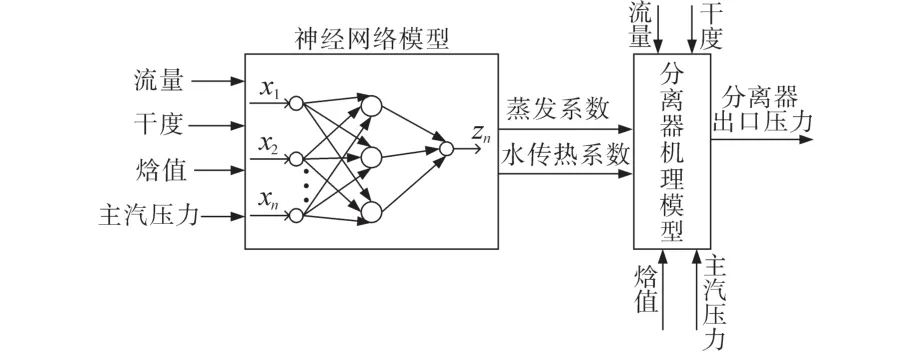
图3 汽水分离器组合模型结构Fig.3 Steam-water separator combined model structure

3 应用

根据上述组合建模方法，对某台容量为1 000 MW电厂的汽水分离器进行建模，首先利用机理建模法来确定模型的结构，然后用神经网络来确定模型的系数。为了提高模型的精度，可以对神经网络进行训练，得到一个相对固定的神经网络，进而输入变量的变化会影响机理模型中系数的变化[14]。

用于训练的2 000组数据从电厂SIS系统中采集，在训练过程中，要想使整个网络处于最佳结构，应调整输入输出的个数和隐藏层神经元的数量。经过实验，神经网络的最终结构如下：流量、干度、焓值和主汽压力作为神经网络输入量，隐藏层神经元个数4个，输出层神经元个数2个。

把2 000组现场数据输入到将机理模型和神经网络相结合的组合模型中，组合模型的汽水分离器压力测试效果图如图4所示，其中，采样周期为10 s。

由图4可知，模型输出蒸汽压力的变化趋势接近现场实际运行数据变化的基本趋势。汽水分离器压力测试残差如图5所示。从图5中可以看出，误差较小，采用组合建模方法所建立的汽水分离器模型能够很好地反映汽水分离器出口压力的变化情况，模型精度较高而且可靠性强。

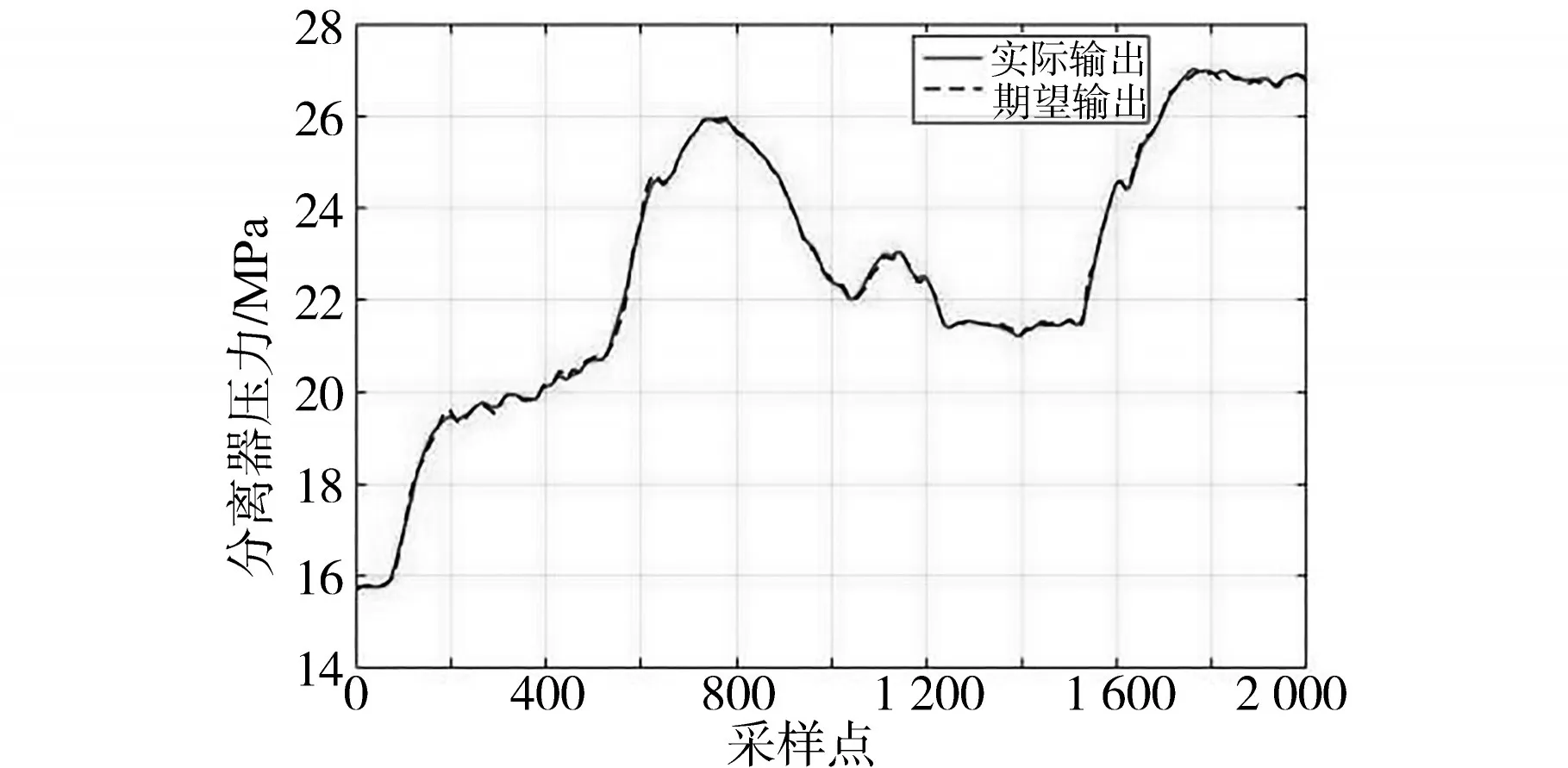
图4 汽水分离器压力测试效果Fig.4 Pressure test effect of steam-water separator

图5 汽水分离器压力测试残差Fig.5 Steam-water separator pressure test residuals

4 结论

本文分析了集总参数法建模和试验建模的不足，并以汽水分离器为例，提出了一种以机理模型和神经网络相结合的组合建模方法，目的是建立一个能够准确反映汽水分离器动态特性的组合模型[15]。其中，以机理模型为主要模型，用神经网络模型来计算机理模型中的未知系数，并且神经网络机理模型的权值需根据其输出值偏差来调整，该组合建模的方法提高了神经网络模型的适用性及精准度。通过在仿真平台开发的神经网络和机理模型，封装在模型库中，可应用于实际工程中。综上所述，通过组合建模所获得的仿真模型具有较好的通用性，在火电机组仿真中应用前景值得期待。