图卷积网络与自注意机制在文本分类任务上的对比分析
2022-01-20蒋浩泉张儒清郭嘉丰范意兴程学旗
蒋浩泉,张儒清,郭嘉丰,范意兴,程学旗
(1. 中国科学院 计算技术研究所 网络数据科学与技术重点实验室,北京 100190;2. 中国科学院大学,北京 100049)
0 引言
表示学习(RepresentationLearning)对于分类、匹配、生成等任务都至关重要,传统特征表征工程需要人工设计特征。但深度学习可利用神经网络技术根据设定的任务目标自动学习得到输入及中间环节良好的分布式向量表示。多层感知机(Multi-Layer Perceptron,MLP)、卷积神经网络(Convolutional Neural Networks,CNN)[2-3]和循环神经网络(Recurrent Neural Networks,RNN)[4]是此前最常用的神经网络结构,被广泛用于自然语言处理、计算机视觉、语音识别等领域文本、图像及语音等信息的表示。
随着深度学习研究的发展,近期图卷积网络(Graph Convolutional Networks,GCN)和自注意(self-attention)机制获得了机器学习从业者们的大量关注。作为深度学习领域的最新进展,两者近期众多相关研究成果纷纷涌现。
目前最常采用的图卷积网络形式作为谱图卷积的局部一阶近似被提出,是一种简单而有效的图神经网络(Graph Neural Networks,GNN)。相比传统神经网络只能用于一般如文本序列、图像栅格等的网格状数据,图神经网络能够对非欧氏度量空间的数据进行建模。图卷积网络是传统神经网络中卷积神经网络结构在图数据上的推广,它本质是一种可直接作用于图上的多层神经网络。图卷积网络基于每个节点的邻居节点生成该节点的嵌入向量表示,该嵌入表示能将局部的图结构以及临近节点的特征信息编码入其中。图卷积网络通过一层卷积操作只能获取到其直接邻居节点的信息,而通过多层图卷积网络堆叠,就能整合更大范围的临近信息。
自注意机制是一种特殊的注意力(attention)机制。注意力机制现已成为神经网络领域最重要的概念之一,它使得神经网络模型能够根据自身需求灵活自动地关注输入数据或特征中重要的部分,极大地提高模型的表达能力。注意力机制最初是与编码器-解码器(encoder-decoder)架构相结合而被用于机器翻译领域[5],其要求输入与输出都是一个序列。但是对于诸如文本分类等任务,其输入是一个序列,而输出并不是序列的形式,故自注意机制的思想被提出,直接在一个序列内部实现注意力机制的运用。此后,Transformer架构[6]横空出世,为自然语言处理领域预训练模型[7]研究的热潮奠定了基础,而这些模型的共同核心思想之一就是自注意机制。
在将图卷积网络与自注意机制在工作原理上进行对比分析后,我们发现两者在形式上极其相似。一次图卷积操作和一次自注意步骤之间的区别仅在于对表示节点间连接关系的邻接矩阵的计算方式不同。从某种角度上可以认为,自注意机制也以其所有输入样本为节点,构建了一个全连接的图。并且,图卷积网络中用于表示节点间关系的邻接矩阵往往是训练之前人为预先给定的,而自注意机制中与之相对应表示节点之间连接关系的矩阵则是由可学习的参数根据不同任务特性学习得到的,即各节点之间连边的权重甚至图的结构(连边权重为0则代表无连接,否则代表有连接)都是由可学习的参数根据不同任务的学习目标自适应地决定的。因此,自注意机制在某种程度上可以说是图卷积网络的一种泛化,具有较图卷积网络更强的表达能力。我们进一步推测,相比图卷积网络,在实际任务中使用更具表达能力的自注意机制将可能带来性能上的提升。
为了在实际任务中验证上述想法,我们选择了自然语言处理最基本问题之一——文本分类任务,将其作为代表进行对比实验。最终的实验结果显示,在相对对等的条件下,采用自注意机制的模型在多个文本分类数据集上的表现都显著优于使用图卷积网络的对照模型,甚至超过了目前图卷积网络用于文本分类任务的最先进水平。除此之外,我们还观察到,随着数据规模的增加,使用自注意机制的模型和使用图卷积网络模型之间的性能差距也逐渐扩大。这些结果从实际任务表现方面,验证了自注意机制确实具有较图卷积网络更强表达能力的观点。
需要指出的是,虽然本文对图卷积网络和自注意机制之间关系的理论分析,以及随后在文本分类任务上的实验验证等部分,对其他任务或领域可能也具有一定的启发作用,但是本文的目标和讨论范围实际上是紧密限制在文本分类任务以及模型的文本分类效果上的。对于其他任务和领域,以及性能表现和更深层的数学原理等其他课题,则是已经超出了本文的研究范围。对于这些研究课题,我们将在本文最后进行一些抛砖引玉式的列举,并作为后续工作考虑的一个研究方向。
本文第1节简要介绍图卷积网络和自注意机制的一些相关工作;第2节对比图卷积网络与自注意机制的工作原理,证明后者在某种程度上可被视为前者的一种泛化;第3节通过文本分类任务对比实验的实际表现,验证自注意机制较图卷积网络具有更强的表达能力,可获得更佳性能。最后,对本文进行总结,并提供一些未来可能进行的工作和研究方向。
1 相关工作
本节将简要介绍一些图卷积网络和自注意机制的主要相关工作。
1.1 图卷积网络
深度学习能有效捕获欧氏度量空间下数据的潜在模式,然而如今越来越多的数据则是通过图的形式表示。例如,电子商务中顾客与商品间的交互关系、生物化学中分子与药物构成的网络,以及引文网络中文献之间的引用关系等。图的不规则性使得一些如卷积等重要的操作在图像域可以很容易计算,但却难以直接运用到图数据上。此外,现有机器学习算法的一大重要前提假设就是样本之间相互独立。而这在图数据上显然是不成立的,因为代表样本的节点之间都通过边相互关联在一起[8]。
近年来,研究者们将传统神经网络中的如卷积神经网络结构进行了拓展推广,重新定义了在图数据上的卷积操作。类似在图像上的卷积操作,图上的卷积可以定义为取节点所有邻近信息的加权平均。第一项在谱图卷积网络领域的先驱工作是由Bruna等人[9]进行的,他们基于谱图理论定义了一个图卷积的概念。此后,又有众多工作对谱图卷积网络进行了改进、拓展和近似[10-12]。这些工作中,Kipf等人[12]提出了一个谱图卷积的局部一阶近似版本的图神经网络,即图卷积网络,在多个标准图数据集上实现了当时最好的分类结果。此外,Marcheggiani等人[13]为了使图卷积网络能够处理更复杂的,如包含语法等信息的图结构等,他们为图卷积网络引入了处理连边方向和标签种类的新机制。
图卷积网络也被应用于多个自然语言处理任务上,例如,文本分类[14-15]、机器翻译[16-17]、摘要生成[18]、阅读理解和问答[19]等。有关图卷积网络、图神经网络更全面的介绍可以参考Zhang等人[20]和Wu等人[8]的综述文献。
1.2 自注意机制
注意力机制最初是与编码器-解码器(encoder-decoder)架构相结合被用于机器翻译领域[5]的,使得模型能够根据自身需求灵活地自动关注输入数据中重要的部分。但是对于诸如文本分类、推荐等任务,其输入是一个序列而输出并不是序列的形式,故Yang等人[21]提出了自注意机制,用于直接在序列内部实现注意机制的运用。
此后,Transformer架构[6]横空出世,为自然语言处理领域预训练模型[7]研究的热潮奠定了基础,而这些模型的共同核心思想之一就是自注意机制。每一层的自注意机制将同一输入序列中各字符的特征表示向量相互关联起来,用序列中所有位置的向量表示经过映射变换后的加权平均来作为每个位置新的向量表示。Transformer架构还引入了多头(multi-head)自注意机制的概念,将多个自注意模块并行而不是前后按顺序地堆叠在一起,并在之后进行汇总。不同的并行自注意模块输入数据相同,有助于捕获输入数据中不同层面的特征信息,提高了模型的表达能力。
除被用于众多预训练模型外,不同形式的自注意机制的思想也被运用于推荐系统[22]、自然语言理解[23]及对句子的表示学习[24]。自注意机制是一种特殊的注意力机制,而注意力机制现已成为神经网络领域的一个重要概念。关于其更全面的介绍,可以参考Chaudhari等人[25]的综述文献。
1.3 图卷积网络与自注意机制
注意力机制已被广泛运用于基于序列的任务中,它最大的优点就是使得神经网络模型能够根据自身需求灵活自动地关注输入数据或特征中重要的部分,极大提高了模型的表达能力。众多研究开始尝试将注意力机制融入各种神经网络模型中去,图神经网络也不例外。
Velickovic等人[26]在聚合临近节点特征信息时使用注意力机制确定各节点的权重,并且融入了多头注意力机制提出了图注意力网络(Graph Attention Networks,GAT)。Zhang等人[27]提出的门控注意网络(Gated Attention Network,GAAN)进一步引入了自注意机制,用于计算不同注意力头部的权重而非直接加和平均。对于注意力机制在图上运用的更全面介绍,可参考Lee等人[28]的综述文献。
然而据我们所知,现有的已正式发表的文献中,尚未对图卷积网络与自注意机制之间的关系进行分析和讨论。
2 模型分析
本节将对比分析图卷积网络与自注意机制的工作原理,证明后者在某种程度上可被视为前者的一种泛化,继而推断自注意机制具有较图卷积网络更强的表达能力。
2.1 图卷积网络
目前,普遍被采用的图卷积网络形式是由Kipf等人[12]作为谱图卷积的局部一阶近似提出的,是一种简单而有效的图神经网络。图卷积网络本质是一种可直接作用于图上的多层神经网络,它基于每个节点的邻居节点生成该节点的嵌入向量表示,该嵌入表示能将局部的图结构以及临近节点的特征信息编码入其中。
考虑包含n个节点的图G,每个节点都有一条自连边。图G的邻接矩阵为A,由于自连边,其对角线上的元素全为1。度矩阵D计算如式(1)所示。
Dii=∑jAij
(1)
令X∈Rn×m为包含所有节点特征的矩阵,m为特征表示向量的维度。
图卷积网络通过一层卷积操作只能获取到其直接邻居节点的信息,而通过多层图卷积网络堆叠,就能整合更大范围的临近信息。对一层图卷积网络来说,新的节点特征矩阵H(l+1)∈Rn×k通过式(2)得到:
(2)
通常还要通过激活函数σ,即H(l+1):=σ(H(l+1))。其中,W(l)∈Rm×k是对特征矩阵H(l)进行线性变换的参数矩阵;l代表层数,网络的输入特征矩阵即为初始节点特征矩阵,如式(3)所示。
H(0)=X
(3)

(4)

此外,Marcheggiani等[13]为了使图卷积网络能够处理更复杂的,如包含语法等信息的图结构,他们为图卷积网络引入了处理连边方向和标签种类的新机制。在他们经过拓展后的图卷积网络中,一个新节点v的特征表示向量表示如式(5)所示。
(5)
其中,N(v)代表节点v的邻居节点集合;W(l)和b(l)代表可学习的参数矩阵或参数;L(u,v)是返回两节点u和v之间连边方向和类型的函数。相对式(2)中的W(l),不同方向和不同类型的连边在这里由不同的可学习参数表示。同样,最后将所有邻居节点变换后的表示被聚合起来,得到该节点新的特征表示向量。
引入处理连边方向和标签种类机制的图卷积网络的工作原理可大致由图1的左半部分示意。由于不同指向、不同类型的连边,其节点变换参数矩阵也不相同,所以总的图卷积网络可按照不同方向、不同类型边拆分成多个子图分别进行图卷积,最后再将所有子图相加得到最终新的节点表示。为了简化表示,这里忽略了边的方向,只按照边的类型对图卷积网络进行了分解。
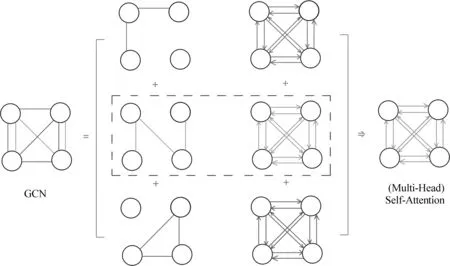
图1 图卷积网络(左)与(多头)自注意机制(右)的对比示意图
2.2 自注意机制
现被广泛使用的自注意机制见于由Vaswani等人[6]提出的Transformer结构中,最早用于机器翻译。自注意机制是一种特殊的注意力机制,相对初始的注意力机制[5]更擅长捕捉数据特征内部的相关性,减少了对其他外部信息的需求依赖。它使得神经网络模型能够根据自身需求灵活、自动地关注输入数据或特征中重要的部分,极大地提高了模型的表达能力。
为了简化且不失一般性,我们略去层数标识,并如同Transformer编码器部分,自注意力机制包含三个特征矩阵Query、Key、Value(下文分别用Q、K、V表示),且三个矩阵相同,,用H∈Rn×dmodel表示。自注意机制可表示如式(6)、式(7)所示。
其中,参数矩阵WQ∈Rdmodel×dk、WK∈Rdmodel×dk、WV∈Rdmodel×dv;softmax是对矩阵按行进行softmax归一化。实际上,按行softmax归一化可以分解为先对矩阵逐元素求指数的exp运算,再按行进行归一化。令
(8)

(9)
作为自注意机制的一种泛化,多头自注意机制将多个自注意模块并行而不是前后按顺序地堆叠在一起,并在之后进行汇总。不同的并行自注意模块输入数据相同,有助于捕获输入数据中不同层面的特征信息,提高了模型的表达能力。多头自注意力机制的计算如式(10)所示。
Multi-Head(H)=Cat(SA1,…,SAh)WO
(10)
其中SA是自注意机制的简写,表示多个并行的自注意模块;Cat是矩阵的拼接操作;h为自注意头的数目;多个自注意力头拼接后,再与WO∈R(h×dv×dmodel)参数矩阵进行计算,如式(11)所示。
SAi=Self-Attentioni(H)
(11)
实际上,将多个向量或矩阵拼接后再利用矩阵相乘进行线性变换,在最终数值计算得到的结果上等价于分别进行矩阵相乘线性变换后再相加,如式(12)所示。即就计算结果而言,式(10)可与式(12)等价。
Multi-Head(H)=SA1W1+…+SAhWh
(12)
2.3 图卷积网络和自注意机制的对比

首先,从对原始邻接矩阵的归一化方式上看,图卷积网络与自注意机制存在细微差异,这也导致了两者所构建图连边的类型不同。通过表示两者对原始邻接矩阵的归一化的式(4)和式(9)可以看出,图卷积网络采用的是对称归一化,而自注意机制采用的则是行归一化。因此,图卷积网络所构建的是一个无向图,而自注意机制构建的则是一个有向图。
其次,相比图卷积网络中原始邻接矩阵A往往是训练之前人为预先给定的,自注意机制中与之相对应表示节点之间连接关系的矩阵是由可学习的参数根据不同任务特性学习得到,即各节点之间连边的权重甚至图的结构(连边权重为0则代表无连接,否则代表有连接)都是由可学习的参数根据不同任务的学习目标自适应地决定的。
通过图1中央虚线方框部分可清晰地看到单层图卷积网络与单头注意力机制之间的关系。左侧的图卷积网络构建了一个无向图,且节点之间的连接关系及权重是人为预先给定的。而自注意机制则是构建了一个有向全连接图,其各节点之间连边的权重甚至图的结构都是由可学习的参数根据不同任务的学习目标自适应地决定的。图中只表示了结构,没有表示边的相对权重大小。
即使是对于引入处理连边方向和标签种类机制的图卷积网络,通过图1我们也可以直观地看到,多头自注意机制也能通过多个并行的自注意模块以及可学习的参数对图卷积网络进行表达。实际上,每个自注意头并不一定如图中所示那样是一一对应的。因为相比于左侧图卷积网络中边的类型需要提前定义,自注意机制则可以根据不同任务目标、通过可学习的参数自动学习捕获到模型各部分的良好表示,而这并不一定与前者预先定义的一致。
试想在极端的情况下,如果完全符合任务的目标,那么自注意机制中的矩阵A也可通过可学习参数的改变表示为与图卷积网络中邻接矩阵A数值相等。由此可以看出,可学习参数的引入,使得自注意机制较图卷积网络具有更强的模型表达能力。换而言之,在某种程度上,我们可以说自注意机制实际上是图卷积网络的一种泛化。
3 实验设计与分析
本节在文本分类任务上,对分别使用图卷积网络和自注意机制的模型进行实验。具体来说,在从原理上分析得到自注意机制可看作是图卷积网络的一种泛化形式后,从实际任务表现方面验证: 是否使用自注意机制的模型确实具有较图卷积网络更强的表达能力,从而性能更佳。
3.1 模型设计
首先,我们与多个图卷积网络相关的文本分类基准模型进行比较,主要包括:
•Text-GCN: Yao等[14]将图卷积网络应用于文本分类任务,提出了Text GCN模型。该模型为整个数据集构建一张图,以整个数据集的所有词和句子作为节点,基于词的共现信息和文档-词的关系(点互信息PMI和TF-IDF)设计连边权重。模型采用堆叠的两层图卷积网络,其中,节点被初始化为词和文档的独热向量,即X=I,且训练过程中该输入层参数固定。
•Conv-GNN: Huang等[15]认为,以往的图神经网络往往是在整个数据集上构建一个大图。这导致极高的内存消耗,以及无法对新来的数据进行在线测试,因为新数据并不包含在已经构建好的图中。为此,他们为每个输入文本构建图,连边权重由可学习的参数决定,且各参数共享以保留全局信息。虽采用的不是图卷积网络的形式,但也是一种卷积图神经网络。其中,节点采用GloVe向量[29]初始化。
•Text-GCN*: 为了与实验组进行公平的对比,消除引入GloVe向量可能带来的影响差异,我们也用GloVe向量初始化Text-GCN的节点特征,并且在训练过程中节点向量的参数是可变的。若无特别说明,本文中特征表示向量都采用GloVe向量初始化,且都是在训练过程中可变的。
为了对图卷积网络和自注意机制进行较为公平的对比,我们设计了如下实验组:
•GCN: 采用Conv-GNN的做法,该模型以每个输入文本的所有词和该文本作为节点构图,再用两层的图卷积网络对该文本进行类别预测,词节点向量表示全局参数共享。图的邻接矩阵即节点之间的连边权重计算方式则与Text GCN相同,由点互信息PMI和TF-IDF所确定,计算如式(13)所示。
其中,Aij表示节点i和节点j的连边权重。
•SA: 输入与GCN相同,以单个文本为单位,可视为所构图节点相同。但模型是两层先后次序堆叠的自注意机制,因此节点之间连边权重完全是由可学习参数决定的。
3.2 数据集与评价方法
我们在三个被广泛使用的文本分类数据集上进行了对比实验,即R8、R52(1)https://www.cs.umb.edu/smimarog/textmining/datasets/,以及Ohsumed(2)http://disi.unitn.it/moschitti/corpora.htm。
• R8和R52都是Reuters 21 578数据集的两个子集,分别包含8种和52种类别标签。
• Ohsumed来自于多标签分类数据集MEDLINE,然而我们仅关注单标签分类,因此含有多个标签的样本没有包含在最终的数据集中。
表1展示了所采用数据集的部分统计数据,包括训练集和测试集的样本数、所构成图的总节点数,以及所含类别数目。

表1 数据集的统计信息
此外,我们采用了与Text GCN[14]工作相同的模型评价指标,即通用的分类准确率。其计算方式为类别预测正确的样本占总待预测样本的比例。
3.3 实验设置
对于Text-GCN、Conv-GNN和Text-GCN*这三个对照模型,其参数及训练过程可参考其原论文[14-15]。
对GCN和SA两个实验模型,我们使用Adam优化器[30],初始学习率为0.001。Dropout概率为0.5,L2正则化权重为0。其他预处理方法、数据集划分方式以及参数设置均与Text GCN[14]相同。
3.4 实验结果与分析
表2展示了各模型在各文本分类数据集上的分类准确率,都是运行多次取均值和标准差后的结果,部分数据来自于Yao等人[14]和Huang等人[15]。
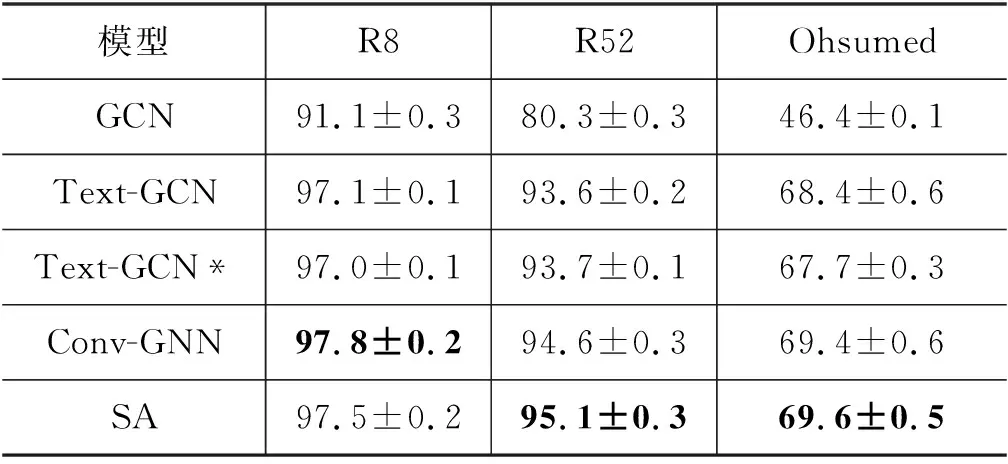
表2 模型在测试集上的准确率
对比代表图卷积网络的GCN模型和代表自注意机制的SA模型的分类准确率我们可以看到,使用自注意机制的模型在多个文本分类数据集上的表现都明显超越了使用图卷积网络的模型,且存在较大差距。GCN模型相对SA模型的区别仅在于: GCN模型的邻接矩阵计算方式即节点间的连接关系及权重是提前根据经验人为设计并固定的,而SA模型由于采用的是自注意机制,相对应地表示节点之间连接关系的矩阵则是由可学习的参数根据不同任务特性学习得到,即各节点之间连边的权重甚至图的结构都是由可学习的参数根据不同任务的学习目标自适应地决定的。该现象表明,可学习参数的引入,使得自注意机制较图卷积网络具有更强的模型表达能力。
继续观察GCN和SA这两组实验,我们发现随着数据集规模的增大,两模型的性能差距也相应扩大,如图2所示。横轴依次代表的是R8、R52以及Ohsumed数据集构图所含的节点总数依次增大,纵轴表示分类准确率,图中深色部分即表示了使用自注意机制的SA模型与使用图卷积网络的GCN模型之间的分类准确率差异。可以直观地看到,随着代表数据集规模的构图节点数目的增加,深色部分的纵向距离不断增大。这说明,随着数据规模的增加,更具表达泛化能力的自注意机制能够更好地捕获并表示数据中与任务目标一致的特征,从而取得较图卷积网络更优异的性能表现。
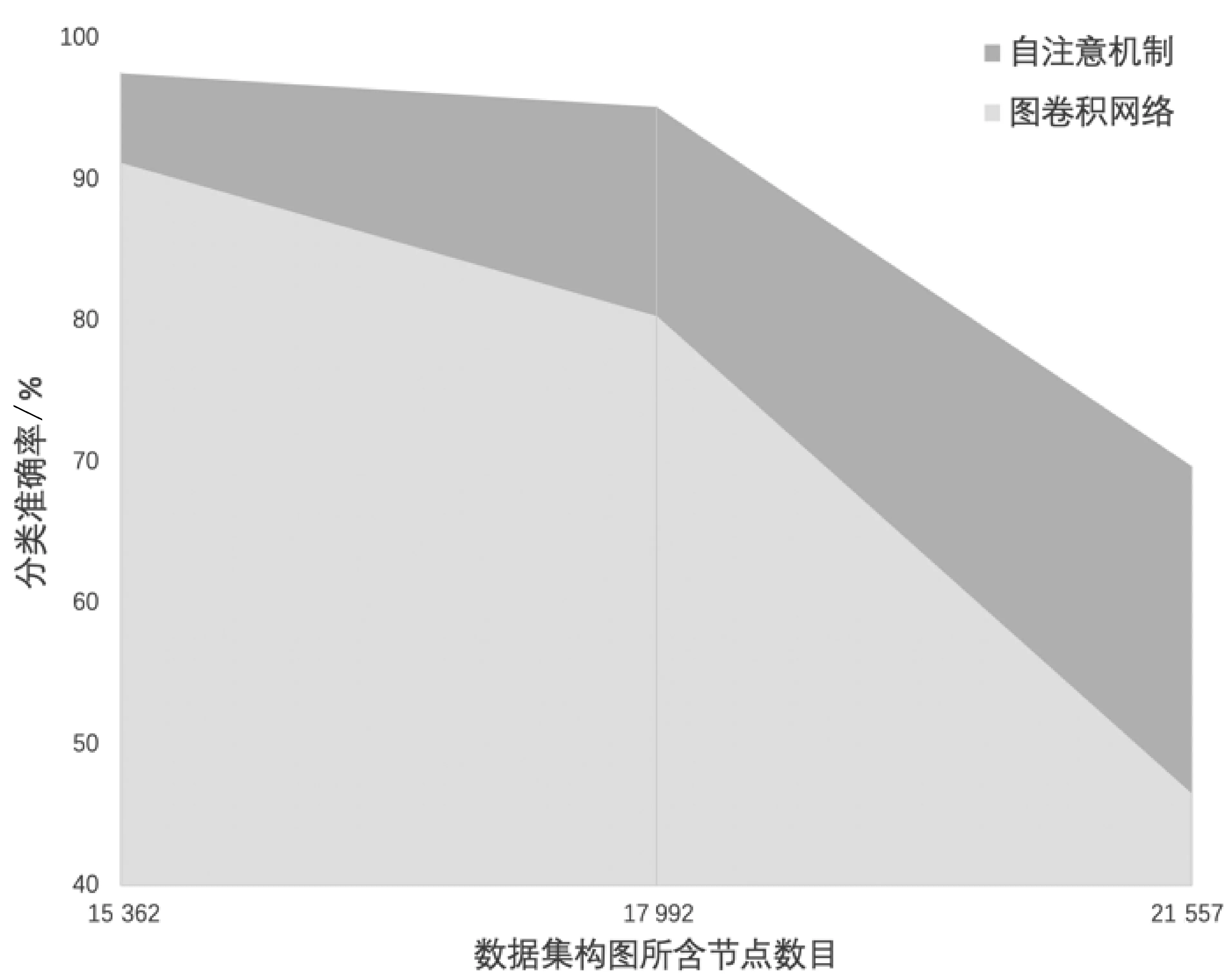
图2 分类准确率差距与数据集规模的关系
我们还发现,使用自注意机制的SA模型在三个文本分类数据集上的分类准确率也都显著优于目前使用图卷积网络最先进的文本分类模型Text-GCN(使用T检验进行显著性检验,满足p<0.05的条件,说明该差异是显著的)。在R52和Ohsumed两个数据集上更是超过了Conv-GCN,达到了目前最先进的文本分类水平。两者在R8数据集上的表现也相当,可归因为参数优化上的随机性。
综合之前的分析结果,这些证据表明,在文本分类任务中自注意机制更具表达能力,或可替代图卷积网络,带来潜在的性能提升。
4 结语
本文对深度学习的两项前沿技术即图卷积网络和自注意机制进行了比较研究,从原理上分析发现,自注意机制可视为图卷积网络的一种泛化形式,具有较图卷积网络更强的表达能力。自注意机制可认为也以所有输入样本为节点,构建有向全连接图进行卷积。此外,图卷积网络中用于表示节点间关系的邻接矩阵往往是训练之前人为预先给定的,而自注意机制中与之相对应表示节点之间连接关系的矩阵则由可学习的参数根据不同任务特性学习得到,即各节点之间连边的权重甚至图的结构都是由可学习的参数根据不同任务的学习目标自适应地决定的。最后,在多个文本分类数据集上进行了图卷积网络与自注意机制的对比实验。结果显示,使用自注意机制的模型较使用图卷积网络的对照模型分类效果更佳,甚至超过了目前图卷积网络用于文本分类任务的最先进水平。并且随着数据规模的增大,两者性能差距也随之扩大。这些证据表明自注意机制更具表达能力,或可替代图卷积网络带来潜在的性能提升。
需要特别指出的是,本文对图卷积网络和自注意机制的讨论实际上是限制在自然语言处理领域内的。除本文的内容之外,还可以许多角度对两者之间的关系进行探讨,例如,在非欧氏度量空间的数据上两者表现的比较、两者的计算代价等,还可以利用可视化的方法在原理上探索两者表现差异的缘由。未来工作中,可以尝试在其他更多任务上进行图卷积网络与自注意机制的对比研究和实验,例如,机器翻译、文本摘要等,甚至是其他领域的任务。考虑到所采用技术的相似性,也可以进一步对融入了注意力机制的许多图神经网络和自注意机制进行对比研究。
