基于BEAVRS基准题高保真建模的OpenMC程序和NECP-X程序的对比验证
2022-01-20沈芷睿孙启政何东豪潘清泉张滕飞彭良辉杨伟焱
沈芷睿孙启政何东豪潘清泉张滕飞彭良辉杨伟焱
1(上海交通大学核能与核技术工程上海200240)
2(上海核工程研究设计院有限公司上海200233)
在数值反应堆高保真建模模拟中,一般采用两类高保真计算程序,分别为蒙特卡罗程序和确定论程序。蒙特卡罗程序主要以MCNP(Monte Carlo NParticle Transport Code)[1]、JMCT(J Monte Carlo Code)[2]、RMC(Reactor Monte Carlo code)和SuperMC(Super Monte Carlo)[3]等为代表;确定论程序主要以nTRACER[4]、Decart[5]和MPACT[6]等为代表。NECP-X是西安交通大学反应堆物理团队开发的确定论核反应堆物理计算程序[7]。OpenMC是由美国麻省理工学院(Massachusetts Institute of Technology)的计算反应堆物理小组开发的程序[8],该程序可进行临界问题和多种固定源问题的计算,也包含了多群功能,主要应用于反应堆物理分析设计;可产生多群均匀化截面,也可以进行缓发中子的产生计数。
反应堆模拟评价和验证基准题(BEAVRS benchmark)提供了典型的美国商用压水堆堆芯的初始运行周期1和重新装载的运行周期2的实测物理数据。该基准题不仅包含了详细的堆芯参数、燃料组成和其他重要组成的参数,还提供了热态零功率条件下和运行时堆芯的详细结果和参数。
蒙特卡罗程序和MOC(Method of Characteristics)方法是高保真计算的代表,现阶段就提高其效率问题展开了许多研究。例如将CAD(Computer-aided Design)转换为蒙特卡罗几何的转换程序CMGC(The CAD to Monte Carlo geometry converter)可以准确地形成CSG(Constructive Solid Geometry),从而提高MCNP程序计算效率[9],同时在SuperMC程序中采用线程级数据分解方法可满足计算全堆芯高保真输运-燃耗计算的存储,又能保持较高的并行效率[10]。MOC方法常被用于确定论程序中进行输运计算,采用低阶角通量非线性差分方程应用于MOC方法可提高计算速度[11]。提高高保真模拟计算的同时,也要保证高保真计算的精度,为验证确定论一步法和概率论方法在高保真计算方面的精度水平。本研究利用确定论程序NECP-X和蒙特卡罗程序OpenMC,分别基于BEAVRS基准题进行高保真建模,通过对基准题模型的部分物理参数进行计算,初步验证了两个程序对复杂堆芯精细建模计算的可行性和准确性。同时,本研究还将比较两个程序对同一模型的相同物理参数的计算结果,分析偏差来源以及两个程序的计算效率,为程序以后的应用及完善提供参考。
1 程序介绍
1.1 NECP-X程序
NECP-X能够对三维全堆芯问题直接进行共振和输运计算。该程序的数据库被分为两部分:多群数据库NECL-MG和连续能量数据库NECL-CE。共振计算中使用了伪共振核素方法,通过共振自屏蔽计算得到有效的自屏蔽截面。伪共振核素是每个燃料棒中所有共振核素的混合物,利用伪共振核素和中间共振近似得到子群概率,并使用丹可夫因子考虑空间自屏效应得到每个燃料棒的等效一维圆柱形问题,将全堆芯问题分解成一组一维问题[12]。NECP-X的全堆芯非均匀输运计算采用了二维/一维耦合输运计算方法,计算二维问题时采用二维特征线法,计算一维问题采用SN方法。同时,还采用了多级并行策略,包括空间区域分解、角度区域分解和特征线并行提高计算效率。NECP-X还采用了MOC方法中常用的粗网有限差分法以加速输运方程中外迭代的收敛速度[13]。
1.2 OpenMC程序
OpenMC是一款三维的连续能量蒙特卡罗反应堆物理开源程序[14]。该程序能够在利用立体几何构造或由CAD构造的三维模型中进行固定源、k-本征值问题等不同的类型的中子输运计算,同时兼具燃耗计算的功能。
OpenMC内置了基于构造性实体几何表示(Constructive Solid Geometry representation)的模型构造方法,利用不同的曲面构造出封闭的空间,即栅元(cell),能够对绝大部分几何体进行准确地构建,避免了由于空间网格离散引入的误差。OpenMC还采用了fission bank算法,减少了不必要的并行通信,能够进行更高性能的并行计算[15-16]。
2 基准题描述
BEAVRS基准题来源于美国西屋公司的一个真实压水堆,该基准题详细描述了堆芯的几何结构以及堆芯的运行参数。
本文对基准题中描述的模型进行了适当地简化。反应堆全高为435.444 cm,包括堆芯网格组件、堆芯围板以及反射层等。每个组件均匀分成17×17个栅元,燃料棒根据235U富集度的不同分为1.6%、2.4%和3.1%三种类型。根据组件在堆芯中的具体位置,每个组件的可燃毒物的排列方式以及个数不同,根据数量可燃毒物可分为12个和16个两种。控制棒材料为Ag-In-Cd[17]。
本文主要对两种堆芯模型进行了高保真建模,模型1为5×5全堆芯模型,其中共含有21个燃料组件,在模型1建模时考虑了轴向支撑格架、定位格架和可燃毒物;模型2为15×15全堆芯模型,其中共含有193个燃料组件,在模型2建模时省略了轴向支撑格架、定位格架和可燃毒物。
利用较为简单的模型1,先验证NECP-X和OpenMC两个程序的建模以及两个程序计算设置的正确性,同时也验证BEAVRS基准题模型进行简化的可行性。此后,利用更接近于真实堆芯情况的模型2,验证两个程序对真实的复杂堆芯精细建模计算的可行性和准确性。
3 计算程序建模
3.1 NECP-X程序建模
在模拟计算中,采用1/4堆芯对称模型以降低计算量。三维算例计算模型:对于UO2非均匀栅格,对燃料区域径向划分5圈,幅角方向划分8区;对于慢化剂区域径向划分3圈,幅角方向划分8区。轴向采用SN求解器,径向采用MOC求解器,MOC特征线线宽为0.025 cm,求积数组采用Chebyshev_Yamamoto求积组,每个卦限内的幅角数与极角数分别为8和3。特征值与注量率的收敛准则分别为1.0×10-5和1.0×10-4。输 运 修 正 采 用inflow方 法,利 用global_local共振计算方法进行共振自屏计算,共振干涉因子方法为pmm,采用能群SPH(Smoother Particle Hydrodynamics)修 正[18]。一 步 法 程 序NECP-X采用64能群结构,轴向采用2个区并行运算,径向采用257个区并行运算,程序在浪潮机架服务器NF5280M5运行,服务器共用39个运算节点,每个节点有40个CPU。以模型2为例,计算不同控制棒组插入情况下的模型2所需时间约为0.72 h。模型1的堆芯组件布置如图1所示,模型2的堆芯组件布置如图2所示。

图1 模型1的堆芯布置(1/4对称)(a)堆芯燃料装载方式,(b)毒药装载方式Fig.1 Core assembly layout of model 1(quarter symmetry)(a)Core fuel loading pattern,(b)Poison loading pattern

图2 模型2的堆芯布置(1/4对称)(a)堆芯燃料装载方式,(b)堆芯控制棒布局Fig.2 Core assembly layout of model 2(quarter symmetry)(a)Core fuel loading pattern,(b)Layout of core control rod
3.2 蒙特卡罗程序
在计算模型中,设置每一代中子数目为2×107个,总中子代数为800代,跳过非活跃代数为100代,同时测量统计每个组件的总裂变能沉积能量。OpenMC程序的计算采用64核并行,在上海交通大学JCLOUD(Jiaotong Cloud)云平台上开展。以模型2为例,计算不同控制棒组插入情况下的模型2所需时间约为21.1 h。模型1的堆芯组件布置如图3所示,模型2的堆芯组件布置如图4所示。
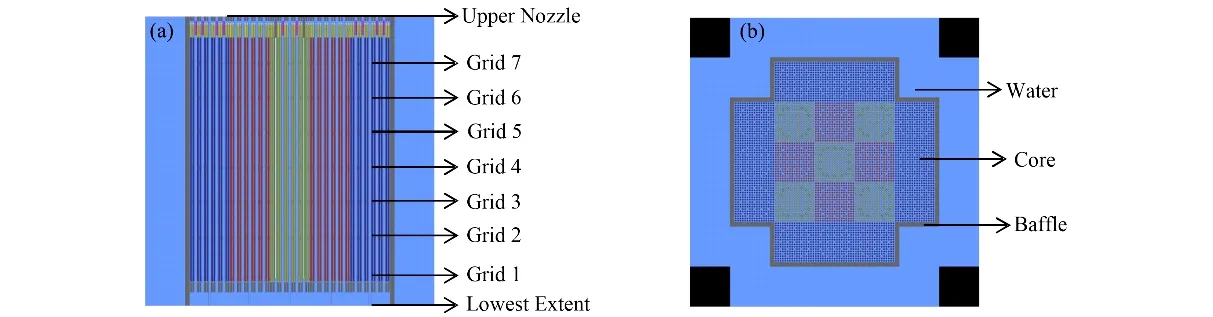
图3 模型1的堆芯布置(a)轴向几何,(b)径向几何Fig.3 Core assembly layout of model 1(a)Axial geometry,(b)Radial geometry

图4 模型2的堆芯布置(a)轴向几何,(b)径向几何Fig.4 Core assembly layout of model 2(a)Axial geometry,(b)Radial geometry
4 模拟结果分析
4.1 模型1
利用确定论高保真程序NECP-X和蒙特卡罗程序OpenMC在相同模型条件下对模型1进行了建模计算,计算了热态零功率(Hot Zero Power,HZP)状态下的有效增殖因子keff。在HZP状态下,反应堆正常运行时没有控制棒插入堆芯,硼浓度为9.75×10-4。两程序截面数据库均采用ENDF/B-VII库。有效增殖因子keff计算结果如表1所示,NECP-X与OpenMC计算结果符合较好,相差为1.37×10-3。

表1 热态零功率下NECP-X与OpenMC有效增殖因子keff结果对比Table 1 Comparison of keff calculated by NECP-X and OpenMC in HZP condition
同时,NECP-X和OpenMC分别计算了HZP状态下的模型1的组件功率分布,HZP状态下的硼浓度相同,均为9.75×10-4。OpenMC预估中子通量的碰撞来计算用户自定义的空间和能量的总反应率,通过总裂变率乘以每次裂变释放的能量得到能量沉积。NECP-X根据不同材料进行分区,计算得到不同材料区的每次裂变生成的能量,最后乘以通量与裂变截面得到功率密度。选取模型1中燃料富集度为1.6%的有17×17个栅元的组件,对1/4组件模型的棒相对功率进行了计算,1/4组件模型的棒相对功率分布如图5所示,相对功率为零的地方插入的是导向管。

图5 1/4组件棒相对功率分布Fig.5 Relative power distribution of rod(1/4 assembly)
两个程序的组件功率计算值进行了相同的归一化处理,两个程序计算所得的组件功率分布趋势相同,均呈现出内部组件功率较高外部组件功率较低的趋势。同时,还以NECP-X程序计算值为参考,计算并统计了两个程序的组件功率计算值的相对偏差和平均绝对偏差。组件功率的相对偏差分布情况如图6所示,相对偏差的最正偏差为0.79%,最负偏差为-0.80%,平均绝对偏差为0.55%。NECP-X与OpenMC的组件功率计算结果符合较好,组件功率相对偏差较大的组件多为堆芯的外围组件,其功率水平较低。在模型1中,两个程序关于HZP状态下的有效增殖因子keff和组件功率的计算结果符合较好,误差在可接受范围内,验证了模型和两个程序的计算参数设置的正确性。

图6 组件功率的相对偏差分布Fig.6 Relative deviation distribution of assembly power
4.2 模型2
模型1的验证结果,为模型2建立模型和设置计算参数奠定了基础。由于模型2更为复杂,因此适当增加了每代粒子数目以及总代数。
利用确定论程序NECP-X和蒙特卡罗程序OpenMC在相同模型条件下对模型2进行了建模计算,计算了HZP状态下的有效增殖因子keff。在HZP状态下,反应堆正常运行时仅有控制棒组件D在213步,硼浓度为9.75×10-4。两程序截面数据库均采用ENDF/B-VII库。有效增殖因子keff计算结果如表2所示,NECP-X与OpenMC的keff计算结果符合较好,相差为4.5×10-4。

表2 热态零功率下NECP-X与OpenMC有效增殖因子keff结果对比Table 2 Comparison of keff calculated by NECP-X and OpenMC in HZP condition
NECP-X和OpenMC还计算了7组控制棒组在分别完全插入状态下的有效增殖因子keff,结果如表3所示。

表3 插入不同控制棒组件NECP-X和OpenMC keff计算结果Table 3 Results of control rod bank worths
硼浓度与HZP状态下的硼浓度相同,均为9.75×10-4,唯一变量为不同控制棒组插入[19]。有效增殖因子keff随控制棒组插入而减小,反应性也随之降低。不同控制棒插入时keff减小程度不同,不同的控制棒组对反应堆反应性影响的大小不同。对两个程序的keff计算结果进行比较,NECP-X的计算结果相对于OpenMC的计算结果均偏小,其中计算结果最大偏差为5.9×10-4和6.0×10-4,说明两个程序的keff计算结果符合较好。表4给出了对应的7组控制棒价值的计算结果,对反应堆反应性影响最大的控制棒组均为控制棒组D,比较两个程序的控制棒价值计算结果,OpenMC对于控制棒组C的棒价值计算结果相对于NECP-X的计算结果较大,且该计算结果的偏差远远大于其他几组控制棒组棒价值的偏差。两个程序的计算结果中控制棒价值最大偏差为4.9×10-4,不超过5.0×10-4。NECP-X与OpenMC的控制棒价值计算结果符合较好。
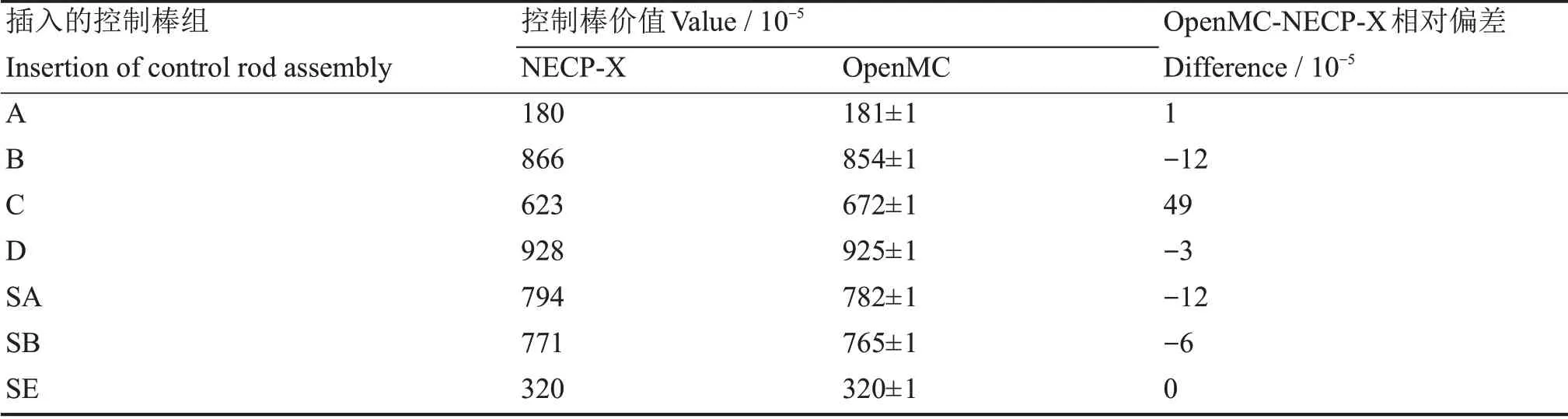
表4 控制棒价值结果Table 4 Results of control rod bank worths
同时,NECP-X和OpenMC还计算了该7组控制棒组分别在完全插入下的组件功率分布。对两个程序的功率计算值进行了相同的归一化处理。本文以NECP-X计算值为参考,计算统计了两个程序的组件功率的相对偏差和平均绝对偏差。图7列出了7组控制棒插入情况下两个程序组件功率计算值的相对偏差的分布。
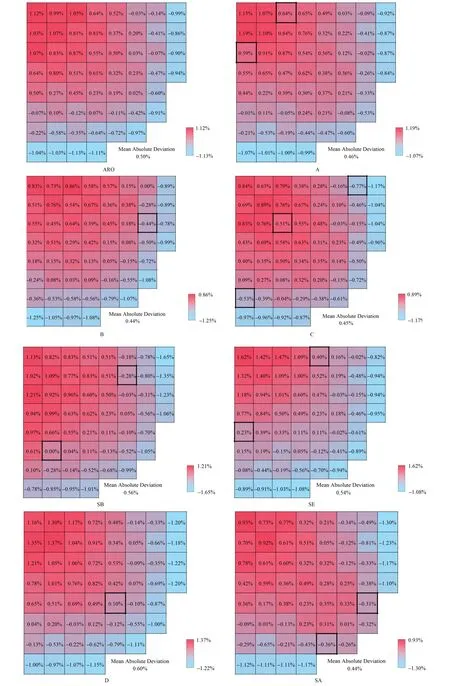
图7 组件功率的相对偏差分布Fig.7 Relative deviation distribution of fuel assembly power
在控制棒全提工况下,两组程序计算得到的组件功率分布均呈现内部和外部组件功率较低,与BEAVRS基准题所给出的组件功率分布趋势符合较好。与控制棒全提工况下的组件功率分布相比,插入控制棒组的组件相对功率明显减少且为最低,同时其周围组件的相对功率也明显减少,而其他组件的相对功率显著增加。NECP-X程序计算得到的组件功率分布严格对称,而OpenMC程序由于计算结果本身存在标准差,组件功率分布不完全对称。
不同控制棒组插入工况下的组件功率相对偏差分布中,相对偏差最大为1.62%,出现在控制棒组SE组全插入的工况下;相对偏差最小为-1.65%,出现在控制棒组SB组全插入的工况下。
组件功率分布相对偏差并不严格对称,OpenMC计算得到的组件功率结果存在标准差,自身的计算过程中会引入一定的偏差。同时,蒙特卡罗计算过程中所设置的每代粒子数和总代数也会影响计算结果,增加每代粒子数和总代数可减少计算结果的标准差但同时也会增加计算所需要的时间。同时,当堆芯功率很低时也会发生功率倾斜现象。
除此现象之外,组件功率相对偏差较大的组件多为堆芯的外围组件,即富集度为3.1%的燃料组件,这与模型1中组件功率相对偏差的分布情况相似。外围组件靠近反射层,NECP-X模拟计算时,靠近反射层部分的组件相对于内部的组件计算和模拟更为复杂,但因为外围组件的绝对组件功率值较低,所以对keff的影响较小。
为了更好地分析组件功率分布相对偏差分布现象的原因,本研究同时对组件功率相对偏差的最正偏差、最负偏差以及平均绝对偏差进行计算统计,结果如表5所示。

表5 组件相对功率计算值偏差(%)Table 5 Results of full assembly power distribution deviation(%)
组件功率平均绝对偏差在0.60%以内,插入控制棒组D组时平均偏差最大为0.60%,插入控制棒组B组和SA组时平均绝对偏差最小为0.44%。虽然部分工况下部分组件的相对功率偏差超过1%,但各个工况下的组件相对功率平均绝对偏差均小于0.60%,说明NECP-X与OpenMC的组件功率计算结果符合较好。
5 结语
本文使用了NECP-X和OpenMC程序对大型压水堆基准题BEAVRS进行了高保真建模模拟计算。建模对象包括HZP状态下的有效增殖因子、7组控制棒的控制棒价值以及不同控制棒组件分别插入情况下的组件功率分布。计算结果表明:两个程序的计算结果偏差在可接受范围内,有效增值因子最大偏差为1.37×10-3,控制棒价值最大偏差为4.9×10-4,组件功率评价偏差在0.60%以内。通过对BEAVRS基准题的建模计算,初步验证了NECP-X和OpenMC在高保真建模、临界计算、功率分布预测等方面的准确性与可靠性,同时也为两个高保真程序的计算效率和实际反应堆堆芯模拟方面提供了借鉴和参考。后续将对BEAVRS基准题的多循环算例进行高保真模拟计算和对比验证。
作者贡献声明沈芷睿直接参与论文研究,实施研究,采集、分析并解释计算数据,并负责撰写论文;孙启政协助使用程序;何东豪指导程序的使用以及数据的采集,对论文的知识性内容做审阅;潘清泉负责论文的修改;张滕飞负责论文的修改,对论文的知识性内容做审阅;彭良辉提供技术支持;杨伟焱提供技术支持。
