电信号在离散系统中的时域与z域分析

林 琳

（湖南城市学院 信息与电子工程学院，湖南 益阳 413000）

0 引 言

在信号与系统的分析中，离散系统的分析方法可分为时域解法和变换域解法。对于连续系统可以采用s域分析法进行分析，而对于线性离散系统可以采用z域变换法进行分析。z变换对于描述系统的差分方程转变为代数方程起到关键性作用，且代数方程中包括了系统的初始状态，进而可以求得系统的零输入响应、零状态响应以及全响应[1]。

1 离散系统的时域分析

线性时不变（Linear Time Invariant，LTI）离散时间系统用常系数线性差分方程进行描述，即：

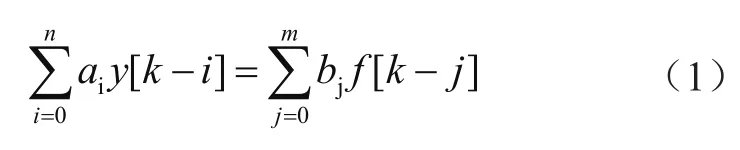
式中，f[k]和y[k]分别表示系统的输入和输出。

在已知差分方程的初始状态以及输入的条件下，可以通过编程迭代算出系统输出的公式为：

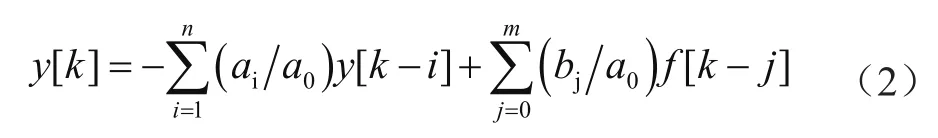
系统的零状态响应就是在系统初始状态为零条件下求微分方程的解。在零初始状态下，MATLAB控制系统工具箱提供了一个Filter函数，可以计算差分方程描述系统的响应[2]。

离散系统的冲激响应、阶跃响应分别是输入信号为δ(k)和u(k)所对应的零状态响应。MATLAB控制系统工具箱专门提供了两个函数求解离散系统的冲激响应和阶跃响应。

卷积是信号与系统中一个最基本也是最重要的概念之一。在时域中，对于LTI连续时间系统，其零状态响应等于输入信号与系统冲激响应的卷积。而利用卷积定理，这种关系又对应频域中的乘积。MATLAB信号处理工具箱提供了一个计算两个离散序列卷积和的函数conv。

2 离散系统的z变换

如有序列f[(k](k=0,±1,±2,…)，z为复变量，其双边z变换为：

如果式（3）的求和只在k的非负值域进行，则称为序列的单边z变换[3]。

线性时不变离散系统可用其z域的系统函数H(z)表示，通常具有的有理分式的形式为：

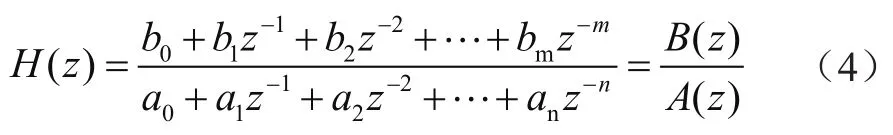
为了能从系统的z域表示方便地得到其时域表示式，可将H(z)展开为部分分式和的形式，再对其求逆z变换[4]。MATLAB的信号处理工具箱提供了对H(z)进行部分分式展开的函数residuez，其调用形式为：

式中，B和A分别为H(z)的分子多项式和分母多项式的系数向量，r为部分分式的系数向量，p为极点向量，k为多项式的系数向量。

由此借助于residuez函数将上述有理函数H(z)分解为：

进一步通过上面介绍的求逆z变换的方法求出系统的单位序列响应。通过系统函数的表达式，可以方便地求出系统函数的零点和极点。系统函数零点和极点的位置对于系统的时域特性和频域特性有重要影响。位于z平面的单位圆上和单位圆外的极点将使得系统不稳定。系统函数的零点将使得系统的幅频响应在该频率点附近出现极小值，而其对应的极点将使得系统的幅频响应在该频率点附近出现极大值[5-7]。

在系统函数的零极点分布问题上，可以借助函数TF2ZP来直接得到系统函数的零点和极点的值，并通过函数zplane来显示其零点和极点的分布[8]。利用MATLAB中的impz函数和freqz函数可以求得系统的单位序列响应和频率响应。假定系统函数H(z)的有理分式形式为：

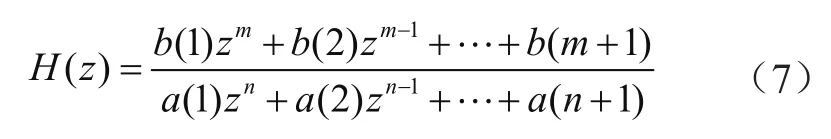
TF2ZP函数的调用形式为：

式中，b和a分别表示H(z)中的分子多项式和分母多项式的系数向量，z为求出的零点，p为求出的极点，k为增益。

该函数的作用是将H(z)转换为用零点、极点以及增益常数组成的表示式，即：

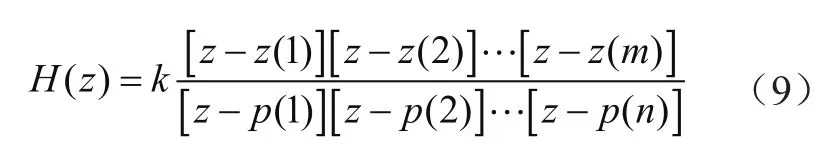
zplane函数的调用形式为zplane(b,a)，该函数的作用是在z平面画出单位圆以及系统的零点和极点[9]。

3 在离散系统时域分析中对信号进行滑动平均滤波

滑动平均滤波法又称递推平均滤波法，对于离散系统而言，其实现方法为连续取N个采样值看成一个循环队列，队列的长度固定为N，每次采样到一个新数据放入队尾，并扔掉原来队首的一个数据，即遵循先进先出的原则。滤波器每次输出的数据总是当前队列中的N个数据的算术平均值。其优点在于对周期性干扰有良好的抑制作用，平滑度高，适用于高频振荡的系统。而缺点就是灵敏度低，对偶然出现的脉冲性干扰的抑制作用较差，不易消除由于脉冲干扰引起的采样值偏差，不适用于脉冲干扰比较严重的场合，比较占用RAM资源。

滑动平均滤波算法的基本思想是设定一个宽度固定的滑动窗口，该窗口沿着时间序列滑动，同时取窗内数据的算术平均值作为输出值。而由输出值组成另一个数字序列，也就是滤波后的序列。设2k+1为滑动窗口的宽度，输入输出分别为x(n)和y(n)，则：

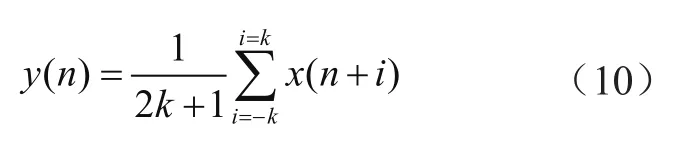
在MATLAB中可以采用filter函数实现滑动平均滤波，设原始数据为x，平均窗口设为a（a为正整数），那么无权重滑动平均后的数据y为：

设一个离散系统其输入信号为f[k]=s[k]+d[k]，其中s[k]=(2k)×0.9k是有用信号，d[k]是噪声信号。利用MATLAB分别绘制出受干扰信号f(k)（有用信号和噪声信号的叠加信号），有用信号s[k]和噪声信号d[k]，如图1中所示为滤波前的3个信号。利用MATLAB中的filter函数对受干扰信号f(k)进行滑动平均滤波，图2中y[k]为经过滤波以后的去噪信号，s[k]为原始的有用信号。对比图2中s[k]和y[k]可以发现在离散系统时域分析中引入滑动平均滤波可以有效抑制噪声，基本还原了原始有用信号，实现了去噪处理。

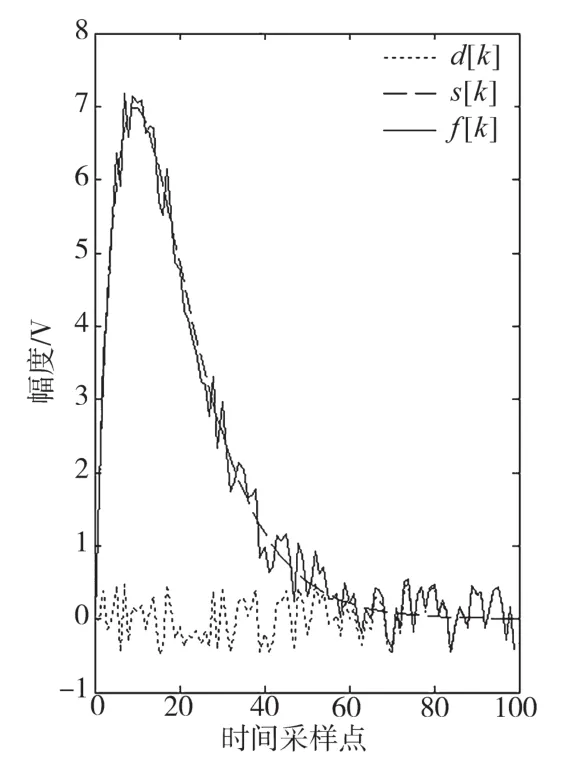
图1 有噪声信号

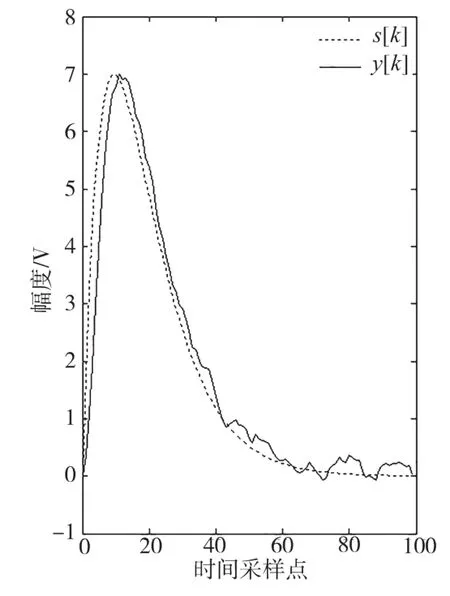
图2 去噪后信号

4 离散系统中利用z域分析确定零极点

z变换可将离散时间序列变换为在复频域的表达式。离散时间信号的z变换是分析线性时不变离散时间系统问题的重要工具，在数字信号处理和计算机控制系统等领域有着广泛应用。

z变换域没有物理意义，只是一种数学手段，之所以在离散系统分析中引入z变换的概念就是为了简化分析方法和过程，为系统分析研究提供一条新的路径。这种方法的数学描述为z变换及其逆z变换，被称为离散系统的z域分析法[10]。

在z域下，系统函数H(z)的零极点分布完全决定了系统的特性，若系统函数的零极点已知，则系统函数便可确定下来。系统函数的零极点分布对离散系统特性的分析具有非常重要的意义。

零极点在z平面上的分布如图3所示，该系统的所有极点位于z平面单位圆内，故系统为稳定系统。

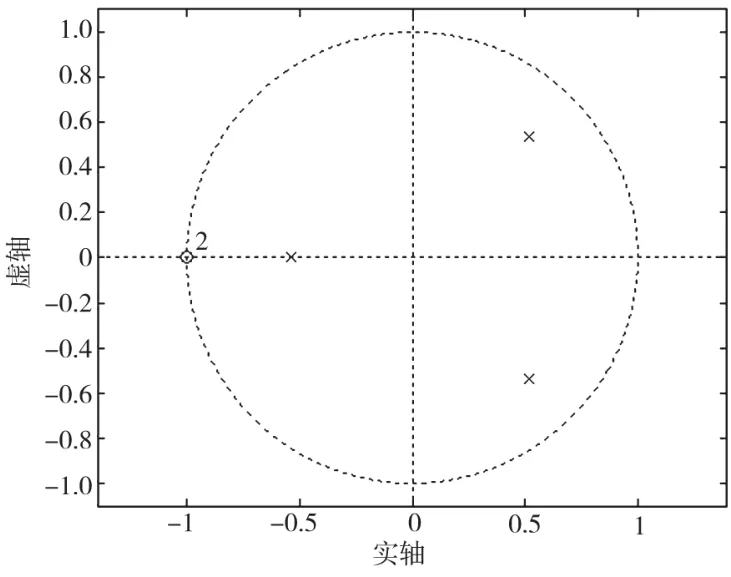
图3 零极点在z平面上的分布

5 结 论

离散系统的时域分析和z域分析对离散信号的分析具有非常重要的意义，是对离散信号进行分析的重要数学工具。其中z域分析可以简化分析过程，为离散系统的分析提供另一条路径，在数字信号处理和计算机控制系统等领域得到广泛应用。