LWE问题的分析策略及格基约减算法综述
2022-01-20王镭璋张帅领王保仓
王镭璋, 张帅领, 王保仓
(1.西安电子科技大学 综合业务网理论及关键技术国家重点实验室, 陕西 西安 710071; 2.中国电子科技集团公司 第三十研究所, 四川 成都 610041)
由于格密码具有抗量子、高效率、最坏情况/平均情况等价性和丰富的密码功能等特点引起了学术界的广泛关注。第一个基于格的加密方案是由Ajtai等[1]提出的。后来Regev[2]对该方案进行了简化和改进。Regev工作的主要成果之一就是引入了带错误学习问题(Learning With Errors, LWE),该问题在密码构造中使用相对简单,并且至少同最坏情况下SVP的变体问题一样难[2]。目前,LWE问题已被证明是加密应用程序的通用构建模块([Regev05][2]、[GPV08][3]、[BV11][4]和[ABB10][5])。因此,对LWE问题求解算法的深入分析对深刻理解格密码安全性非常重要[6]。
对LWE问题的一个标准求解做法就是用Kannan嵌入[7]将其归约到某个格上的唯一最短向量问题(unique Shortest Vector Problem,u-SVP)。而求解格上最短向量问题的主流做法是采用格基约减算法进行求解。格基约减算法作为格密码分析研究的核心内容,其中对格基约减算法的预测和优化仍是目前一个活跃的研究领域[8]。虽然已有的研究在理论上确实给出了格基约减算法在最坏情况下性能的边界定理[9-18],但这些边界是渐近的,在应用于实际甚至密码实例时不一定严格[11,14,19]。对这些算法行为的预测依赖于启发式和近似,其中一些预测已知在某些特定的范围内会失效[11,20]。随着格基约减算法的标准化,对其性能的精确估计也就成为一个关键的问题。
1 预备知识
定义1 格:已知m中的n个线性无关的列向量组B={b1,…,bn}(m≥n),这组向量的所有整系数线性组合的集合称为格L,记为
其中,线性无关的向量组B称为格L的一组基。n为格的秩,m为格的维数。
定义2 最短向量问题(SVP):给定m中秩为n的格L的一组基B,寻找一个非零向量u∈L(B),使得u是L(B)是非零最短向量,即u满足λ1(L)。
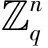
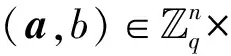
2 LWE问题的分析策略以及非基于格的求解算法
2.1 LWE问题的分析策略
目前,对于不同类型LWE问题的分析方法主要分为4种策略: SIS 策略、BDD 策略、ISIS策略和直接求解(Direct)策略,见图1。
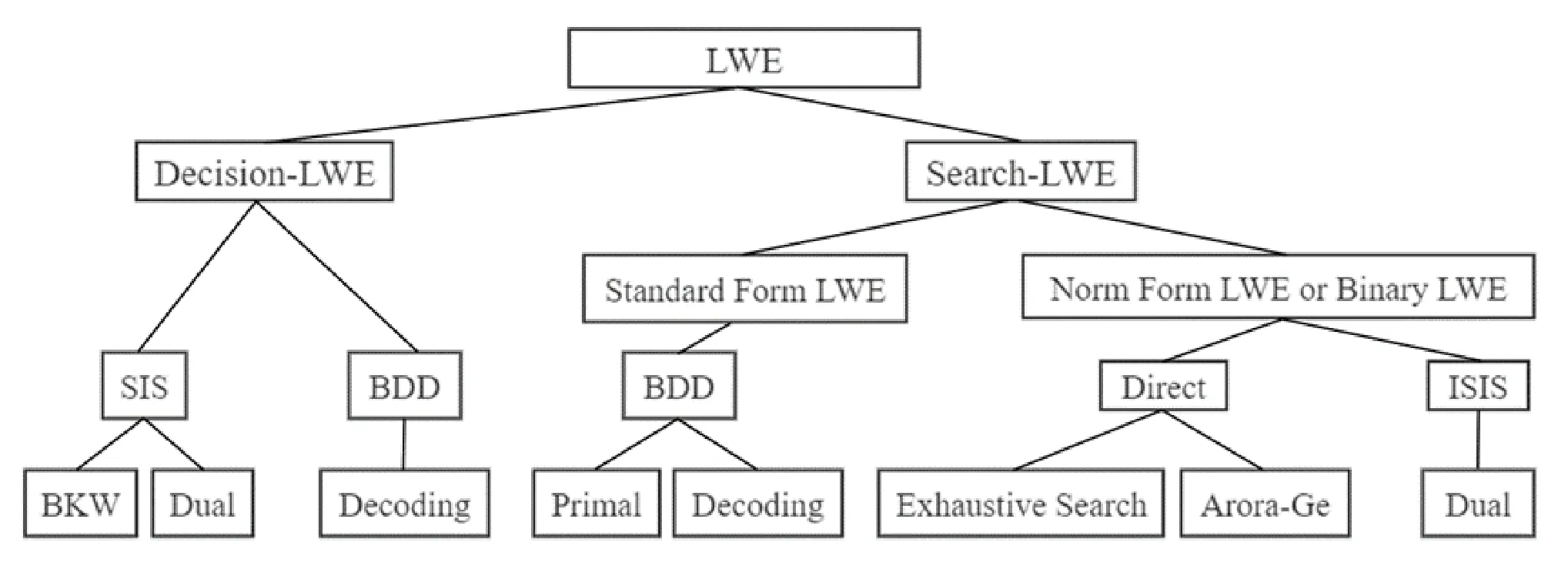
图1 LWE分析策略及方法Fig.1 LWE analysis strategies and methods
对于不同策略下的求解算法主要有4种:组合算法、代数算法、基于格的原始攻击和基于格的对偶攻击。非基于格的求解算法就是组合算法和代数算法2种。组合方法一般指BKW算法[21],该算法可看作一种扩展的高斯消元法,一次处理多个元素,这种算法最大的问题是需要指数多的样本。 代数方法是Arora-Ge算法[22],该方法是一种非线性化方法,同样需要指数多的样本。思想就是将LWE实例分成单项式相乘的形式,从而通过求解单项式的根将秘密向量s各个分量恢复出来。算法关于维数是指数的,对于错误向量较小的情况可以降到亚指数级别。下面对组合方法和代数方法分别进行详细描述。
2.2 非基于格的求解算法
2.2.1 组合算法
组合算法的代表算法是BKW算法,这是一种特殊的对偶攻击方法,最早由Avrim Blum,Adam Kalai和Hal Wasserman提出用来求解LPN问题,该算法能够以亚指数的时间复杂度2O(n/logn)求解LPN问题。由于LWE问题可看做LPN问题从2到q上的扩展,因此,扩展版本的BKW算法适用于分析不限制样本量的LWE类问题,基本思路是通过分块碰撞的思想,借助广义生日攻击的方法在指数多的样本中挑选出部分样本使其加和为0,此时零向量关于样本的系数向量即为对偶格中的短向量,由本节中介绍的对偶攻击可知,这些对偶格中的短向量可以用作LWE实例的区分器。
具体来说, BKW构造短向量vi的方法如下:给定一组样本2,BKW分解行向量的n个分量为a个块,每个块的宽度为b=n/a。算法共分成a个阶段,第i个阶段通过充分多的上一级样本碰撞(加法运算)获得第i块元素全零的样本。假设初始样本数量为2aqb,在最优的情况下,算法结束时可获得qb个长度为的短向量,使用这些短向量做区分攻击的方法与对偶攻击中的区分方法类似,即每个短向量的区分优势为ε=exp[-2π22a(σ/q)2],大约需要1/ε2个短向量来获得不可忽略的区分成功率,因此,BKW需要通过调整分块方式来平衡区分优势与样本数量以获得最优的算法复杂度。
BKW算法的主要改进技术包括:Albrecht等[23]在PKC 2014上提出的Coded-BKW算法中求解小密钥版本的LWE问题所采用的Lazy Modulus Switching技术;2015年,文献[24-25]分别独立提出的通过使用不同大小的分块平衡BKW算法复杂度的技术;2017年,Guo等[26]提出的在BKW算法中结合筛法的改进技术,该算法是当前具有最优时间复杂度的BKW类算法。
2.2.2 代数攻击——Arora-Ge算法
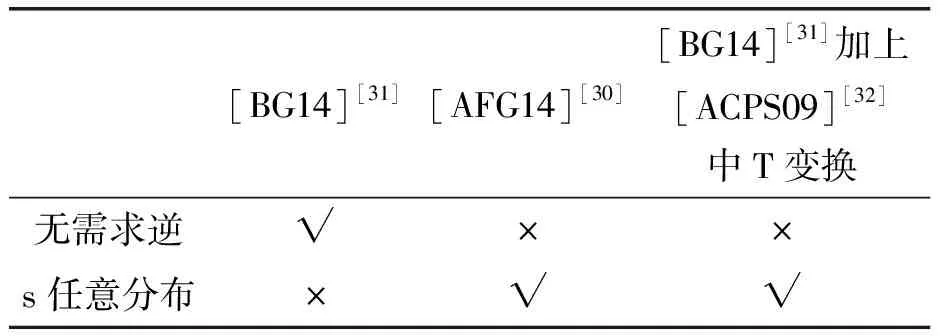
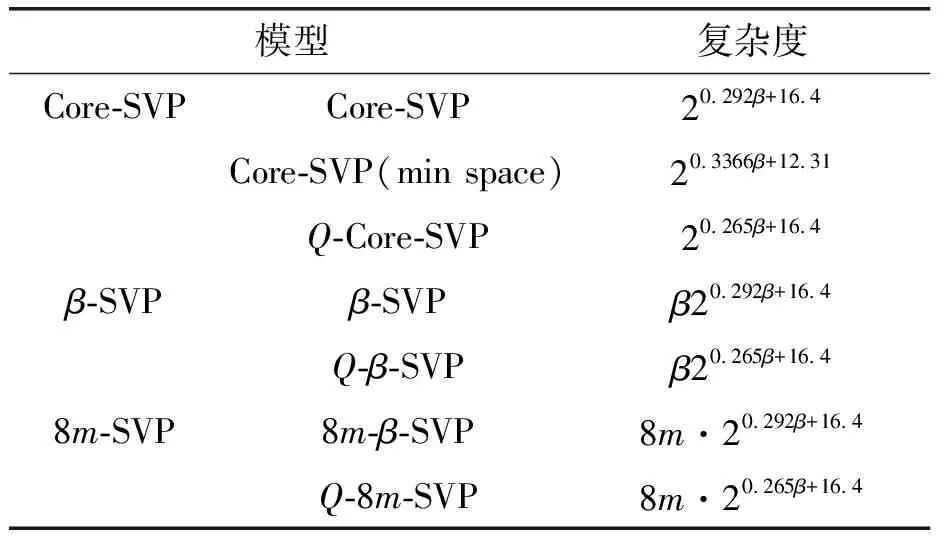
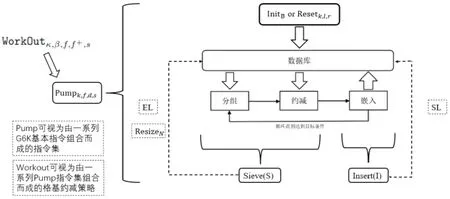
代数攻击最早由Arora等[22]提出,适用于不限制样本量的LWE类问题,它的基本思路是:构建以错误e为根的无噪音非线性多项式方程组,通过代换所有单项式构成线性方程组并求解。具体来说,给定LWE实例矩阵(A,b=As+e),根据错误分布(高斯分布和小均匀分布等)的性质可知错误分布e在有界区间[-t,t]中(t∈,d=2t+1 由于BKW算法和Arora-Ge算法需要指数级别的实例数,而现实中的格基加密方案至多泄露关于LWE实例维数n的多项式多个实例([Regev05]型加密方案至多泄露nlogq个实例,[LP11]型加密方案[28]至多泄露2n个实例)。因此,针对实际方案的攻击,以上2种求解算法均无法实施。针对实际方案的攻击一般使用的是基于格的攻击方法。 针对判定性LWE问题采用SIS策略,归约到求正交格上短向量。针对搜索型LWE问题,根据其秘密向量s的模长大小采用不同的策略。如果是标准型(Standard form)LWE问题则采用使用BDD策略的原始攻击或是Decoding方法;如果是Normal Form LWE或是Binary LWE应当充分利用秘密向量s的模长很短这一信息,从而应该使用ISIS策略的对偶攻击。 3.1.1 SIS策略 3.1.2 BDD策略 [LP11][28]中的Decoding策略强于区分攻击,因为Decoding策略直接将噪声向量e恢复出来,实际也可以视为是求解Search-LWE问题的一种方法。但该策略在使用比区分攻击质量更差的格基时仍有着一样甚至更好的优势。其基本思想是将LWE实例中将b视作Λq(A)格上BDD问题的目标向量,然后直接利用最近平面算法找到距离b最近的格点As。该策略成功当且仅当错误向量e落到P1/2(B*)内下面给出直接使用Babai算法[29]找到格点As的概率估计: LP最近平面算法,[LP11][28]中的优化最近平面算法在每一次执行寻找当前距离目标向量最近的超平面操作时,从原先的只选距离目标向量最近的超平面改成:选择di个超平面(i∈+),如此将P1/2(B*)往每个方向上扩大为原来的di倍,使得e落入P1/2(B*)的概率增大。同时,新算法要记录下全部个候选值,并分别计算它们到目标向量b的距离,取其中距离最小的作为其优化最近平面算法输出结果。如此在付出次对(B,b)的Babai算法的计算开销下,算法的成功率增大为 3.2.1 BDD策略-原始攻击 针对搜索型LWE问题,BDD策略先是将搜索型LWE问题归约到某个q-ary格上的BDD问题,再利用Kannan嵌入[7]将q-ary格上的BDD问题归约到最终构造格上的uSVP进行求解。根据LWE问题中s的分布不同,最终构造的格基的形式有所不同。 最早提出该策略的是文献[28],特别地,给定分布Ls,通过采样获得实例满足: 其中,A2是由均匀采样获得,e来源于错误分布, 另外阶模q下可逆方阵。在文献[28]中通过不断地从分布Ls,中抽取生成新的实例直到这些实例形成可逆方阵A1,并直接丢掉其余实例。易知: 其格基矩阵M为 以上提到2种格攻击一般称为原始攻击,其成功条件(08估计[10]见3.2.3节) 是相同的,即2种格基在求解标准型LWE 问题本质上没有区别。 3.2.2 ISIS策略-对偶攻击 针对秘密向量s很短的正规型LWE问题,以及二进制型LWE问题,除了使用BDD策略的原始攻击,[BG14][31]提出了一种更高效的求解策略:将Normal Form(Binary)型LWE问题视为ISIS问题进行求解,充分利用了s也很短这一信息。一般将使用ISIS策略的[BG14]型攻击称为对偶攻击[31]。归约的思路可以概况如下: Normal Form(Binary) LWE≤ISIS≤BDD≤u-SVP, 其中,第三个不等号处使用了Kannan嵌入。更详细的过程如下: 给定服从分布Ls,选取的m个LWE实例考虑ISIS实例: 存在整系数线性组合u=(s|*|1),使得uM=(s|e|1)是Λ(M)上短向量。 3.2.3 2种攻击方式的比较 上述2种不同攻击策略的区别在于:Bai等[31]的格基更有效地利用了s与e同分布时,s也是很短的这一信息,相较于原始攻击中的格基[30],文献[31]有更弱的攻击成功条件。下面先给出求解u-SVP的理论条件再对2种攻击进行更详细的比较。 原始攻击的格基的gap为 而对偶攻击的格基的gap为 此外,Bai等[31]的格基无需实例组成的n阶方阵要在模q下求逆,因此对实例的数量没有严格的要求。但原始攻击中的格基因为需要实例组成的n阶方阵要在模q下可逆,因而只能用于求解实例个数m大于n的情况。 值得注意的是Bai等的格基也只能用于求解Normal Form LWE(s与e同分布)问题,对s取自均匀分布的Standard LWE问题无法直接使用。而原始攻击的格基就不存在这个问题,它们的格基对s取任意分布的LWE问题都是适用的。值得注意的是,对于Standard LWE问题,可以使用T变换[28],在花费不超过O(n2)的实例下,将其转化为Normal Form LWE问题。从而使用Bai等的格基去更高效地求解。2种不同的格基优劣势见表1。 表1 Primal攻击中2种不同格基的优劣势 文献[30]中有结论:对于普通形式的LWE(除Normal Form LWE以外),Kannan嵌入和Dual嵌入的效果基本无差别。 该估计与BKZ类算法的实际实验结果更为贴切。目前,NIST第三轮中基于LWE困难假设方案的比特安全强度均采用这种由文献[33]中提出的保守估计(采用最为保守Core-SVP模型,详情见表2)[34-35]。该估计通过选择试遍实例数m的可取值(对标准型LWE来说m∈(0,nlogq),对Normal Form和Binary 型LWE来说m∈(0,2n)),求出当前m下使得上述不等式成立的最小β值的方法,找到使得攻击开销最小的(m,β)对,最后用Core-SVP模型估计出求解方案的安全参数设置下LWE问题的计算开销作为方案的比特安全强度。 表2 SVP求解器复杂度估计模型 使用文献[33]中的估计对上述2种攻击策略与使用08估计[10]得到的结论一致。 3.2.4 对Binary型LWE问题攻击的加速技术 另外,针对Binary LWE问题,其秘密向量s的每个分量都取自{0,1}或{-1,0,1},使用全同态加密中的模转换技术和文献[31]中的Rescale技术,可以让最终构造格基的gap增大,降低攻击算法的复杂度。此外,利用组合攻击也可以一定程度上降低求解秘密向量分布稀疏的LWE问题复杂度[36-38]。 (1)模转换技术 模转换是全同态加密中为加速模乘运算速度提出的技术。因为固定其他参数、缩小模数,将使得计算效率提升。但注意到模转换技术虽然减少了模数,但也将引入一部分额外的噪声。对于求解LWE问题来说,噪声的增大会导致LWE问题的求解越发困难。因此将大模数q换成小模数p的模转换操作需要合适地取p的值。 其中,u∈,e′∈[-0.5,0.5],x,yp表示在模p的意义下对向量x和y求内积。 如上文所述,当模数p减小时,算法的时间复杂度会降低;但是当p取得过小时,又会造成噪音规模的增加,导致解决这个实例的困难度增加,因此,p的取值需要平衡这两者之间的矛盾。最优的p值的选择可以使得(p/q)·a-「(p/q)·a⎤,s≈|(p/q)·e|,即在模转换后的错误规模大致放缩为原来的p/q,据此,可以计算出p的最优取值约等于 模转换技术可用于原始攻击和对偶攻击中。 (2)Rescale技术 Rescale技术由Bai等[31]在2014年提出,这种技术可以被应用在Dual嵌入中,并将其称为BG嵌入。在BG嵌入中,嵌入格被修改为L(M)={x∈νn×m+1|x·(A|Im|-b)T=0modq}形式,基且有(s|*|1)·M=(vs|e|1)。在普通的Dual嵌入情况下时, 当v=1,由于s每个分量很小或很稀疏时,向量(s|e|1)的各个部分的模长是不一样长的。要使才能将目标向量的各个部分变成均衡的,即需要选择合适的v值使得可以使得调整后的向量 (‖vs|e|1‖)就是L(M)中的一个最短向量,且利用格基约化算法找到它变得更加高效[31]。因为实际实验表明格基约减算法更加倾向于输出每个分量值都比较均衡的短向量[34]。以为例,有因此,令可以算出那么有 (3)组合攻击 在秘密向量s取值稀疏的情况下, 如{0,1}或{-1,0,1}采用组合攻击[36-39],即给一个秘密s最多w 经过上述分析可知,无论是求解判定性LWE问题还是求解搜索型LWE问题,都是通过构造某个格基将LWE问题转化为构造格上的u-SVP问题进行求解,或是对构造格的格基进行约减得到质量足够“好”的格基,从而能够成功解码出目标向量。所以高效的格基约减算法是求解LWE问题的主要方法。作为求解近似SVP和近似CVP的近似算法,目前主要的格基约减算法有LLL、基于枚举的BKZ类以及基于筛法的General Sieve Kernel(G6K),其中,基于近些年筛法发展最新结果的G6K是当前最快的格基约减算法。在简单地回顾经典的LLL和BKZ类之后,将着重介绍G6K算法。介绍格基约减算法之前,首先将BKZ类以及G6K算法所基于的SVP求解算法做一下梳理。 4.1.1 枚举法 枚举算法的优势是算法开始后是确定性的,且只使用多项式大小的空间。其缺点就是时间复杂度是超指数的O(2nlog(n))。此外,多年来已经开发了一些优化和启发式方法,使得枚举目前在实践中对于较小的维度最具吸引力。枚举是一种通过系统地枚举空间中某个给定半径的超球(通常是n维平行六面体或椭球体)内所有格点来解决任意格上最短向量问题(SVP)和最近向量问题(CVP)的标准技术。人们对格枚举技术的兴趣主要是由于它们的低内存需求(关于格的维数n是线性的),以及在中等低维数上优异的实际性能。枚举算法的运行时间在很大程度上取决于输入格基的质量。因此,使用格基约减算法对输入格进行适当的预处理是枚举法的重要组成部分。最早考虑执行预处理后再做枚举的是文献[40-41],其中,文献[40]使用的是LLL算法作为预处理,经过LLL算法处理后,再执行枚举求解出最短向量的开销是2O(n2)。而Kannan[41]提出了一种更加复杂的预处理方法,对枚举算法进行低维递归调用,将(总)渐近运行时间减少到nO(n)。文献[42]则给出了Kannan算法在最好情况下时间复杂度的最优分析。文献[42]表明Kannan算法求解SVP的时间为nO(n/(2e))。然而,由于其指数时间的预处理开销,对实际可以执行枚举算法的维数n来说,Kannan算法并不比渐近复杂度更劣势的方法(如文献[40]基于多项式时间格基约减算法的变体)快。2015年,Micciancio等[43]引入了 Kannan算法的变体,该算法的渐进时间是同Kannan算法一样的nO(n),但文献[43]所需预处理开销更少,使得该算法在中低维的枚举方法中有着很强的竞争力。在实际使用时,枚举算法的有效实现需要大量使用浮点运算,但由于舍入误差和精度问题,浮点运算可能相当棘手。有关使用浮点运算的SVP枚举的详细分析,请参阅文献[44]。 2021年,文献[45-48]将近几年枚举的新技术,如文献[45-47]中放松裁剪枚举算法条件的技术,以及文献[48]中扩展预处理技术相结合,提出了渐进复杂度更低的枚举算法,其渐进复杂度为nO(n/(8))。此外,他们将这个新的枚举算法应用到BKZ(2.0)算法中,减少了基于筛法实现的BKZ算法[13]与基于枚举实现的BKZ算法之间实际性能的差距[49]。 4.1.2 筛法 筛法是通过在固定半径的球壳上堆积格点来求解最短向量问题。2001年,Ajtai等[50]提出的随机筛法被认为是最早且最著名的指数空间复杂度算法之一,它的时间复杂度和空间复杂度均为2O(n)。其后,Regev[51]、Nguyen等[52]、Micciancio等[53],先后给出了AKS筛法更准确的时间和空间复杂度估计,分别为23.4n+o(n)和21.97n+o(n)。Micciancio等[53]提出了一种确定性的算法,ListSieve该算法将时间和空间复杂度分别改进到了23.199n+o(n)和21.325n+o(n),该方法结合生日攻击可以在22.465n+o(n)的时间内找到最短向量。2015年,Aggarwal等[54]基于离散高斯采样提出了新的随机算法,将时间复杂度进一步改进到了2n+o(n),此外,在启发式假设下,筛法的复杂度上界可以进一步降低。2008年,Nguyer等[52]基于AKS筛法提出了第一个随机启发式筛法,分别达到了20.415n+o(n)和20.207 5n+o(n)的时间和空间复杂度,其他启发式筛法的改进工作还包括二重筛法和三重筛法[55-58]等,当前已知最高效的经典计算机模型下的筛法是由Anja等[59]提出的,该算法实现了时间和空间复杂度的平衡,2者均见文献[59-60]。在量子计算模型下,Larhoven等[60]通过Grover算法将上述筛法的时间复杂度进一步改进为20.265n+o(n)[60]。Voroni细胞算法是由Daniele等[61]于2010年提出的一种新型确定性算法,该算法利用格点的Voronoi细胞结构,将求解相关向量问题的方法用于求解最近向量问题的预处理,其时间和空间复杂度约为22n+o(n)和2n+o(n)。 4.2.1 LLL算法 LLL算法是一个多项式时间算法[62], 可视为是在二维拉格朗日/高斯算法在高维空间上的扩展。理论上,LLL算法的Hermite因子根可以达到δ0=(4/3)(n-1)/4n≈1.075,而实际运行LLL算法的输出结果要好过其理论结果,LLL算法的Hermite因子根实际可达1.021 9[10]。在小维数格上,LLL算法甚至能求出最短向量。 LLL算法的细节描述: 定义5 (LLL约减基) 一组基B={b1,b2,…,bn}∈n称为L(B)的δ-LLL既约基,如果以下条件成立: 1.∀1≤i≤n,j 下面的定理说明了,这样的基是存在的并且能够在多项式时间内找到。 定理1任给格基B={b1,b2,…,bn}∈n,任意1/4 LLL算法的实现细节: 输入:格基b1,b2,…,bn∈n及参数y; 输出:L(B)的y-LLL约减基. 2. 循环for(i=2,2≤i≤n,i++) 3. 循环for(j=i-1,1≤j≤i-1,j--) 5.endfor 6.endfor 8.bi↔bi+1 9. goto 1 10.endif 11. 输出b1,b2,…,bn 接下来,给出y-LLL约减基的一些性质,为了表述简单,令y=3/4,对于其他的1/4 性质:令b1,b2,…,bn为格L∈n的一组LLL既约基,为其相应的Gram-Schmidt正交化,则 3. 对任意t≤n个线性无关向量x1,x2,…,xn∈L,则对1≤j≤t,有 4.2.2 BKZ类算法 (1)BKZ算法 BKZ算法是由Schnorr等[9]应用分块约减的思想改进LLL算法而提出的。衡量BKZ算法的关键参数是分块大小的β,β越大,BKZ输出约减基的质量越好,输出的最短向量也越短,但同时算法运行时间也越长。 BKZ算法的每一轮会依次在L[i:i+β]上运行枚举算法(其中,i∈{1,2,…,n-β},当i∈{n-β+1,…,n}时,则在L[i:n]上运行枚举算法),并将枚举出的最短向量嵌入格基B,然后用LLL算法去除线性相关性,从而逐渐提高格基质量。当某一轮运行结束后,最短向量模长与上一轮输出的结果相比没有改变,则BKZ算法终止,并输出当前的最短向量。下面给出BKZ算法输出基的质量和算法运行时间的估计。 1)质量估计 2)时间估计 (2)BKZ2.0算法 2011年,Chen等[14]对BKZ算法进行了4点改进,得到BKZ2.0算法[65]: 1)提前终止算法:原始BKZ算法的运行终止条件是执行完本轮约减得到的格基较之上一轮约减得到的格基没有任何变化,则终止BKZ算法。但文献[11]等实验表明,BKZ算法执行一定的轮数后,继续执行BKZ算法对格基质量的改善作用越来越少。但要达到格基不能作进一步改善的条件,仍需执行很多轮BKZ。因此,BKZ2.0将算法的终止条件改成格基的质量无明显改善时终止。 2)极度裁剪:如4.1.1小节中所描述那样,枚举通过搜索固定某个半径内的n维平行六面体或椭球体内所有的格点来解决任意点阵上最短向量问题。Gama等[68]通过重复多次:随机地裁剪掉搜索空间中绝大部分格点,只枚举剩下的少量格点的极度裁剪枚举,获得了总时间开销更少的枚举算法。 3)强预处理:原始的BKZ算法在执行前是使用LLL算法做格基的预处理。BKZ2.0算法采用比输入分块大小更小的BKZ算法做BKZ2.0算法执行前的预处理。这样虽然使得预处理的开销比原来大,但能获得比LLL算法输出基质量更高的预处理结果,如此可有效降低调用枚举算法的计算开销[37]。 4)优化枚举算法的搜索半径:原始BKZ算法调用枚举算法求解投影子格上的最短向量时枚举空间的搜索半径都是固定的。但实际上随着枚举的层数逐渐增加,目标向量下一个坐标的可能取值范围是逐渐减少的。BKZ2.0对枚举每一层的搜索半径进行了估计,并用优化的估计半径代替了原先固定的大半径,减少了枚举算法的计算开销[14]。 其中,2)~4)有3个改进的目的都是减少BKZ在调用枚举算法时的计算开销。 此外,基于BKZ2.0算法,2021年,Albrecht等将放松裁剪条件[45-47]以及扩展预处理等技术[48]相结合提出了新的BKZ算法,减少了基于筛法实现的BKZ算法[13]与基于枚举实现的BKZ算法之间实际性能的差距[49]。 (3)Progressive-BKZ算法 2016年,Aono等[45]对BKZ算法中分块长度β的取值方式进行了更细致的分析,提出了渐近型BKZ(Progressive-BKZ,P-BKZ)算法。P-BKZ算法与BKZ,BKZ2.0最大的不同就是其分块的大小不是固定的,而是随着P-BKZ算法的执行由一个小的初值逐渐增大。P-BKZ算法通过合适选取的分块大小初值和递增值,使得算法整体的时间复杂度最优。与BKZ2.0相比,P-BKZ算法在解决最高160维的SVP挑战(SVP challenge)[15]时比BKZ2.0最多可以快约50倍[45]。 (4)BKZ算法模拟器 最早的BKZ模拟器由Chen等[14]提出。此后Aono等观察到BKZ约化基Gram-Schmidt范数曲线相对于GSA 曲线的“头部凹陷”现象并提出了分析和利用它提升BKZ效率的方法,并作出一个新的模拟程序。2017年,Yu等[69]进行了大量实验对BKZ的实际行为进行了评估,对于BKZ约化基Gram-Schmidt正交化后范数的分布进行了更为细致的研究,并且通过观察结果更准确地量化了“头部凹陷”现象。2018年,Bai等[70]通过考虑随机格中短向量的分布又提出了一个更为精确的BKZ模拟程序,很好地模拟并解释了“头部凹陷”现象,并利用该现象构造了Pressed-BKZ算法。同时指出该现象随着分块大小的增大而不再明显,在分块大小约为200时,该现象几乎完全消失。 (5)Slide-BKZ算法 (6)对BKZ类算法计算开销的估计 根据文献[72]中的实验结果,一些研究者将时间成本估计式中的o(β)省略或者替换为常数16.4。另外,文献[72]还对空间和时间综合考虑,在空间复杂度最低的情况下,成本模型中的参数c=0.336 6,o(β)替换为常数12.31。在进行安全性评估时,根据考虑的SVP oracle调用次数,可将其分为3种模型: Core-SVP模型[33]、β-SVP模型[73]和8m-SVP模型[36]。值得注意的是,文献[13]的结论指出8m-SVP模型是一个过高的估计(不再保守),但文献[13]的结论仍未打破Core-SVP模型的下界,因此,使用Core-SVP模型进行估计仍是保守的。 4.3.1 G6K算法的CPU实现 General Sieve Kernel(G6K) 是Albrecht等[13]于2019年提出的一种基于筛法的可以执行各类格基约减策略的抽象状态机。这个抽象的状态机可以通过调整不同的约减策略去执行目前已有的各种格基约减算法,如经典的BKZ算法。但值得注意的是,经典BKZ算法是基于枚举算法作为其在约减过程中求投影子格上最短向量时的Oracle调用,而G6K是基于筛法执行其格基约减策略的。同时,使用筛法的G6K不仅仅像经典BKZ类那样将枚举算法作为一个黑盒调用,只输出一个短向量,而是构造了一个筛法的数据库,存储着筛法筛出的大量相当短的向量。 G6K结合并扩展了近年来筛法的最新优化改进成果,其中主要代表是Ducas[19]在2018年欧密上对子筛法的研究。提出对于求解n维格上SVP,对这个n维格的n—d维投影子格做筛法,而不是对n维完整格做筛法,并利用最近平面算法从投影子格筛出的候选短向量中提升出n维完整格上最短向量的策略。将求解n维格上SVP降低至求解n—d维投影子格上SVP,理论上d=O(n/logn)时,Ducas证明子筛法均可成功[19]。实际上自由维数d的取值可能比理论估计更大,需要根据实例具体实验才能准确得到。此外,G6k中还利用的一项技术是Laarhoven等[74]在2018年PQC 上提出的渐进筛。其主要思想与Progressive BKZ的想法类似,从小的投影子格开始做筛法,然后逐渐增大所筛子格维数,利用投影子格上已筛出的短向量组成的数据库加速加入新格基向量后做筛法的速度。下面给出这2个技术的详细描述。 (1)Dimension for free[19] Ducas 提出的Dimension for free(Dimforfree)技术。Dimforfree技术的主要思想是:对于要求解的n维格上最短向量问题并不是像之前一样对整个n维格直接进行筛法求解,而是只需几次调用在n—d维原格投影子格上的筛法,以及利用低维格上的最近平面算法,将投影子格上求解出的短向量提升到n维完整格上的最短向量的组合算法。如此,就将最耗时的筛法所筛格的维数从n维降至n—d维。其中,d=n/logn时,Ducas[19]证明该子筛法仍能够成功,尽管Ducas这个改进的提升只是亚指数的2n/logn,但在实际实验中有显著的提升效果。需要指出的是,具体实现时,Ducas同样没有找到一个很好的对d的准确估计,只能通过实际测试的方法从大的d值逐渐减少,直到d减少到能求出原问题的解。 Ducas的具体做法是:d先选一个很大的值,如n/4,然后d每次减少1,直到子筛法最终找到最短向量(d减小到n/logn时,就达到理论上子筛法成功条件了),取更大的d纯粹为了更快求解。 对n维格的n—d维投影子格Ld做筛法: Ducas利用Dimforfree技术构造了一个能求出近似HKZ 约减基的子筛法+算法,最后,再用输出的近似HKZ 约减基V代替当前格L的格基向量,作为新的输出格基B。具体做法就是利用LLL 算法对[V|B]进行约减,并去除其中线性相关的部分。 (2)[LM18] 渐近筛法[74] [LM18] 渐近筛法的基本思想是首先对输入格基做格基约减的预处理。其次从某个维数小于完整格的维数子格开始做筛法,筛出的结果中实际上已经包含了很多短的格向量,通过这些信息,可以更快地找到完整格上近似最短向量。一个更清晰地解释渐进筛比经典筛法更快的理由是:当筛法输入的格基约减程度越高(格基质量越好),那么在较低维数的子格中,筛法会找到更短的格向量并将其添加到列表L中,而列表中有更短的向量,意味着:扩大子格维数后,重新抽样得到的新的格向量可以更容易更快地被已经在列表中的短向量所约减。由于在经典的筛法(直接在高维格上执行筛法)中需要花费更长的时间先找到(近似)较短的格向量。同时经典的筛法不能像渐进筛一样,在这种加速约减中获益(在每一个低维子格中筛出的更短向量都将有助于列表中向量的质量,让下一次抽样出的新向量被更短的向量所约减)。[LM18][74]相信在很大程度上解释了当使用约减程度更高的格基作为渐近筛的输入时,所带来的计算效率上的有效提升。 渐进筛相较于经典筛法的优势在于:更少的迭代次数就能求出SVP的解,更少的内存开销,预处理对其求出速度影响更为明显,更容易预测筛法的行为。 介绍完G6K 算法中使用的主要改进筛法的技术后,再对G6K 算法本身进行描述。 (3)G6K 算法内部状态、指令和约减策略[13] 所有被G6K所考虑的向量都在投影子格L[l:r]中。更准确地说,w=B[l:r]·v∈d,其中,v∈n。用格点w在投影格基B[l:r]下的坐标向量v来表示格点。这种表示转换的开销为O(n2)。接下来定义3种对向量分量的扩展或是缩减操作: 1)G6K内部状态表示 -格基B∈d×d在每次使用最近平面算法做提升操作有新的格向量嵌入时需要更新,同时,B的Gram-Schmidt正交基B°也要随着更新。 -位置参数0≤k≤l≤r≤d。[l:r]表示筛法所筛投影子格所在格基的下标范围,[k:r]表示提升嵌入格向量时,嵌入格向量可嵌入的格基下标范围。定义n=r—l为所筛子格维数。 -用db表示对投影子格L[l:r]做筛法筛出的N个格向量组成的数据库。 -候选嵌入向量ck,…,cl, 其中,ci∈L[i:r]或ci=⊥。 2)G6K基本指令 -InitB:初始化格基。对G6K状态机进行初始化,初始格基设置为B∈d×d。 -Resetk,l,r:重置格向量数据库db。将格向量数据库设置为空集,并设置参数(k,l,r) -Sieve(S):对选中投影子格做筛法,并将筛出的短向量通过最近平面算法嵌入到合适位置。在执行对L[l:r]的筛法过程中,将筛出的短向量嵌入到L[k:r]上的合适位置。如果嵌入能改善格基的质量,则称on-the-fly lifting。 -(ER,SL,EL):右扩展,左缩减,左扩展。向右或向左增加或减少数据库中每一个向量的分量。 -Insert(I):根据评分函数选择最优的嵌入位置ci,其中,k≤i≤l。同时,每次嵌入需要更新格基。如果没有合适的嵌入位置,则继续运行SL以确保所筛法能正常终止。 -ResizeN:将数据库大小调整至N。当需要缩减数据库大小时,将数据库中最长的向量移除;当增大数据库大小时,则抽样新的格向量加入到数据库中。 3)G6K约减策略表示 作为可以执行不同格基约减策略的抽象状态机。首先将G6K的基本指令按要执行约减的策略组合成称为Pump的指令集合: 其中,0≤k≤k+β≤d,0≤f≤β,s∈{0,1}控制在Pump-down阶段是否执行筛法。Resetk,k+β,k+β表示对数据库的重置,其中,k确定此次Pump中数据库格向量可嵌入位置的下标下界。Pump-up阶段利用子筛法和渐进筛的思想,每次迭代对数据库中全体格向量执行一次左扩展(EL)操作:将数据库中全体格向量利用Babai算法从L[i:r]提升到L[i—1:r]后(其中,i∈[l+1,r]),都要对整个数据库执行一次筛法(Sieve(S)操作)。经过β-f次迭代以后,获得存有大量短的格向量数据库db,随后进入Pump-down阶段。Pump-down阶段中据评分函数[31,75]将L[l:r]格中筛出的短的格向量提升嵌入到L[k:r]中评分最高的位置,得到新格基。嵌入操作利用Dimforfree技术和嵌入评分函数,实现了对格基的质量提升。 最后,G6K利用一系列Pump指令集合的组合,刻画不同的格基约减策略: WorkOutk,β,f,f+,s:Pumpk,β-f+,β,s,Pumpk,β-2f+,β,s,Pumpk,β-3f+,β,s,…,Pumpk,f,β,s, 其中,f+表示每次迭代Pump时,所筛投影子格维数的递增量。整个G6K算法实现的整体框架可以用图2表示。 图2 G6K算法整体框架图Fig.2 Overal frame diagram of G6K algorithm 图2中的分组步骤是G6K所基于的启发式筛法在执行格向量约减前的一个分组操作。不同启发式筛法的最主要区别就在于它们对向量的不同分组方法,从而导致它们的时间复杂度和找到相对接近向量对的性能不同。以经典的BGJ筛法为例介绍分组过程:利用NNS技术[75],首先将数据库中众多格向量用一个个超锥体分成多个不同的组,其中同一个组中的格向量与指示超锥体方向的中心向量夹角小于某个预设值。分组后考虑同一组中格向量对之间是否存在约减,而不是考虑整个数据库中全部可能的向量对组合是否存在约减。如此可有效减少筛法的计算复杂度。详情见BGJ筛[75]以及BDGL筛[59]。 G6K算法默认执行的格基约减策略是:首先将r设置为d(d是输入格基的维数),l设置为d—n0,其中,n0表示首次Pump的投影子格维数上界(默认取值是40)。Pump-up阶段中每次Pump的初始子格维数为30,经过Pump-up完成对L[l:r]投影子格的渐进筛。随后进入Pump-down阶段,根据评分函数将L[l:r]格中筛出的短向量嵌入到L[k:r]中的合适位置并更新格基。下一次Pump时,采用子筛法的思想,使用Lift先将整个数据库中格向量提升到L[l-f+:r]中,即令l=l-f+,将下一次Pump所筛投影子格维数上界增大f+(f+默认值是3),再次迭代。直到某次Pump时,嵌入的格向量模长小于预设的目标向量模长,就终止程序并返回最短格向量,或是当前Pump的子格维数达到β-f也终止算法。 因此,通过调整k,β,f,f+,s可以构造各种约减策略不同的格基约减算法。例如,经典的BKZ算法的约减策略可以写成: NaiveTourβ:WorkOut0,β,WorkOut1,β+1,…WorkOutd-β,d,…,WorkOutd-1,d [LM18][74]中滑动窗口(Sliding-window)策略可以表示成: SlidingWindowTourβ: Reset0,0,0,(ER,S)β,(Il,S,ER,S)d-β,(Il,S)β. 此外,G6K在Pump的初始阶段默认采用Gauss筛法以确保初始时不遗漏太多格向量。随着Pump的进行,对维数大于40的投影子格,G6K默认使用hk3筛法。随着筛法技术的进步,可以将更快或是空间复杂度更小的筛法替换掉G6K当前所使用的筛法。 4.3.2 G6K的GPU实现 2021年,Ducas等[76]利用NVIDIA GPU Tensor核心的高效矩阵计算能力极大加速了G6K算法执行筛法时对向量分组和向量约减的效率。同时,所引入的Dual-hash技术在G6K算法执行EL操作时过滤掉了很多并不值得提升的向量,有效减少了提升操作的开销。 提升了此前只使用CPU实现的G6K算法的计算效率,同时极大地降低了能耗(对180维随机格上SVP挑战,GPU实现的能耗不到CPU实现能耗的4%)。他们在Darmstadt的SVP挑战中创下了求解180维随机格上求最短向量的纪录,此前最好的纪录由CPU实现的G6K算法创下,只能求到155维。 本文整理并比较了目前求解LWE问题的分析策略,并对目前主要的格基约减算法的思想和所使用的技术进行了梳理。对于不同类型的LWE 问题, 虽然分析策略有所不同,但大都可以用格基约减算法完成求解。对于现有的格基约减算法,仍有很多改进的地方,例如,如何通过优化底层筛法去降低G6K算法的GPU实现所需的内存开销,利用G6K所定义的抽象状态机找到约减效果更好的格基约减策略,等等。此外,如何更准确地预测格基约减算法输出基的质量,从而能够对基于LWE问题的困难性构造密码方案的安全性更准确地估计也是笔者下一步工作的重点。尤其是对诸如G6K等新的格基约减算法输出基质量的预测,目前尚无很好的估计,笔者将在未来对这一问题做进一步的研究。3 基于格的求解方法
3.1 判定性LWE问题
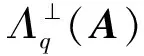
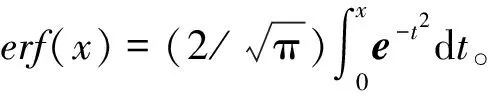
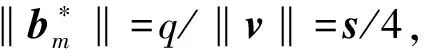
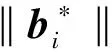
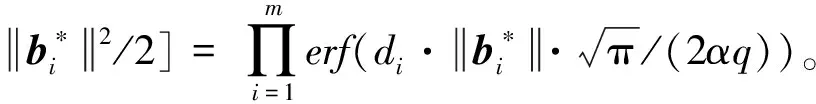
3.2 搜索型LWE问题
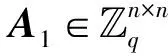
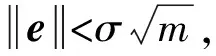
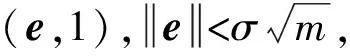
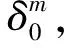

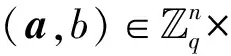
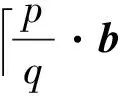
4 格基约减算法
4.1 SVP求解算法
4.2 对经典格基约减算法的梳理
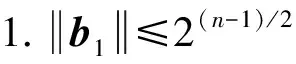
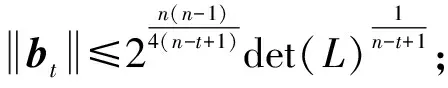
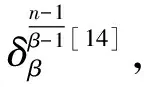
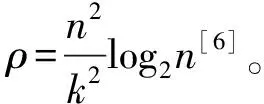
4.3 G6K算法
5 总 结
