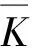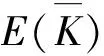离散对数求解算法
2022-01-20庄金成朱玉清
庄金成, 朱玉清
(1. 山东大学 网络空间安全学院/密码技术与信息安全教育部重点实验室, 山东 青岛 266237; 2. 北京交通大学 智能交通数据安全与隐私保护技术北京市重点实验室/计算机与信息技术学院, 北京 100044)
1 离散对数问题定义和应用
1.1 离散对数问题和应用
一般地,给定一个代数系统G(运算记作乘法),元素g和幂数x,指数运算是计算gx。指数运算的逆运算是对数运算,即给定元素g,h∈G,求x使得gx=h,或者证明这样的x不存在。
特别地,当幂数属于一个离散集合(常用的是整数集合)时,对应的运算称为离散指数运算,对应的逆问题称为离散对数问题。本文主要讨论基于有限群的离散对数问题,基本的情形定义如下:给定一个有限群G,|G|=N以及元素g,h∈G,求解整数0≤x≤N-1使得gx=h,整数x称为h相对于g的离散对数,也记为loggh。
离散对数问题本身是算法数论中的一个重要研究问题。Gauss证明模任意素数p存在原根,对应的指标求解问题就是一类重要的离散对数问题,在求解高次同余方程中有重要应用。和通常的对数一样,通过预先计算的离散对数可以将对应的乘法运算转化为加法运算。在通常离散对数定义变形得到的Zech对数(也称Jacobi对数)也有很多应用[1]。
离散对数问题在密码学中可以应用于线性反馈移位寄存器的生成序列和相关的伪随机数生成器[2]。1976年,Diffie等[3]提出了公钥密码学的概念,设想基于陷门单项函数设计公钥密码体制,并且在Gill的建议下采用模指数运算(其逆函数即为离散对数)为设想的单向陷门函数,在此基础上设计了第一个公钥密码系统,即Diffie-Hellman密钥交换体制。1978年,Rivest等[4]基于整数分解问题设计了第一个公钥加密和数字签名体制。离散对数和整数分解问题是经典的公钥密码体制中使用最广的2类困难问题,并且2者的求解算法有很多相似之处。
Diffie-Hellman密钥交换体制优势之一是提供了前向安全性[5],此后离散对数问题被用来设计功能更丰富的密码体制。例如,ElGamal[6]基于离散对数问题设计了公钥加密方案,Schnorr[7]基于离散对数问题设计了身份认证和签名方案,美国国家技术标准局[8]基于离散对数制定了数字签名标准。此外,Diffie-Hellman体制和ElGamal体制的设计思路还对后量子密码方案的设计有所启发,如基于编码的密码方案[9]、基于格上困难问题的LPR加密方案[10]。
公钥密码学中最早使用的离散对数问题是基于有限域的乘法群,后来扩展到基于其他代数的结构,包括基于椭圆曲线上有理点的加法群、基于超椭圆曲线的Jacobian、基于代数数域的理想类群和基于特定代数整数环等[11]。其中,基于椭圆曲线的离散对数问题应用尤其广泛,具体定义是给定有限域q上的椭圆曲线E和有理点P,Q∈P,求解整数x使得Q=xP。Miller[12]和Koblitz[13]独立地提出基于椭圆曲线离散对数问题的密码学方案设计。椭圆曲线离散对数问题还应用在SM2、SM9和一些基于区块链技术的协议等密码方案中。
1.2 离散对数问题变体
根据不同的应用场景,上述基本的离散对数问题有一些变体。
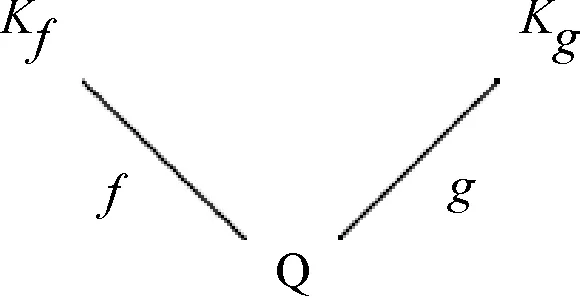
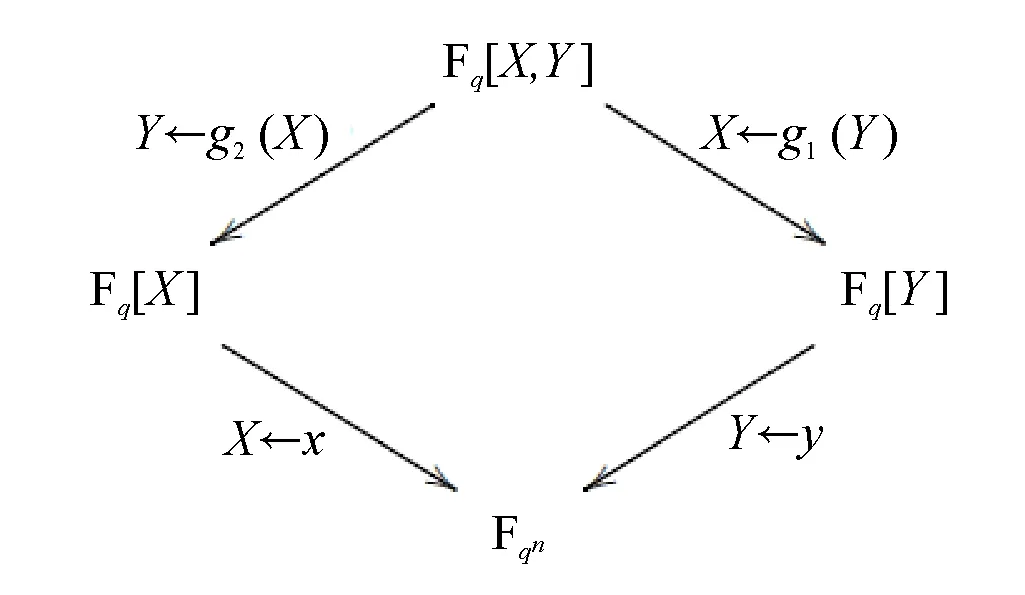
在一些应用中可能限定离散对数的取值范围,或者通过侧信道等技术获得部分信息从而缩小了求解范围。例如,如果已知离散对数0≤x 如果已知离散对数x的二进制中1的个数较少,对应的称为低Hamming重量离散对数问题。 如果给定一个生成元g和多个目标元素h1,h2,…,hn,对应的称为多目标离散对数问题。 如果给定多个生成元素g1,g2,…,gn和一个目标元素h,对应的称为高维离散对数问题,也称为表示问题[14],可以应用于设计电子货币等。 实例压缩问题是指给定m个实例(gx1,gx2,…,gxm),是否可以压缩到n(n 离散对数问题还有一种变体称为带辅助输入的离散对数问题,即在具有辅助输入gx,gx2,…,gxd的情形下加速离散对数x的计算。 Diffie和Hellman设计的两方密钥交换协议基于的更精确的困难问题是Diffie-Hellman问题,随机选择整数a,b,c,计算版本的定义是给定g,ga,gb,计算gab。 判定版本是区分ga,bb,bab与ga,bb,gc。基于Diffie-Hellman问题可以实现密钥交换协议,如基于身份的加密[15]、陷门函数[16]等。 离散对数问题和Diffie-Hellman问题之间是否等价是一个重要的公开问题。 Diffie-Hellman问题的一个重要推广是基于双线性对的双线性Diffie-Hellman问题[17]。给定素数阶循环群G1,G2,G3,密码学中的双线性对是指存在如下映射 e:G1×G2→G3, 满足双线性、非退化和易于计算的性质。密码学中常用的双线性对实例包括有限域椭圆曲线上的Weil对和Tate对。双线性对密码学包含了丰富的密码功能,包括3方的一轮密钥交互[18],基于身份的加密[19]、短签名[20]和群签名[21]等。 Boneh等[22]设想了基于多线性映射可以设计功能更加丰富和强大的密码体制。 在密码学应用中更多是按照一定的分布随机选择平均情况的实例,平均情形的困难性和最坏情形困难性的关系对于密码应用具有重要意义。 离散对数问题通过随机化方法可以建立最坏情况到一般情况的自归约[23]。假定要求的目标元素是h∈G= 一些格上的困难问题也可以建立最坏情况到一般情况的归约,如最小整数解问题(Short Integer Solution,SIS)和容错学习问题(Learning With Errors, LWE)。区别是离散对数是同一个群上的归约,而后者是从任意的格归约到给定的平均情形困难问题。 考虑一般循环群上的离散对数问题,如果G=g上的离散对数是困难的,Hastad等[24]证明对于随机选取的满足|G|=q=p′2k,q的二进制表示为n比特,那么x的k到n-1比特以很高的概率是求解困难的。 整数分解问题和离散对数问题既是公钥密码学应用最广泛的2类困难问题,针对2者的求解算法也有相似之处,包括量子算法和经典算法。Shor[25]设计了量子算法求解整数分解问题和素域上的离散对数问题。 2者都可以看作特殊的隐藏子群问题,例如,基于有限循环群上的离散对数计算等价于求解下面映射的核: φ:2→G, 其中,φ(a,b)=gahb。 更一般地,求解基于交换群的隐藏子群问题有高效的量子算法[26]。 下面讨论经典计算模型(如Turing机)下求解离散对数问题的算法。 Shanks[28]利用时间-空间折中的思想设计了求解离散对数的小步-大步法,该方法是确定性求解算法,而且渐进复杂度优于穷搜法。 x=am+b,0≤a,b 为了求解对应的a,b,注意到有等式(碰撞) gb=hg-am。 可以通过寻找碰撞的方法求解。首先,计算(b,gb),0≤b 为了降低空间复杂度,可以采用伪随机游走等方法设计概率求解算法。 2.5.1 Pollard Rho方法 针对基本的离散对数问题,Pollard[31]基于生日碰撞的思想设计了Rho方法。假设找到碰撞 ga1hb1=ga2hb2, 从而 (b1-b2)x≡a2-a1(modN)。 如果gcd(b1,b2,N)=1,那么可以求解x。 为了能够以较低的空间找到所需的碰撞,Rho方法结合了伪随机游走和Floyd寻找碰撞的技术。Pollard将G划分成3个互不相交的集合G1,G2,G3。选定初始值s0=ga0hb0,定义如下伪随机游走序列si=gaihbi, 对应的可以得到(ai+1,bi+1)的迭代公式。为了找到碰撞sm=sn,m≠n,在第i步保存信息(si,ai,bi,s2i,a2i,b2i)并判断是否si=s2i。 研究者后续提出了针对Rho方法的许多改进,包括采用并行计算、群的划分以及使用其他形式的随机游走等。 2.5.2 Pollard袋鼠算法与Gaudry-Schost方法 针对小区间离散对数问题0≤x 在袋鼠算法中有2类游走,一类是家袋鼠游走gai,另一类是野袋鼠游走hgbi。与Rho方法中的游走类似的是,Lambda方法中袋鼠的游走是由现在的值所对应的分类决定;不同的是,步长按照预计算的一些小步决定。 Van Oorschot和Wiener使用了区分点技术来降低存储,王瑶等[33]通过将一次大整数乘法分解为多次小整数乘法提高运算效率。 针对高维离散对数问题,Gaudry等[34]用伪随机游走结合区分点的算法。 上述算法没有利用群的任何其他性质,因此,对所有抽象群都适用。 Bartusek等[39]指出在通用群模型下,群的生成元是固定的,或者是随机影响到离散对数问题和DH问题的求解下界。 根据上述结论可知,为降低算法复杂度的数量级,需要利用群的具体特性。注意到,离散对数满足如下等式: logg(h1h2)=logg(h1)+logg(h2)。 该性质启发我们求解离散对数的时候,不止需要考察元素本身,也需要考察元素的分解情况。如果能赋予群元素一种“大小”关系,并且能够用某种方法将“较大”元素表示成“较小”元素的乘积,那么就可以从“较小”元素的离散对数恢复出“较大”元素的离散对数。特别地,当群中的元素可以自然地看成(代数)整数或者有限域上的多项式时,可以用范数或多项式的次数来描述元素的大小关系。 上述思想已经体现在早期相关的工作中,并逐步发展完善,基于上述基本思想设计了指标计算框架,应用于整数分解、有限域和超椭圆曲线离散对数求解等。而对于椭圆曲线,目前暂未找到比较好的指标计算方法。 指标计算方法中的一个基本概念是(在合适范数下的)光滑性,其刻画一个“较大”元素是否能表示成一些“较小”元素的乘积。 指标计算框架一般包括如下3个部分: (1)确定因子基(也称光滑基)。根据具体的问题参数确定因子基S={s1,s2,…,sk}⊂G,例如,选定光滑界b之后所有b-光滑的元素添加g的集合。 (2)求解因子基元素离散对数。首先需要生成关系式,考察同态映射: φ:k→G, e11loggs1+…+e1kloggsk=0modN。 因此,通过关系式就得到了一个以因子基元素离散对数为变量的线性同余方程。 当收集到足够多的关系式,就可以求解线性同余方程组,得到因子(后面都统一成因子基)基元素的离散对数。 在实际求解过程中,所得到线性同余方程往往是稀疏的,可以采用比消元法更快的求解算法,如Wiedemann算法[43]。 (3)目标元素离散对数。给定目标元素h,为了求解这个元素的离散对数,可以通过一定的方法将该元素(可以是该元素的方幂)表示为因子基元素的组合。从而可以由因子基元素的离散对数推导出目标元素的离散对数。 有限域上的任意函数可以表示称为多项式的形式,特别地,有限域上的离散对数看作一个函数也有多项式表示[44-49],但是直接使用多项式计算离散对数的效率并不高。 针对有限域的具体表示,可以结合指标计算框架设计比通用求解算法更高效的方法,记 LQ(α,c)=exp((c+o(1))(logQ)α(loglogQ)1-α), 其中,0≤α≤1,c是一个常数,有时简记为LQ(α)或者L(α)。 令Q=pn表示有限域pn的元素个数,考虑当参数趋于无穷的情况,随着Q→∞特征p=LQ(αp,cp)。 如果αp>1/3,称为中等特征或大特征有限域,目前最快的求解算法是数域筛法[50-53],时间复杂度是亚指数时间;如果αp<1/3,称为小特征的情况,目前最快的求解算法渐进时间复杂度为准多项式时间[54-57]。 数域筛法是在指标计算框架的基础上,结合中等和大特征有限域的具体表示设计的,其将有限域提升到数域中,利用数域中元素的范数来确定元素的大小。数域筛法包括多项式选取、因子基离散对数求解和目标元素离散对数求解。设目标有限域为pn。 (1)在多项式选取阶段,需要选取2个整系数的不可约多项式f(x)和g(x),使得它们的模p有n次不可约公因式ψ(x)。这样可以得到上的2个数域Kf和Kg,如图1所示。 图1 数域构造Fig.1 Construction of number fields 图2 数域筛法Fig.2 The number field sieve 对于一个整系数多项式,可以分别将其看成Kf和Kg中的元素,并且通过有限域pn联系起来。 (2)在因子基元素离散对数阶段,需要根据具体参数选取合适的因子基,通过筛法求解出相应的离散对数。 由于数域中只存在素理想的唯一分解,因此,取因子基为一些范数较小的素理想。这里以筛1次多项式为例,此时取因子基为范数不超过B的1次素理想。 在给定范围内筛(a,b)对,希望多项式a+bx在Kf和Kg中同时B-光滑,即a+bx在Kf和Kg中生成的主理想能同时分解成因子基中素理想的乘积。这样便得到了因子基元素之间的一个同余方程。接着利用λ映射[51],将素理想之间的关系方程转化成元素之间的关系方程。当得到足够多的关系方程后,通过解方程便可得到因子基元素的离散对数。 需要注意的是,对于中等特征有限域,通常筛1次多项式是不够的,还需要筛高次多项式。此时因子基也需要包含相应的高次素理想。 (3)在目标元素离散对数求解阶段,需要在前2步的基础上求解给定的目标元素离散对数。这一步又可以分为2个阶段:光滑化阶段和递降阶段。 在光滑化阶段,通过将目标元素随机化,期待其较为光滑,即希望目标元素能分解成若干范数较小的元素。在递降阶段,将上述范数较小的元素通过格筛的方法进一步降低其范数,使其归约到因子基元素中,从而恢复出对应的离散对数。 数域筛法的渐进复杂度为L(1/3,c),在实际使用中,计算因子基离散对数是其最耗时的部分。目前,数域筛法的改进均集中在第二个参数c上。 由于数域定义多项式的性质将影响被筛元素的光滑概率,从而影响算法的复杂度,研究者提出了多种不同的多项式选取方法[52,58-60]。特别地,当有限域的特征满足某些特定条件时,可以构造出性质更好的多项式,这类方法称为特殊数域筛法[61-62]。 有别于仅构造2个数域,研究者发现可以利用多个数域提高关系方程的收集效率,这类方法称为多重数域筛法[63-65]。 如果构造的数域具有非平凡的自同构,可以利用自同构将因子基中元素划分成等价类,从而减少所需计算的因子基离散对数数目[52,59]。 当有限域的扩张次数大于1时,可以利用有限域的真子域构造范数较小的等价元素,以提高目标元素的光滑概率,从而降低光滑化阶段的复杂度[67-69]。 在递降阶段,除了常用的一次素理想外,也可以使用高次素理想来提高计算效率[69-70]。 目前,计算素域中离散对数的记录由Boudot等[71]保持,他们使用数域筛法计算了整数模795比特安全素数的素域中的离散对数问题。值得注意的是,Fried等[72]在此之前计算了1 024比特素域中的离散对数,不过这里选取的素域适用于特殊数域筛法,并且其有160比特的子群。 早期求解小特征有限域离散对数较快的算法是在指标计算框架基础上发展出的函数域筛法[73-76]。函数域筛法与数域筛法类似,只不过将有限域提升到函数域,用多项式的次数代替之前数域中元素的范数来确定元素的大小。 原始的函数域筛法过于技术性,Joux等[76]在2006年给出了简化版本。算法的框架如图3所示: 图3 函数域筛法Fig.3 The function field sieve 函数域筛法的流程与数域筛法类似,不同的是,此时处理对象是函数域中的多项式而不是数域中的代数整数,这里省略算法细节。 在2013年,Joux[77]提出了小特征有限域的Frobenius表示,并且提出了复杂度为L(1/4)的求解算法。此后又进一步改进得到准多项式时间的BGJT算法。 (1)构造有限域的Frobenius表示。为此,需要将给定的有限域嵌入到合适的扩域: pk → qk → q2k , 这里,q=pr,r=「logpk⎤。 搜索低次数多项式h0,h1∈q2[x] 使得存在不可约因子: f(x)|h1(x)xq-h0(x), 其中,f(x)∈q2[x],并且deg(f(x))=k。 该性质有利于提高后续产生关系式的效率。但是,Cheng等[78]指出采用这种表示本质上是在剩余类环q2[x]/(h1(x)xq-h0(x))上做运算,需要处理零因子的影响。 (2)假设选取相对于ζ次数为1的有限域元素为因子基元素。为了求解因子基元素的离散对数,注意到有恒等式: 应用Mobius 变换 x 去掉分母后得到 (cζ+d)(aζ+b)q)-(aζ+b)(cζ+d)q。 根据q-次方幂的性质得到 (cζ+d)(aqζq+bq)-(aζ+b)(cqζq+dq)。 根据构造有ζq=h0(ζ)/h1(ζ),带入上式得 (aqh0(ζ)+bqh1(ζ))(cζ+d)- (aζ+b)(cqh0(ζ)+dqh1(ζ))。 注意到上式2边相对于ζ的次数都不高,因此有较高的概率2边都分裂成一次元素的乘积。 为了得到不同的关系式,需要选取子群PGL(2,q) 在群PGL(2,q2)中不同陪集的代表元[79]。 (3)假设目标元素是W(ζ)∈q2k[ζ],W相对于ζ的次数大于1。 类似地,考虑恒等式: 然后应用变量替换 x 带入并展开后可得左边是W相关的元素乘积,如果右边是deg(W)/2光滑的,就得到一个关系式。收集到足够多的关系式之后,可以将W约化到deg(W)/2光滑的元素。通过迭代,可以归约到因子基元素的离散对数。 针对小特征有限域离散对数时间复杂度较低的求解算法有的依赖于一些启发式假设,一些改进工作旨在探索是否可以减少或者替换启发式假设,比如概率算法[57]和确定性算法[80]。 目前,小特征有限域离散对数的计算记录由Granger等[81]保持,他们求解了30 750比特二元域中的离散对数。 其中,q+1-NE称为E的迹。 针对一般的椭圆曲线离散对数问题,目前通用求解方法仍是最优的计算椭圆曲线离散对数的方法。为了减少空间复杂度,经常采用的是基于伪随机游走的方法,例如,Pollard方法和Gaudry-Schost方法等。李俊全等[84]研究了迭代函数的设计准则,并且给出了一个改进的并行碰撞算法。 但是结合椭圆曲线的性质,可以做一些改进。例如,Gallant等[85]和Wiener等[86]提出利用自同构将群元素划分成等价类,从而提高算法效率。Galbraith等[87]利用椭圆曲线易于求逆的性质对区间离散对数求解进行加速,Zhu等[88]在此基础上进一步做出了改进。Zhang等[89]用二元域上椭圆曲线的半点运算比倍点运算更快的特点加速离散对数的求解。Wu等[90]给出了Gaudry-Schost算法的一个渐近时间复杂度最优的改进. 5.2.1 归约到有限域乘法群 Meneze等[91]和Frey等[92]利用双线性映射工具提出了一种约化方法,将椭圆曲线离散对数问题归约到有限域的适当扩域qk上的离散对数问题,然后利用计算有限域离散对数的更高效的求解方法。这里的k称为曲线的嵌入次数,其通常很大,因此该方法仅对少数曲线有效。特别地,当曲线的迹被p整除时,这类曲线称为超奇异椭圆曲线,其嵌入次数不超过6,极易受到这类方法攻击。 针对特殊的参数,文献[93-94]考察了有限域离散对数问题和椭圆曲线离散对数问题的关系。 5.2.2 归约到有限域加法群 如果椭圆曲线满足NE=q,即迹为1,称为异常椭圆曲线。特别地,当q=p为素数时,这类曲线的点群恰好是素数阶的,似乎满足密码学的要求。但是异常椭圆曲线离散对数问题却是十分容易的,Smart[95]、Satoh等[96]、Semaev[97]分别独立给出了高效求解算法。前2者是一种提升方法,针对素域的情形,将曲线提升到p进数域p中,利用形式对数将椭圆曲线的点群归约成有限域的加法群。之后朱玉清等[98]拓展了提升方法的使用范围,可以求解一般有限域上椭圆曲线p-群中的离散对数问题。Semaev则是利用除子和微分形式空间的对应,在固定点的取值将椭圆曲线离散对数问题归约成有限域加法群中的离散对数问题。之后祝跃飞等[99]对其进行优化,给出了在无穷远点取值的方法,避免了在扩域上进行运算。 在椭圆曲线上直接设计指标计算法并不容易(见下一小节),但对于亏格g≥2的光滑代数曲线C,存在指标计算法可以有效地计算其雅可比Jac(C)中的离散对数。当曲线是超椭圆曲线时,由于其雅可比中元素存在Mumford表示,即表示成2个次数较低的多项式,利用多项式的分解性质可以给出亚指数时间的指标计算法[100]。对于一般曲线,研究者利用“双大素数”技巧给出了时间复杂度为O(q2-2/g)的算法,即使对于较小的亏格g,其效率也优于Pollard rho算法[101-102]。 为了利用上述指标计算法,自然的想法是将椭圆曲线离散对数归约成代数曲线雅可比中的离散对数。为此,Frey等[103]提出了Weil下降方法,之后Galbraith等[104]对其进行了完善。 设E是定义在扩域qn上的椭圆曲线,曲线方程为f(X,Y)=0。取qn关于q的一组基{1,θ,θ2,…,θn-1},令 X=X0+X1θ+…+Xn-1θn-1,Y=Y0+Y1θ+…+Yn-1θn-1, 则f(X,Y)=0可以表示成 ∑fi(X0,…,Xn-1,Y0,…,Yn-1)θi=0, 其中,fi是q上多项式。通过这种方式,可以由qn的椭圆曲线得到q上的n维阿贝尔簇。如果能找到一条曲线C使得其雅可比Jac(C)包含该阿贝尔簇,则能将椭圆曲线的离散对数问题归约成Jac(C)中的离散对数问题,再利用指标计算法求解。 对于特征2有限域,Gaudry等[105]利用函数域的Artin-Schreier扩张构造了满足条件的曲线,之后Diem[106]用Kummer扩张给出了奇特征情形的构造方式,这类构造方法统称为GHS攻击。该攻击对一些曲线取得了比较好的效果,但是对于大部分椭圆曲线而言,该方法得到的覆盖曲线的亏格很高,其关于n是指数级的,导致效率并不比通用算法高。 仿照第3节指标计算法的框架,椭圆曲线离散对数的指标计算流程如下:取定E(q)的某个子集为因子基;选取随机的点R=aP+bQ,将其分解成因子基中点的和,即aP+bQ=∑eiPi,其中,Pi为因子基中元素;收集足够多这样的关系式,从而计算出Q关于P的离散对数。 对于有限域中的元素,其可以自然地提升到数域或者函数域,根据素理想或者多项式的唯一分解性可以分解成一些范数小或者次数低的元素。而对于椭圆曲线,如何定义因子基并给出有效的点分解算法是设计椭圆曲线指标计算法的难点所在。为此,Semaev[107]提出了求和多项式。 (x1,y1)+(x2,y2)+…+(xm,ym)=O, 对于素域上的椭圆曲线,一般取因子基为x坐标小于预先取定的正整数B的有理点全体。此时,为了得到点R=(xR,yR)与因子基元素的关系式,可以计算Sm(X1,X2,…,Xm-1,xR)=0中小于B的零点。若该方程存在零点,则说明可以找到点R与m-1个因子基元素的关系式。对于扩域qn上的椭圆曲线,Gaudry[108]和Diem[109]取因子基为x坐标落在qn的某个q子空间中的有理点全体。通过对Sm=0使用Weil限制,可以将qn上的方程转换成子域q上n个代数方程,从而更易于计算。 然而计算上述代数方程(组)的零点通常并不容易,一般均需使用Gröbner基算法,算法的时间复杂度为O(Nd),其中,N为变量个数,d为正则次数。研究表明,这类方程的正则次数通常很高[110-111]。 为了提高求解求和多项式零点的效率,研究者尝试利用求和多项式的对称性降低多项式的次数[112-113],将求和多项式分裂成多个子求和多项式组,通过增加变量数目降低方程次数[114],以及利用Frobenius映射加速方程的求解[115]。1.3 离散对数问题扩展
2 通用求解算法
2.1 随机自归约和比特困难性
2.2 量子算法
2.3 Pohlig-Hellman方法
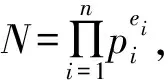
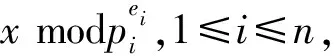
2.4 小步-大步法
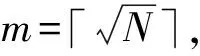
2.5 低存储的概率算法

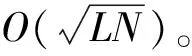
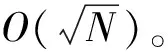
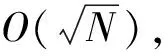
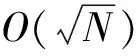
2.6 一般群模型和计算下界

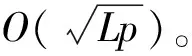
3 指标计算框架
3.1 光滑性和概率
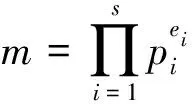
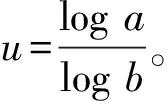
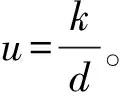
3.2 指标计算框架
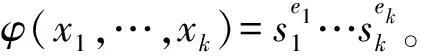
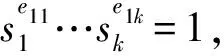
4 有限域离散对数求解
4.1 有限域按照特征的分类
4.2 中等和大特征有限域离散对数

4.3 小特征有限域离散对数

5 椭圆曲线离散对数求解
5.1 一般椭圆曲线
5.2 归约到有限域
5.3 归约到高亏格曲线
5.4 基于求和多项式的指标计算法