基于极化通道扩展与盲源分离的雷达主瓣复合拖引干扰对抗方法*

原 慧，李军涛，安 磊，宫 健

（1.中国人民解放军94221部队，山东 日照276800；2.空军工程大学防空反导学院，陕西 西安710051）

0 引言

现代相控阵雷达普遍具有多目标探测和跟踪能力，所以目前的自卫式拖引干扰通常与具有压制效果的干扰信号进行复合，形成“雷达主瓣复合拖引干扰”，以达到“隐真示假”的干扰目的。这样，早期的边沿跟踪、距离保护波门、宽波门跟踪、记忆波门跟踪等波门跟踪策略[1]将失效。而其它现有基于目标和干扰信号幅度特征差异的干扰检测方法[2-4]、利用数字射频存储(DRFM)转发式干扰机的非理想转发干扰特征进行干扰信号的检测、识别与抑制的方法[5-6]、利用空时自适应和极化信息处理等方法对干扰进行检测、识别与抑制的方法[7]以及其它一些信号或数据处理的干扰抑制方法，都没有考虑复合干扰的情况，仅仅针对单独的拖引干扰展开研究。因此，迫切需要开展针对雷达主瓣复合拖引干扰对抗方法的研究。

1 雷达主瓣复合拖引干扰信号建模

假设拖引干扰为jd(t)，下标d代表deceive(欺骗)，具有压制效果的干扰信号为jb(t)，下标b代表blanketing(遮盖)，则自卫式复合拖引干扰信号可以表示为：

式中，jb(t)可以是噪声调频、噪声卷积/乘积、频谱弥散(SMSP)干扰以及一定参数条件下的间歇采样转发干扰（ISRJ）等；η表示jd(t)和jb(t)的能量分配关系，η越大，压制效果越明显，为不失一般性，以下分析仿真中均取η=1；拖引干扰jd(t)根据雷达发射信号的不同而不同。

雷达发射线性调频(LFM)信号时，jd(t)通常为距离拖引干扰，根据LFM信号模型以及距离拖引干扰定义可以得到其具体的信号模型为：

式中，R(t)为目标相对于雷达的距离随时间的变化函数，v f为干扰进行匀速拖引时的拖引速度，af为干扰进行加速拖引时的拖引加速度，v f和af都可正可负，取正表示后拖，取负表示前拖。0≤t≤t1为停拖期，此时干扰完全与目标重合，但具有较强的干扰功率，从而取得对AGC的控制权；t1≤t≤t2为拖引期，此时假目标匀速或加速离开真实目标，距离波门跟随功率较强的假目标移动，经过一段时间后真实目标与距离波门分离；t2≤t时干扰关闭，距离波门内的假目标突然消失，跟踪环路失锁，迫使雷达重新转入对目标的搜索。雷达工作于脉冲多普勒(PD)体制时，jd(t)通常为距离-速度同步拖引干扰。现代PD雷达兼具距离和速度测量能力，可以同时获得目标的距离-速度二维信息，因此单独的距离或者速度波门拖引干扰对其干扰效果有限。为不失一般性，假设PD雷达发射单载频相干脉冲串信号，其信号模型可以表示如下：

基于DRFM干扰机的距离-速度同步拖引干扰的行程过程为：首先，对接收到的雷达发射信号进行下变频得到基带信号；然后，对基带信号进行相位量化模数转换并存储；最后，对存储在DRFM中的信号进行延时调制c(t)和多普勒频率调制b(t)后进行上变频并转发，形成对雷达的距离-速度同步拖引干扰(忽略初始相位项的影响)，则距离-速度同步拖引干扰的信号模型可以表示如下：

式中，fd为目标多普勒频率；对比式（3）中的拖引阶段，距离拖引时延函数c(t)=2vf t/c或af t2/c；为了实现同步干扰，同步施加的多普勒频率b(t)应满足：

此外，实际中，距离拖引通常在几秒时间内拖动几个距离波门宽度(μs量级)，因此，在一个PD雷达相关处理间隔(CPI)内，c(t)通常远小于T r，可以用δ(tnT r)代替式（5）中的δ(t-nT r-c(t))。则距离-速度同步拖引干扰信号模型可以简化为：

2 极化通道扩展建模

自卫式复合拖引干扰条件下，雷达只能接收到一路信号。雷达辅助天线通常用于相干旁瓣对消，在旁瓣对消系统中，为了消除主辅通道交叉极化响应不匹配的影响，辅助天线通常采用垂直和水平2种辅助天线以便对消掉干扰信号的垂直和水平分量。那么，这里就可以利用与主天线极化方式正交的辅助天线接收信号，构建第2路混叠信号，得到进入雷达主、辅天线的接收信号vm(t)、va(t)：

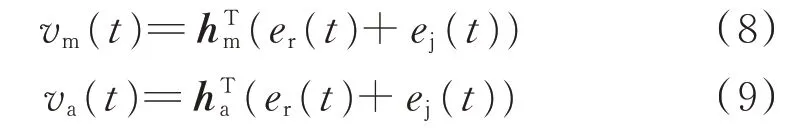
式中，hm为雷达主天线的极化矢量；ha为交叉极化辅助天线的极化矢量；er(t)、ej(t)分别表示在雷达接收天线端口处的目标回波信号和干扰信号，可分别表示为：

式中，Sp为目标的极化散射矩阵；hj为干扰机发射天线的极化矢量；Ar和Aj分别为雷达接收到的目标回波以及干扰信号的幅度。根据雷达方程和干扰方程，有：

式中，Pt为雷达发射信号的峰值功率；gm为雷达主天线增益；λ为雷达工作波长；σ为目标RCS；R为目标与雷达的距离。

考虑通道噪声N，并结合式（8）-（11），可以得到雷达主、辅接收通道信号的向量-矩阵表达式：

3 复值盲源分离算法——去噪CMN算法

负熵最大化(CMN)算法是经典的复值盲分离算法[8-9]，采用负熵度量分离信号之间的独立性，并利用非线性函数来近似负熵。CMN的代价函数为：

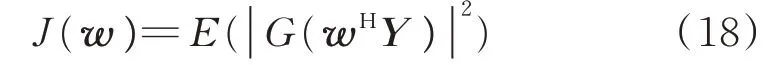
式中，CMN的代价函数包含了相位信息，从而能够比较灵活的对信源的概率密度进行匹配；w∈CN（N为快拍数）为分离矩阵的某一列，其满足约束条件阵。对观测数据按行去中心化后计算其协方差矩阵，并对其进行特征值分解后得到特征值组成的对角矩阵D=diag(λ1,λ2)以及对应的特征向量构成的特征向量矩阵

CMN的最优化问题可以表示成如下形式：

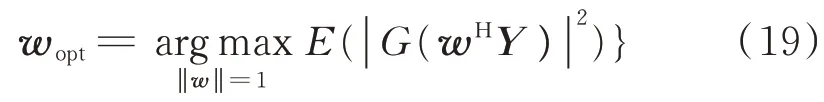
对于CMN，其非线性函数G也有多种选择：G1(u)=asinh(u)=lg(u+(1+u2)1/2)，G2(u)=cosh(u)=(eu+e-u)/2，G3(u)=ua(a＞0)，通 常 取a=1.25。相比基于G2和G3的算法，基于G1的算法更容易收敛到非理想解[8-9]。

基于牛顿法，可以推导出CMN算法分离矩阵每一列的更新表达式[8，10]：

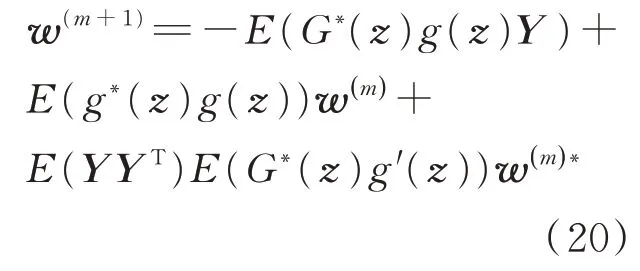
式（20）针对的是无噪或噪声很小可以忽略的盲源分离模型，因此式（20）等号右边第二项中用到了近似项E(YYH)=I，但当噪声较大不可忽略时，E(YYH)≠I，对式（20）进行如下修正，得到去噪CMN算法的固定点迭代公式为[9，11]：

4 仿真实验及分析

实验1：雷达发射LFM信号，自卫式干扰机采用噪声调频+距离拖引的复合干扰方式。

雷达及目标的相关参数设置如表1所示。

表1 相关参数设置

自卫式干扰机释放线性距离拖引干扰，拖引速度约为200 m/s。仿真中忽略了目标在不同极化状态下的RCS变化，并且假设主、辅接收通道的通道噪声相互统计独立，为服从零均值、方差为σ2n的复高斯白噪声。

假设目标回波信号幅度为1，JSR=20 dB，SNR=10 dB，拖引期某时刻，拖引干扰将目标拖离600 m，图1给出了此时雷达接收到的目标回波信号与噪声调频+距离拖引复合干扰信号的时域波形及脉冲压缩结果，图2为分离信号的脉压结果。

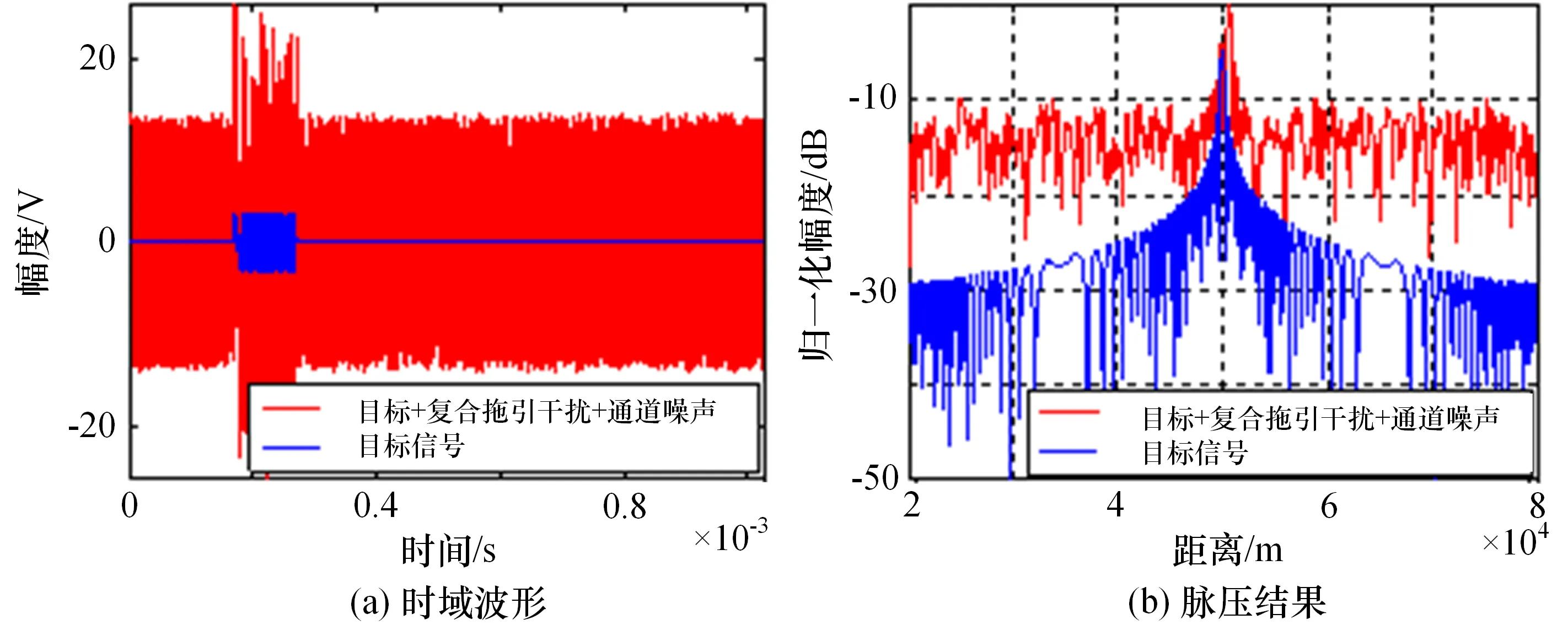
图1 噪声调频+距离拖引复合干扰条件下，雷达接收信号的时域波形及脉压结果

由图2可以看出，利用极化通道扩展+去噪CMN算法可以很好地将干扰信号与目标信号分离开。

图2 噪声调频+距离拖引复合干扰条件下，分离信号的脉压结果

当SNR从-10 d B以步长5 d B变化到15 d B，JSR从10 dB以步长5 dB变化到30 dB时，表2给出了复合干扰条件下的分离性能10 lg IA(Amari指数)。

从表2可以看出，在较广范围的SNR和JSR条件下，基于极化通道扩展+去噪CMN算法的信号分离性能都可以达到-20 d B左右，说明分离性能非常好。利用分离出来的2路信号就可以对目标和干扰进行同时跟踪处理，而不会将目标信号丢失。

表2 不同条件下的分离性能10 lg I A dB

实验2：雷达发射相干脉冲串信号，自卫式干扰机采用噪声调频+距离-速度同步拖引的复合干扰方式。

仿真实验参数如表3所示，雷达及干扰的天线极化方式、目标极化散射矩阵与实验1相同。

根据表3中参数可以计算得到拖引率为α=β/T c≈10-6，为了实现同步干扰，施加的多普勒频率应为fdj=2αf0=19.31 k Hz。

表3 仿真实验相关参数

假设目标回波信号幅度为1，JSR=20 d B，SNR=10 dB，图3给出了雷达接收到的目标+复合拖引干扰信号的时域及频域波形。

图3 噪声调频+距离-速度同步拖引复合干扰条件下，雷达接收信号的时、频域波形

由图3（b）可以看出，真、假目标的多普勒频率相差约19.39 k Hz，与理论值基本一致，误差是计算机量化造成的。利用上节提出的极化通道扩展+去噪CMN算法，可以得到2路分离的信号，图4给出了2路分离信号的幅频分布。

由图4可以看出，利用极化通道扩展+去噪CMN算法可以很好地将干扰信号与目标信号分离开。

图4 噪声调频+距离-速度同步拖引复合干扰条件下，分离信号的频域波形

当SNR从-10 dB以步长5 dB变化到15 dB，JSR从10 dB以步长5 d B变化到30 d B时，利用极化通道扩展+去噪CMN算法分离信号的分离性能结果与表2近似，也都可以达到-20 dB左右，说明利用本文所提出的方法可以很好地分离目标与复合拖引干扰信号，进而可以利用分离出来的2路信号完成对目标和干扰的同时跟踪处理，而不会丢失目标信号。

5 结束语

自卫式压制+拖引复合干扰可以在雷达的跟踪过程中达到“隐真示假”的干扰目的，且由于干扰信号与目标信号来自同一方向，雷达接收到的为一单通道信号，传统正定或者超定盲源分离算法无法解决此问题。基于此问题，本文提出了一种极化通道扩展与盲源分离结合的干扰抑制方法：首先，通过极化通道扩展将单通道信号扩展为双通道信号；然后，利用去噪CMN算法进行目标与干扰信号的分离，完成对目标和干扰信号的同时重构。仿真实验结果表明，在较广范围内的SNR和JSR条件下，所提方法都可以得到较好的分离性能，从而可以完成对目标和拖引干扰的同时跟踪，不会丢失目标。