建立城市坐标系的关键问题探讨*
2022-01-19朱月恒
马 波,张 洪,朱月恒
(云南省地矿测绘院,云南 昆明 650218)
0 引言
随着改革开放的不断深化,中国的政治建设、经济建设、文化建设、基础设施建设、网络建设以及城市化进程等领域经历了40多年的高速发展。在城市建设领域,大部分城市的国土部门和规划部门都先后建立了各自体系内的城市坐标系,以满足其相关业务的顺利开展。目前,随着自然资源局的挂牌成立,原国土和规划部门的并入,坐标系的不一致、原有基础资料的共享利用、相关业务是否能顺利开展成为了急待解决的问题。
我国西部地区的海拔较高,属于高原地区,采用国家大地坐标系(CGCS2000)投影至椭球体面上的坐标不能满足长度变形值不大于25 mm/km的要求(CJJ/T 8—2011《城市测量规范》中的基本规定第一条要求:城市平面坐标系的投影长度变形值不应大于25 mm/km)[2],需要将控制网边长投影至某一高程面上,建立相对独立的城市坐标系。
在不考虑高斯投影变形的前提下,简化后的每千米高程投影变形公式为:
(1)
式中:H为大地高;R为CGCS2000框架下地球椭球的平均曲率半径。
通过式(1)计算可得表1结果。
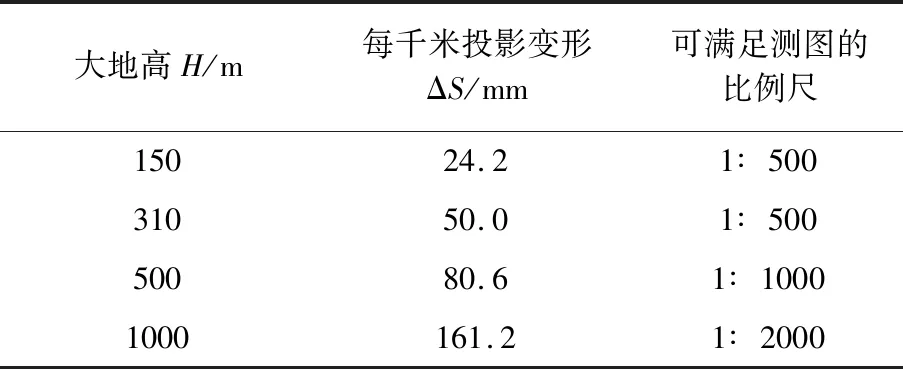
表1 投影变形对比表Tab.1 Comparison of projection deformation
从表1可以看出:对于海拔高高于150 m的城市,不能直接采用国家大地坐标系作为城市坐标系,必须建立与国家大地坐标系有关联的城市独立坐标系,以满足城市建设中规划、设计、施工、验收、变形监测等需要。建立独立坐标系时,可根据城市所在地理位置、海拔高度、投影变形值等因素综合考虑中央子午线经度和抵偿高程面高程值。
1 中央子午线和抵偿高程面的选取
1.1 任意3度带抵偿面高斯投影坐标系
从式(1)可知,高程投影变形值恒为负数,通过高斯投影公式可知高斯投影变形值恒为正数,故二者可相互抵消,建立城市坐标系宜采用“任意3度带抵偿面高斯投影坐标系”[2-5]。
通常情况下,选择城市中心作为中央子午线位置,选择平均海拔高程作为抵偿高程面高程。但是,根据笔者多年的工作经验和大量的实践证明,如不进行严密的公式推导和计算以及大量算例数据的验证,就确定中央子午线经度和抵偿高程面的值,是不可取的。中央子午线和抵偿高程面的选择需要结合城市的地形地貌及建设发展情况,通过严密公式精确计算出不同地理位置的投影变形值,并综合考虑抵偿高程面与偏离中央子午线Y坐标的关系式,最终确定中央子午线经度和主投影面高程,达到利用一个投影面控制面积最大化的要求。
1.2 投影变形
1.2.1 高程投影变形
如图1所示,可推导出各参考面边长与参考椭球半径、大地高、正常高、高程异常的关系。设地球表面观测所得边长为S,抵偿高程面边长为S0,Hm为大地高,H0为高程抵偿投影面的正常高,hm为参考椭球的高程异常,Δh为地面点高出抵偿投影面的高差,R为参考椭球的平均曲率半径。根据相似三角形原理,可得:
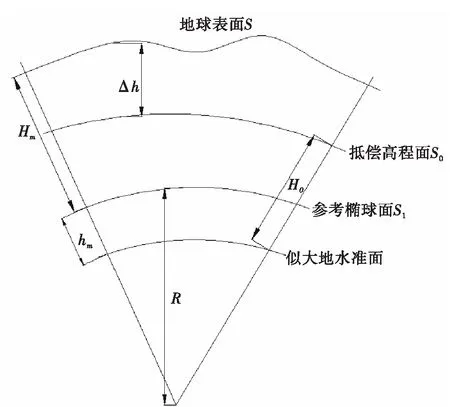
图1 椭球参考面关系图Fig.1 Relationship of ellipsoidal reference surface
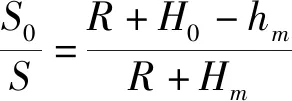
(2)
如图1所示,可得Hm=H0-hm+Δh。
由式(2)可推导出:
(3)
将式(3)按照牛顿二项式定理[3]进行展开,取至前四项,可得到毫米级精度的高程投影长度比公式,设高程投影长度比为m1,公式可写为:
(4)
1.2.2 高斯投影变形
本文要讨论的是球面坐标投影至高斯平面直角坐标后的投影变形情况,并推导出高斯投影长度比公式。可通过高斯投影正算公式推导出高斯投影长度比公式。
高斯投影正算公式中的第二式[4]:

cos5B(5-18t2+t4+14η2-58η2t2)l″5
(5)
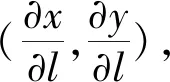
(6)
式(6)即为高斯投影长度比公式,其中,ym为两点间的Y坐标平均值,Δy为两点间的Y坐标差值,R为平均曲率半径。
1.2.3 投影变形公式
某一椭球面上的边长经高程投影和高斯投影至高斯平面上,其边长投影长度比为:
(7)
投影后的长度变形为(1-m1×m2);按《城市测量规范》的要求,投影后长度变形要求满足“每公里变形不大于±25 mm”,令式(7)的右边为“±25”,式(7)的左边为“投影长度变形×1 000 000”,即可得到每千米边长的投影变形公式:
(1-m1×m2)×1 000 000=±25
(8)
可以看出式(8)是一个以Δh和ym为变化量的二元函数,Δh为高出抵偿面的高差,ym为偏离中央子午线Y坐标值,为了方便研究式(8)的性质和图像,m1、m2只取其第一项,即可得到边长投影长度变形公式的简化公式,即:
(9)
式中:R、H0、hm均为常数,设(R+H0-hm)=B,2R2=C;则式(9)可写为:
(10)
以CGCS2000地球椭球为例,椭球平均曲率半径R=6 202 279 m,由于高程抵偿面H0和参考椭球高程异常hm两个数值涉密,故在此不列出具体值,直接代入计算,可得式(10)中B=6 204 100 m,C=2R2=7.693 652 95913m。将B、C的值代入式(10),可得到以Δh和ym为变化量、投影变形值为±25 mm的投影变形公式。
1.3 投影变形曲线图
为了进一步研究式(10)的图像及性质,在此定义坐标轴。以Δh变化的方向为坐标纵轴,以ym变化的方向为坐标横轴。在此坐标轴下,取一些特征值,使之满足式(10),可绘制出变形值为±25 mm的投影变形曲线图,如图2所示。
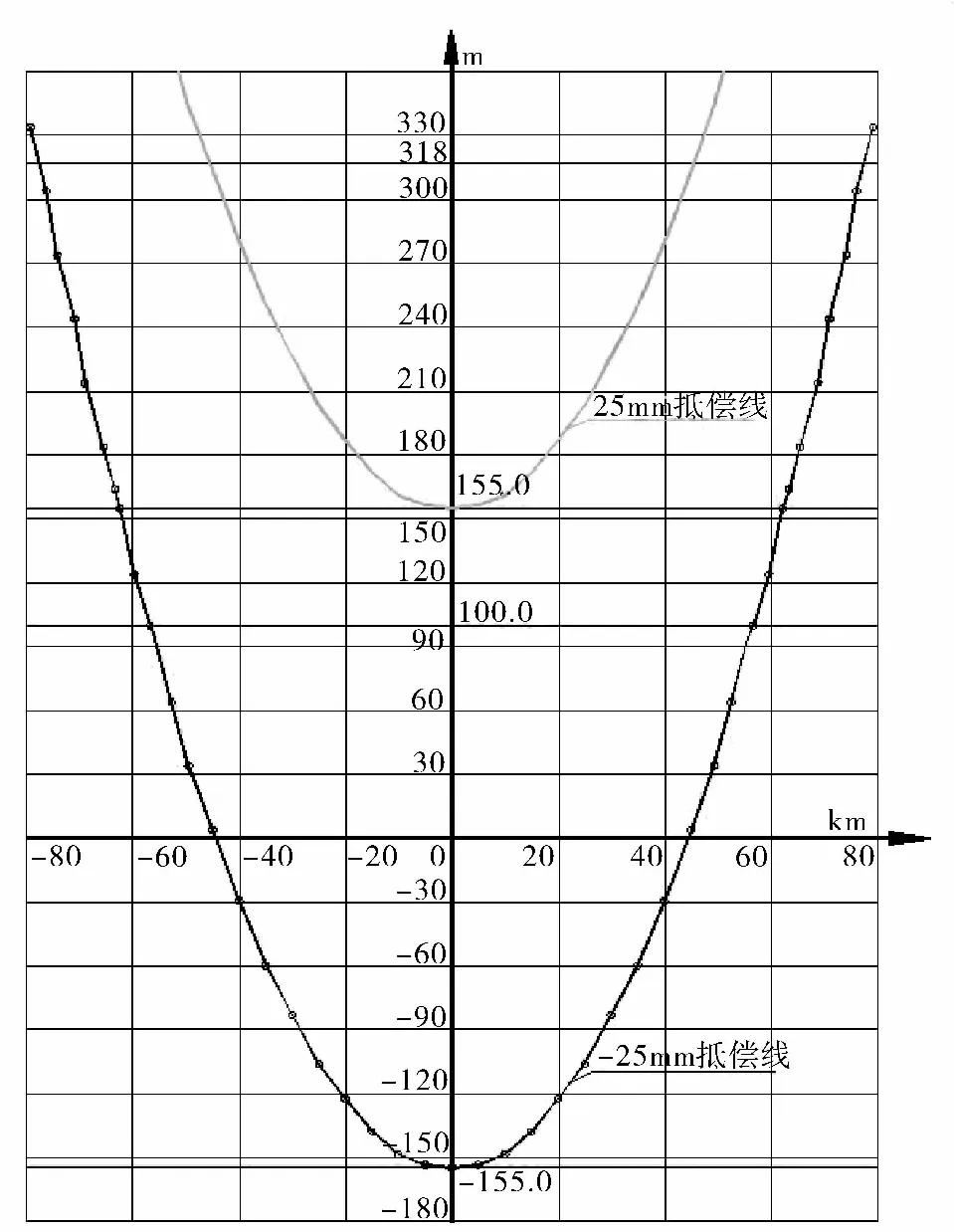
图2 投影变形曲线图Fig.2 Projection deformation curve
如图2所示,图中下方抛物线为“投影变形值为-25 mm”的曲线图,上方抛物线为“投影变形值为+25 mm”的曲线图。
综上所述,建立城市坐标系时,可根据图2的双曲线选取中央子午线经度和抵偿高程面高程,“中央子午线经度”应选取在城市中心位置偏西20 km左右,“抵偿高程面高程”应选取低于城市平均高程100 m至150 m;如需要精准到具体乡镇和位置,可提取Y坐标值和高程值,代入投影变形公式进行精确计算。如此反复选取和计算,可最终确定中央子午线经度和抵偿高程面高程,以及其控制的范围。
2 纵、横坐标加常数的选取
大地坐标转换为高斯投影坐标时,通常以赤道作为坐标横轴,中央子午线经线为坐标纵轴,由于中国处在北半球,投影后X坐标恒为正值,故X坐标的加常数一般设为 0 m;为了让Y坐标值不出现负数,Y坐标加常数一般设为500 km,这是一般的做法。
然而,根据笔者多年工作经验证明,如果城市坐标系也采用国家标准的坐标加常数,则两种坐标成果放在一起使用时,城市坐标系就没有一个较好的辨识度,也存在一定的用错坐标的隐患。为进一步说明此问题,给出如下算例:设T01点的大地经纬度分别为“25°01′46.25845″、102°47′52.10156″,经过3度带高斯投影后,不同坐标系的直角坐标如表2所示。

表2 国家标准坐标系成果表Tab.2 Results of national standard coordinate systems
从表2可看出,同一点的3种坐标系(1954年北京坐标系、1980西安坐标系、CGCS2000)坐标的相似度较高,一般技术人员在使用时比较容易混淆。假设所选取的中央子午线经度与标准3°带经线相差1°,经计算投影后的Y坐标大约相差“106 200 m”(按每秒29.5 m计算,此值根据椭球半轴近似计算可得);再经抵偿高程面投影改化后,其X坐标和Y坐标的变化值都不大;即各个坐标系高斯直角坐标值的辨识度不高。
综上所述,建议在建立城市坐标系时,高斯投影的纵、横坐标加常数都应考虑一个适当的数值,不应该(不用一刀切)采用与国家标准坐标系一样的处理方法(横坐标值加500 km);加常数的选取应充分考虑与其他坐标系(1954年北京坐标系、1980西安坐标系、CGCS2000)的辨识度,以便在使用过程中能够清晰、准确地辨认。
3 坐标成果的使用及坐标转换
城市坐标系一旦建立,并形成控制全市域范围的首级控制网,其控制网点的成果应形成一套完整的体系。即同一坐标系下,应具备3种不同形式的控制网点成果,且连同高程成果一并纳入。3种形式的坐标成果是:大地坐标(纬度B、经度L、大地高H),空间直角坐标(X、Y、Z),高斯投影直角坐标(X北坐标、Y东坐标、H正常高)。这3种坐标成果可通过高斯投影正、反算公式相互转换获得,此处不再累述。
在各个坐标系之间,为了获得严密的转换关系(参数),应采用七参数转换法,数学模型为布尔沙模型[1,5],计算公式为:
(11)
实践证明,如果控制点成果或地理信息数据的范围大于10 km2,应采用“布尔沙模型”的七参数转换法,才能够获得较高精度且分布均匀的转换参数。以下算例是150 km2范围的四等控制网,采用网内18个控制网点进行七参数和四参数计算;采用网内9个和网外6个同等级点进行精度检核。七参数转换法和四参数转换法的精度统计对比情况见表3-6。

表3 七参数转换法残差分布表Tab.3 Residual error distribution of seven-parameters conversion method
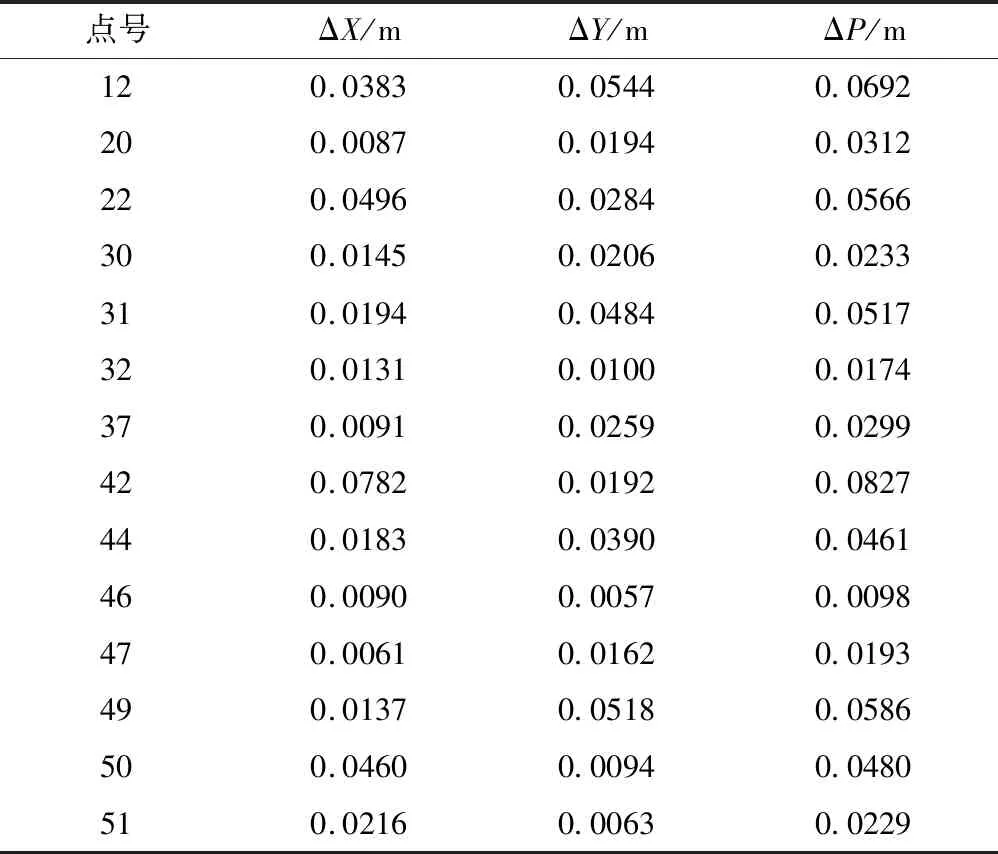
表4 四参数转换法残差分布表Tab.4 Residual error distribution of four-parameters conversion method
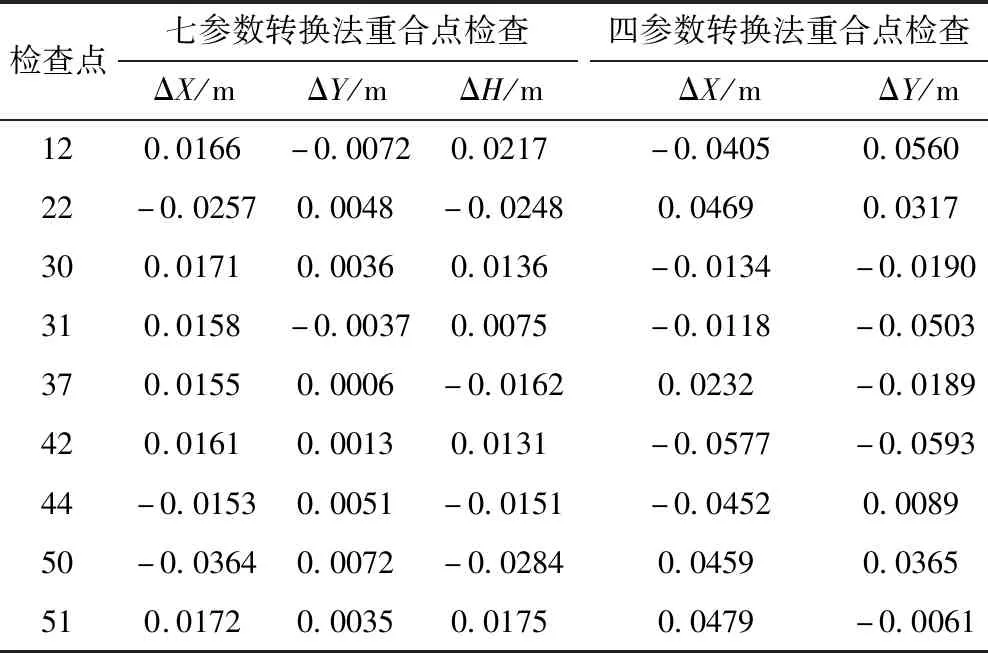
表5 内符合精度对比表Tab.5 Comparison of inside precision
经过以上算例的对比,可得出“布尔沙模型”的七参数转换法的优点:
1)转换精度较高、残差分布均匀;
2)具有高程拟合的效果,网内高程精度可达到“图根水准”的要求;
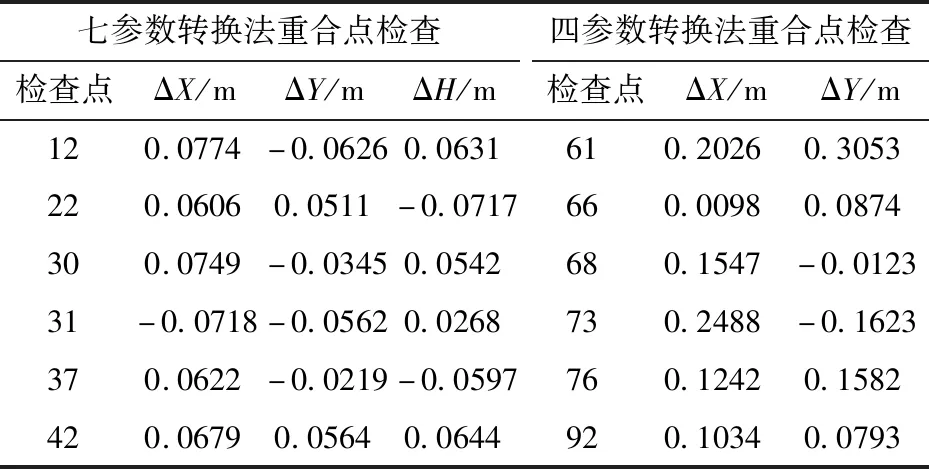
表6 外符合精度对比表Tab.6 Comparison of outside precision
3)根据外符合精度的分析,“布尔沙模型”的七参数转换法具有更高的稳定性。因此,对于大型(大面积)区域的坐标转换,建议采用“布尔沙模型”的七参数转换法。
4 结束语
本文通过公式推导和算例分析,旨在说明建立城市坐标系至少需要综合考虑3个方面的因素:中央子午线经度和抵偿高程面的选取;坐标加常数的目的和意义;坐标成果的使用及坐标系的转换问题。由此保证城市坐标系统的完整性、严密性和可靠性,这样在实际应用时才能获得高精度数据,成果也便于使用。
