基于不确定控制理论的最优策略研究
2022-01-19吴婉莹刘伟唐晓艺胡亦钧
吴婉莹, 刘伟, 唐晓艺, 胡亦钧
(1.新疆大学数学与系统科学学院, 新疆 乌鲁木齐830046;2.武汉大学数学与统计学院, 湖北 武汉 430072)
1.引言
许多学者对最优控制的研究主要在确定性的环境下进行, 即在确定性信息下建立最优控制模型.然而, 无论是在工程科技现象还是人文社会科学等各领域, 自然界存在大量不确定性现象.其中, 随机性是不确定性的一种基本类型, 使用概率论是解决这种不确定性现象强有力的工具之一.自上世纪七十年代以来, 随机最优控制理论己经成为现代控制理论的重要分支.随机最优控制理论在实际生活的诸多领域有着非常广泛的应用.Merton[1]研究了随机最优控制在经济学中的应用.Fleming和Rishel[2]等人描述了确定的以及随机最优控制理论.目前, 随机最优控制理论的相关研究仍是一个十分活跃的研究热点, 并且在金融研究领域方面发挥着越来越大的作用.
使用概率论对不确定性现象的研究中, 主要体现在概率分布函数, 通过抽取足够多的样本来描述不确定性事件的概率分布, 由概率分布刻画不确定现象.然而有时人们在许多情形下取不到足够多的样本做出有效的估计, 这使得人们很难获得准确的样本分布函数.LIU[3−4]提出了满足正规性、对偶性、次可加性和乘积测度公理的不确定性理论来刻画这种不确定性现象,其核心是利用不确定测度代替概率论中的概率, 解决不确定环境下不确定性问题.由不确定测度发展出来的控制模型, 称为不确定控制模型, 相关理论研究见文[5-7].本文采用文[3-4]中的观点来建立不确定控制问题.不确定最优控制问题所要研究的是, 选择最优的决策使得关于不确定过程的目标函数达到最优.但在不确定最优控制中, 由于控制系统的不确定性, 目标函数也具有不确定性, 因此不能直接把它看作实函数来研究.可以将问题转化成对不确定变量大小的比较, 对不确定变量去比较大小, 需在合理的数学意义下对不确定变量进行量化后再比较.事实上, 我们可以根据不同需要采取不同的判定准则, 例如, 期望值准则、乐观值准则、悲观值准则和Hurwize准则等.目前, 不确定性理论已成为公理化数学的一个分支, 它也被应用到金融领域, 见文[5-6,8-15].高建伟[16]在不确定理论框架下考虑了分别在固定缴费和不确定缴费下的固定缴费型养老金的投资策略问题.高建伟[17]考虑了一类带跳的养老金的不确定最优控制问题.现在利用不确定理论研究金融问题也成为了研究领域的一个热潮.
本文基于这种不确定性控制系统, 在乐观值准则下, 提出了一个带背景状态变量的不确定性最优控制模型.我们假设背景状态变量由一个不确定微分方程控制, 建立不确定性控制模型, 利用不确定性动态规划方法, 建立了最优性原理, 得到了最优性方程.最后, 讨论了一个DC型养老金计划的最优控制问题, 其中工资过程为相应的背景状态过程.通过求解不确定最优性方程得到了最优投资策略和最优支付率的显示解.
2.不确定理论的基础知识
首先给出一些基础知识.设Γ是一个非空集合,L是定义在Γ上的σ-代数.称每一个Λ ∈L为一个事件.
定义2.1[3]如果函数M且满足下列公理:
公理1(正规性) 对全集Γ, 有M{Γ}=1;
公理2(对偶性) 对任意事件Λ, 有M{Λ}+M{Λc}=1;
公理3(次可加性) 对于可数事件列{Λi}, 有
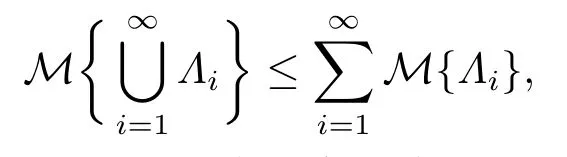
则称M为不确定测度, 并称三元组(Γ,L,M)为一个不确定空间.
公理4(乘积测度) 设(Γk,Lk,Mk) 是不确定空间, 而Mk是定义在其上的不确定测度,k=1,2,··· ,n, 则乘积不确定测度M是定义在乘积σ-代数L1×L2×···Ln上满足
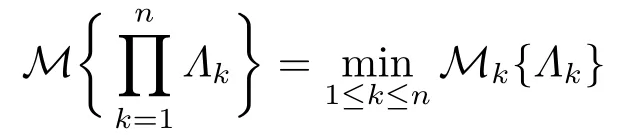
的不确定测度.
定义2.2[3]设ξ是从不确定空间(Γ,L,M)到实数集R的一个可测函数.如果对于任意的Borel集B, 集合
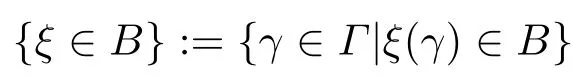
是一个事件, 则称ξ是一个不确定变量.
定义2.3[3]假设ξ1,ξ1,··· ,ξm是不确定变量, 如果对任意R中的Borel 集B1,B2,··· ,Bm,均有
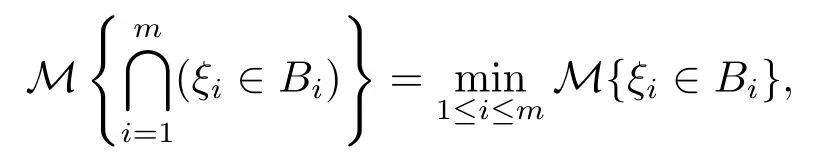
则称不确定变量ξ1,ξ1,··· ,ξm是相互独立的.
定义2.4[3]一个不确定变量ξ的不确定分布Φ: R→[0,1]是一个实函数, 对于任意的实数x满足:

定义2.5[3]设ξ是一个不确定变量, 如果下式中的两个积分至少有一个是有限的, 则ξ的期望值定义为:

ξ的方差定义为:

定义2.6[3]设T是指标集(比如:时间),(Γ,L,M)是一个不确定空间,Xt是从T×(Γ,L,M)到实数集的一个可测函数.如果对于任意的时间t ∈T和任意的Borel集B, 集合
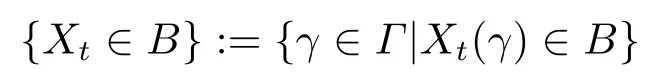
是L中的一个事件, 那么Xt是一个不确定过程.
定义2.7[9]设ξ为一个不确定变量, 并且α ∈(0,1],ξsup(α) := sup{r | M{ξ ≥r} ≥α}称为ξ的α-乐观值;ξinf(α):=inf{r |M{ξ ≤r}≥α}称为ξ的α-悲观值.
引理2.1[9]假定ξ和η都是不确定变量, 那么以下三式成立:
(i) 若λ ≥0, 那么(λξ)sup(α)=λξsup(α), 且(λξ)inf(α)=λξinf(α);
(ii) 若λ<0, 则(λξ)sup(α)=λξinf(α), 并且(λξ)inf(α)=λξsup(α);
(iii) (ξ+η)sup(α) =ξsup(α)+ηsup(α), (ξ+η)inf(α) =ξinf(α)+ηinf(α), 如果ξ和η相互独立.
定义2.8[9]设Ct是一个不确定过程, 如果它满足下面三个条件:
(i)C0=0, 几乎所有的样本路径是Lipschitz连续的;
(ii)Ct具有独立稳态增量;
(iii) 对于时间t, 增量Cs+t −Cs是一个期望值为0和方差为t2的正态不确定变量, 其不确定分布是

则称不确定过程Ct为典范Liu过程.
令Ct是一个典范Liu过程, 并且ξ= ΔCt=Ct+Δt −Ct.则对于任意的0< α ≤1,ξ的α-乐观值和α-悲观值分别是

和

引理2.2[9]设ξ是一个正态不确定变量N(0,σ),σ >0, 对于任意实数a, 任意足够小的ε>0和α ∈(0,1],
(i) 若b>0, 则
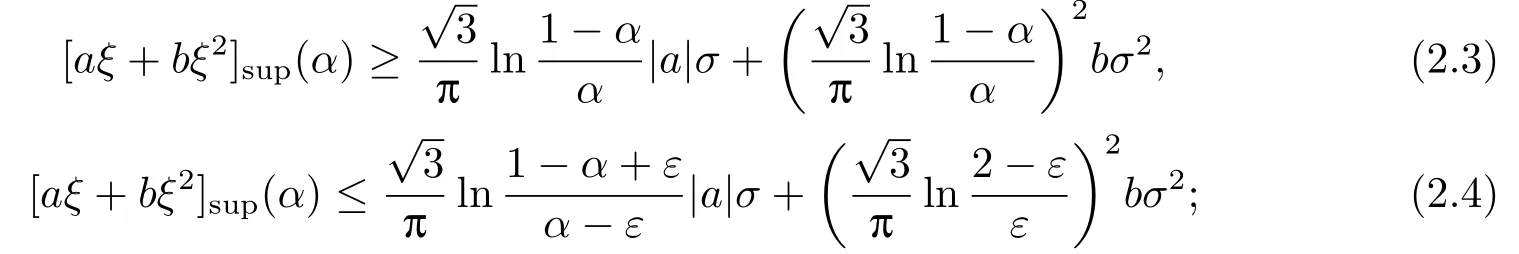
(ii) 若b<0, 则

(iii) 若b=0, 则

定义2.9[9]设Ct是一个典范Liu过程,g1和g2是两个给定的实函数,Xt是一个未知的不确定过程, 则称方程
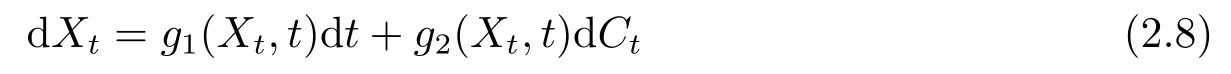
为一个由典范Liu过程驱动的不确定微分方程.它的解是满足(2.8)式的不确定过程.
引理2.3[9](基本定理) 设Ct是一个典范Liu过程,h(t,c)是一个连续可微的实函数, 则不确定过程Xt=h(t,Ct)是一个典范Liu过程, 且
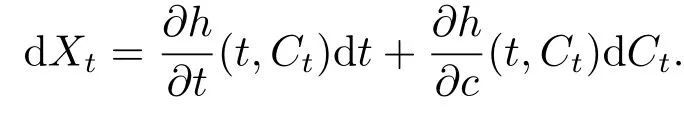
3.不确定最优控制的乐观值模型
在不确定最优控制问题中, 需要对包含不确定变量的目标函数进行优化, 并将不确定目标转化为确定的等价目标.在不确定最优控制中, 有很多准则: 期望值、乐观值、悲观值和Hurwicz 准则.本文讨论了一类包含背景状态变量的系统在乐观值准则下的最优控制问题.
假设Ct= (Ct1,Ct2,...,Ctk)T, 其中Ct1,Ct2,...,Ctk是相互独立的典范Liu过程.对任意的t ∈(0,T), 置信度α ∈(0,1], 研究如下的多维不确定乐观值最优控制问题:

其中,Xs是状态变量,Ls是背景状态变量,Dt是服从约束集D的控制变量.f: [0,T]×R×R×R→R 是目标函数,G: [0,T]×R×R→R 是终止收益函数.G(T,XT,LT)]sup(α) 是中括号里不确定变量的α-乐观值.另外,ν和λ是关于时间s, 状态Xs和背景状态Ls的两个函数.所有的函数都是连续的.为了求解该模型, 我们给出了以下最优性原理.
定理3.1(最优性原理) 对任意的(t,x,l)∈[0,T)×R×R, Δt>0且t+Δt 其中,x+ΔXt=Xt+Δt,l+ΔLt=Lt+Δt. 证用,x,l)表示(3.2)右边的式子, 则根据J(t,x,l)的定义有: 其中, 对任意的Ds,Ds|[t,t+Δt)和Ds|[t+Δt,T]是决策向量Ds分别在[t,t+Δt)和[t+Δt,T]上相应的取值. 对任意的Δt>0, 利用泰勒展开式, 我们有: 因此 对式(3.3)在Ds|[t+Δt,T]上取极大值, 我们有J(t,x,l)≥x,l). 另一方面, 对任意的Ds, 我们有: 因此, 我们得到J(t,x,l)≤¯J(t,x,l).根据式(3.3)和式(3.4), 得J(t,x,l)= ¯J(t,x,l).定理3.1 得证. 下面我们根据最优性原理给出带有背景状态变量的最优性方程. 定理3.2(最优性方程) 设J(t,x,l)在[0,T]×R×R上二次可微, 则 其中,Jt,Jx和Jl分别是J(t,x,l)对t,x和l的偏导数.f,ν,λ,Jt,Jx,Jl分别定义为f(t,x,l,Dt),ν(t,x,l,Dt),λ(t,x,l,Dt),Jt(t,x,l),Jx(t,x,l),Jl(t,x,l). 证对任意的Δt>0, 利用泰勒展开式, 我们得到: 其中,Jtt,Jxx,Jll,Jtx,Jtl,Jxl分别代表Jtt(t,x,l),Jxx(t,x,l),Jll(t,x,l),Jtx(t,x,l),Jtl(t,x,l),Jxl(t,x,l). 将式(3.6)代入式(3.2), 可得: 由模型(3.1)中的不确定微分方程可知: 将式(3.8)代入式(3.7), 可得: 其中, 1) 若q > 0, 由引理2.1中不等式(2.4)和上式(3.9), 对于Δt > 0, 若q > 0, 存在一个控制u ≡uε,Δt, 则 将不等式两边除以Δt, 我们得到: 当Δt →0 时, D(ε,Δt)→0, o(Δt)→0.令Δt →0, ε →0, 得到 同理, 由不等式(2.3)和式(3.9)可得 结合不等式(3.10)和(3.11), 得到 因此, q >0时, 式(3.5)成立. 2) 若q < 0, 由引理2.1中式(2.5), (2.6)可知, 式(3.5)可以采用与上述过程相似的方法进行证明. 3) 若q =0, 我们有 通过式(2.7), 同样可证得(3.5)成立. 因此, 定理3.2得证. 近年来, 由于养老金在金融市场和社会保障体系中发挥着至关重要的作用, 养老金管理已成为广大退休人员关注的重要课题.在固定缴费(DC)型养老金计划中, 投资风险与参与者的寿命风险由养老金管理者转移到了养老金参与者的身上, 从而DC型养老金计划更符合当今养老金体系的管理现状, 研究DC型养老金计划问题具有重要的理论意义和实践价值. 针对养老金问题, 传统的建模方法一般应用概率论对随机动态控制系统进行建模, 通过布朗运动描述金融市场的随机性, 利用动态规划方法研究了最优控制问题的动态系统.在不确定理论的框架下, 通过典范Liu过程刻画金融市场的不确定性, 运用动态规划法得到最优性方程,从而得到最优解. 假设养老金可以投资于无风险资产和服从收益为不确定过程的风险资产, 养老金的缴费与养老金成员的工资因素有关, 那么工资过程可以看作是DC型养老金计划控制问题中的背景状态过程, 建立不确定最优控制的乐观值模型. I 金融市场与财富过程 我们假设金融市场由两种资产组成, 一种是无风险资产, 即银行账户或债券, 另一种是单一风险资产, 即股票.无风险资产在t时刻的价格S0(t)服从不确定过程: 其中,r是常数, 代表利率. 从宏观经济学角度来讲, 风险资产和工资都受经济影响, 我们可以认为影响资产价格波动的宏观经济因素和影响工资波动的宏观经济因素是存在一定相关性的, 所以本文也为了计算的方便性, 不妨假设, 驱动风险资产价格过程的典范Liu过程与工资过程的典范Liu过程是同一个典范Liu过程.因此, 本文不确定性系统风险资产价格过程与工资过程模型如下: 风险资产在t时刻的价格S(t)服从以下不确定过程: 其中,µ是平均波动率,σ是风险资产的波动率,C(t)是一个典范Liu过程.一般我们假设µ>r. 定义t时刻的工资水平为L(t), 且L(t)服从不确定增长, 即 其中,µL为工资的期望收益率,σL为由风险资产波动导致工资变化的工资波动率,C(t)是一个典范Liu过程.假设θ是工资的比例, 养老金的缴费是以θL(t)连续地流入养老金账户. 假设养老金管理者可以分别投资于(4.1)和(4.2)所描述的无风险和风险资产, 并用该基金支付给养老金的退休成员.令x0表示基金的初始财富,ω(t)表示管理者在t时刻投资于风险资产的投资策略,B(t)表示在t时刻养老金的支付率,X(t)表示在t时刻养老金的财富, 于是养老金的财富过程遵循如下不确定微分方程: 利用式(4.1), (4.2)和(4.3), 我们可以重写式(4.4): II 最优化模型 我们假设基金的目标是选择最优投资策略ω(t)和最优支付率B(t), 使其二次损失函数的悲观值达到最小, 即得到如下不确定养老金问题: 其中,α1>0,α2>0,α1+α2= 1.置信水平为α ∈(0,1],ρ >0为折扣率, e−ρs为折现因子.bm为固定的目标缴费率,xp为固定的目标资金水平. 根据不确定动态规划理论, 可将值函数定义为: 由引理2.1可知, 模型(4.6)等价于下列模型(4.7), 问题转化为在乐观值准则下, 寻求目标函数的最大值. III 模型的求解 我们用不确定最优性方程来解出最优化问题(4.7)的显性解.根据定理3.2给出的不确定最优性方程, 有 其中,H(ω(t),B(t))代表花括号中的项. 现在求解式(4.8). 1) 若σLlJl+(σω(t)x+θσLl)Jx ≥0, 对花括号中式子关于ω(t)和B(t)求导, 得 解出式(4.9), 式(4.10), 我们有 将它们代入式(4.8)得到: 方程两边同时乘以eρt: 然后求解偏微分方程(4.12).猜测解的形式为 在函数J(t,x,l)=e−ρtQ(x,l)两边分别对t,x, 和l求导, 得 将它们代入式(4.12), 得下面的式子 假设Q(x,l)=A(x2+2kxl+gl2+ux+hl+f),则Qx=2Ax+2Akl+Au,Ql=2Agl+2Akx+Ah.代入(4.14)得到: 将式(4.15)分解为: 解式(4.16), 得到 因为 则 因此, 可以分别确定最优投资策略和最优支付率为: 2) 若σLlJl+ (σω(t)x+θσLl)Jx <0, 然后应用上述过程中类似的方法, 也可得到结果(4.20), (4.21), 其中, 注最优投资策略ω∗(t), 最优支付率B∗(t)和最优值J(t,x,l)与参数xp,bm,α,α1,α2,ρ,r,θ,µ,σ,µL,σL和养老金基金水平x, 工资水平l相关. 定理4.1对于优化模型(4.7), 给出最优投资策略: 和最优支付率: 本文在不确定理论框架下, 运用不确定最优控制理论, 将背景因素纳入不确定系统的最优控制模型中, 提出了一种新的不确定系统最优控制模型.利用不确定动态规划法, 得到了带背景状态变量的不确定最优性原理和不确定最优性方程.作为应用, 求解了具有不确定工资的养老金最优投资策略问题, 通过求解不确定最优性方程得到养老金最优投资策略和最优支付率的显示解.通过对比分析, 我们发现在乐观值准则下, 养老金成员的工资水平越高, 其投资于风险资产的比例就越高.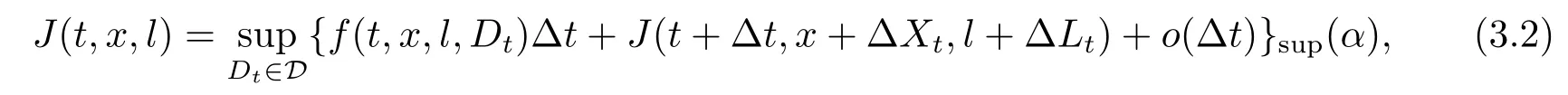

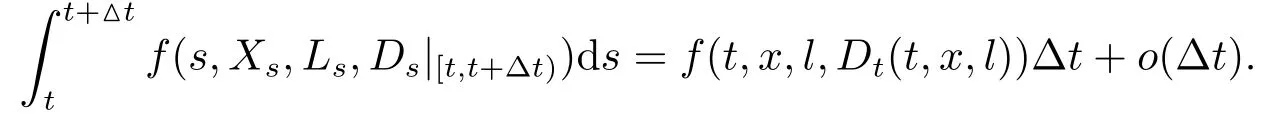
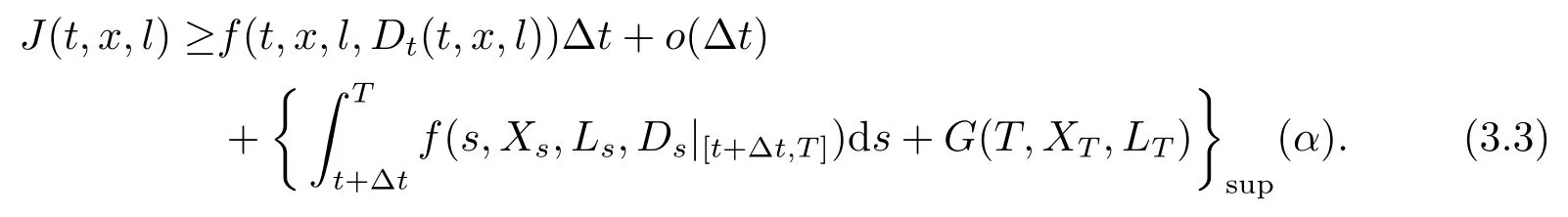
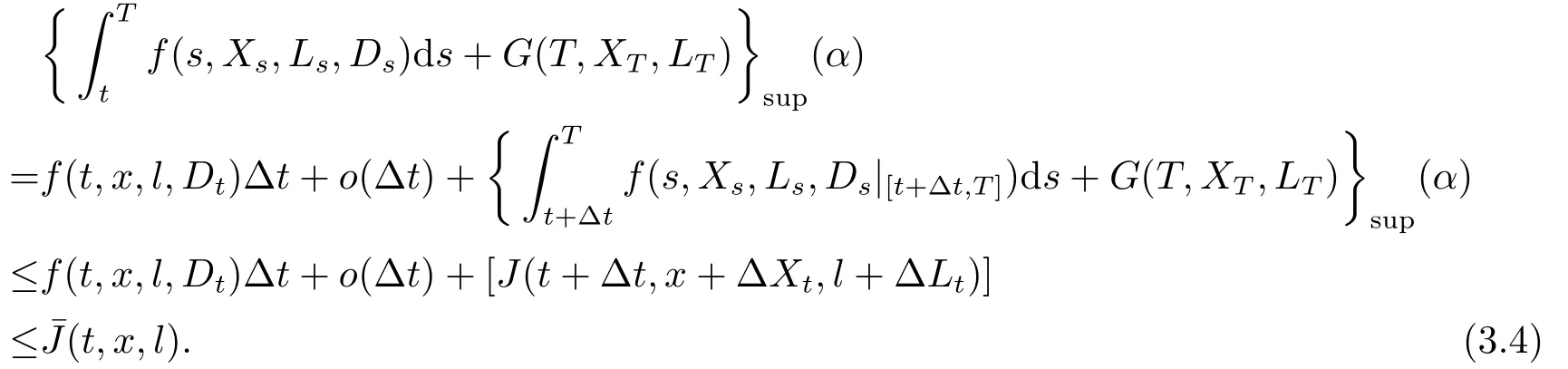


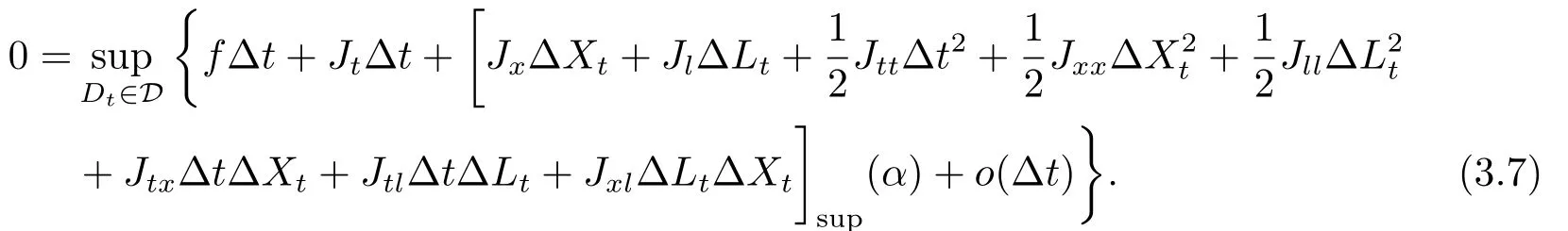
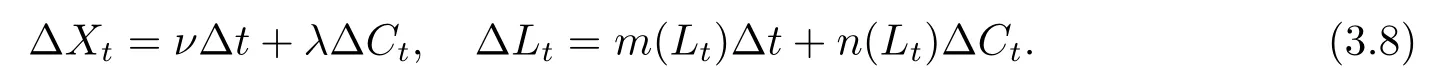
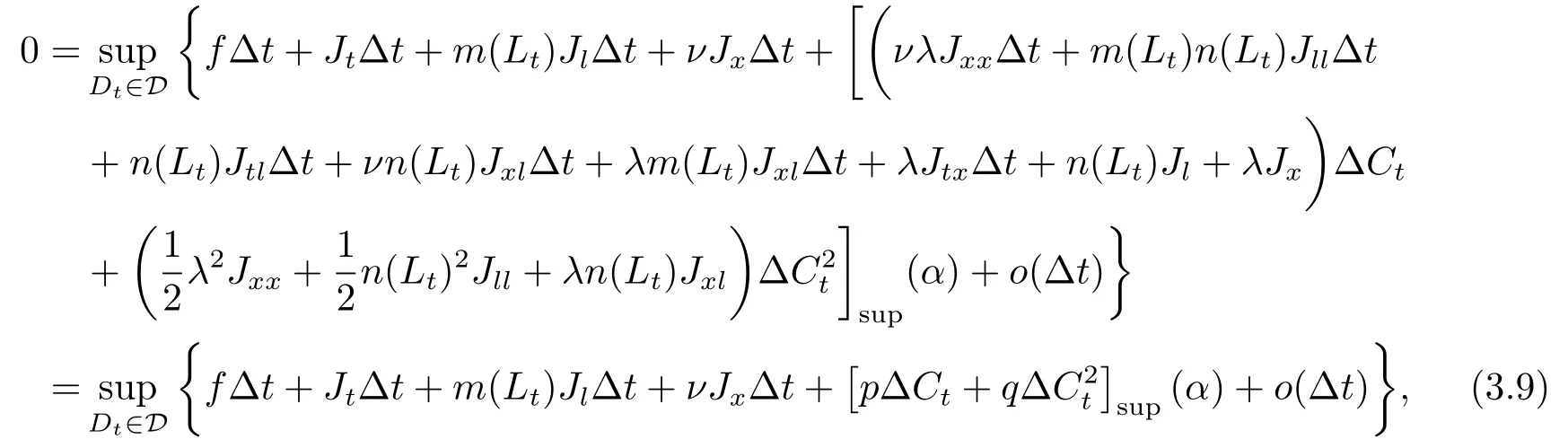
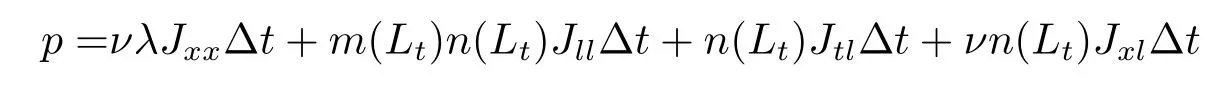
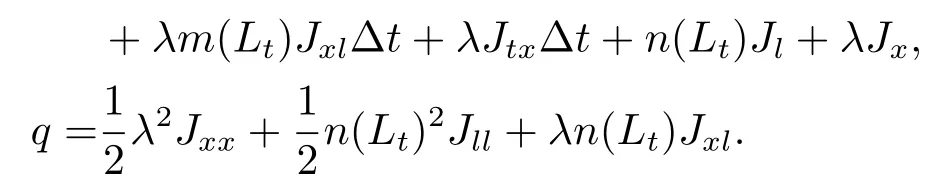
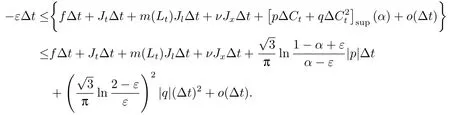
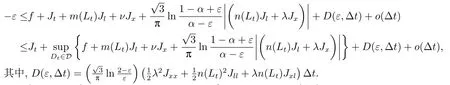
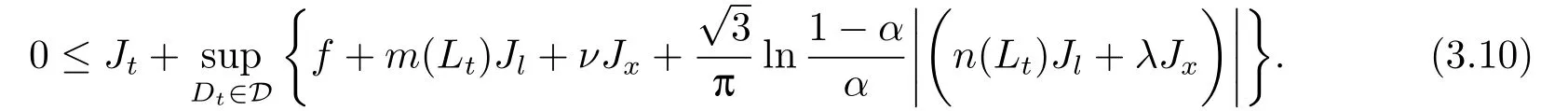
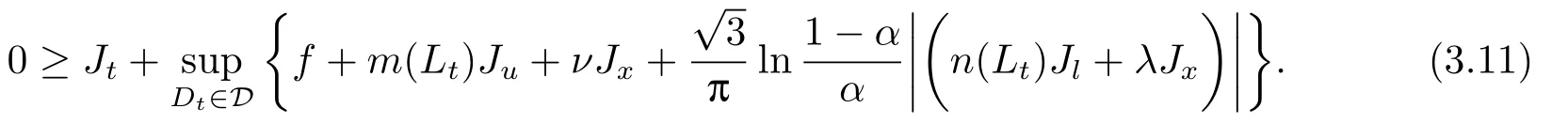
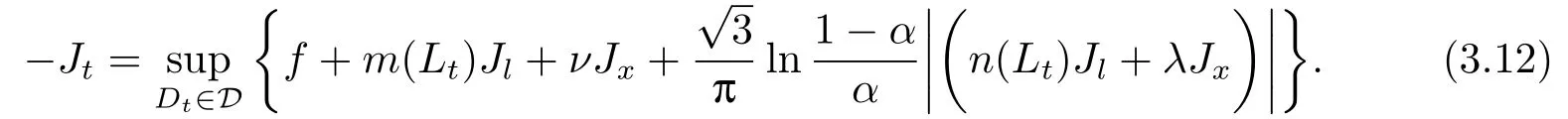
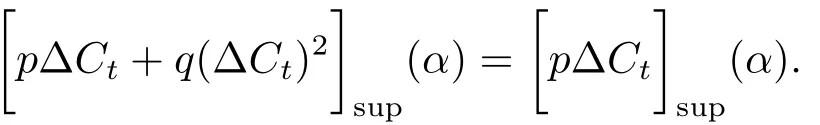
4.DC 型养老金的控制问题




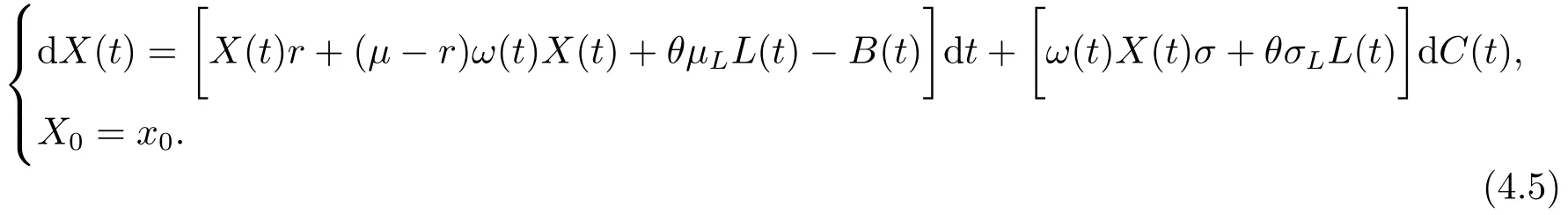

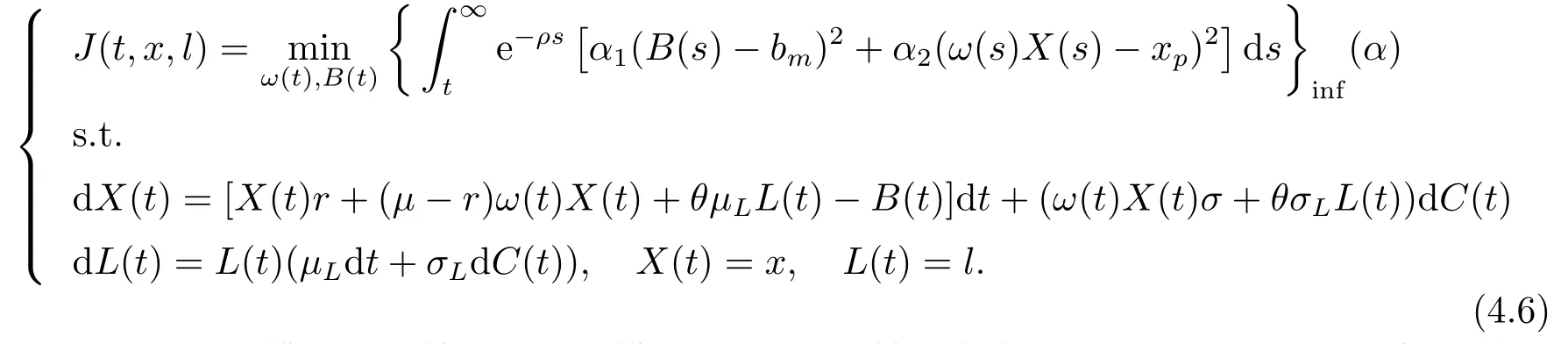



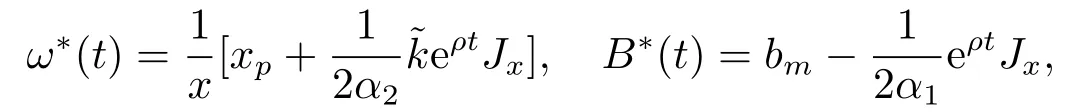
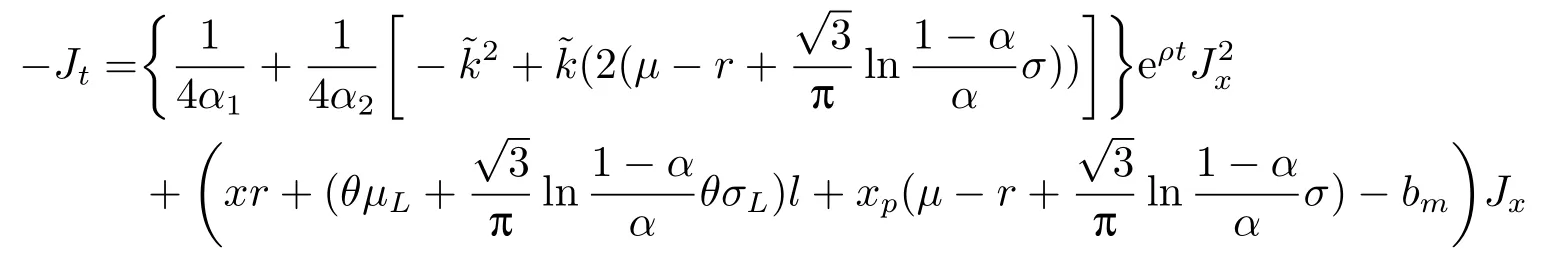

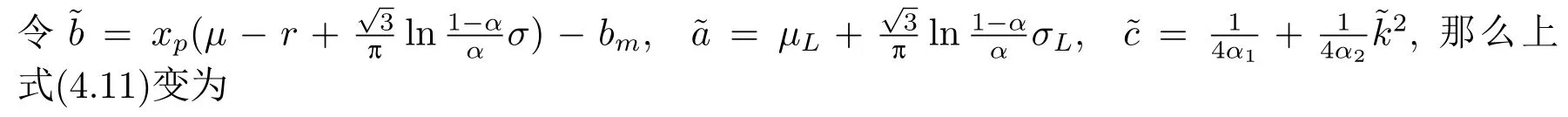




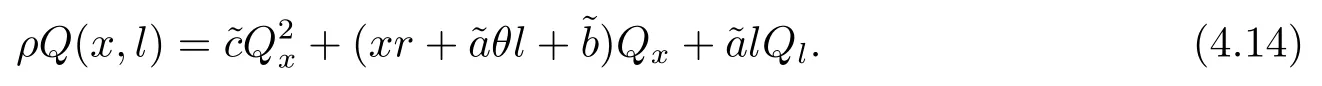
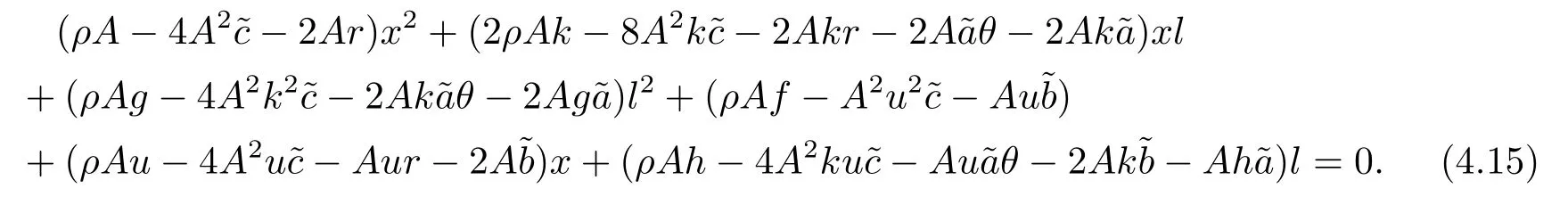


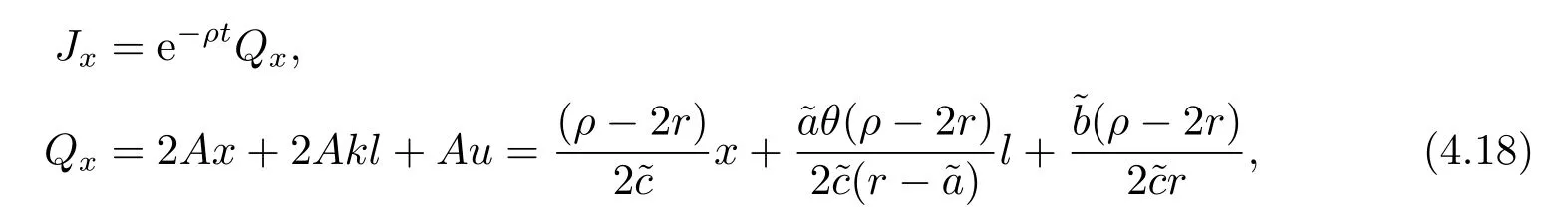
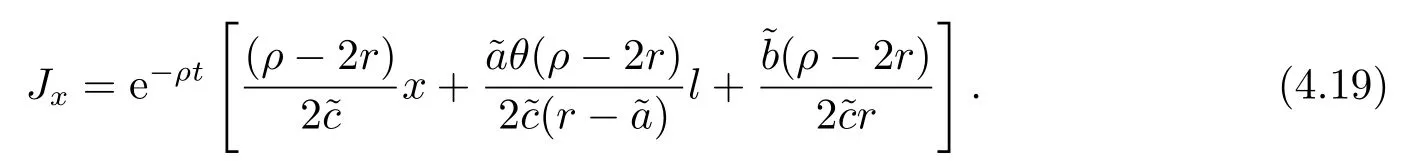
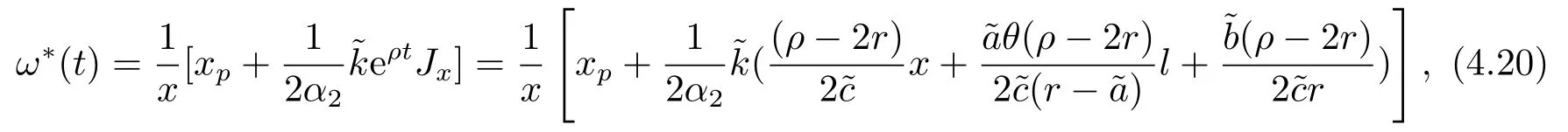
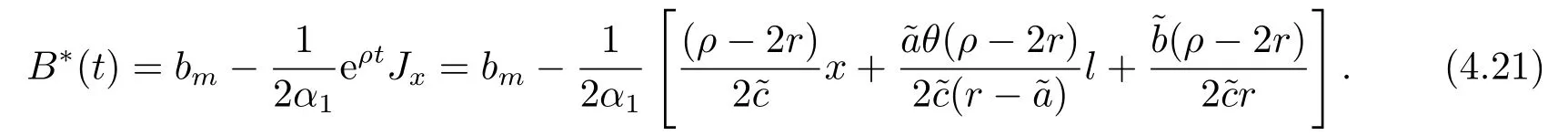
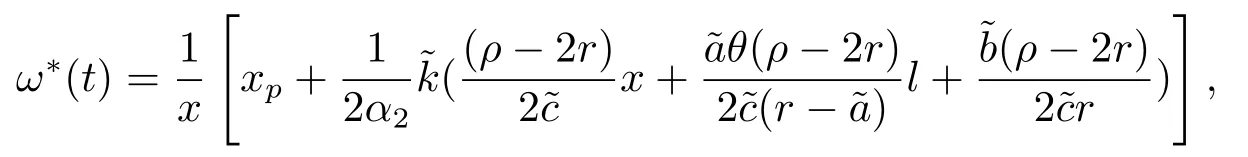
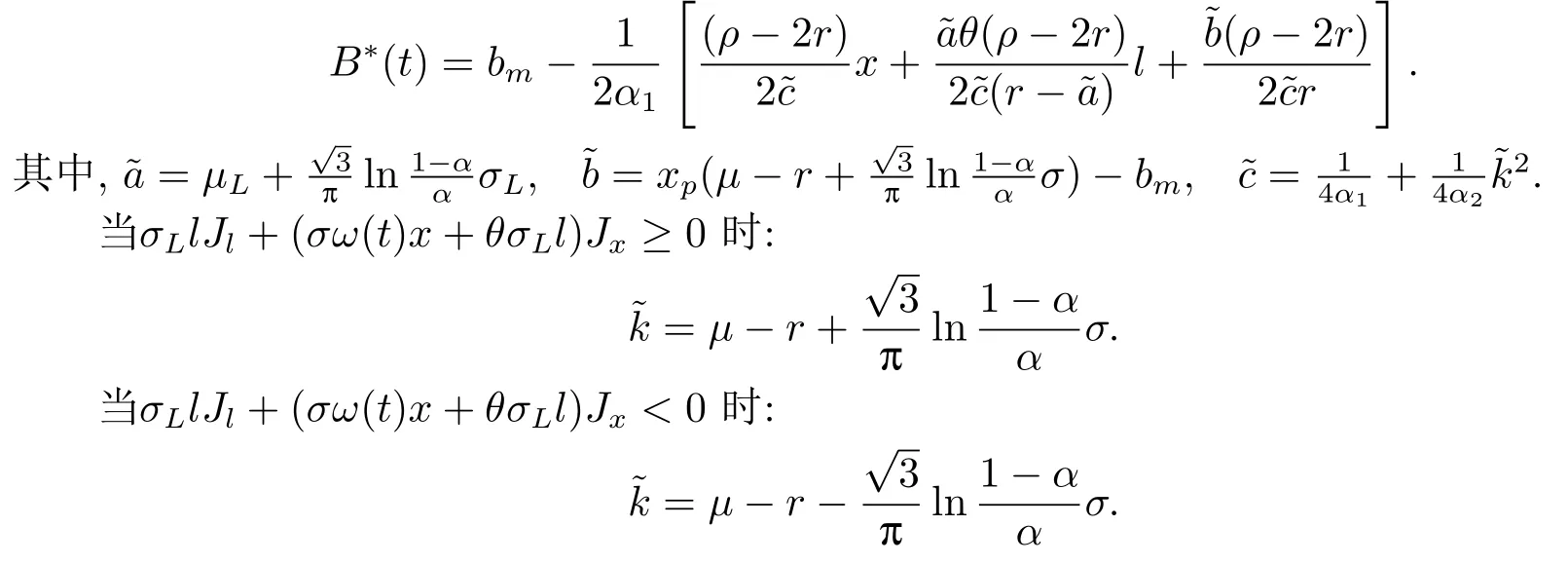
5.结论
猜你喜欢
杂志排行
应用数学的其它文章
- Dependence of Eigenvalues of Two-Interval Third-Order Boundary Value Problems
- 一类拟线性薛定谔方程非平凡解的存在性
- The Optimal Error Estimates for the Dynamic Magnetic Field of Solar Interface Problem by H(curl,Ω) Finite Element Methods
- 协变量维数可以趋于无穷的纵向数据的广义估计方程分析
- 不可压磁流体力学方程组的高精度数值解法
- Error Analysis of Kernel Regularized Regression with Deterministic Spherical Scattered Data
