结构不良试题命题趋势研究

山东 尹承利

结构不良试题是始于2020年新高考Ⅰ卷(供山东使用)的一种新题型.该题型的引入，增强了试题的开放性，引导考生的思维从知识的习得与记忆更多地转向问题的解决策略的选择上，使得数学真正地应用在思维层面，能深入地考查考生的观察、分析、比较、判断和对问题的把控能力，有效地考查考生思维的灵活性和建构数学问题的能力，以及分析问题和解决问题的能力.对数学理解能力，数学探究能力的考查起到积极、深刻地作用.因而该题型一经出现，就受到中学数学界的“热捧”，成为高考及各地模拟考试数学命题的“主打”题型.随着高考命题改革的推进，结构不良试题呈现出多元化趋势，无论是从形式还是考查内容上，都在变化发展着.从结构形式上看，2020年高考主要是“条件开放”型，而2021年高考甲卷理科的第18题呈现的则是“条件和结论均开放”型；从考查内容上看，2020年高考和各地模拟题中所考查的知识大多局限于数列和解三角形两部分内容，而2021年高考新高考Ⅱ卷的第22题(压轴题)将考查知识扩展到导数；从题型上看，2020年和2021年高考仅局限在解答题中，但可以预见，在2022年乃至以后高考命题中，结构不良试题的命题不止是解答题，也会在选择、填空题中呈现.为此，笔者原创、改编一组以解析几何为知识载体的结构不良试题，供2022届高三复习备考时参考，同时期待与诸位同仁共同致力于研究、预测结构不良试题在题型方面的变化发展趋势.

一、“结构不良”客观题

在选择题或填空题中设计“结构不良”试题，在现行的数学命题中未曾有过，但笔者以为，由于当今高考数学命题的多样性、开放性和包容性，在高考命题中出现“结构不良”选择题或填空题是可以预期的，呈现的形式与“结构不良”解答题呈现的形式基本一致.在这里，笔者编拟几题，旨在抛砖引玉.

1.“结构不良”选择题

题1.已知O是坐标原点，A,B两点分别在两条互相垂直的直线2x-y=0和x+ay=0上，且________，则线段AB的长为

( )

A.11 B.10

C.9 D.8

注：从以上两个条件中任选一个，补充在上面问题中并作答.

解析：若选择①，

由已知两直线互相垂直可得2×1+(-1)×a=0，解得a=2，所以△AOB外接圆的周长为10π，所以半径r=5.

又在Rt△AOB中，O是直角顶点，所以AB为△AOB外接圆的直径，所以|AB|=10，故选B.

若选择②，已知两直线互相垂直可得2×1+(-1)×a=0，解得a=2.所以线段AB的中点为P(0,5)，且AB为Rt△AOB的斜边.因为直角三角形斜边上的中线PO的长为斜边AB的一半，且|PO|=5，故|AB|=2|PO|=10,故选B.

( )

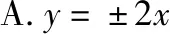
注：从以上两个条件中任选一个，补充在上面问题中并作答.

解析：若选择①，

若选择②，

2.“结构不良”填空题

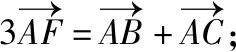
注：从以上两个条件中任选一个，补充在上面问题中并作答.

解析：若选择条件①，

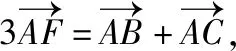
所以x1+x2+x3=3,y1+y2+y3=0.

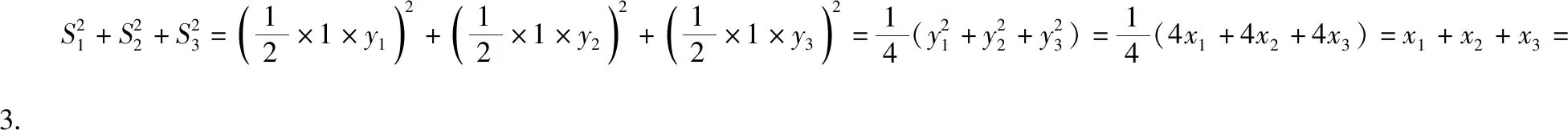
若选择条件②，

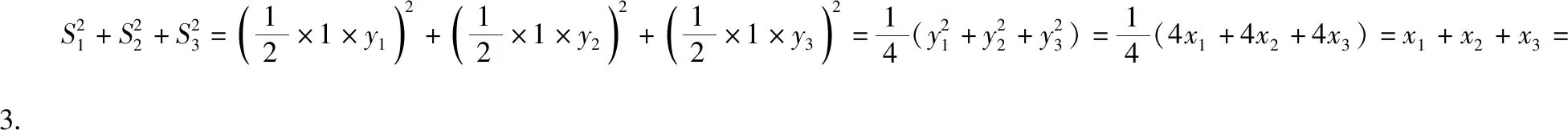
二、“结构不良”主观题

这是结构不良试题的主要呈现题型，条件开放(自选)，具体的表现形式是：给出几个待选条件，需要考生在较短的时间内，分析和捕捉信息，从所给出的不同条件中由考生自行筛选出自己认为擅长、适合的那一个条件，将其纳入、补充到题设条件中，并结合题设中的其它已知条件，然后按结构良好型试题作答的方法步骤进行推理、运算，以求取得满意的解答.

解题需要考生注意的是题目结尾标注的指导语——“如果选择多个条件分别解答，按第一个解答计分”，以免误答、多答，浪费时间.

(1)求椭圆E的方程；

(2)已知直线l与椭圆E交于A(x1,y1),B(x2,y2)两点，O为坐标原点，M为AB的中点，________.若存在实数t，使得|OM|·|AB|≤t恒成立，求t的最小值.

从下面两个条件中任选一个，补充在上面的问题中并作答.

注：如果选择多个条件分别解答，按第一个解答计分.

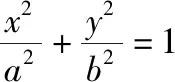
(2)若选①，

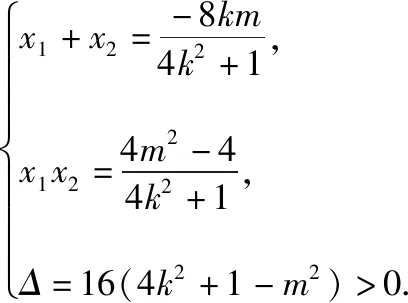
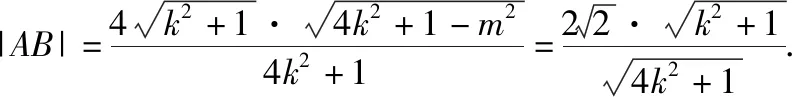
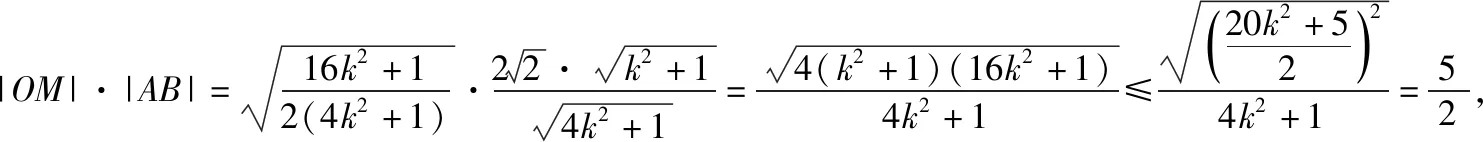
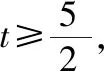
若选②，

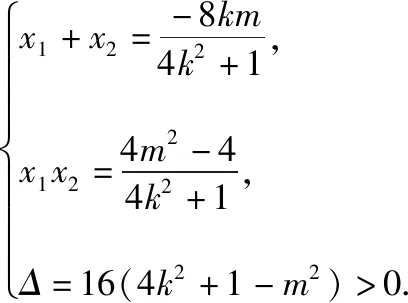
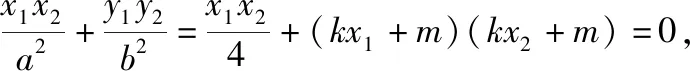
所以(4k2+1)x1x2+4km(x1+x2)+4m2=0，

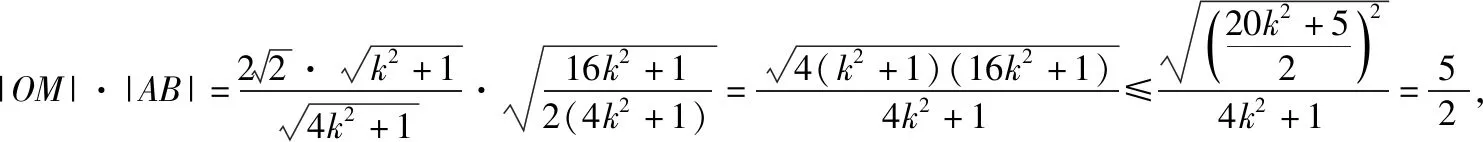
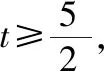
题5.已知动点M到定点F(1,0)的距离比M到定直线x=-2的距离小1.

(1)求点M的轨迹C的方程；

(2)已知________，求证：直线AB恒过一个定点.

从下面两个条件中任选一个，补充在上面的问题中并作答.

①O是坐标原点，P(-3,0)，A,B是C上的两个动点，且OP平分∠APB;

②过点F作C的两条互相垂直的弦，且弦的中点分别为A,B.

注：如果选择多个条件分别解答，按第一个解答计分.

解析：(1)由题意,动点M到定点F(1,0)的距离等于M到定直线x=-1的距离，根据抛物线的定义可知，点M的轨迹C是抛物线.

因为p=2，所以抛物线方程为y2=4x.

(2)若选择①,设A(x1,y1)，B(x2,y2)，设直线AB的方程为x=ky+m，代入抛物线方程并整理得y2-4ky-4m=0，由Δ=(4k2)-4(-4m)>0，解得m+k2>0，

所以y1+y2=4k，y1y2=-4m.

因为PO平分∠APB，所以∠OPA=∠OPB，所以kPA=-kPB，即kPA+kPB=0.

而y1(x2+3)+y2(x1+3)=y1(ky2+m+3)+y2(ky1+m+3)=2ky1y2+(y1+y2)(m+3)=2k×(-4m)+4k(m+3)=12k-4km，

所以12k-4km=0，由于k可以变动，所以m=3，即x=ky+3，当y=0时，x=3.

所以直线AB恒过定点(3,0).

若选择②,

设过点F作C的两条互相垂直的弦分别与C相交于为P,Q和M,N，且弦PQ的中点为A，弦MN的中点为B.

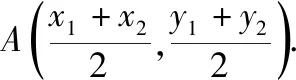
由题意可设直线PQ的方程为y=k(x-1)(k≠0)，

Δ=(2k2+4)2-4k4=16k2+16>0,

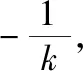
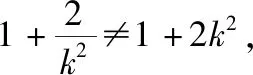
于是，直线AB恒过定点(3,0)；

当k=±1时，直线AB的方程为x=3，也过点(3,0).

综上所述，直线AB恒过定点(3,0).

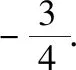
(1)求点P的轨迹C的方程；

(2)设直线l经过点M(0,1)，且与C相交于E，F两点，若________，求直线l的方程.

从下面两个条件中任选一个，补充在上面的问题中并作答.

注：如果选择多个条件分别解答，按第一个解答计分.

(2)若选择①，

当过点M的直线EF的斜率存在时，设直线EF的方程为y=kx+1.

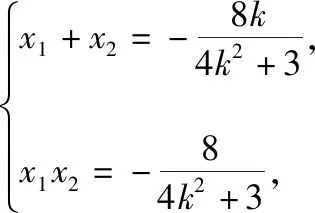
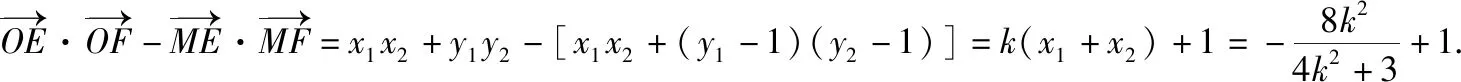
若选择②,

得(3+4k2)x2+8kx-8=0.①

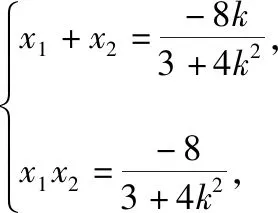
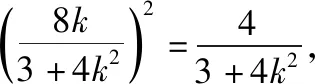
三、教学启示

结构不良试题作为一种新颖题型的确给新高考试卷命题注入了新的活力，复习备考中在关注、重视和研究这种新题型的同时，也切莫风声鹤唳.“结构不良”仅仅是一种载体，一种为高考命题服务的形式，它的“新”主要还是体现在情境、设问等形式上的新，在复习备考中重视研究、探讨和运用这些新题型的时候，更要重视在“新”的背后，考查的依然是核心的数学知识，考查的是数学本质性的东西，复习备考中做好以下几方面工作应当是坚定地！

1.夯实基础，注重通性通法

中学数学传统意义上的主干知识如函数与导数、三角函数、解三角形、数列、立体几何、解析几何、概率与统计等是构筑“中学数学”这座大厦的根基，无论高考改革到什么程度，相信对这些主干知识的考查一定不会冷落.因此要指导学生“吃透课本、抓实基础、注意通性通法，理解中心思想”，才能在高考中考出理想成绩.

2.把握“问题本质”

相信高考数学命题无论怎么变化、改革，改变的是形式，不变的是本质！数学问题的本质就是体现和渗透在问题中的知识、方法和规律及数学思想方法乃至数学核心素养，将本质性的东西深刻挖掘了、弄熟吃透了，即使当呈现在大家面前的新问题可能是在原问题的基础上进行了某种程度的改头换面，或者进行了适当的变式或包装，只要能看透变式与包装背后本质性的东西，那么问题无论如何变幻莫测，解决起来总能游刃有余和得心应手.

3.不盲目追求题量