运用样例探究 升华学生核心素养——以“解三角形”一章复习为例

广东 王铁成

高三数学复习大多为“做题——讲题”模式，老师力求把题型覆盖全面，学生的负担自然重，机械的训练不利于提高学生的核心素养.这就需要一些典型的样例为载体.样例是指教师提供以逐步呈现解题步骤的形式来为学生提供问题解决方法的例题.样例分不完整样例和完整样例，不完整样例在呈现方式、设问方式，以及答案组织方面具有某种不完整性，教学情境更具生成性、开放性和不确定性，能更好地激发学生的积极性和创造性，从而提高学习效果，从某种意义上讲契合高考新题型——结构不良试题.有助于帮助学生搭建知识网络，培养学生提出问题、解决问题的意识和能力，升华核心素养.但是这种样例的学习方式对学生的基础知识要求较高，同时要求学生有一定的自学能力和理解能力.高三毕业班的学生恰好大多都具备这个条件.本文以“解三角形”为例，尝试运用“样例”探究新模式，打破“做题——讲题”死循环，提高课堂效率，落实《普通高中数学课程标准(2017年版2020年修订)》(以下简称《课程标准》)理念，升华核心素养.

1.探究不完整样例 复习本章主干知识点

“解三角形”一章中最重要的几个基本知识点：正弦定理、余弦定理、射影定理及它们的证明和应用，下面我们通过案例研究任意三角形中的“向量的等量关系”，通过不同的数学方法处理，证明定理.

2.创设条件与结论互换的样例 加深对基本定理的认识

在高中数学教学中，我们会发现很多数学命题中的原命题和逆命题都是真命题，因此我们可以通过将问题与条件互换，创设样例，教师给出命题充分性的证明，由学生来补充命题的必要性条件，反之亦然.在这个活动中学生能够充分体会到知识运用和问题思考的双向性，有利于培养学生的发散性思维，认识到事物的对立与统一.

案例2正弦定理、余弦定理的相互推导证明

视角一：用正弦定理推导余弦定理(以a2=b2+c2-2bccosA为例)

b2+c2-2bccosA

=4R2(sin2B+sin2C-2sinBsinCcosA)

=4R2[sin2B+sin2C+2sinBsinCcos(B+C)]

=4R2[sin2B(1-sin2C)+sin2C(1-sin2B)+2sinBsinCcosBcosC]

=4R2(sinBcosC+sinCcosB)2=a2.

视角二：用余弦定理推导正弦定理

sin2C=1-cos2C

通过“公式互推”样例的活动组织，让学生在公式“对象”和“过程”的双重身份中不断切换思维对象，不断感知数学推理的力量，同时加深对两个基本定理的认识.这样的活动组织可以提高学生的推理论证能力，拓宽认识公式的视野，贯通知识间的联系.

3.创设确定条件变换结论样例 建立数学模型

在高中数学学习中，还有一类问题就是题目的条件非常类似，甚至相同.由于考查的目标不同，可以采用不同的提问角度创设结论.如果学生能够在这种通过结论变换创设的“不完整样例”的活动氛围中学习，必定能够增强思维的深度，提高运用所学知识的能力.

案例3△ABC中，角A，B，C所对的边分别是a，b，c，若a=6，∠A=60°，请添加结论，形成一个完整习题.

学生根据已有的基本知识设计习题，部分具有代表性的习题，选取如下：

问题1：求b+c的取值范围；

问题2：求三角形周长的取值范围；

问题3：求bc的取值范围；

问题4：求三角形面积的最大值.

本案例实际上呈现了解三角形中的一个最重要的模型“给出定边及其所对的角”，其他结论部分可以设计求一些基本量的最值问题，其实这也是很好的一道结构不良试题.学生如果能从单纯的解决问题上升到能够编撰习题的高度，那么课堂是非常成功的.既能促进学生的深度学习，训练学生的基本技能，同时发展学生的数学认知，提高数学素养.

4.创设能够多视角解题的样例 铺设学生知识网络

教育家波利亚说过“即使是相当好的学生，当他得到问题的解答后，就会合上书本，找点别的事来干，这样做，他就错过了解题的一个重要方面”.如果教师能使学生在每次解题之后扪心自问:“这道题的解法是否完善?这道题有没有更好的解题途径?能不能换个角度考虑一下?还能不能再推广呢?”，在不同角度的解法间切换，那么学生就会融会贯通各个知识点，形成知识团，学生的核心素养品质必然由量变产生彻底的质变.

案例4解决案例3的问题4

视角一:借助余弦定理和均值不等式

因为a，∠A已知，△ABC面积的最大值可转化为求bc的最大值，所以用余弦定理建立b，c之间的关系，在此基础上用基本不等式求最值.

视角二:借助正弦定理和三角函数的性质

视角三:借助平面几何知识

案例5(2021·新高考Ⅰ卷·19)记△ABC的内角A，B，C的对边分别为a，b，c.已知b2=ac，点D在边AC上，BDsin∠ABC=asinC.

(1)证明：BD=b；

(2)若AD=2DC，求cos∠ABC.

解：第(1)问较为简单，请读者自行解决，由于篇幅不再赘述，我们集中精力解决第(2)问.

视角一：借助余弦定理

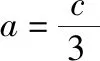
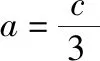
另解：也可以在△ABD中和在△ABC中使用余弦定理，即利用∠BAD=∠BAC也可以求解.

视角二：借助平面向量

再由余弦定理b2=a2+c2-2accos∠ABC，及b2=ac得到6a2-11ac+3c2=0下同案例5视角一.

视角三：借助平面几何知识(勾股差定理和托勒密定理)

知识面更宽的学生，或者参加过竞赛培训的学生，其实还有更容易的平面几何方法，比如勾股差定理和托勒密定理.

5.创设“错中悟道”样例 深化学习品质

高三讲评课涉及的内容都是学生已学过的知识，学生会觉得课堂很平淡，但是解三角形里面的运算有时形式化技巧用得较多，如果在学生算出了结果后，我们引导学生去质疑，你的结果正确吗？那么课堂效率就会显著提高.同时也会培养学生的质疑批判精神，错中悟道.

①∠A的大小；

②若a=6，b+c=8求△ABC的面积.

这样的错中悟道样例探究，也正是《课程标准》所要求的“在学生进行活动的同时，给学生树立敢于质疑、善于思考、严谨求实的科学精神，不断提高实践能力，提升创新意识.”

6.结束语

上述的几个案例层层递进，从知识的3个层次，了解、理解、运用来提高，特别是在高三复习的阶段，学生会以这些案例为载体，把解三角形的相关知识融会贯通成知识团，再有机添加到自己所拥有的高中数学知识网中，并且不断地壮大和凝练！6个案例基本表征如下：