解析几何教学中提升数学运算素养的研究——以2021年新高考Ⅰ卷第21题为例

福建 陈崇荣

数学运算素养是数学学科六大核心素养之一，数学运算主要包括理解运算对象，掌握运算法则，探究运算思路，选择运算方法，设计运算程序，求得运算结果等.解析几何是提升运算素养的主要载体，本文就2021年新高考Ⅰ卷第21题谈谈数学运算素养的培养.

(1)求C的方程；

1.探寻学生解题的心路历程及“卡壳”原因

试题的呈现方式简洁、易懂，解题思路也比较明确，但得分率不够理想，学生普遍反映计算量大，计算过程不顺利.笔者仔细研究试题后，针对第(2)问与几位同学进行了交流.

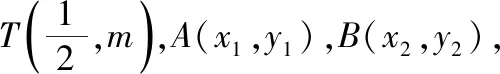
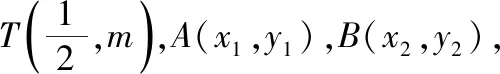
2.直线方程的点斜式VS斜截式

从上面可以看出，设直线方程时学生1和学生2都选择直线的点斜式方程，学生3选择的是斜截式方程，笔者顺着学生的思路进行解答，过程如下：

设直线的点斜式方程解法：

设直线的斜截式方程解法：

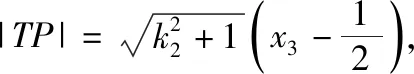
点评：解析几何本质是以代数的角度研究几何问题，代数运算是避不开的，如何进行有效的运算，优化运算，提升学生的数学运算核心素养值得研究.直线点斜式方程和斜截式方程各有优点，也是平时教学中常提倡的设法，表面上看已知直线的斜率及过一点一般设点斜式，已知直线的斜率及截距一般设斜截式，但从上面三位学生的解题分析看,此题用斜截式优于点斜式，因此在解题教学中引导学生在选择直线方程时，要斟酌，会涉及后面的运算量的大小.例如要把直线方程(含两个参数)代入二次曲线方程消元时，涉及平方，直线方程可以考虑设斜截式，因为斜截式中项比较少.

3.探寻优化运算之路

3.1平移直角坐标优化数学运算

坐标轴平移法：

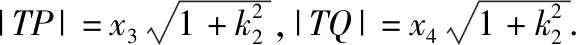
3.2探寻试题来源 提炼解题经验 优化数学运算

本题背景是四点共圆问题，四点共圆主要有两个定理:

定理1：AB和CD是圆锥曲线的两条相交弦，且AB与CD交于点P，则四点A，B，C，D共圆的充要条件是直线AB与直线CD的倾斜角互补.

定理2：AB和CD是圆锥曲线的两条相交弦，且AB与CD交于点P，则四点A，B，C，D共圆的充要条件是|PA|·|PB|=|PC|·|PD|.

关于四点共圆的问题在高考、竞赛中多次出现，解决四点共圆问题主要有四种方法，一是利用直线参数方程的几何意义，二是利用曲线系方程，三是利用两直线的夹角公式，四是利用平面几何知识.下面就利用直线的参数方程和曲线系方程来解2021年新高考Ⅰ卷第21题，体会以往解题经验优化数学运算的优势.

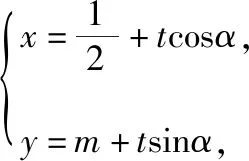
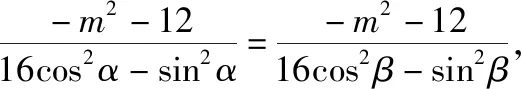
点评:《普通高中数学课程标准(2017年版2020年修订)》中直线的参数方程不作要求，但笔者认为教师有必要高屋建瓴的把握试题的解法、立意等，恰当运用曲线的参数方程，优化有关解析几何的数学运算.

点评:二次曲线的方程一般为Ax2+By2+Cxy+Dx+Ey+F=0，高中阶段涉及圆、椭圆、双曲线、抛物线.

若直线l1:A1x+B1y+C1=0，l2:A2x+B2y+C2=0，则(A1x+B1y+C1)(A2x+B2y+C2)=0可以认为是非退化的二次曲线.

若曲线C1:f1(x，y)=0，曲线C2:f2(x，y)=0，则过两曲线交点的曲线系方程可表示为λf1(x，y)+μf2(x，y)=0(λ∈R，μ∈R)，当确定所求曲线不是C1或C2时，可以设一个参数，即为f1(x，y)+λf2(x，y)=0.

4.提升数学运算核心素养的教学反思