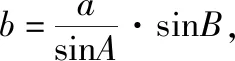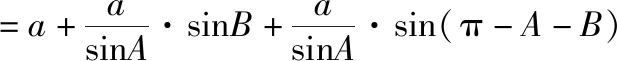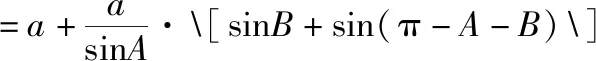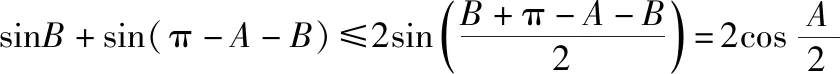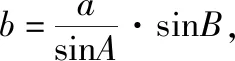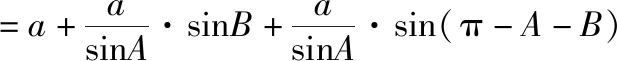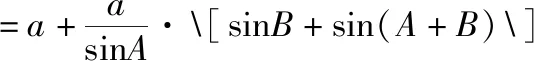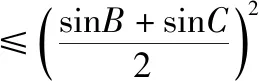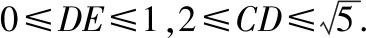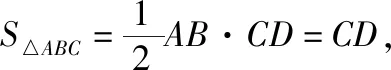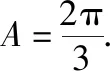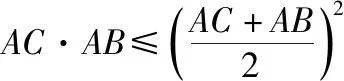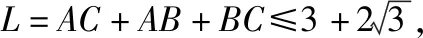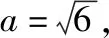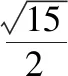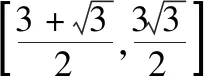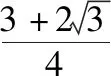探讨求解三角形周长与面积的范围

四川 唐有强

在数学一轮复习备考教学过程中,如何实现高频考点的突破，解决教学难点，从做一个试题，到会一类试题，达到触类旁通；如何做到挖掘典型试题，从一题多变、一题多解、一题优解到万题归一，从而启迪学生的思维，品味数学试题的精髓.本文笔者将以求解三角形中的周长、面积的取值范围问题为例，呈现教学片段，以供参考.

纵观求解有关三角形的周长或面积的取值范围问题，在高考真题与模拟试题中的基本模式为已知三角形的一边及其对角，求解三角形的周长或面积的最值或取值范围问题.为让学生主动掌握此类问题的求解技巧和解题环节，笔者设计了如下几个教学环节：

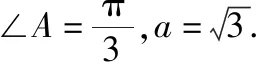
(1)△ABC的周长取值范围是;

(2)△ABC的面积的最大值为.

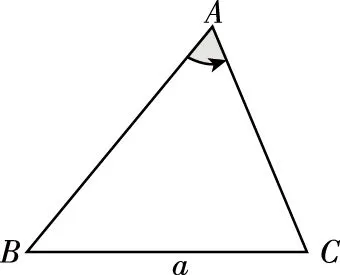
环节一：试题分析与求解：在分析中找准试题的突破点与解题策略

提问：品味试题，弄清试题已知什么，求解什么，如何寻求突破点？

学生1：由求解范围、最值，我想到的突破点为借助三角函数工具.

学生2：不等式也可以求范围，我想能否从不等式角度找到突破口.

老师：两位同学的思维都有一定的代表性,那又如何建立函数或不等关系呢?请同学们继续思考.

学生3：既然是三角形，我想到正弦定理，以角为自变量建立函数关系，思路如下:

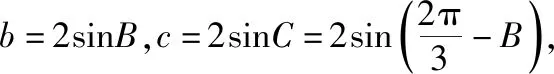
将周长与面积都建立成关于角B的三角函数关系式，再求解.

老师：很好，学生3的思路很清晰，但要提醒同学们注意两点：①角B是否有取值范围，②三角恒等变换力求准确.除了这个思路，不等式能求解吗？

老师：学生4的思路很清晰，设想构建合理，我想问一下同学们，整个过程中是否有缺陷？

学生5：好像最后只能得到目标的最大值或最小值，但范围是否还缺点什么？在求三角形的周长时，是否还要用到隐含条件：任意两边之和大于第三边，任意两边之差小于第三边.

老师：学生5的思维非常严谨，考虑非常仔细，结合上面5位同学的思路，请同学们马上整理思路，书写试题解析 ：

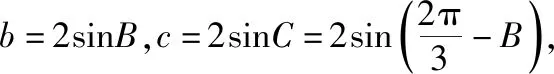
于是△ABC的周长为

△ABC的面积为

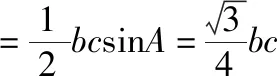
解法2：在△ABC中，由余弦定理得,

a2=b2+c2-2bccosA,

所以3=b2+c2-bc=(b+c)2-3bc.

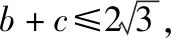
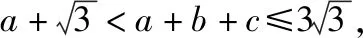
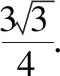
评析：通过以上两种方法的比较，解法1侧重三角恒等变换，对学生在三角化简方面有较高要求;解法2侧重代数结构分析和不等式的变形转化，对学生在代数结构分析方面有较高要求，从解答过程中发现，当涉及范围问题，建议用解法1，涉及单边最值问题，建议用解法2.

环节二：试题升华、归纳总结：在提炼中研究试题，在研究中优解试题

提问：同学们在试题整理和解答中，是否有其他的发现？

学生6：感觉周长和面积的最大值都在三角形为等腰三角形时取得.

学生7：已知三角形的一边及其对角，由正弦定理可得这样的三角形的外接圆的半径是一个定值.

老师：结合两位同学提出来的思考，我们一起来探索一下看看有什么新的发现.

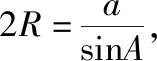
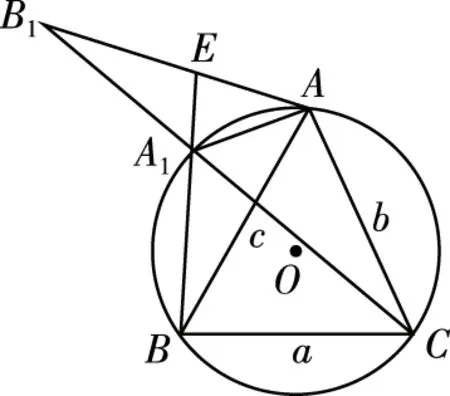
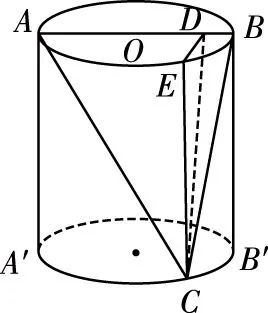
命题：已知△ABC是以A为顶角的等腰三角形，在圆周上任取(异于点A,B,C)一点A1，连接A1B,A1C，证明：A1B+A1C

延长CA1至点B1,使得A1B1=A1B，则A1B+A1C=CB1.连接AA1,AB1,延长BA1交AB1于点E,

因为A,A1,B,C四点共圆，所以∠EA1A=∠BCA,

因为AB=AC,所以∠AA1C=∠BCA,

则有∠EA1A=∠AA1C，而∠B1A1E=∠BA1C,

故有∠B1A1A=∠BA1A，而A1B1=A1B，AA1=AA1,

则△AA1B1≌△AA1B,

于是AB1=AB,

故AB+AC=AB1+AC

>B1C=A1B1+A1C=A1B+A1C,

另外,要使△ABC的面积达到最大，由于底边a一定，只需高最大即可，结合三角形的外接圆，即高过三角形外接圆圆心，面积达最大值，实质就是底边a的中垂线过圆心与圆的交点，取得对应的点A,故△ABC为等腰三角形时，周长与面积取得最大值.

试题总结：结合上述证明过程得到如下结论：在三角形中，已知三角形一个内角及其对边，当三角形是已知角为顶角的等腰三角形时，三角形的周长与面积取得最大值.

公式推导△ABC的周长：

证法1:在△ABC中，A+B+C=π，所以C=π-A-B，

于是△ABC周长为

因为f(x)=sinx在x∈(0，π)上为凸函数，由凸函数的性质可得，

证法2：在△ABC中，A+B+C=π，所以C=π-A-B,

于是△ABC周长为

设f(x)=sinB+sin(A+B)

=(1+cosA)sinB+sinAcosB,

f′(x)=cosB+cos(A+B)=cosB-cosC，

令f′(x)=0,当且仅当B=C时成立，此时f(x)取最大值，

△ABC的面积：

(当且仅当∠B=∠C时取等号)，

环节三：体验反馈、高考链接

反馈训练1：(2021·上海卷·9)在圆柱中，底面圆半径为1，高为2，上顶面圆的直径为AB，C是底面圆弧上的一个动点，绕着底面圆周转，则△ABC的面积的范围.

过点C作CD⊥AB,过C作CE⊥⊙O,由三垂线定理可知DE⊥AB,

评析：本题以圆柱为背景，求解三角形的面积取值范围问题，考查空间中点、线、面位置关系与动点到直线的距离，打破了常规的命题角度，考查学生的综合能力和创新能力.解法1，结合圆柱中的点、线、面关系，把三角形的面积问题最终转化为点到线的距离问题.解法2，将立体问题平面化，研究动点C形成的三角形的面积问题，采用极限思维，借助三角形面积最值产生的条件，最终动点问题静态求解.

反馈训练2：(2020·全国卷Ⅱ理·17)△ABC中，sin2A-sin2B-sin2C=sinBsinC.

(1)求A；

(2)若BC=3，求△ABC周长的最大值.

解:(1)由正弦定理可得,BC2-AC2-AB2=AC·AB,

(2)由余弦定理得BC2=AC2+AB2-2AC·ABcosA=AC2+AB2+AC·AB=9,

即(AC+AB)2-AC·AB=9.

评析：本题以三角形背景，考查边角互化、正余弦定理的应用以及三角形的周长最值,第(1)问侧重考查学生对三角恒等式结构分析以及借助正、余弦定理实现边角互化，第(2)问考查三角形的周长最大值转化到边的最大值，可以直接借助余弦定理和基本不等式求得周长的最大值，另外也可以把边利用正弦定理转化到对应角的三角函数上，再利用三角函数的相关知识求解.

环节四：课后补偿，巩固提高

2.在△ABC中，角A，B，C所对应的边分别为a，b，c，且2acosC=2b-c,若a=1,求b+c的取值范围．

参考答案：(1,2]

(1)△ABC的周长取值范围是.

(2)△ABC的面积的最大值为.