回归定义促深思 深度学习拓视野

四川 王昌林 罗萍双

深度学习是根据学生自身经验从而满足自身需求的学习方式.其主要过程包括发现问题、解决问题、总结归纳问题、问题推广应用四个环节.深度学习还是一种文化的传承，教师若是热爱数学，对钻研数学问题有浓厚兴趣，勇于探究和创新，其品质和精神必然能潜移默化地感染学生，从而引领学生开展深度学习.积极开展深度学习，对于教师来说，可以促进自身专业发展，提高施教水平；对于学生来说，可以完善知识结构，提升创造和创新问题以及研究问题的能力.

1.问题提出

问题提出可以是人为引导产生的，也可以是偶然产生的.许多教师通过在课外拓展题、高考压轴题、自主招生的另类题以及竞赛试题中去有意寻找问题，从而提出问题，这个过程是较为低效的且许多问题是不利于开展深度学习的.问题提出应该是一个自然的过程，例如在教材的定义、例题和习题中.这些“接地气”问题的提出对深度学习的开展才是高效且有益的.

1.1问题提出背景

一位高三学生，学习成绩在班级处于中上游水平.学生在结束全部新课内容后对所学知识进行归纳整理时发现，椭圆与双曲线定义中分别是到两定点距离之“和”与到两定点距离之“差”，从而产生猜想如果是“平面内到两定点的距离之积或商为定值”又会是怎样的图象呢？于是自己尝试对猜想进行探索，有一些眉目却不能解决，于是想到寻找老师帮忙验证与完善.

1.2提出问题

椭圆的定义是平面内到两定点的距离之和为定值，双曲线的定义是平面内到两定点的距离之差为定值，一个是距离之和一个是距离之差，既然有了加和减，那乘和除呢？这样的曲线存在吗？有的话它们的动点轨迹分别又是什么样子呢？

2.问题解决

问题解决是深度学习的重点，问题解决与否决定着深度学习能否顺利进行.问题解决的方式是多样的，可以是教师主导，也可以是学生自主.在解决问题的过程中可以采取合作讨论、查阅研读相关资料与书籍、借助现代教育技术等多种方式.需要注意以下几点：

(1)要给学生充分的思考探究时间，宝剑锋从磨砺出，学生才能有所收获；

(2)在解决问题时回顾旧知识与方法，起到复习巩固作用；

(3) 暴露出真实的思维过程，教师既能及时纠正学生的错误，又能传授解决问题的经验；

(4)方法的引导与选取要“接地气”，要与学生的思维水平相适应；

(5)问题偏难应加强鼓励，推动深度学习积极进行.

以下为整理后的探究曲线方程片断：

师：针对所提出的问题？对于曲线方程，你做了哪些探究工作呢？

生：我类比探究椭圆方程的步骤，把曲线看作是平面内一动点的轨迹，并作如下探究：

取线段AB的中点为坐标原点，AB所在直线为x轴，建立如图1所示平面直角坐标系.

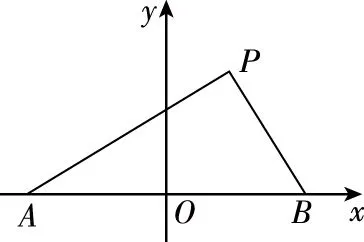
图1

设|AB|=2c(c>0)，即A(-c,0)，B(c,0).

设动点P的坐标为(x,y)，

等式两边平方化简可得(λ2-1)x2-2c(λ2+1)x+(λ2-1)y2=c2(1-λ2).

式子还不够简洁，但不知道后面该进行怎样的化简.

师：仔细观察，等式有没有什么共同的或者相似的地方？

学生认真观察后……

生：有，未知数x与y前都是λ2与1的加与减形式，减比较多，要不我们同时除以λ2-1？

师：想法没问题，但若是λ2-1=0，你还可以直接除以λ2-1吗？

生：那就分等于0和不等于0两种情况讨论.

学生开始分情况讨论，教师在旁指导，得到结果如下：

师：现在来看动点P的轨迹是什么？

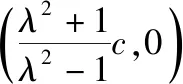
师：是的，我们把它称作阿波罗尼斯圆.顾名思义，阿波罗尼斯圆是古希腊数学家阿波罗尼斯在研究了众多的平面轨迹问题后得到的结果，即平面内到两定点距离之比为定值且动点的轨迹为直线或圆.

生：这个初中的时候有提到过,还可以叫阿氏圆,原来是它.

师：是的，类比我们刚才的方法，你能继续探究“积”所对应的曲线方程吗？

生：取两定点A，B，动点P满足|PA|·|PB|=λ(λ>0且为常数).取线段AB的中点为坐标原点，AB所在直线为x轴，建立如图1所示平面直角坐标系.

设|AB|=2c(c>0)，即A(-c,0)，B(c,0).

设动点P的坐标为(x,y)，

等式两边同时平方得(x2+2cx+c2+y2)(x2-2cx+c2+y2)=λ2，若是展开，等式左边项数过多，我觉得不正确，后面就没有继续探究了.

师：按照刚才的思考方式，再试试，看能不能继续探究呢？

学生仔细观察等式结构并思考后回答：

生：等式左边两因式中就2cx那一项的系数不同，其余部分都是相同的，我们将2cx调整位置后可以得到(x2+c2+y2+2cx)(x2+c2+y2-2cx)=λ2，将“x2+c2+y2”看成是一个整体，就可以得到(x2+c2+y2)2-4c2x2=λ2.

师：是的，还可以再化简吗？

生：等式看起来有些复杂，但是每一项都有平方，它是一个偶函数，轨迹应该是对称的.

师：我们用几何画板来看一下吧.(以下为几何画板作图的详细过程与结果)

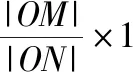
(1)连接PA，PB，并度量长PA与PB长度，点击[数据]-[计算]PA·PB的值，并[制表]PA,PB以及PA·PB的输出值.移动点N，得如图2所示的双纽线，PA·PB的值固定不变且与OM相等.

(2)左右移动点M，得以下轨迹：

师：我们发现点M其实是可以和点O重合，那我们前面有没有哪里需要改正的呢？

生：动点P应该满足|PA|·|PB|=λ(λ≥0且为定值).

师：是的，平面内到两定点的距离之积为定值的点的轨迹，我们把它称为卡西尼卵形线.和阿波罗尼斯一样，卡西尼也是一个人名，卡西尼卵形线是卡西尼在研究土星及其卫星的运行规律时发现的.关于轨迹方程，λ与c之间有这样的关系：

①当λ=0时，动点P的轨迹为两个定点A(-c,0)，B(c,0)；

②当0<λ

③当λ=c时，动点P的轨迹为图2所示8字形交叉的双纽线；

生：卡西尼卵形线竟然如此有意思，其中它变化多样的动点轨迹最有意思.卡西尼当时没有几何画板这些现代化的作图工具，能探究出来这些优美的轨迹和结论，真的太厉害了.

3.结论应用

深度学习是师生共同经历的一场智慧之旅.旅程的终点不是让学生获得一堆零散、呆板、无用的知识，而是让他们能够积极、充分、灵活地运用知识，去理解世界、解决问题，学以致用，获得人格的健全和精神的成长.理解不仅仅是单纯字面意思上的知道、了解、明白之意，它更强调一种深层次的思考，即解释、思辨、推理、验证、应用等更有难度、更加复杂和更具综合性的学习.

【解析】因为点M，N，T皆是在圆O上的点，

所以|OM|=|ON|=|OT|.

由切割线定理可知|OT|2=|OA|·|OB|，

所以|OT|2=|OM|2=|ON|2=|OA|·|OB|，

所以△OMA∽△OBM，△ONA∽△OBN，

【评注】在验证结论①正确性后就可以看出，应用1有着阿波罗尼斯圆的知识背景.

【应用2】给定平面上两个点F1(-1,0)，F2(1,0)，点P到这两点的距离的乘积为a2(a>1)，设点P的轨迹为曲线C.下列关于曲线C的说法中，正确的是.

【评注】应用2是以卡西尼卵形线为背景命制的试题，准确运用定点与定值的关系可以快速有效地判断结论①②的正确性.

【评注】应用3是教材习题，将定点改为定直线，探究曲线方程的方法和前面的探究是一样的，除此以外人教A版选修2-1的第47页、59页、65页等也有与应用3相类似的例题和习题.

4.教学思考

深度学习的发生是不经意间的，问题的提出往往都会伴随着深度学习的发生.学生提出的问题或许有些比较显而易见，但仔细思考却也是丰富多彩，关键在于弄清学生为什么会提出这样的问题，这个问题可以怎样解决，学生能获得什么.波利亚在《怎样解题》中指出：解决问题包括弄清题意、拟定计划、执行计划和回顾.深度学习的过程就是帮助学生享受这一过程，享受成功解决问题的快乐；享受山重水复疑无路，柳暗花明又一村的惊喜；享受知识本身所散发的独特魅力.