对比教材 改进教学——以“事件的相互独立性”为例

广东 蒋海榕

2017课标版人教A版高中数学教材与2007版人教A版对比，“事件的相互独立性”内容提前并升级.旧教材以条件概率为背景来研究事件的“独立性”，而新教材通过归纳推理抽象出事件的“独立性”.本文从探究概念、深挖内涵、正确判断、巩固应用四个方面对新教材中的“事件的独立性”进行教学探讨.

一、问题的提出

1.新旧教材内容的差异

为了落实立德树人的根本任务，提高学生学科核心素养，在新课程标准背景下，2017课标版人教A版高中数学教材(以下统称“新教材”)投入使用.与2007版人教A版教材(以下统称为“旧教材”)对比，内容编排发生了很大改变.尤其是“概率”部分，新教材中“样本空间”的引入，带来了整章的知识重构.具体见下图：

2017课标版人教A版必修二第十章2007版人教A版选修2-3第二章10.1随机事件与概率10.1.1有限样本空间与随机事件10.1.2事件的关系与运算10.1.3古典概型10.1.4概率的基本性质10.2事件的相互独立性10.3频率与概率10.3.1频率的稳定性10.3.2随机模拟2.1离散型随机变量及其分布列2.1.1离散型随机变量2.1.2离散型随机变量的分布列2.2二项分布及其应用2.2.1条件概率2.2.2事件的相互独立性2.2.3独立重复试验与二项分布2.3离散型随机变量的均值与方差2.3.1离散型随机变量的均值2.3.2离散型随机变量的方差2.4正态分布

从上图我们可以看到：对比旧教材，新教材把“事件的相互独立性”从选修提前到了必修内容，由“2.2二项分布及其应用”下的子目录升级为“10.2事件的相互独立性”单独一节.最为重要的是新教材对事件的相互独立性这一节进行了知识重构，旧教材中是在学习了条件概率基础上，利用条件概率进行演绎推理，研究相互独立的两个事件的概率关系.新教材中并未学习条件概率，是通过两个试验探究，进行归纳推理得出结论.目前大部分关于“事件的相互独立性”教学研究都是以条件概率为背景，无法真正领会新教材编写意图.

2.学生认知的障碍

学生在学习“独立性”之前，就容易对非独立的两个事件的积事件的概率进行乘法运算；判断两个事件是否独立时，学生又容易与前面学的互斥事件发生混淆，甚至会认为可以感性判断两个事件是否独立，不需要独立性公式来判断.

下面从探究概念、深挖内涵、正确判断、巩固应用四方面对新教材中“事件的相互独立性”进行教学探讨.

二、教学探讨

1.巧用探究，引出概念

探究1：分别抛掷两枚质地均匀的硬币，A=“第一枚硬币正面朝上”，B=“第二枚硬币反面朝上”

探究2：一个袋子中装有标号分别是1，2，3，4的4个球，除标号外没有其他差异.采用有放回方式从袋中依次任意摸出两球，设A=“第一次摸到球的标号小于3”，B=“第二次摸到球的标号小于3”

探究3：将探究2中“有放回”改为“不放回”，分别计算P(A)，P(B)，P(AB)，你有什么发现？

设计意图：探究1和探究2来源于课本，探究环节从最简单、学生最熟悉的情境入手.让学生利用前面所学的有限样本空间和古典概型的知识，发现共性，得到结论P(AB)=P(A)P(B)，为归纳出“独立性”概念做准备.

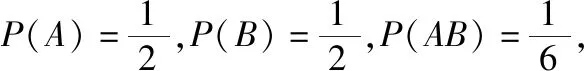
补充的探究3让学生体会概率中两个基本事件有可能满足独立性，但是并非所有的两个事件具备独立性.改变了试验条件，两个事件的关系也发生改变.通过探究3，让学生理解“独立性”，避免在后面学习中滥用公式.这一过程旨在培养学生归纳推理能力与严谨的数学思维.

2.抽象概念，深挖内涵

通过归纳探究1和探究2，得出概念：对任意的两个事件A与B，如果P(AB)=P(A)P(B)成立，则称事件A与B相互独立，简称独立.

探究4：必然事件Ω、不可能事件∅与任意事件相互独立吗？为什么？

探究6：“独立”与“互斥”等价吗？

探究7:设样本空间Ω={a，b，c，d}含有等可能的样本点，且A={a，b}，B={a，c}，C={a，d}.A，B，C三个事件两两独立，P(ABC)是否等于P(A)P(B)P(C)？

设计意图：探究4中，因为P(Ω)=1，所以P(AΩ)=P(A)=P(A)P(Ω)，同理可得P(∅A)=P(A)P(∅)，符合“独立性”的定义.同时，再次让学生理解：事件A的发生与不发生对不可能事件与必然事件发生的概率不产生任何影响.从严谨的概念再回到感性体会，让学生深刻理解独立性的含义.探究5中，类比集合运算，课本给出了详细的推导过程.帮助学生熟悉概率的运算，进一步理解事件的相互独立性的性质.

探究4与探究5，新教材利用独立性的定义“P(AB)=P(A)P(B)”，将问题很好地解决了，不依赖于条件概率，反倒降低了“独立性”学习的难度，这是新教材编排的优点.

设事件A与事件B互为互斥事件，则有P(AB)=0，易得在P(A)>0，P(B)>0的条件下P(AB)≠P(A)P(B).所以得到结论：P(A)>0，P(B)>0的条件下互斥的两个事件一定不具有相互独立性.探究6从定义的角度出发，让学生经历“独立”与“互斥”的概念辨析过程，理解它们是完全不同的概念.

3.善用例题，正确判断

【例1】甲、乙两名射击运动员进行射击比赛，甲的中靶概率为0.8，乙的中靶率为0.9,求下列事件的概率：(1)两人都中靶;(2)恰好有一人中靶;(3)两人都脱靶;(4)至少有一人中靶.

答案：(1)0.72 (2)0.26 (3)0.02 (4)0.98

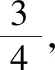
【例3】一个家庭有n(n≥2)个小孩，假设生男孩和生女孩机会均等，事件A表示“有男孩也有女孩”，事件B表示“最多有一个女孩”

(1)当n=2时，事件A与事件B是否独立？

(2)当n=3时，事件A与事件B是否独立？

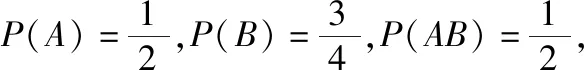
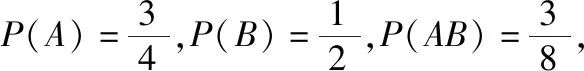
设计意图：例1和例2来源于课本，例1学生可以直接判断两个事件相互独立，例2题目直接告知两个事件独立.这是最简单常见的两种判断情形，要求学生根据独立性的概率公式准确作答.例1和例2的设置，容易让学生觉得，“独立性”都是可以感官直接判断的.例3的补充，可以让学生体会到：P(AB)=P(A)P(B)才是真正能够判断两个事件是否相互独立的条件.再次让学生深刻体会“独立性”的内涵，以此培养学生严谨的思维习惯.

4.活用真题，巩固应用

【练习】(2021·新高考Ⅰ卷·8)有6个相同的球，分别标有数字1，2，3，4，5，6，从中有放回的随机取两次，每次取1个球，甲表示事件“第一次取出的球的数字是1”，乙表示事件“第二次取出的球的数字是2”，丙表示事件“两次取出的球的数字之和是8”，丁表示事件“两次取出的球的数字之和是7”，则

( )

A.甲与丙相互独立

B.甲与丁相互独立

C.乙与丙相互独立

D.丙与丁相互独立

答案：B

设计意图：从历年的高考真题我们可以看到，事件的相互独立性是概率模块考查的重点内容.不管旧教材还是新教材，利用“独立性”进行概率计算始终是要求重点掌握的.特别值得一提的是2021年新高考Ⅰ卷第8题，利用P(AB)=P(A)P(B)判断事件的“独立性”，并不需要依赖条件概率，着重体现了“独立性”定义的优点，与新教材编排意图完全相符.