非对称氧掺杂对石墨烯/二硒化钼异质结肖特基势垒的调控*

郝国强 张瑞† 张文静 陈娜 叶晓军 李红波‡

1)(华东理工大学材料科学与工程学院,上海 200237)

2)(中国科学技术大学化学与材料科学学院,合肥 230026)

在纳米逻辑器件中,制造低的肖特基势垒仍然是一个巨大的挑战.本文采用密度泛函理论研究了非对称氧掺杂对石墨烯/二硒化钼异质结的结构稳定性和电学性质的影响.结果表明石墨烯与二硒化钼形成了稳定的范德瓦耳斯异质结,同时保留了各自的电学特性,并且形成了0.558 eV 的n 型肖特基势垒.此外,能带和态密度数据表明非对称氧掺杂可以调控石墨烯/二硒化钼异质结的肖特基接触类型和势垒高度.当氧掺杂在界面内和界面外时,随着掺杂浓度的增大,肖特基势垒高度都逐渐降低.特别地,当氧掺杂在界面外时,n 型肖特基势垒高度可以降低到0.112 eV,提高了电子的注入效率.当氧掺杂在界面内时,n 型肖特基接触转变为欧姆接触.平面平均电荷密度差分显示随着掺杂浓度的增大,界面电荷转移数量逐渐增多,导致费米能级向二硒化钼导带底移动,证实了随着氧掺杂浓度增大肖特基势垒逐渐降低,并由n 型肖特基向欧姆接触的转变.研究结果将对基于石墨烯的范德瓦耳斯异质结肖特基势垒调控提供理论指导.

1 引言

石墨烯作为典型的二维材料,不仅具有优异的物理强度与比表面积,并具有较高的载流子迁移率与热导率[1,2],因此在能源、催化等多个领域都有广泛应用,如应用在电极修饰、化学电源与传感器等方面.然而,石墨烯带隙为零,电子空穴易复合且光吸收弱,严重阻碍了它在电子与光电子器件应用领域的发展.类石墨烯化学式为MX2的二维过渡金属硫族化物(transition metal dichalcogenides,TMDs),具有半导体的特性[3],此外,TMDs 还具有带隙性质可控、带隙宽度可调的优势,这使它在逻辑电路与光检测器等方面有较好的发展.二硒化钼作为TMDs 的一种材料,不仅具有光学、电学特性与禁带宽度可调等特点[4],相对于常见的二硫化钼,它呈现出了更窄的带隙、更好的电子空穴分离[5]以及在环境中更强的抗氧化性[6]等优点.在超薄的二硒化钼薄膜上制造的背栅场效应晶体管(fieldeffect transistor,FET),实现了高达106的开关比[7].但是,二硒化钼的载流子迁移率偏低,所制备的器件性能有一定的不足.因此将二者结合并获得性能更为优异的异质结是当前主流方法之一.

常见的结合方式为范德瓦耳斯异质结,这类异质结对晶格匹配要求小,也就意味着材料组合空间大,在构建新一代纳米电子器件方面有极大的优势.不同于传统的金属/半导体异质结界面存在有化学紊乱现象与较强的费米钉扎效应[8-10]而限制了异质结发展的情况[11],二维异质结因其表面较少的悬挂键和层间较弱的范德瓦耳斯力可以很好的避免这些缺点.此外,异质结层间中的电荷具有较高迁移速率,和层内载流子寿命相比,层间载流子的寿命大了一个数量级[12],光电导增益大大增加.制备的范德瓦耳斯异质结除了保持二维材料固有的电学特性,还增添了新的电学特性[13,14].将单层二硒化钼与石墨烯进行叠加,构建石墨烯/二硒化钼异质结,其肖特基接触特性极大地弥补石墨烯在整流方面的劣势.

目前,石墨烯/二硒化钼异质结已成功制备,Sata 等[15]通过将机械剥离的石墨烯转移到二氧化硅衬底上,再以过干转移法将二硒化钼薄片转移至石墨烯表面,并使用标准电子束光刻和电子束蒸发添加钛电极,成功制备出了石墨烯/二硒化钼范德瓦耳斯异质结,并且该异质结具有105的大电流开关比和大于103A/cm2的电流密度的优异性能.能否对二维范德瓦耳斯异质结的肖特基势垒进行调控,一定程度地改变某些特性以更好地符合需求,则成了研究的重点.目前,已有Vu 等[13]通过改变外加电场强度,有效地调节了石墨烯/碲硒化钨范德瓦耳斯异质结,使p 型肖特基接触向n 型或欧姆接触发生转变.此外,还有Sun 等[16]在石墨烯/二硒化钼/石墨烯夹层异质结施加垂直应力改变层间距,发现应力迫使二硒化钼将电子传向石墨烯,改变了肖特基接触类型.在改变异质结原子组成方面,Hu 等[17]最近首次提出了非对称掺杂的概念.研究人员对石墨烯/二硫化钼异质结进行了硒掺杂,发现随着界面内硒掺杂浓度的增大,肖特基势垒从n 型转变为p 型,还可以实现小的p 型肖特基势垒.作为一种新型的调控手段,石墨烯/二硒化钼异质结非对称掺杂杂质原子对其肖特基接触特性的影响目前还没有被报道过.通常在制备单层二硒化钼过程中,可能会出现氧化现象,氧原子和硒原子属同族,但氧原子与硒原子的电负性相差较大,氧原子的引入可能会影响异质结的电学性质.

为此,建立了二维石墨烯/二硒化钼异质结模型,采用密度泛函理论研究了非对称氧掺杂对肖特基接触类型和肖特基势垒高度的影响,讨论不同氧掺杂浓度与氧原子所处位置对肖特基势垒的调控,深入分析了掺杂调控机理,为未来设计和制造基于二硒化钼的高性能场效应晶体管具有重要的指导意义.

2 模型和计算方法

采用基于密度泛函理论(density function theory,DFT)的程序包(cambridge sequential total energy package,CASTEP)[18]对石墨烯/二硒化钼结构进行计算.使用广义梯度近似(generalized gradient approximation,GGA)中的Perdew-Burke-Ernzerhof (PBE)方法[19]来描述交换关联泛函,相比于局域密度近似(local density approximation,LDA),PBE 方法在晶体结合能、键长键角和电子亲和能的计算中更接近实验结果.同时引入超软赝势(ultrasoft pseudopotential,USP)进行几何优化和能量计算.由于DFT 中缺乏对长程作用的描述,即对以范德瓦耳斯作用为主的弱相互作用体系描述不佳,引入Tkatchenko-Scheffler (TS)对DFT进行色散校正[20],校正后的DFT-TS 方法即可用于计算层间的范德瓦耳斯相互作用.选取C-2s22p2,Mo-4d55s1和Se-4s24p4价电子组态描述价电子和离子的作用.几何优化和能量计算的截断能设置为380 eV,布里渊区采用2×2×1 的k-point网格,自洽场的收敛精度设置为2×10—5eV/atom,力场收敛精度为0.1 eV/Å (1 Å=0.1 nm),最大应力为0.1 GPa,最大位移不超过0.01 Å.

首先构建石墨烯和单层二硒化钼的原胞(空间点群:P63/mmc),并进行了几何优化,优化后的石墨烯和二硒化钼原胞晶格常数分别为a=2.46 Å和a=3.28 Å,与石墨烯和二硒化钼的晶格常数实验值接近(石墨烯原胞和二硒化钼原胞分别为2.47 Å[21]和3.29 Å[22]).之后构建4×4 的石墨烯超胞和3×3 的单层二硒化钼超胞,以及5×5 的石墨烯超胞和4×4 的单层二硒化钼超胞;在超胞和异质结的垂直方向,即z轴方向上,施加了20 Å的真空以避免相邻周期材料之间的相互影响.为了得到晶格失配率低的模型,计算了这两种情况下的石墨烯/二硒化钼异质结模型的晶格失配率,晶格失配率通过石墨烯晶格常数a1和单层二硒化钼晶格常数a2计算得到,即(a1—a2)/a1,由此计算发现,4×4 的石墨烯超胞和3×3 的单层二硒化钼超胞(图1(a)),以及5×5 的石墨烯超胞和4×4 的单层二硒化钼超胞(图1(b)),其晶格失配率分别为0.06%和6.25%.使用前者构建异质结时,晶格失配率为0.06%,十分微小,可以认为晶格失配对异质结构电学性质影响可以忽略不计[23,24].故选用4×4 的石墨烯超胞和3×3 的单层二硒化钼超胞为周期的模型进行堆叠形成异质结构(图1(a)),作为石墨烯/二硒化钼异质结模型.

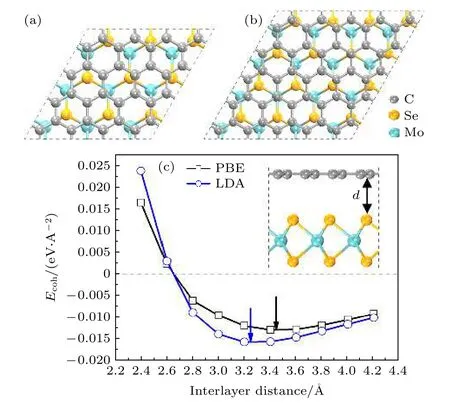
图1 (a)石墨烯4×4 超胞和二硒化钼3×3 超胞组成的异质 结俯视 图;(b)石墨烯5×5 超胞 和二硒 化钼4×4 超胞组成的异质结俯视图;(c)PBE 和LDA 两种 方法 下层间距与石墨烯/二硒化钼异质结结合能的关系.两个箭头表示两种方法下最低能量时的层间距Fig.1.(a)Top views of heterostructure composed of 4×4 lateral periodicity of graphene and 3×3 lateral periodicity of MoSe2 monolayer;(b)top views of heterostructure composed of 5×5 lateral periodicity of graphene and 4×4 lateral periodicity of MoSe2 monolayer;(c)dependence of Ecoh in graphene/MoSe2 heterostructure on the interlayer distance under LDA and PBE methods.The two arrows indicate the d with the lowest Ecoh for LDA and PBE methods.

3 结果与讨论

3.1 结构与稳定性

石墨烯/二硒化钼异质结存在较小的失配率,为了定量分析石墨烯/二硒化钼异质结的失配情况,计算了晶格失配能,按(1)式计算[25]:

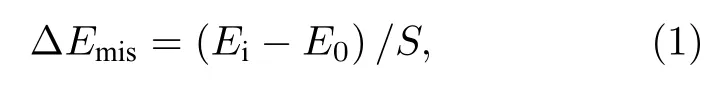
式中,Ei代表石墨烯/二硒化钼异质优化结构中石墨烯和二硒化钼的能量加和,E0代表独立石墨烯和独立二硒化钼优化后的能量加和,S为异质结面积.故晶格失配能为1.96 meV/Å2,可见异质结失配可以忽略不计[26].

为判断石墨烯/二硒化钼异质结的结构稳定性,引入结合能Ecoh,按(2)式计算[27]:

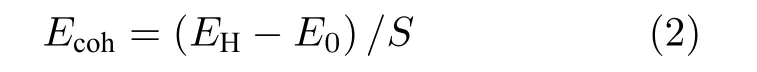
式中,EH为石墨烯/二硒化钼异质结优化后的总能量,图1(c)显示了LDA 和GGA 中PBE 两种函数下Ecoh和层间距的关系,预测的平衡状态下层间距离分别为3.23 Å和3.42 Å,实验中得到石墨烯/二硒化钼异质结的层间距为3.4 Å[28],可见采用PBE 方法更接近实验值,因此本文采用PBE 方法预测结构性能,计算得到Ecoh为—12.72 meV/Å2.结合能为负值,说明在实验中可以形成稳定的石墨烯/二硒化钼异质结[29].

为进一步确认层间作用力是否为范德瓦耳斯作用,引入范德瓦耳斯能进行定量描述.范德瓦耳斯能定义为

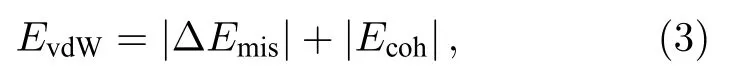
计算得EvdW=14.68 meV/Å2,与Hu 等[25]和Bjoerkman 等[30]计算的范德瓦耳斯异质结的能量相近;同时石墨烯/二硒化钼异质结中平衡状态下层间距为3.42 Å,这与其他实验和理论计算中石墨烯基范德瓦耳斯异质结的数据接近,如石墨烯/二硫化钼[31,32]和石墨烯/氧化锌[33]等.这说明在石墨烯/二硒化钼异质结中,石墨烯与二硒化钼层间作用力为弱的范德瓦耳斯作用.

3.2 能带结构

为了深入了解石墨烯/二硒化钼异质结的电学性质,计算了石墨烯、单层二硒化钼和石墨烯/二硒化钼异质结的能带结构,结果如图2 所示.图2(a)中石墨烯为零带隙结构,狄拉克点附近的能带结构呈现线性色散关系,具有金属特性,这与实验结论一致[34].单层二硒化钼为直接带隙,见图2(b),禁带宽度Eg为1.52 eV,这与Zhao 等[35]通过光致发光(photoluminescence spectroscopy,PL)方法测出的单层二硒化钼禁带宽度(1.57 eV)和Sun 等[16]理论计算的结果(1.547 eV)接近,说明本文使用的计算方法适用于石墨烯/二硒化钼异质结的理论计算.图2(c)为石墨烯/二硒化钼异质结能带结构图,可以看出石墨烯在费米能级附近的线性色散和二硒化钼的直接带隙结构基本没有受影响,推测这是由于该异质结之间的结合力为弱的范德瓦耳斯力.与独立的单层二硒化钼相比,异质结中二硒化钼的禁带宽度仍为1.52 eV,并且导带底和价带顶的位置仍然处于G点,只是费米能级发生了移动,从原来位于价带顶向导带底移动.从图2(c)可以看出,相比于二硒化钼的价带底,费米能级离导带底更近,因此异质结中二硒化钼呈现n 型半导体特性.

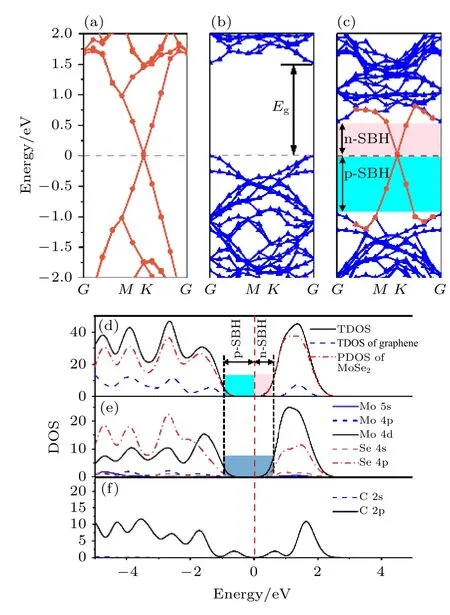
图2 能带结构图 (a)石墨烯;(b)单层二硒化钼;(c)石墨烯/二硒化钼异质结.(d)石墨烯/二硒化钼异质结的总态密度和分态密度;(e)异质结中二硒化钼的分态密度;(f)异质结中石墨烯的分态密度.费米能级设置为零,用红色虚线表示Fig.2.Band structures of (a)graphene;(b)MoSe2 monolayer;(c)graphene/MoSe2 heterostructure;(d)total density of states (DOS)and partial density of states (PDOS)of graphene/MoSe2 heterostructure;(e)PDOS of MoSe2 in the heterostructure;(f)PDOS of graphene in the heterostructure.The Fermi level is set to zero,denoted as a red dashed line.

为了更好探究平衡状态下石墨烯/二硒化钼异质结的能带结构组成,对其进行态密度(total density of states,DOS)和分态密度(partial density of states,PDOS)的计算,如图2(d)—2(f)所示.可以得到该异质结中二硒化钼的导带底部和价带顶部的形成主要与Mo 4d 轨道和Se 4p 轨道有关,石墨烯对该异质结的贡献则体现在费米能级附近.此外,将二硒化钼的导带底(conduction band minimum,CBM)与费米能级的能量差定义为n 型肖特基势垒高度(n-type Shottky barrier height,n-SBH),价带顶(valence band maximum,VBM)与费米能级的能量差定义为p 型肖特基势垒高度(ptype Shottky barrier height,p-SBH),从图2(c)和图2(d)可以看出,n-SBH ＜ p-SBH,因此石墨烯/二硒化钼异质结呈现出n 型肖特基接触特性,这与能带结构分析结果相同.同时图2(e)中可以得到,在二硒化钼导带中Mo 4d 和Se 4p 形成了杂化轨道,在价带中,没有杂化轨道的形成.导带中杂化轨道的形成有益于Mo 4d 轨道上的激发态电子跃迁到Se 4p 轨道,从而使得电子集中在石墨烯/二硒化钼异质结界面的Se 原子处.

为了探究形成石墨烯/二硒化钼异质结能带结构变化的机理,对其进行功函数的计算.功函数的数值大小反映电子逸出的难易程度,表达式为

式中,Evac和EF分别代表真空能级和费米能级,计算结果如图3 所示,可以看出二硒化钼的功函数高于石墨烯,异质结的功函数在石墨烯和二硒化钼功函数之间.二硒化钼的VBM 和CBM 带边位置EVB和ECB相对于标准氢电极(normal hydrogen electrode,NHE)分别为1.40 V 和—0.12 V.在图3(d)中,当形成异质结时,为了达到平衡状态,石墨烯的部分电子转移到二硒化钼表面,使得电子在异质结二硒化钼内表面聚集,由此形成了从石墨烯指向二硒化钼的内建电场Ein,在界面处产生了电子势垒,阻止了电子从石墨烯到单层二硒化钼的扩散,使得电子的扩散和漂移运动达到平衡.因此,二硒化钼的费米能级向负方向移动,石墨烯的费米能级向正方向移动,直到其费米能级一致,形成了一个向上的能带弯曲(Δ=0.16 V),最终形成了一个n 型肖特基势垒.

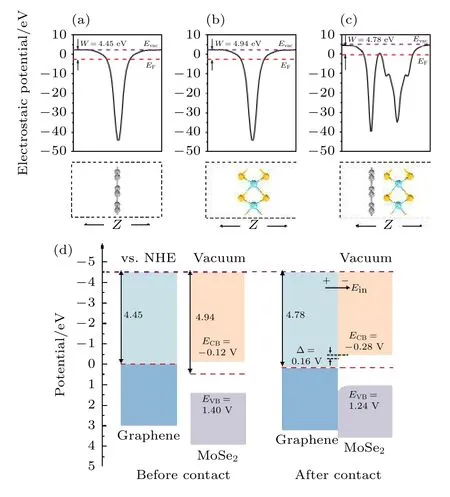
图3 静电势 (a)石墨烯;(b)单层二硒化钼;(c)石墨烯/二硒化钼异质结(红色和紫色虚线分别代表费米能级和真空能级);(d)石墨烯和单层二硒化钼接触前和接触后的带边位置图Fig.3.Electrostatic potentials of (a)graphene;(b)MoSe2 monolayer;(c)graphene/MoSe2 heterostructure(red and purple dashed lines represent the Fermi level and vacuum level,respectively);(d)energy level lineup diagrams for graphene and MoSe2 monolayer before and after contact.

计算异质结的三维电荷密度差分,石墨烯和二硒化钼形成异质结后,界面电荷进行了重新分布,电荷密度公式为

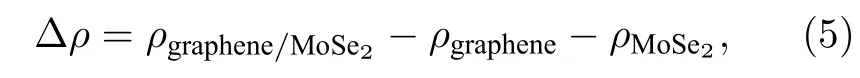
其中,ρgraphene/MoSe2,ρgraphene和ρMoSe2分别代表石墨烯/二硒化钼异质结、石墨烯和二硒化钼的电荷密度,计算如图4 所示,蓝色和粉色区域分别代表电子的消耗和聚集.从图4(a)和4(b)中可以看出,二硒化钼接触界面的硒原子层上各硒原子点处电子分布较均匀,基本呈标准馕状,而石墨烯处的空穴则随超胞内二硒化钼分布的变化而呈现聚集与分散.图4(c)中可以看出,当形成异质结时,为了达到平衡状态,石墨烯的部分电子转移到二硒化钼表面,使得电子在异质结二硒化钼内表面聚集,由此形成了从石墨烯指向二硒化钼的内建电场,在界面处产生了电子势垒,阻止了电子从石墨烯到单层二硒化钼的扩散,使得电子的扩散和漂移运动达到平衡.这一现象可以解释之前所述的二维异质结中单层二硒化钼的能带移动.同时对石墨烯/二硒化钼异质结的电荷密度进行了Mulliken 布居分析,可以得出石墨烯到二硒化钼表面电子转移量为0.04e,这也与图4(c)中石墨烯表面电子消耗,二硒化钼内表面电子积累现象相符.

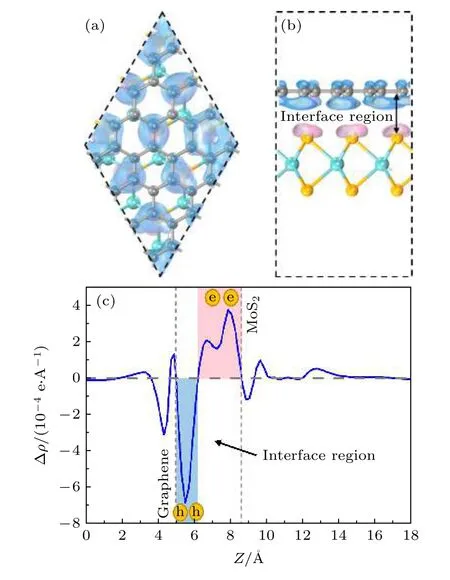
图4 石墨烯/二硒化钼异质结的三维电荷密度差分 (a)俯视图;(b)侧视图;(c)石墨烯/二硒化钼异质结的平面平均电荷密度差分Fig.4.Three-dimensional charge density difference diagram of graphene/MoSe2 heterostructure:(a)Top view and (b)side view;(c)plane-averaged charge density difference of graphene/MoSe2 heterostructure.

3.3 肖特基调控

在石墨烯/二硒化钼异质结(Gr/MoSe2(1—x)O2x)中,采用非对称氧掺杂对异质结的肖特基势垒进行调控,二硒化钼中单侧的硒原子被不同浓度的氧原子随机取代,氧原子浓度分别为11% (x=0.056),22% (x=0.111),33% (x=0.167),44% (x=0.222),56% (x=0.278),67% (x=0.333),78% (x=0.389),89% (x=0.444)和100% (x=0.500),因此非对称氧掺杂的异质结划分为氧原子在异质结界面内和界面外两种类型.表1 表明,随着氧掺杂浓度的增大,MoSe2(1—x)O2x的晶格常数a逐渐减小,这主要是由于钼氧键的键长较钼硒键的短.从而异质结的晶格失配率随界面内和界面外氧掺杂浓度增大而增加.当氧掺杂浓度在78%及以下时,MoSe2(1—x)O2x与石墨烯之间的晶格失配率小于5%,反之晶格失配率大于5%,构建的Gr/MoSe2(1—x)O2x异质结在实际制备中较难实现[17],因此本文主要讨论氧掺杂浓度小于等于78%的情况[36].首先对掺杂氧的MoSe2(1—x)O2x进行几何结构优化,然后与石墨烯形成异质结后,再对Gr/MoSe2(1—x)O2x异质结进行几何结构优化,优化后异质结如图5 所示.

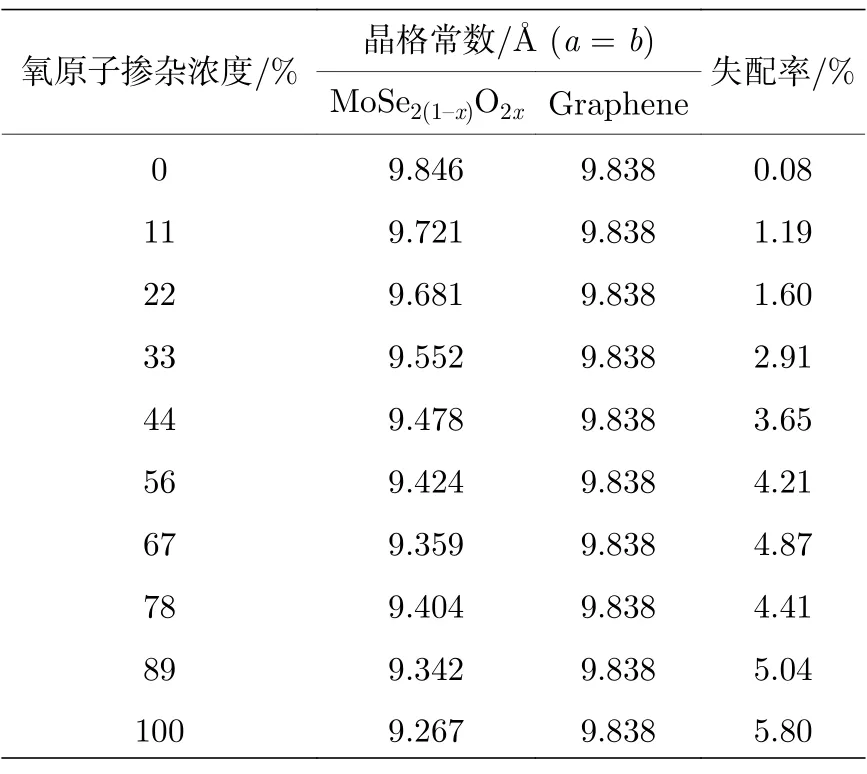
表1 不同氧原子掺杂浓度的Gr/MoSe2(1—x)O2x异质结失配率Table 1.Mismatch ratio of Gr/MoS2(1—x)O2x heterosstructure with different oxygen doping concentration.

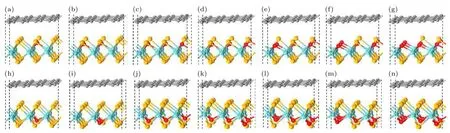
图5 不同掺杂浓度的Gr/MoSe2(1—x)O2x 异质结侧视图 (a)-(g)对应界面内氧掺杂浓度分别为11%,22%,33%,44%,56%,67%和78%;(h)-(n)对应界面外氧掺杂浓度分别为11%,22%,33%,44%,56%,67%和78%.浅蓝色,黄色,灰色和红色的球分别表示钼,硒,碳和氧原子Fig.5.Side views of the Gr/WSe2(1—x)O2x heterostructures with different concentrations of the oxygen dopant:(a)-(g)show the O doping on the inner interface are 11%,22%,33%,44%,56%,67% and 78%,respectively.(h)-(n)represent the oxygen doping on the outer interface are 11%,22%,33%,44%,56%,67% and 78%,respectively.The light blue,yellow,grey and red balls represent Mo,Se,C and O atoms,respectively.

异质结的能带结构在掺杂下会发生一定变化,为了使该异质结能更好用于逻辑电路,使用非对称氧掺杂手段对其进行调控,异质结几何结构优化后能带结构计算如图6 所示.当掺杂发生在界面内时,随着氧掺杂浓度的增大,费米能级向导带底靠近,肖特基势垒高度逐渐降低,肖特基接触类型为n 型.当氧掺杂浓度高于56%时,肖特基接触转变为欧姆接触.当掺杂发生在界面外时,随着氧掺杂浓度的增大,费米能级同样向导带底靠近,靠近趋势相对于界面内掺杂更为缓和,肖特基接触类型一直保持n 型,没有形成欧姆接触,当氧掺杂浓度达到最高时,肖特基势垒高度达到了非常小的水平.

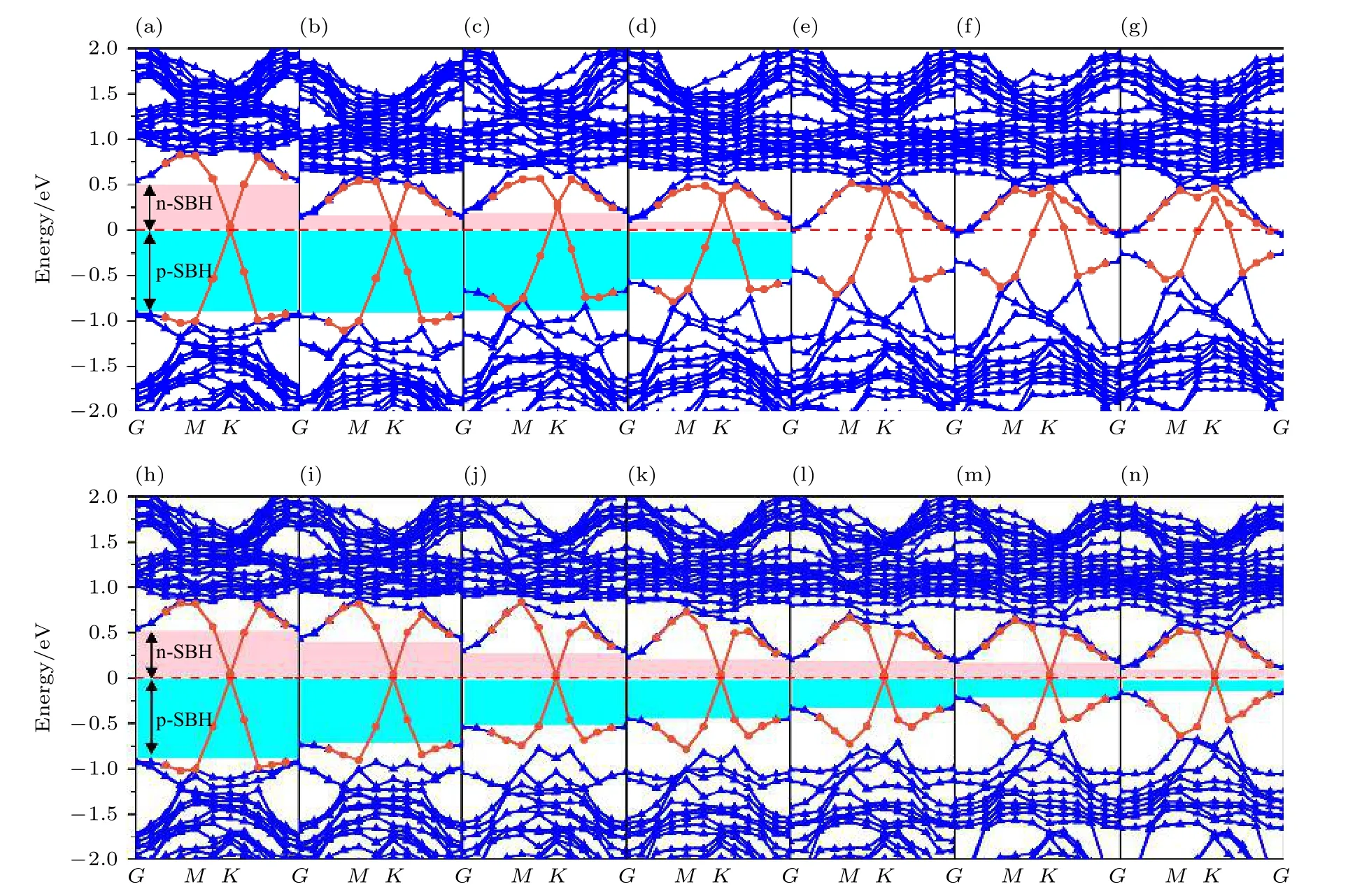
图6 不同氧掺杂浓度下Gr/MoSe2(1—x)O2x 异质结的能带结构图 (a)-(g)对应界面内氧掺杂浓度分别为11%,22%,33%,44%,56%,67%和78%;(h)-(n)对应界面外O 掺杂浓度分别为11%,22%,33%,44%,56%,67%和78%.费米能级用红色虚线标记,并设置为零Fig.6.The band structures of the Gr/MoSe2(1—x)O2x heterostructure under asymmetric oxygen doping:(a)-(g)Show the oxygen doping on the inner interface are 11%,22%,33%,44%,56%,67% and 78%,respectively;(h)-(n)represent the oxygen doping on the outer interface are 11%,22%,33%,44%,56%,67% and 78%,respectively.The Fermi level is marked with a dashed red line and set to zero.

在分析能带结构时,提到了肖特基势垒高度的变化,对肖特基势垒做出定量分析.根据金属/半导体界面处的肖特基-莫特模型可知[9],n 型肖特基势垒高度ΦBn与p 型肖特基势垒高度ΦBp的表达式为

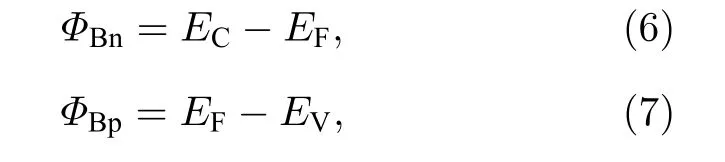
式中,EF为费米能级能量,EC为导带底能量,EV为价带顶能量.肖特基接触类型与肖特基势垒高度以ΦBn与ΦBp中较小者进行判定,而二维材料的带隙约为ΦBn和ΦBp之和.肖特基势垒高度计算如图7(a)所示,在未掺杂时,肖特基接触类型为n 型,ΦBn为0.558 eV.随着氧掺杂浓度的提高,所有曲线总体都呈下降趋势.当氧掺杂在界面内时,氧浓度以11%的间隔,从11%增加到78%,ΦBn依次为0.544 eV,0.141 eV,0.207 eV,0.101 eV,0 eV,0 eV 和0 eV;当氧掺杂在界面外时,同样得到ΦBn依次为0.544 eV,0.435 eV,0.304 eV,0.226 eV,0.202 eV,0.112 eV 和0.105 eV.从ΦBn变化中可以清楚看到异质结肖特基接触类型的变化,可以发现,当界面内氧浓度大于等于56%时,Gr/MoSe2(1—x)O2x异质结形成了欧姆接触.同时,随着氧掺杂浓度的提高,MoSe2(1—x)O2x的带隙宽度逐渐降低,说明氧原子不仅降低肖特基势垒高度,也降低了MoSe2(1—x)O2x的带隙宽度.另外,计算了非对称氧掺杂下Gr/MoSe2(1—x)O2x异质结的功函数,如图7(b)所示,当氧掺杂在界面内时,随着氧掺杂浓度的增大,功函数从4.78 eV 显著降低到3.96 eV,当氧掺杂在界面外时,功函数随着氧掺杂浓度的增大而增大,当浓度大于56%时,功函数呈现较微弱降低,因此Gr/MoSe2(1—x)O2x异质结的功函数大小依赖于氧掺杂浓度和掺杂位置.

由于对石墨烯/二硒化钼异质结进行了非对称氧掺杂,层间因范德瓦耳斯力相互作用使界面电荷再次发生了排布,我们对异质结平面平均电荷密度差分进行了计算以揭示电荷在MoSe2(1—x)O2x和石墨烯上发生的积累和转移.电荷密度差分为

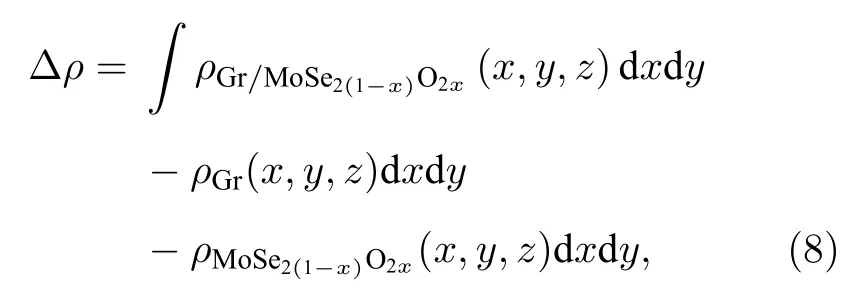
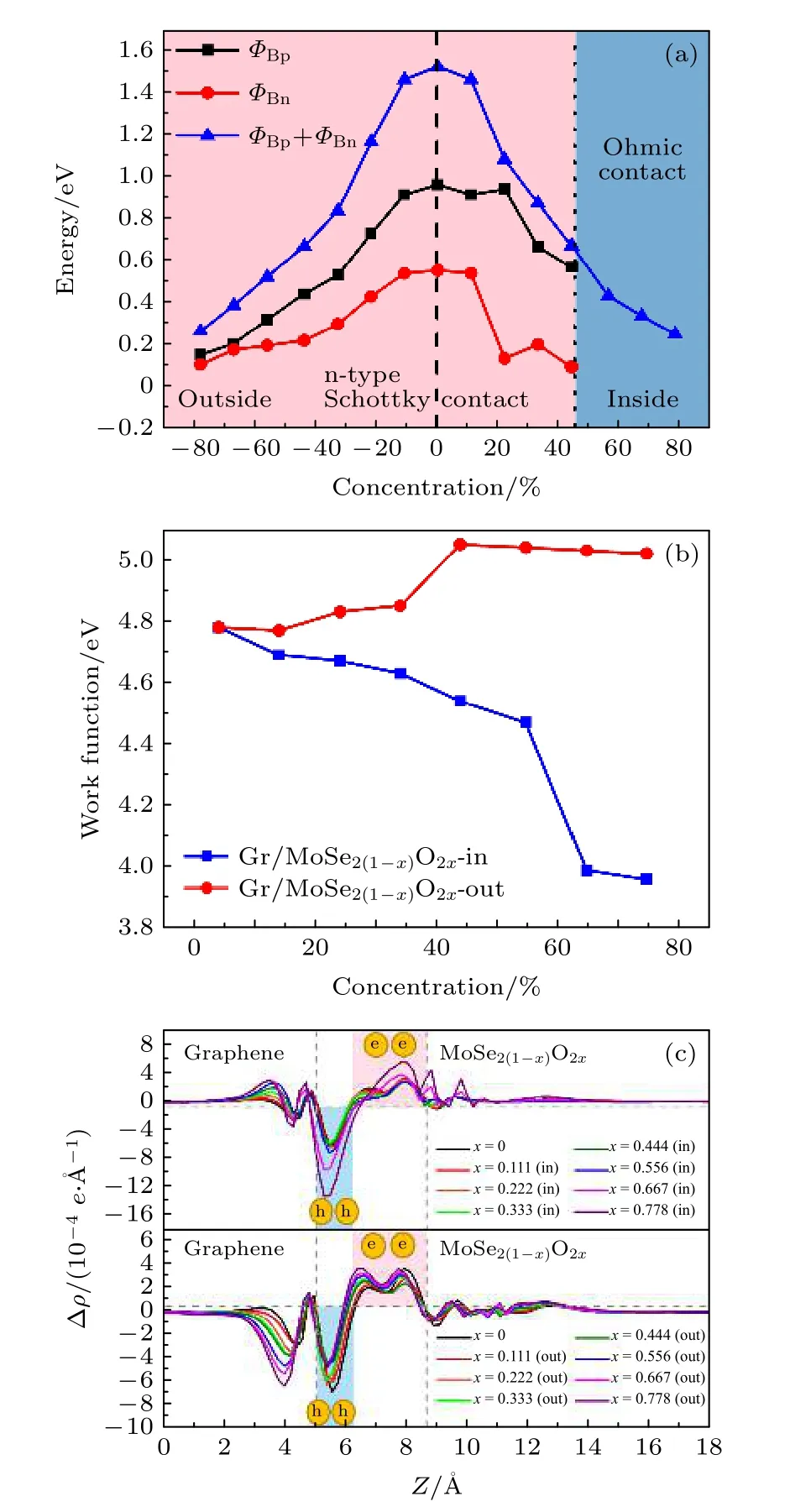
图7 不同氧掺杂浓度下 (a)Gr/MoSe2(1—x)O2x 异质结的肖特基势垒高度;(b)Gr/MoSe2(1—x)O2x 异质结的功函数;(c)Gr/MoSe2(1—x)O2x 异质结沿着Z 方向氧掺杂在内表面和外表面的平面平均电荷密度差分图Fig.7.Dependence of (a)the SBH and (b)work function in Gr/MoSe2(1—x)O2x heterostructure on the oxygen doping concentration;(c)calculated planar electron density differences of the Gr/MoSe2(1—x)O2x heterostructure along the Z direction in different oxygen doping concentrations inside and outside the interface.

4 结论

通过将石墨烯与单层二硒化钼垂直叠加,得到了稳定的范德瓦耳斯石墨烯/二硒化钼异质结,并且二者保留了各自的固有特性,同时形成了n 型肖特基接触.利用密度泛函理论系统地探索了非对称氧掺杂在降低石墨烯/二硒化钼异质结的肖特基势垒高度的有效性.结果表明,氧掺杂的引入不仅可以降低肖特基势垒高度,而且还可以将n 型肖特基接触转变为欧姆接触.此外,通过界面电荷的再分布分析可得出,形成异质结后,电子从石墨烯向二硒化钼转移,形成了从石墨烯指向二硒化钼的内建电场,在界面处产生了电子势垒,阻止了电子从石墨烯到单层二硒化钼的扩散.同时随着氧掺杂浓度的增大,电子转移量逐渐增多,解释了肖特基势垒高度降低的机理,该研究对改善基于二硒化钼的纳米场效应晶体管电学性能提供了一种有效的方法,为制备高性能纳米场效应晶体管提供了理论指导.