可压缩液体中气泡的声空化特性*

郑雅欣 那仁满都拉

(内蒙古民族大学数理学院,通辽 028043)

利用新提出的Gilmore-NASG 模型,在考虑液体可压缩效应的边界条件下,研究了可压缩液体中气泡的声空化特性,并与利用原有KM-VdW 模型计算得到的结果进行了比较.结果表明,相比于KM-VdW 模型,由于Gilmore-NASG 模型采用新的状态方程来描述气体、液体以及由可压缩性引起的液体密度变化及声速变化,所以用Gilmore-NASG 模型得到的空化气泡的压缩比更大、崩溃深度更深、温度和压力峰值更高.随着驱动声压幅值的增大,两种模型给出的结果差别愈加明显,而随着驱动频率的增大,两种模型给出的结果差别逐渐减小.这表明,在充分考虑泡内气体、周围液体在不同温度和压强下共体积的变化所导致的介质可压缩特性下,气泡内的温度和压强可能达到更高值.同时,Gilmore-NASG 模型还预测出了气泡壁处液体的密度变化、压力变化、温度变化以及液体中的声速变化.因此,Gilmore-NASG 模型在研究高压状态下气泡的空化特性以及周围液体对气泡空化特性的影响方面具有优点.

1 引言

对于可压缩液体中的声空化气泡,通常使用的气泡动力学方程有Keller-Miksis[1](KM)方程和Gilmore[2]方程,两者都是利用连续介质力学的基本运动方程,在气泡壁处液体马赫数的一级近似下简化得到[3-7].但两种方程简化时采用的条件有所不同,KM 方程中认为气泡周围液体密度和声速是常量,而Gilmore 方程中认为液体密度和声速是随液体压力变化的量.KM 方程应用于声致发光及声化学问题的研究表明,此方程在低驱动声压下较为准确[8,9].因为在高驱动声压下,气泡剧烈崩溃时产生的泡壁速度可以超过液体中的恒定声速,导致气泡壁处液体马赫数异常增大,这就违背了KM 方程所基于的小马赫数假设.Gilmore 方程则考虑了液体密度变化以及由此导致的声速变化,这有效地降低了气泡剧烈崩溃时气泡壁处液体马赫数瞬间变得很大的可能,所以Gilmore 方程更适合于研究高驱动声压下的声空化问题[10-12].由于KM 方程中认为气泡壁处液体密度和声速是恒定不变的,所以通常与van der Waals (VdW)状态方程结合构成KM-VdW 模型[13,14].Gilmore 方程中认为液体密度和声速是随液体压力变化的量,所以通常与Tait 状态方程结合构成Gilmore-Tait 模型[2,15,16].Tait 状态方程可以描述诸如水这样的液体介质的可压缩性,给出了介质密度与压力之间的变化关系,但它不能直接预测介质的温度,也不能反映介质热容的影响,且Tait 方程中的多方指数选取得异常大,不符合热力学关系[17].这说明,需要一种更合适的状态方程来描述液体介质的可压缩性以及由此引起的密度变化和声速变化[18-20].最近,Denner[21]把Gilmore 方程与Noble-Abel-Stiffend-Gas (NASG)状态方程相结合,提出了一种新模型,即Gilmore-NASG 模型,并与传统的Gilmore-Tait 模型进行了比较.从两种模型对预测气泡壁处液体温度的结果来看,Gilmore-Tait 模型给出的气泡壁处液体温度高于气泡内的温度,这是错误的结果,说明Tait 状态方程自身有所缺欠.另外注意到,目前研究气泡空化问题时在气泡壁处采用的压力边界条件,多数情况下都是只考虑液体切变黏滞影响,未考虑液体体积黏滞影响的边界条件.由Navier-Stokes 方程以及黏性应力张量可知[4],当液体不可压缩时,其速度的散度为零,此时体积黏滞系数相关的黏滞应力为零,这导致体积黏滞作用对气泡壁的运动不会产生影响;只有液体可压缩时,其速度的散度不为零,体积黏滞作用才会对气泡壁的运动有影响[22].因此,研究可压缩液体中气泡空化时,为体现液体的可压缩性,应使用包含切变粘滞作用和体积粘滞作用的边界条件.

为了充分体现液体可压缩性,本文将利用新提出的Gilmore-NASG 模型,在考虑液体可压缩效应的边界条件下,数值研究可压缩液体中空化气泡的声空化特性,并把结果与KM-VdW 模型给出的结果进行比较分析.

2 气泡动力学模型

2.1 Gilmore-NASG 模型

Denner[21]把Gilmore 方程与NASG 状态方程相结合,提出了Gilmore-NASG 模型[10].经典的Gilmore 方程为

式中,R=R(t)为气泡瞬时半径,点表示对时间的导数,H为液体在泡壁处和无穷远处焓的差,Cl为液体中的声速.此模型采用一种新的状态方程,即NASG 状态方程[20]来统一描述气泡内气体、蒸气和气泡外液体的状态.NASG 状态方程可表示为

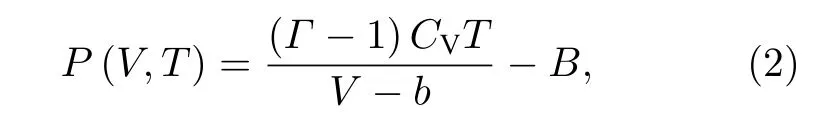
式中,P为压力;T为温度;CV为热容;Γ为多方指数;V为比容,与密度ρ的关系为V=1/ρ;B为压力常数,表示分子吸引效应;b为共体积(分子所占体积),表示分子排斥效应.相比于其他状态方程,NASG 状态方程能够统一描述气相、液相以及气液共存相,且满足热力学关系[18].由于考虑了介质热容的影响,所以能够准确预测气、液介质的温度.此外,状态方程(2)中的共体积b和压力常数B是根据实验饱和曲线,在不同温度和压力下取点计算确定的,所以更能够准确反映分子排斥效应和吸引效应[20].

利用状态方程(2),在不考虑传质传热的绝热情况下,把液体的焓差和液体中的声速可表示为

而常数kl和驱动声压Pex(t)为

同时,泡内压力Pg、泡内温度Tg及泡壁温度Tl可表示为

2.2 KM-van der Waals 模型

KM-VdW 模型是KM 方程与VdW 状态方程相结合得到的,其中KM 方程为

由VdW 状态方程得到的泡内压力Pg及泡内温度Tg的表达式为

(13)式—(15)式中,m为气体摩尔数,V为气泡体积,其他量与Gilmore-NASG 模型中所代表的含义相同.以上各式中,下角标“l”表示液体相关量,“g”表示气体相关量,“∞”表示无穷远处的量,“0”表示静态或环境量.

2.3 气泡壁处压力边界条件

用KM-VdW 模型计算气泡空化问题时,由于认为气泡壁处液体密度和液体中的声速都是不变的常量,所以通常使用不考虑液体可压缩效应的边界条件[23,24],这也是合理的.然而,在Gilmore-NASG模型中认为气泡壁处液体密度和液体中的声速都是随压力变化的,即认为气泡壁处液体是可压缩的,所以采用考虑液体可压缩效应的边界条件更合适.为此,本文采用(16)式表示的考虑液体可压缩效应的边界条件[25]:

式中σ,η,λ分别代表液体的表面张力系数、切变黏滞系数、体积黏滞系数.当等号右边的最后一项等于零时,方程(16)就变成我们熟悉的不考虑液体可压缩效应的边界条件.

3 数值模拟

选择水为液体介质,泡内气体为氩气,气泡初始半径R0=4.5 µm,驱动声压振幅A=1.4 atm,频率f=30 kHz.两种模型相关的物理参数如表1和表2所列.Gilmore-NASG 模型中参数Bl和bl的计算方法以及液体、气体环境参数的选取可参考文献[17,20,26].关于泡内气体分子共体积,两种模型所使用的值不同.在NASG 状态方程中,在不同的温度和压力下,气体分子共体积有不同的取值.本文使用的氩气共体积是根据文献[27,28]给出的计算方法,在温度为20000 K 时计算得到的值.VdW 状态方程中的参数a和b,通常认为是不随温度和压力变化的常量,本文选取文献[29]给出的值,具体计算时取a=0,这是为了与NASG 方程中Bg=0对应.为了方便描述,下面用模型Ⅰ和模型Ⅱ分别代表Gilmore-NASG 模型和KMVdW 模型.

表1 Gilmore-NASG 模型中水和氩气的相关物理参数Table 1.Physical parameters of water and argon in Gilmore-NASG model.

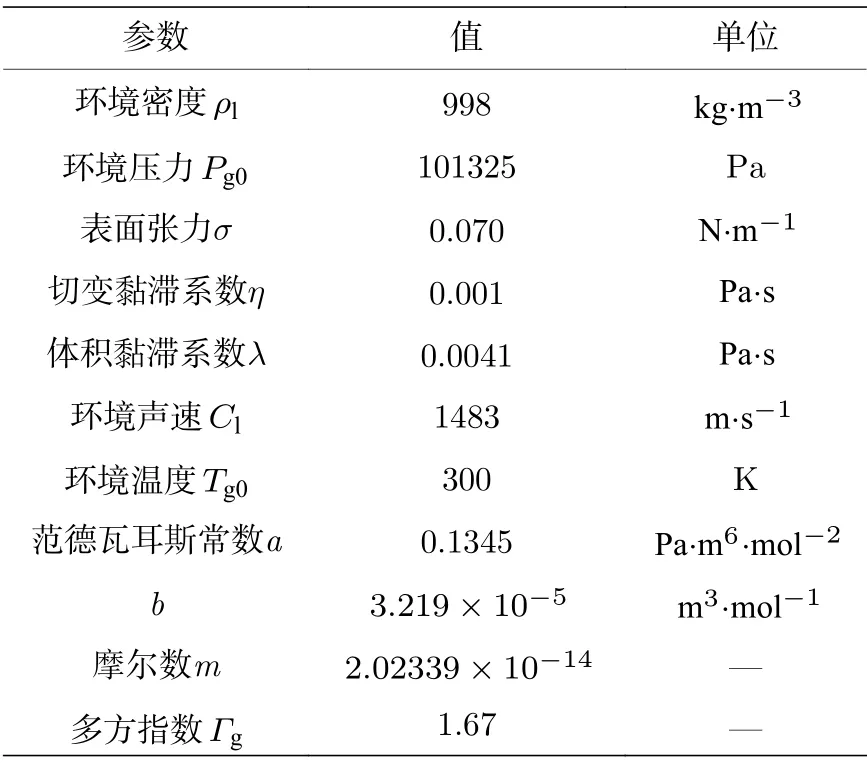
表2 KM-VdW 模型中水和氩气的相关物理参数Table 2.Physical parameters of water and argon in KM-VdW model.

3.1 可压缩液体中氩气泡的空化特性

本节研究在一定强度和一定频率的超声波作用下,可压缩水中氩气泡的空化特性.用模型Ⅰ计算了空化气泡的半径变化、速度变化、泡内压力变化、温度变化以及气泡壁处液体的密度变化、压力变化、温度变化、声速变化、马赫数变化,并与用模型Ⅱ得到的结果进行了比较,结果如图1 所示.从图1(a)可以看出,气泡的膨胀过程是一个相对缓慢的过程,在此过程中两种模型给出的气泡半径变化并无明显差别,由此可知在膨胀阶段液体可压缩性对气泡空化行为的影响很小.从气泡第一次崩溃时的最小半径的对比可看出(图1(a)插图),模型Ⅰ给出的气泡最小半径更小,即有着更大的压缩比.出现这种现象的主要原因是,两种模型中使用的状态方程不同,所选用的泡内气体分子共体积(bg)和泡壁处液体分子共体积(bl)不同.模型Ⅰ中采用NASG 状态方程统一描述气泡内气体和气泡壁处液体,充分考虑气泡内气体的可压缩性,认为不同温度和压强下气体分子共体积应取不同值,在高温高压下气体分子共体积要小于VdW 状态方程中的气体分子共体积(bg＜b),共体积小意味着气体被压缩的空间更大,所以气泡的崩溃深度更深(即最小半径更小).同时,NASG 状态方程中充分考虑了气泡壁处液体的可压缩性对气泡崩溃行为的影响,即考虑了液体分子共体积的影响.液体分子共体积大,意味着液体分子之间的排斥作用强,液体不易被压缩,所以气泡壁处液体对于气泡的压力大,使气泡崩溃得更深.自然,崩溃深度越深的气泡,泡内气体压力越大(如图1(c)),所以气泡回弹的速度也越大(如图1(b)),这就导致模型Ⅰ给出的气泡第一次崩溃后的回弹半径比模型Ⅱ给出的回弹半径更大(如图1(a)).这与文献[15,26]给出的结果相同.图1(c)和图1(d)给出的是气泡内压力(Pg)和气泡壁处液体压力(Pl)的变化,可以看出,模型Ⅰ给出的Pg和Pl峰值均明显高于模型Ⅱ给出的值,这种差距主要是由两种模型给出的气泡崩溃深度不同引起的,模型Ⅰ给出的气泡崩溃深度更深,所以模型Ⅰ给出的Pg和Pl峰值更大.比较Pg和Pl可知,模型Ⅰ给出的Pg峰值高于Pl峰值约0.3 MPa,模型Ⅱ给出的Pg峰值高 于Pl峰值约0.8 MPa.图1(e)和图1(f)给出的是气泡壁处液体密度变化和液体中声速变化,可看出模型Ⅰ给出的液体密度和液体中的声速在气泡崩溃时明显增大,这是由于气泡崩溃时气泡壁处液体压力发生变化(图1(d))所导致.这一点从液体密度公式(5)和液体中的声速公式(4)也可直接看出.与模型Ⅰ给出结果相比,模型Ⅱ给出的液体密度和液体中的声速都是常数(图中黑虚线表示).由此可看出,模型Ⅰ更充分体现了液体的可压缩性.两种模型预测出的泡内温度变化如图1(g)所示.可以看出,模型Ⅰ预测出的泡内温度高于模型Ⅱ预测出的温度,可达21250 K,该温度值比较接近于安宇[30]预测出的水中氩气泡的泡内温度.模型Ⅰ还预测出了气泡壁处液体的温度变化(图1(h)),但模型Ⅱ不能预测气泡壁处液体的温度变化.模型Ⅰ预测出的气泡崩溃时的液体最高温度约为430 K,实际上在绝热过程中气泡壁处液体温度不应该达到此值(已高于环境温度300 K),所以可理解为气泡壁处液体温度的上限.图1(i)为两种模型给出的马赫数对比,可以看出模型Ⅰ给出的马赫数峰值明显小于模型Ⅱ给出的马赫数峰值,这是因为模型Ⅰ中认为液体中的声速是随压力变化的,所以气泡崩溃瞬间气泡壁的速度很大时液体中的声速也变得很大,这样就有效地降低了气泡壁处液体马赫数瞬间变得很大的可能,保证了模型Ⅰ的有效性.不管是KM 方程还是Gilmore 方程都是在小马赫数假设条件下简化得到,所以只有在小马赫数条件下两种方程才能保证它们的有效性.

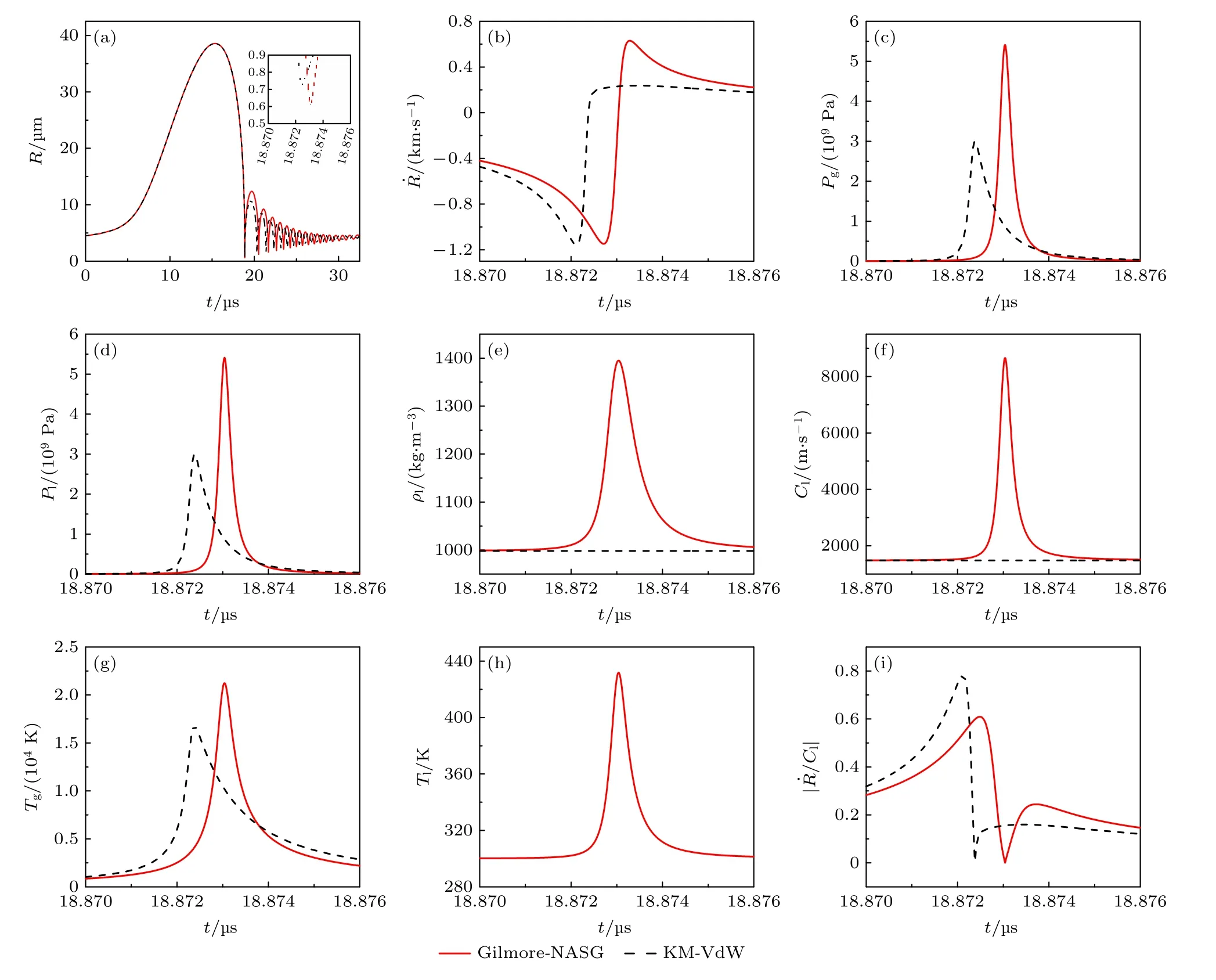
图1 (a)气泡半径变化;(b)气泡壁速度变化;(c)气泡内压力变化;(d)气泡壁处液体压力变化;(e)气泡壁处液体密度变化;(f)气泡壁处液体中声速变化;(g)气泡内温度变化;(h)气泡壁处液体温度变化;(i)气泡壁处液体马赫数变化Fig.1.(a)Change of bubble radius;(b)change of bubble wall velocity;(c)change of pressure in the bubble;(d)change of liquid pressure at the bubble wall;(e)change of liquid density at the bubble wall;(f)change of sound velocity in the liquid at the bubble wall;(g)change of temperature in the bubble;(h)change of liquid temperature at the bubble wall;(i)change of liquid Mach number at the bubble wall;.

3.2 驱动声压对可压缩液体中氩气泡空化特性的影响

本节主要考察驱动声压变化对可压缩液体中氩气泡空化特性的影响.利用模型Ⅰ和模型Ⅱ,在驱动频率不变的情况下分别计算了气泡最大半径、最小半径、崩溃速度、回弹速度、泡内最大压力、泡内最高温度以及气泡壁处液体最大马赫数,结果如图2 所示.可以看出,随着驱动声压幅值的增加,两种模型给出的气泡最大半径均逐渐增大(图2(a)),气泡最小半径均逐渐减小(图2(b)),气泡压缩比均呈增大趋势,这与文献[31]所得结果相同.相比较,两种模型给出的气泡最大半径变化基本相同,最小半径变化出现了明显的差异,模型Ⅰ给出的气泡最小半径更小,即气泡崩溃得更深,并且随着驱动声压幅值的增大,两种模型给出的气泡最小半径的差异逐渐增大,这结果与文献[15,26]所得结果相同.从图2(c)可以看出,随着驱动声压幅值的增大,气泡崩溃速度和回弹速度均逐渐增大.相比可知,两种模型给出的气泡崩溃速度差别不大,但回弹速度出现了明显差别,模型Ⅰ给出的回弹速度更大,这可以导致气泡回弹半径更大.对比两种模型给出的最大马赫数(图2(d))可知,随着驱动声压幅值的增大,两种模型给出的最大马赫数都在增大,但模型Ⅱ给出的最大马赫数相比于模型Ⅰ增大得更多.这表明,模型Ⅰ更适合于研究高驱动声压下的声空化问题.两种模型给出的泡内最大压力和泡内最高温度,随驱动声压幅值的增大而变化情况,如图2(e)和图2(f)所示.可以看出,随着驱动声压幅值的增大,泡内最大压力和最高温度都在增大,比较而言,模型Ⅰ预测出的泡内最大压力和最高温度增大得非常明显.综上可知,随着驱动声压幅值的增大,两种模型给出的结果差别愈加明显,模型Ⅰ对高压状态下气泡空化行为的描述更加显现.

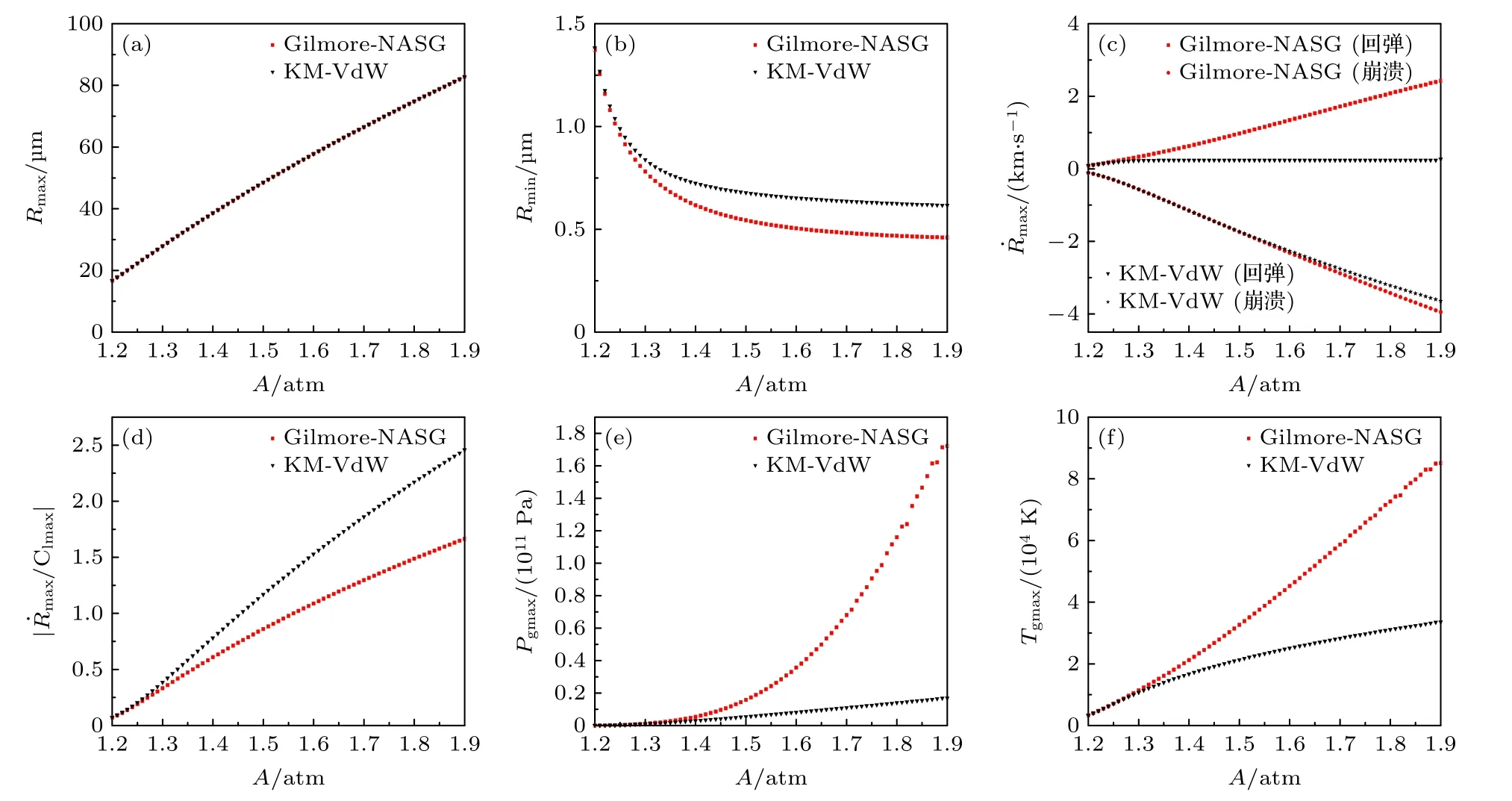
图2 (a)气泡最大半径、(b)最小半径、(c)崩溃速度和回弹速度、(d)液体最大马赫数、(e)泡内最大压力以及(f)泡内最高温度,随驱动声压幅值的变化Fig.2.(a)Maximum bubble radius,(b)minimum radius,(c)collapse speed and rebound speed,(d)maximum liquid Mach number,(e)maximum pressure in the bubble,and (f)maximum temperature in the bubble change with amplitude of driving sound pressure.

3.3 驱动频率对可压缩液体中氩气泡空化特性的影响

本节在驱动声压幅值不变的条件下,主要考察驱动频率变化对可压缩液体中氩气泡空化特性的影响.利用模型Ⅰ和模型Ⅱ,分别计算了气泡最大半径、最小半径、崩溃速度、回弹速度、泡内最大压力、泡内最高温度以及气泡壁处液体最大马赫数,结果如图3 所示.从图3(a)和图3(b)可以看出,随着驱动频率的增大,两种模型给出的气泡最大半径减小,最小半径增大,气泡压缩比均呈减小趋势,与文献[15,23]所得结果一致.主要原因是随着驱动频率的增大,气泡膨胀及压缩周期相对缩短[26,32],气泡没有足够的时间膨胀到更大和压缩至更小.两种模型给出的气泡最大半径无明显差别,最小半径有明显差别,随着驱动频率的增大差别逐渐减小,并出现高频激励下趋于一致的走向.两种模型给出的气泡崩溃速度和回弹速度(图3(c))的差别也随驱动频率的增大而减小,并出现逐渐趋于一致的规律.随着驱动频率的增大,两种模型给出的最大马赫数(图3(d))、泡内最大压力(图3(e))和泡内最高温度(图3(f))均出现逐渐趋于一致的规律.总体上,随着驱动频率的增大,两种模型给出的结果差别逐渐减小,并出现高频激励时趋于一致的规律.

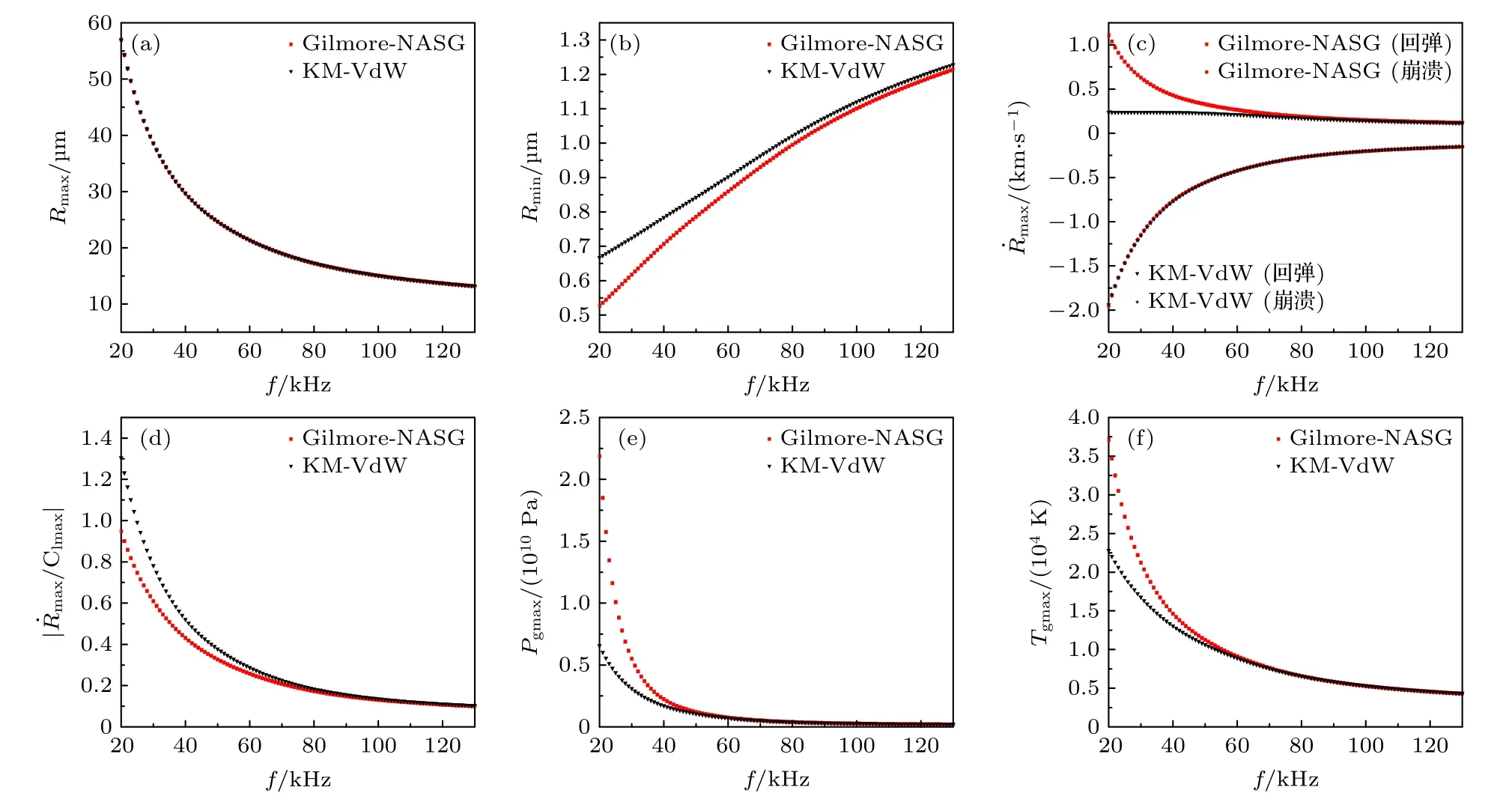
图3 (a)气泡最大半径、(b)最小半径、(c)崩溃速度和回弹速度、(d)液体最大马赫数、(e)泡内最大压力 以及(f)泡内最高温度随驱动频率的变化Fig.3.(a)Maximum bubble radius,(b)minimum radius,(c)collapse speed and rebound speed,(d)maximum liquid Mach number,(e)maximum pressure in the bubble,and (f)maximum temperature in the bubble change with driving frequency.

4 结论

本文研究了可压缩水中氩气泡的声空化特性.为充分体现气泡内气体和周围液体的可压缩性,采用了Gilmore 方程与NASG 状态方程相结合的新模型,并在气泡壁处采用了考虑液体可压缩效应的边界条件.NASG 状态方程能够统一描述气泡内气体、蒸气以及周围液体在不同温度和压强下的状态,能够充分体现介质分子排斥效应和吸引效应,可以准确表达气、液介质密度变化和压强变化,能够考虑到介质的热容效应,可以准确预测气、液介质的温度变化.在不考虑气泡内气体与周围液体之间的质量交换、热交换和化学反应的情况下,相比于KM-VdW 模型给出的结果,用Gilmore-NASG模型计算得到的空化气泡的压缩比更大,崩溃深度更深,温度和压力峰值更高.随着驱动声压幅值的增大,两种模型给出的结果差别愈加明显,而随着驱动频率的增大,两种模型给出的结果差别逐渐减小.这表明,在充分考虑泡内气体、周围液体在不同温度和压强下共体积的变化所导致的介质可压缩特性下,气泡内的温度和压强可能达到更高值.Gilmore-NASG 模型还能准确地预算出气泡壁处液体的密度变化、压力变化、温度变化以及液体中的声速变化,但KM-VdW 模型不能预算这些量的变化.这一优势对于研究周围液体对气泡空化特性的影响非常重要.总体而言,Gilmore-NASG 模型在高压状态下对气泡空化特性的研究以及周围液体对气泡空化特性影响的研究方面具有优势,在高强度聚焦超声、冲击波碎石治疗以及声化学等具体问题的研究中将会有重要应用.