融入课程思政的高等数学教学的探索与实践
2022-01-19陈艳平
陈艳平
(福建商学院 信息工程学院,福建 福州,350102)
习近平总书记在全国高校思想政治工作中明确提出,“其他各门课都要守好一段渠、种好责任田,使各类课程与思想政治理论课同向同行,形成协同效应”,要“把思想政治工作贯穿教育教学全过程,实现全程育人、全方位育人,努力开创我国高等教育事业发展新局面”[1]。2017年12月,教育部发布《高校思想政治工作质量提升工程实施纲要》,提出“大力推动以‘课程思政’为目标的课堂教学改革”,“实现思想政治教育与知识体系教育的有机统一”[2]。高等数学是高等学校经济类、管理类本科专业学生必修的一门重要的学科基础课,是学生树立良好的学习习惯和养成良好的学习动力的重要基础课程,对于培养和提高学生的创新能力与综合素质起着极为重要的作用。从教学实践出发,探索将高等数学知识传授、能力培养和价值引领相结合,并产生协同增效的作用。
关于高等数学课程思政教学的探讨,以“高等数学”“课程思政”为关键词,在中国知网学术期刊库上进行检索,相关论文成果有260余篇,多数是从高等数学的数学文化角度探讨课程思政的必要性、可行性和可操作性,鲜有见到从案例教学视角探讨课程思政与学科素养之间的关系。本文从提高学科素养角度探索高等数学课程思政的方法,以起到抛砖引玉的作用。
一、坚持以课堂为基础,发挥课堂-教师-学生的作用
(一)以课堂为基础,发挥课堂教学“主渠道”作用
高等数学课程思政是把高等数学的理性、应用性与课程思政的感性、人文性相结合,教师从知识、能力、素养这三个维度,探索多样化的教学方法设计,运用问题驱动、启发式、探究式、讨论式、翻转课堂等教学方式,减少学生对高等数学的恐惧感,激发其学习的兴趣与主动参与度。创新运用现代化教育手段,利用智能化教学平台和智慧教学工具,利用国家级教学资源,建设独立SPOC课程,开展线上与线下混合式教学,打破时空限制,确保教学目标的实现。不断推进课程思政教育教学改革,寻找思政元素无痕浸润到数学知识中的案例。以社会主义核心价值观为引领,在传授专业知识、培养综合能力和养成数学素养等基本功能的基础上,实现知识传授、能力培养与价值引领功能的有机统一。
(二)构建教师良好的数学人生观,发挥教师队伍“主力军”作用
《高等数学》教学普遍存在的问题是内容多、课时少、学生入学门槛低、数学基础参差不齐、学习能力差异大等,怎么让学生在课堂上坐得住、听得进、学得会是每一位高等数学任课教师面临的艰巨任务[3]。课程思政是方法不是“加法”[4]。高等数学课程本身具备与课程思政有机融合的独特优势,怎样让这些元素落地、生根、开花、结果,关键是教师思政。“学生入耳入脑入心,首先要求老师入耳入脑入心。”教师要加强自身知识储备并实现自我更新,才能提高教师的视角站位。数学教师要明确高等数学课程思政是什么?为什么要做?做什么?怎么做?提高数学教学的品质,要发挥教师队伍“主力军”作用。小学知事,中学明理,大学求道。传道授业是帮助学生拥有学习生存的技能和手段;解惑是帮助学生树立健全的人格,是生存之根本。因此,数学教师拥有良好的数学人生观,才能以身作则、为人师表、立德树人,学生才愿意跟随教师的思路深入思考探求数学的奥秘。数学教师的视角站位要足够高,并拥有良好的数学和文化素养,才能引导学生从多个角度深入研究数学问题,指导学生在学习中获得数学智慧,启发学生将数学智慧外溢,获得在其他领域有益的启示。
(三)创建学生良好的人生价值观,发挥学生的主体作用
以学生为中心,数学教学应该是数学思维活动的教学,教师起导航仪的作用。学生是否理会导航仪的语音提示,是否能按提示正确操作,另辟蹊径的做法是否可行,都需要学生来完成或检验。学生要学会自主学习,并会独立思考,能从已有的知识框架出发,在新旧知识冲突碰撞中推动思维活动,把冰冷美丽的数学转化为火热的思考,探究解决问题的方法。通过课前、课中、课后的问题引发学生思考。课前发布问题,目的在于指导学生有效的预习;课中提出问题,促进学生新旧知识的碰撞并产生思维火花,引发学生温故而知新;课后提出问题,督促学生思考、巩固、提高、拓展,将课堂教学时空延伸。以知识为载体,创新教学方法,以实例引入概念,结合动态图、思维导图、知识点关系图等淡化理论,借助“互联网+”,遵循循序渐进的认知规律,促使学生在课堂上坐得住、听得进、想得通、悟得透。
二、立足高等数学学科特点,探索高等数学课程思政的切入点
结合数学学科独特的优势,积极挖掘高等数学知识传授中能引发学习者思想、认知、情感上共鸣的思政元素,努力寻求知识体系中与思政知识体系中的“交点”,构建符合社会主义核心价值的“数学观”,从学生熟悉的生活情境触发其对经济社会问题的思考,把学生喜闻乐见的社会热点问题转化为数学问题,让思政理念贯穿学习始终,并与数学知识融会贯通,易于理解、易于认同、易于接受、易于产生同频共振,形成协同效应,从而做到高等数学教学与思想政治教育同向同行,达到显性教育与隐性教育融为一体的良好教育效果,真正做到“立德树人”。
《高等数学》课程内容蕴含丰富的思政元素,主要从以下三个切入点:
(一)家国情怀
例如“极限的思想”,从战国中期庄子的“一尺之锤,日取其半,万世不竭”,到魏晋时期数学家刘微的割圆术“利用圆内接正多边形来推算圆的周长和面积,其方法是随着内接正多边形边数的增加,其周长和面积将越来越接近圆周长和圆面积”,都充分展示了中国古代数学对世界数学的巨大贡献。教师可以充分利用好这些素材,布置课前阅读任务,让学生列出相应数列,并观察这些数列的变化趋势,理解数学极限定义的同时,加深了解这两位数学家,增强学生的民族文化自信。
(二)唯物辩证法
《高等数学》作为一门非数学专业介绍微积分理论的公共核心基础课,其知识体系和逻辑体系融入大量哲学原理和辩证法观点[5],为我们提供了认识世界的辩证唯物主义思想。比如,计算曲边梯形的面积和立体图形的体积,从局部与整体、近似与精确等不同视角研究事物变化的性质,经历“分割、近似、求和、取极限”数学过程,通过极限思想将二者对立地统一起来,揭示定积分概念蕴含“有限与无限”“直与曲”“变与不变”“近似与精确”“量变与质变”等。高等数学课程思政可以将数学哲学唯物辨证史观有机结合到高等数学课程建设的各个环节中。将哲学原理渗透和融入到课堂教学中,要将微分和积分的对立统一规律、微分方程求解的普遍性与特殊性原理、积分与不定积分的内容与形式范畴等知识点的联系润物细无声地融入到知识点的讲授中。
(三)科学方法论
《高等数学》孕育的数学素养为我们提供了改造世界的科学方法论。不论是“化圆为方”“化曲为直”“化无限为有限”“化变为不变”思想方法还是“对立统一”“质量互变”“否定之否定”等辩证唯物主义思想,启示我们在遇到复杂问题时,通过理性的判断、科学的分析、思辨的方法,可以将未知的复杂的问题转化为已知的熟悉的问题,体会“化整为零,积微成著”的方法,反映生活中“化繁为简,积零为整”的思想,培养学生在学习和工作中勇于探索的科学精神、精益求精的工匠精神、不忘初心砥砺前行的奋斗精神。
三、结合高等数学的学科素养,探索高等数学教学与思想政治教育同向同行
高等数学的学科素养,指的是面对社会生活实际问题,能在正确的思想价值观念指导下,合理运用科学的思维方式与方法,有效整合学科相关知识,运用学科相关能力,高质量地认识问题、分析问题、解决问题的综合品质。学科素养体现为理性思维、数学应用、数学探究、数学文化四个方面。
(一)训练理性思维,倡导求真务实的世界观
思维是核心素养的核心。美国哲学家迈克尔·桑德尔说:“学习的本质不在于记住哪些知识,而在于它触发了你的思考”。著名科学家钱学森说:“教育最终的机理在于思维过程的训练。”数学思维即人们通常所指的数学思维能力,即用数学的观点去分析问题、思考问题和解决问题,比如演绎与类比、抽象与概括。数学思维能力主要指会观察、实验、比较、猜想、分析、综合、抽象和概括;会用归纳、演绎和类比进行推理;会合乎逻辑、准确地阐述自己的思想和观点;能运用数学概念、思想和方法辨明数学关系,形成良好的思维品质[6]。培养学生数学的理性思维,倡导具体问题具体分析、实事求是、求真务实的世界观,有助于学生树立正确的人生观。
例1 已知初等函数y=f(x)在其定义域[1,4]上连续, 求f(x2)的连续区间。
【疑惑】f(x2)的连续区间是[-2,-1],[1,2]还是[-2,-1]∪[1,2]?

【备注】“[-2,-1],[1,2]”与“[-2,-1]∪[1,2]”看似没有区别,实际区别很大,这正是数学严谨性的体现,也说明细节决定成败。单调区间含两个及以上的之间也用“和”或者“,”联结,表示在每个区间上分别单调。
【解法】用求最值常用的方法:先求f′(x),再令f′(x)=0,得驻点和不可导点;比较驻点、不可导点、区间端点处的函数值,得最值。但这题求f′(x),计算量很大易错。
去伪存真、化繁为简、化归转化、透过现象看本质的方法是“降维打怪”常用方法,培养学生理性思维的同时能灵活解决问题,还能拓展学生知识面,对提升学生综合能力和终身学习大有裨益,也对培养学生科学严谨、实事求是、求真务实、追求真理的思想品质奠定良好的基础。
(二)实践数学应用,培养与时俱进的时代观
教师在上课过程中,为了让学生增强数学应用的意识,要注意引导学生将经济问题转化为数学问题,让数学思想、研究方法和着眼点更好地帮助学生理解经济问题中的基本概念和重要原理[7]。此外,教师要以学生关注的焦点或社会热点问题为突破口,让学生感受到数学不但来源于现实,而且应用于现实。比如当下的新冠肺炎疫情,学生们亲身感受到疫情对学习、生活和社会造成的影响,如果在数学课堂上单纯讲勤洗手、戴口罩、打疫苗,学生会认为教师为思政而思政,可以结合课程内容,在学习微分方程中,课前布置预习传染病模型以及传染病机理及预防知识,并发布思考题。
【思考题1:如何估计游船上的传染病人数?】
一只游船上有800人,一名游客患了某种传染病,12小时后有3人发病,由于这种传染病没有早期症状,故感染者不能被及时隔离,直升机将在60至72小时之间将疫苗运到,试估算疫苗运到时患此传染病的人数。
【思考题2:永久免疫的传染病扩散问题】
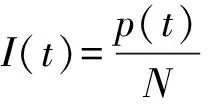
(1)感染者不能痊愈也不能死亡,永远属于p(t);
(2)本地区人的接触均匀,接触即传染,设λ为每个患者每天平均传染他人数。
课堂上,引导学生通过建模求解,让其深刻感悟到及时采取防控措施十分重要。
课后,布置作业:某种传染病第一天只有一个患者,前5天为潜伏期,不发作也不会传染人,第6天开始发作,从发作到治愈需要5天时间,期间每天传染3个人,求第N天共有多少患者。
依托课程内容,培养学生用科学的态度对待疫情,用数学的观点理性看待疫情的产生、发展趋势、打疫苗的重要性及必要性,用数学的方式引导学生科学分析疫情数据并积极投身于当下的疫情防控,用数学的推导证明中国防控政策的正确性,帮助学生树立正确的数学价值观。与时俱进结合当下经济社会生活的热点问题,主动运用数学的理性思维探究经济社会问题,自觉利用数学的思想方法寻求解决经济社会问题,习惯将经济社会问题转化为数学模型,自主借助数学工具解决经济社会问题,会给数学课程思政带来新的突破。
(三)培养数学探究,落实创新的发展观
在数学探究教学中,教师帮助学生“再创造数学”(即引导学生发现结论并给出证明),让学生通过“自主·探究·合作”的方式学习,实现知识的发现、内化、迁移、增值,增强学生的探索能力、合作精神,在传道的同时起到课程思政的作用。数学探究教学不单是讲授数学知识,更重要的是引导学生探索知识、发现知识,感受数学创新(“再创造”)的魅力[8]。基于课程思政的高等数学创新教学,是在相应的知识点下拓展实例与思政结合的教学以促进创新思维的展开,培养学生用发展的思维思考问题并解决问题,是学生树立正确人生观、价值观和世界观的基础。
比如,在闭区间上连续函数性质,课前布置预习。
【思考题3】证明:方程x3-4x2+1=0在区间(0,1)内至少有一个根,并思考该命题有哪些不同的提法。
课堂上引导学生思考,至少有以下不同的提法:
(1)证明方程x3+1=4x2在区间(0,1)内至少有一个根。
(2)证明方程x3+1=4x2至少存在一个正根,且根不超过1。
(3)证明方程x3+1=4x2至少存在一个小于1的正根。
(4) 证明函数f(x)=x3+1-4x2在区间(0,1)有一个不动点,即存在x*,使得f(x*)=x*。
引导学生进一步思考,(1)-(4)与(5)(6)之间的区别与联系,带着这个问题学习,直至得到解答为止。
(5)证明方程x3+1=4x2至少有一个根。
(6)证明方程x3+1=4x2在区间(0,1)内恰有一个根。
布置作业: 设函数f(x)在区间[a,b]上连续, 且f(a)
课后,通过进一步的训练巩固,对形如以下提法的同学加以表扬:
A.设函数f(x)在区间[a,b]上连续, 且b≤f(x)≤a,证明: 存在ξ∈(a,b), 使得f(ξ)=ξ。
B.设函数f(x)在区间[a,b]上连续, 且b≤f(x)≤a,则f(x)在区间[a,b]上至少存在一个不动点。
C.设函数f(x),g(x)在区间[a,b]上连续, 且f(a)
问题设计越来越高级,让学生沉浸在问题变化中,积极思考它们之间的区别与联系,这样学生不仅学到知识,更学到从不同角度看问题的方法,用发展变化的观点看待问题,这种数学思维锻炼会让学生受益终身。
再如,在极限运算的教学中,课前布置预习,发布如下思考题。
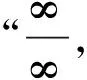

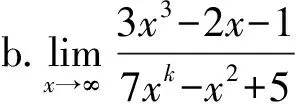


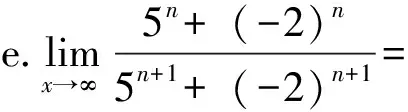
(四)提升数学文化,养成思辨的方法论
知识是数学的身躯,文化是数学的灵魂,在课堂教学中,只讲数学没有文化就失去数学的灵魂,只讲文化没有数学就把数学课变为欣赏课,数学文化让学生受益终身。比如,泰勒级数可以模拟某点已知值附近的函数值:
用sinx的幂级数与多项式逼近之间的关系,举例说明:
作出如下图形,图1:

图1
说明,精确到不同的项,就是不同级的近似。如果课堂上到这里戛然而止,学生会认为数学很难,抽象不易理解,看到图1后,觉得不同级的近似之间的误差太大了,越发迷茫。
当精确到更多项,即有更高阶导数时,如图2:
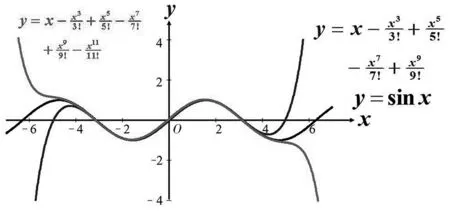
图2
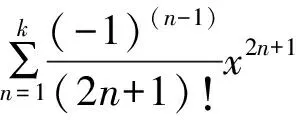
假设f(x)是人生预测曲线。若取f(x)=f(x0),零级近似相当于生帮硬套别人的做法,这种仿效做法得到回报收益可能会与自己的期望大相径庭;取f(x)=f(x0)+f′(x0)(x-x0),一级近似是看到自己和别人的差异,包括优势、劣势、环境、时机等,然后对人生这个函数做最粗略的走势求导(比如钱少是劣势、教育是优势),再综合起来估计自己的回报;二级、三级、乃至N级近似,就要求对人生函数有更多的了解。所谓“世事洞明皆学问,人情练达即文章”,世事越洞明,人情越练达,对人生的认识就越精确,做选择时的预测也就越准确[9]。同时注意到,不同点的近似程度不同,说明时过境迁,要理性地认识世界、改变策略,才能找到相对最好的结果。这种思考升维,学生领悟到用数学的眼光看待问题意义重大。
由于受到高等数学课时的限制,涉及数学文化的内容,可以布置学生课前阅读给学生新鲜感,或课后阅读训练让学生回味。数学文化与课程思政相融合,更能展现高等数学教育的生命力,彰显数学教育的价值引领作用。
四、结语
数学的终极价值不仅在于经世致用,更为理性思辨[10]。将课程思政元素自然融入到高等数学教学中,结合当下社会经济热点问题不断更新教学案例库、不断丰富教学方法、不断完善教学策略,培养学生数学理性思维,强化数学意识,养成辩证思考的能力,让学生学会用数学的眼光看待世界、用数学的方式分析问题、用数学的方法解决问题、用数学的智慧点亮人生。
