动荷载作用下隧道围岩塑性区演化规律研究

张宝永

(中铁十九局集团有限公司 北京 100176)

1 引 言

随着国家经济发展以及社会产能需求量的增加，过去的浅部开采已经不能满足日常生产与生活需要，深部区域资源开采已成为必然趋势。但由于特殊地质条件的原因，深部开采所挖隧道周边应力集中明显，地震、机械振动、爆破、相邻岩爆等动力扰动对围岩稳定性影响极大，极易触发岩爆，导致深部开采的危险系数极高[1－3]，人身安全受到威胁并对国家财产造成重大损失，所以对于岩爆现象预警尤为重要。由于岩石的地质条件及岩爆成因的复杂性，采用试验研究不同动力扰动下隧道围岩稳定性存在着操作困难、数据难以获取、成本高等问题，所以利用数值模拟研究不同动力扰动形式对隧道围岩稳定性的影响有着一定的意义。

为此，国内外部分学者对隧道围岩在动力扰动作用下的稳定性进行了研究。朱万成等[4]利用数值软件系统RFPA模拟不同侧压力系数下动态扰动触发深部围岩巷道失稳破坏的过程；唐礼忠等[5]利用ABAQUS模拟动力扰动作用下不同位置、不同倾角、不同厚度软弱夹层对巷道围岩稳定性的影响；张欣等[6]以青岛胶州湾海底隧道为工程背景，提出了爆破施工荷载作用下隧道顶板厚度设计参考值，并验证其可行性；Zhao，J等[7]将离散元软件与有限差分软件相耦合，对冲击波在节理岩体中的传播规律进行分析；耿萍等[8]利用ANSYS/LS-DYNA软件对穿越不同宽度和倾角断层破碎带的隧道动力响应进行数值计算；吉凌等[9]借助数值模拟与现场测试方法，研究隧道开挖爆破作用下的围岩振动响应特征；刘邦、郭东明、冯春等[10－12]研究了爆炸作用下隧道围岩裂纹起裂与扩展规律。然而，以上研究主要是通过改变动力扰动作用下的参数来分析隧道围岩的稳定性以及在开挖过程中对围岩稳定性的静力分析，并未考虑在开挖过程中的动力扰动对围岩稳定性的影响。

本文利用数值模拟软件模拟隧道在开挖过程中受到正弦波、折线波、梯形波三种不同动力扰动形式下隧道围岩的受力情况，分析不同动力扰动形式、不同作用时间周期、不同应力幅值、不同侧压力系数以及衬砌厚度对隧道围岩塑性区的影响。

2 动力扰动发生失稳破坏数值模拟

2.1 数值模型建立

建立长95 m、宽95 m、深度100 m的隧道围岩模型，如图1所示。在围岩上部和右侧施加均布荷载以考虑初始地应力的影响，在左侧和底端施加固定约束。

所建隧道模型高12 m，宽19 m，计算时将围岩划分成9个区域，对每个区域单独划分网格，为了能准确反映隧道围岩塑性区的变化，对隧道区域进行细化。以折线波形式、梯形波形式、正弦波形式作为3种典型动力扰动波，选取100 MPa、300 MPa和500 MPa作为扰动波幅值，选取0.01 s、0.02 s和0.05 s作为3种不同的时间周期，对不同动力扰动波、不同应力幅值及不同时间周期进行组合，共27组动力扰动波组合形式。

本文利用有限元软件模拟隧道分步开挖过程，数值模拟中围岩及衬砌参数如表1所示。考虑实际工程开挖进展，模拟时选取4 m作为一个开挖步，共25个开挖步。在每个开挖步开始之前加入动力扰动形式，并在每个开挖步结束之后激活对应的衬砌支护。在开挖结束之后，分析不同动力扰动组合形式下隧道围岩的稳定性、围岩塑性区分布情况及变化规律。

表1 围岩和衬砌力学参数

2.2 数值模拟结果

(1)正弦波动力扰动形式的影响

为探究正弦波动力扰动形式作用下隧道开挖过程中围岩塑性区的变化情况，考虑侧压力系数为0.1时，应力幅值及作用时间周期对隧道围岩塑性区的影响。

图2为正弦波作用形式下，应力幅值为100 MPa，作用周期分别为0.01 s、0.02 s、0.05 s的三种动力扰动组合下的隧道开挖结束后洞周塑性区分布图。

图2 不同周期隧道开挖结束后塑性区分布

图3～图4为作用周期为0.01 s时，应力幅值分别为100 MPa、300 MPa及500 MPa所对应的正弦波拱顶位移和应力随开挖步变化曲线。

图3 周期为0.01 s时不同幅值正弦波拱顶位移随开挖步变化曲线

图4 周期为0.01 s时不同幅值正弦波拱顶应力随开挖步变化曲线

正弦波应力幅值为100 MPa时，不同时间作用周期得到的位移分别为0.074 6 m、0.074 7 m、0.074 9 m。由图3、图4可以看出，不同时间周期下的围岩塑性区变化趋势大致相同，均在隧道两侧拱脚和右侧拱顶处出现塑性区，且不同作用时间周期下的围岩塑性区面积相差不大。由此可见，作用周期的长短对围岩塑性区影响不大。

(2)折线波动力扰动形式的影响

折线波作用形式下不同幅值及不同作用时间周期下初始开挖侧隧道顶点的位移和应力分布如图5所示。

图5 折线波组合下位移和应力分步曲线

由图5可知，随着作用荷载逐渐增加，折线波形式作用下动力扰动的初始开挖侧洞顶位移由0.045 m逐渐增大至0.419 m。

在相同作用时间和荷载下，比较正弦波形式下扰动所产生的位移和塑性区的变化情况与折线波形式下扰动所产生的位移和塑性区的变化情况，发现正弦波作用情况下，隧道围岩塑性区的面积大于折线波作用形式下围岩塑性区的面积，说明正弦波形式作用情况下围岩的结构更容易受到破坏。

(3)梯形波加载形式下的影响

不同幅值及不同作用时间周期在梯形波作用形式下初始开挖侧隧道顶点的位移和应力分布如图6所示。

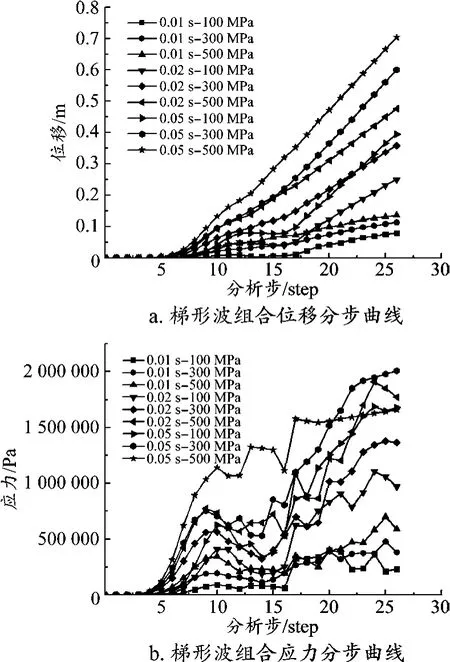
图6 梯形波组合位移和应力分步曲线

由图6可知，随着开挖步的增加，作用荷载增大，梯形波作用形式下隧道初始侧开挖位移从0.079 8 m增至0.436 m。在相同作用时间和应力幅值下，比较正弦波形式下扰动所产生的位移及塑性区变化情况、折线波形式下扰动所产生的位移和塑性区分布情况与梯形波形式下扰动所产生的位移与分布情况，发现梯形波作用形式下位移最大，在隧道两侧拱脚及拱顶都出现塑性区，折线波作用形式下位移最小，塑性区仅在隧道两侧拱脚处出现。如果长时间处于梯形波作用形式下的动力扰动，围岩容易失稳，从而引发灾害。

3 其他因素影响

在工程实际中，侧压力系数不同、衬砌厚度的确定都会对隧道围岩稳定性产生影响，为了研究其影响程度，本文以正弦波形式为例，探究不同侧压力系数及不同衬砌厚度对隧道围岩稳定性的影响。

3.1 侧压力系数对隧道围岩塑性区的影响

为方便分析，在正弦波作用周期为0.01 s、应力幅值为100 MPa的情况下，研究侧压力系数的变化对隧道围岩稳定性的影响。为了考虑不同的初始地应力分布状态，侧压力系数分别取k＝1.0、k＝2.0。

图7为侧压力系数为1.0、2.0时开挖结束后所对应的洞周塑性区分布图。

图7 侧压力系数为1.0、2.0时开挖结束隧道洞周塑性区分布

在k＝1.0时，由于侧压力的增加，会改善之前顶部与底部的受拉情况以及两侧拱脚的受压情况，所以对于隧道塑性区发生改善现象，使等效塑性应变变小。

当侧压力系数k＝2.0时，隧道右侧受到的侧压力大于隧道上部受到的主压力，此时顶部与底部受压，隧道两侧拱脚受拉，隧道围岩塑性极值区位于隧道右侧拱脚处附近，等效塑性应变增大。

3.2 衬砌厚度对隧道围岩塑性区的影响

在正弦波形式作用下，取幅值为500 MPa、作用时长为0.05 s的加载条件。根据规范GB 50086—2015，选取衬砌厚度为 150 mm、160 mm、170 mm、185 mm及200 mm来研究衬砌厚度对隧道开挖过程中围岩稳定性的影响。

当衬砌厚度不同时，第26步开挖结束后的衬砌应力分布形式如图8所示。综上可知，随着衬砌的加厚，隧道开挖结束后应力会相对减小，隧道的稳定性增强。但随着衬砌厚度的增加，改善效果有限，考虑到实际工程的需要与成本问题，当衬砌厚度为150 mm时，既能增强围岩的稳定性，又能节约成本。

图8 不同衬砌厚度对隧道围岩塑性区的影响

4 结论

本文通过改变扰动作用形式、作用时间周期、应力幅值来模拟隧道开挖过程中受到的动力扰动，并通过改变侧压力系数及衬砌厚度对隧道围岩的稳定性进行分析，得出如下结论:

(1)不同扰动作用形式对隧道围岩稳定性影响较大，梯形波作用形式下对围岩稳定性造成的破坏最大，折线波作用形式下造成的破坏最小，正弦波作用形式下造成的破坏居中。同种扰动作用形式下，随着应力幅值的增加，对应的应力和位移随之增加，隧道围岩塑性区面积增大，隧道围岩稳定性越差；作用时间周期变化对围岩的稳定性影响不大。

(2)侧压力系数对隧道围岩稳定性影响较大。侧压力系数的变化会改变隧道洞周的应力状态，从而对塑性区的分布状况造成影响。在实际施工过程中，应考虑初始地应力的分布情况以及施工过程中机械扰动对隧道围岩稳定性的影响。

(3)衬砌厚度的增加会使隧道围岩稳定性增强，可根据实际工程需要进行经济最优化选择。