充填型岩溶管道致灾机理研究

王青松

(1.中铁二十局集团有限公司 陕西西安 710016；2.长安大学 陕西西安 710064；3.中国铁建高原隧道施工技术及装备研发中心 陕西西安 710016)

1 引言

突水突泥是岩溶隧道修建过程中最常见且极具危害性的一类灾害，其往往具有突发性，极易造成重大经济损失及人员伤亡[1－3]。岩溶隧道突水致灾构造通常包括:断层型、泥砂充填型溶洞、高压富水溶洞、暗河、裂隙、填充型岩溶管道等类型[4－6]。其中充填型岩溶管道往往规模较小，前期地质勘察难以发现，在复杂的地下岩溶水循环路径中，岩溶管道往往连接广泛的地下水补给网路和充足的补给水源，隧道施工中一旦揭露，极易造成严重的工程灾害和环境破坏。

当隧道开挖揭示填充型岩溶构造时，隧道是否发生突水与填充介质的性质和稳定性密切相关。由于填充介质的渗透性存在差异，其通常包括整体滑移和渗透失稳两种破坏类型。当充填介质结构致密、胶结程度高，整体性好，其往往具有良好阻水能力，且与岩溶管壁结合紧密，起到了“瓶塞”的作用。填充型岩溶构造一旦揭示容易在隧道施工中持续的爆破振动以及岩溶静水压力的综合作用下，填充物内部或岩溶管壁处发生剪切破坏，导致填充物大范围滑动失稳而最终发生突水突泥[7－8]。当充填介质结构疏松、孔隙率大时，水流会对充填介质进行浸泡和冲刷，充填介质颗粒不断被冲刷运移，管道内部的孔隙率越来越大，随着较大介质颗粒散失，充填管道最终贯通导致隧道发生突涌水[9－10]。因此充填管道型岩溶通常表现为“延滞性溃水”。

对于充填管道型岩溶，很多学者做了相关研究。李术才(2015)[11]利用条分法计算了充填型岩溶蓄水构造突水突泥的安全层厚度。CHU Vietthuc(2016)[12]采用理论分析结合数值模拟，分析了充填型岩溶管道的突水机理及演化过程。储汉东(2017)[13]利用极限平衡法建立充填体滑移失稳模型。黄震(2019)建立了充填型岩溶管道的力学传递模型，并推导出岩溶管道失稳判据及安全系数计算公式。本文针对充填体滑移失稳，忽略岩溶充填体的渗透水压力，建立了岩溶管道充填体临界安全厚度计算公式；针对充填体渗透失稳，建立了岩溶管道充填体渗透失稳力学模型；最后通过数值模拟揭示了充填型岩溶管道致灾呈“滞后性”的内在机制，以期为相关工程实践提供参考。

2 充填结构物滑移破坏

当充填介质结构致密、胶结程度高，整体性较好，渗透性较小时，具备优良的阻水能力，甚至可以将其视作隔水层，往往起到“瓶塞”作用。隧道开挖打破了原有平衡状态，为充填体提供了整体滑动的致灾条件，本文不考虑水的渗透力，建立充填体滑移失稳力学模型。

如图1所示，将模型简化为平面二维模型，溶管宽度为D，长度为L，溶管内为静储量岩溶水，水压均布于充填体顶面；填充介质为完整致密体，仅在溶管壁处产生滑移而失稳；充填型溶管揭穿时失去原有支护力，即q＝0。

图1 填充体滑移失稳力学模型

根据力的平衡，填充体的极限平衡方程为:

式中:F为充填体所受摩擦力；G、P和α分别为充填体所受重力、水压力及充填体倾角，则有:

式中:γ为充填体容重；D和L分别为充填体宽度和长度；Pw为上部均布水压。

充填体内部任一点的抗剪强度为:

由于破裂面为直立面[13]，所以:

式中:λ为侧压力系数。

则该充填体侧面受到摩擦力为:

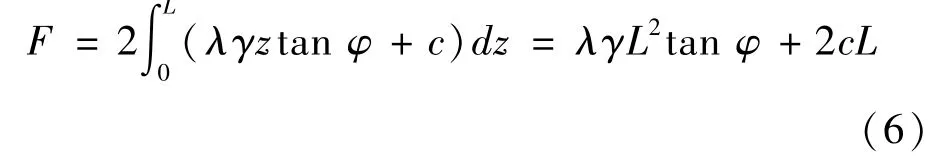
得到充填物滑移力学模型:

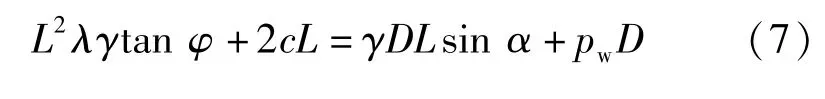
式(7)中等号左侧为抗滑力，右侧为致滑力。通过求解得到充填物滑移的临界长度:

对充填滑移体临界长度L0变化规律进行分析，假定充填体参数不变。

计算参数如表1所示，在研究滑移体临界长度L0与宽度D的关系时，假定其他三项不变，并以此类推，得到滑移体临界长度L0随宽度、倾角、侧压力系数及水压的变化规律，如图2～图5所示。

表1 滑移充填体计算参数

图2 临界长度随管道宽度变化规律

图3 临界长度随管道倾角变化规律

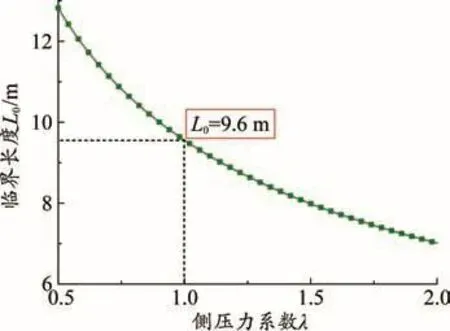
图4 临界长度随侧压力系数变化规律

图5 临界长度随水压变化规律

(1)充填滑移体临界长度L0随宽度D的增加而增大，但增长速率呈现减小趋势，当充填体宽度D在2.0 m以上时，临界长度L0随宽度D近似呈现线性增加关系。

(2)充填滑移体临界长度L0随倾角的增加而增大，增长速率呈现减小趋势，当充填体倾角小于45°时，充填滑移体临界长度随倾角α增加近似呈线性增长；倾角大于60°时，增长率明显降低；倾角在75°～90°，充填滑移体临界长度几乎保持不变。

(3)侧压力系数λ的增大意味着摩擦力的增大，因此充填滑移体临界长度随侧压力系数的增加而减小，但其减小的速率逐渐变小。例如侧压力系数从0.5增加到1.0时，临界长度L0从12.8 m减小为9.6 m，降低了约25%；而侧压力系数λ从1.0增加到1.5时，临界长度L0从9.6 m减小为8.0 m，只降低了约17%。

(4)充填滑移体临界长度随水压的增加而增大，当水压较小时增速较快，当水压较大时增速逐渐降低。例如水压pw从0.5 MPa增加到1.0 MPa时，临界长度L0从6.4 m增大为9.6 m，增加了50%；水压pw从1.0 MPa增加到1.5 MPa时，临界长度L0从9.6 m增大为12.0 m，增加了25%。

值得注意的是，实际施工中爆破等振动作用会对充填介质起到一定扰动作用，而且水的渗流会产生一定的渗透力，为了简化计算此处并没有考虑这些因素，因此建议在计算所得的临界安全长度L0的基础上乘以一定的安全系数η，即L＝ηL0，安全系数η亦可根据实际工程进行分析。

3 充填结构物渗透破坏

以圆形岩溶管道为例，将胶结紧致的充填介质视为一个整体，岩溶水的渗透力为体积力，并与渗流方向一致，当填充介质出现微小移动时，构建如图6所示力学模型[12]。

图6 圆形填充型管道渗流示意

管道中任一点受到的水压力为:

式中:为渗流产生的动水压力矢量；γ为渗流水的容重；为水力坡度矢量。

设溶管沿x方向水力梯度变为J，则dx微元内的填充介质所受渗流力为:

式中:J为水力坡度；n为填充介质孔隙率；w为圆形微管道直径。

充填介质发生移动时，会受到管壁阻力，并且管壁阻力和充填介质对管壁的拖曳力互为作用力和反作用力，其大小为:

根据微元体的受力平衡有:

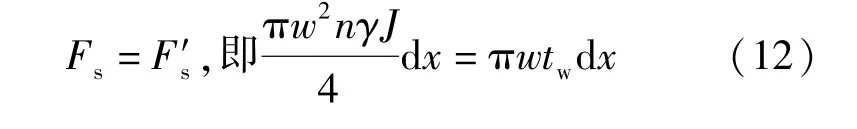
进一步得到:

当溶管内全为水体，没有固体颗粒填充介质时，即n＝1，则:

式中:ρw为水的密度。

当固体填充介质颗粒发生移动时，将岩溶水和颗粒共同运动简化为某种单相高密度流体，则其对管壁产生压力:

式中:ρm为混合流体密度；ΔH为渗流总水头和位置水体的水头差。

此时，管壁受到流体的拖曳力为:

由于混合流体的密度ρm大于单一水体的密度，因此相对于岩溶水而言，泥砂混合流体对管壁的拖曳力更大，因此其扩径作用也更为明显。

4 岩溶管道突水演化过程分析

采用数值模拟对管道型岩溶突水过程进行模拟。计算模型尺寸为(160×160×2)m。假定岩溶管道上方连接高压富水溶洞，水压为1 MPa。隧道埋深100 m，围岩孔隙率为0.2，渗透系数为1×10－10m/s；充填体孔隙率为0.3，渗透系数为1×10－8m/s，地层侧压力系数取1.0。数值模拟计算参数如表2所示，数值模拟计算结果如图7所示。

表2 数值模拟计算参数

图7 数值模拟渗流计算结果

由图7可知，初始最大孔隙水压力主要发生在岩溶管道的充填体处，隧道开挖以后充填体的孔隙水压力呈现先减小再增大的变化规律，这是因为隧道开挖以后形成临空面，加速了充填体内部孔隙水的流通；同时由于充填体结构致密，具有很好的阻水性，因此上部的岩溶水还未补充，随着时间的增加，上部水体通过渗流作用再次补充了充填体内部的孔隙水，并且水压持续增大，最终充填体发生滑移破坏，反映出管道型岩溶突水突泥呈现“延滞性”的特征。

5 结论

本文针对管道型岩溶致灾机理进行研究，主要取得以下结论:

(1)建立了岩溶管道两种失稳模型，包括充填滑移破坏和渗透失稳破坏，且推导了不考虑水体渗透力时充填滑移破坏类型的临界安全厚度计算公式。

(2)管道型岩溶充填滑移体临界长度随宽度的增加而增大，但增长速率呈现减小趋势；当充填体倾角小于45°时，充填滑移体临界长度随倾角近似线性增加，当倾角大于60°时，增长率明显降低；充填滑移体临界长度随侧压力系数的增加而减小，但其减小的速率逐渐变小；临界长度随水压的增加而增大，但增速逐渐降低。

(3)隧道开挖以后充填体的孔隙水压力呈现先减小再增大的变化规律，并且随着水压持续增大，充填体最终发生滑移破坏，反映了管道型岩溶突水突泥呈现“延滞性”的特征。