椭圆方程约束最优控制问题的深度计算
2022-01-19辛梦琦毕春加
辛梦琦,毕春加,杨 旻
(烟台大学数学与信息科学学院,山东 烟台 264005)
带偏微分方程(PDE)约束最优控制问题[1]主要研究目标泛函受偏微分方程约束的最优化求解,属于数学和工程领域一个重要且有意义的研究方向,在医学、物理学、金融学等领域有着非常重要的应用。传统求解带PDE约束最优控制问题的方法一般包含两个步骤:离散处理和优化算法设计。例如,高新[2]研究了交替方向乘子法、惯性交替方向乘子法和对称交替方向乘子法,这三种方法都是采用先离散后优化的思想。张倩[3]采用了浸入有限元和变分离散相结合的方法来离散模型。但是,采用传统计算方法往往面临收敛速度慢、难以处理复杂高维问题的困难。
近年来,深度神经网络在机器学习和人工智能领域受到广泛应用,其强大的非线性拟合能力使其能够解决极为复杂的实际问题。最近将深度神经网络用于求解微分方程(组)成为一大研究热点。例如,RAISSI等[4]提出了基于物理信息的神经网络(PINNs),将微分方程残差作为正则化项整合到损失函数中来求解PDE正反问题。该方法又进一步被应用于求解复杂的分数偏微分方程[5]以及几何偏微分方程[6]。
基于上述研究工作,本文拟将PINNs应用于求解受PDE约束的最优控制问题:
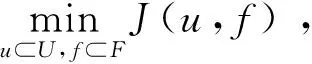
s.t.e(u,f)=0,
f∈Fab⊂F。
(1)
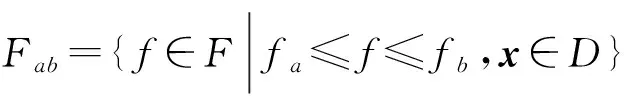
与普通的偏微分方程相比,由于最优控制问题(1)中既有PDE又有目标泛函,因此需要建立一个统一的优化目标以供神经网络进行学习。其次,针对控制变量和状态变量同时存在的情形,需要设计恰当的神经网络以协调两者之间的内在联系。
与传统的数值方法相比,基于深度学习的方法具有很好的泛化性,所建立的模型能用于一类相似的最优控制问题求解,并且由于方法本身基于物理模型,无需考虑网格离散的问题,因此易于推广到复杂区域和高维情形。
1 深度计算方法
1.1 神经网络


(2)
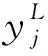
… …
… …
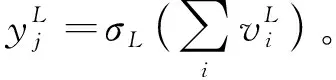
(3)
当使用深度神经网络求解PDE问题时,神经网络的输入为区域中任意样本点的坐标信息,而神经网络的输出则为对应解的近似估计,即整个神经网络相当于解的一个非线性拟合函数。针对不同的问题,人们往往需要建立恰当的优化目标,从而让神经网络在训练过程中确定最优的网络权重和偏置系数。不同的网络结构以及不同的训练方法,往往会对求解效率和精度产生较大的影响。
1.2 椭圆方程约束最优控制及深度求解
考虑如下稳态椭圆方程约束最优控制问题:

(4)
其中,ud,f0为已知量,r为常数,A,b,c为关于x的函数。为了能够使用神经网络进行计算,将针对式(4)构建恰当的优化目标。

本文将考虑二维的情形,因此,在给定采样点后,原优化目标可近似为
其中n为样本数。进一步地,把椭圆方程中的边界和控制变量约束作为“软”惩罚整合后可得如下统一的优化目标:
(5)

注意到式(5)中的第四项,我们给出了一个特殊的平方损失函数,从而巧妙地把控制变量约束转化成目标函数的一部分。当控制变量f不受约束时,可令β=0,当控制变量f带约束时,β≠0。
2 数值实验
实验的运行环境为:Windows 10系统,CPU i7-8700,Tensorflow 2.2,实验中神经网络的激活函数是双曲正切函数(Tanh)。另外,神经网络使用L-BFGS-B(拟牛顿算法)[9]来迭代求解损失函数。
考虑两种情况:一是控制变量无约束,即Fab=F;二是控制变量带约束,即Fab={f∈F|fa≤f≤fb,x∈D}。其中D=[0,1]×[0,1]⊂R2,r=1,A=1,b=0,c=0,真解均取为ud=sin(πx1)sin(πx2),f0=2π2sin(πx1)sin(πx2)。
训练学习过程中,在区域D和边界∂D上随机采样n个点,默认n=100×100,默认神经网络包含3个隐藏层,其神经元个数为[32,16,32]。而测试阶段,在计算区域另外均匀采样40 000个点,在这些点上与真解进行比较以检验方法的精度。
2.1 控制变量无约束
首先考虑控制变量无约束的情况,此时式(5)的超参数β=0,相应损失函数为
(6)
2.1.1 不同超参数下误差分析 由于超参数α是人为设定的,不同的α会对实验结果有一定的影响。为此本文首先进行四组实验,分别取α=1,2,3,4,相应的误差热力分布图如图2,3所示。

图2 函数u的预测精度Fig.2 The prediction accuracy of u

图3 函数f的预测精度Fig.3 The prediction accuracy of f
从热力分布图2,3可以看出,在控制变量f不带约束时,本文给出的深度学习方法能够很好地计算出原问题的近似解。不同的超参数α的取值对计算结果具有一定的影响,当α=2时,精度表现是最好的。
为了进一步测试超参数α对实验结果的影响,同时检测超参数α的选取是否会随网络结构的变化有所不同,本文又进行了多组实验,表1显示了在不同网络结构以及超参数α下,解的均方误差情况。从表1中可以看到,尽管改变了网络结构以及超参数α,本文使用的方法依然有效,同时也可以看到,在不同的网络结构下,超参数选定为2时,均有较好的表现。
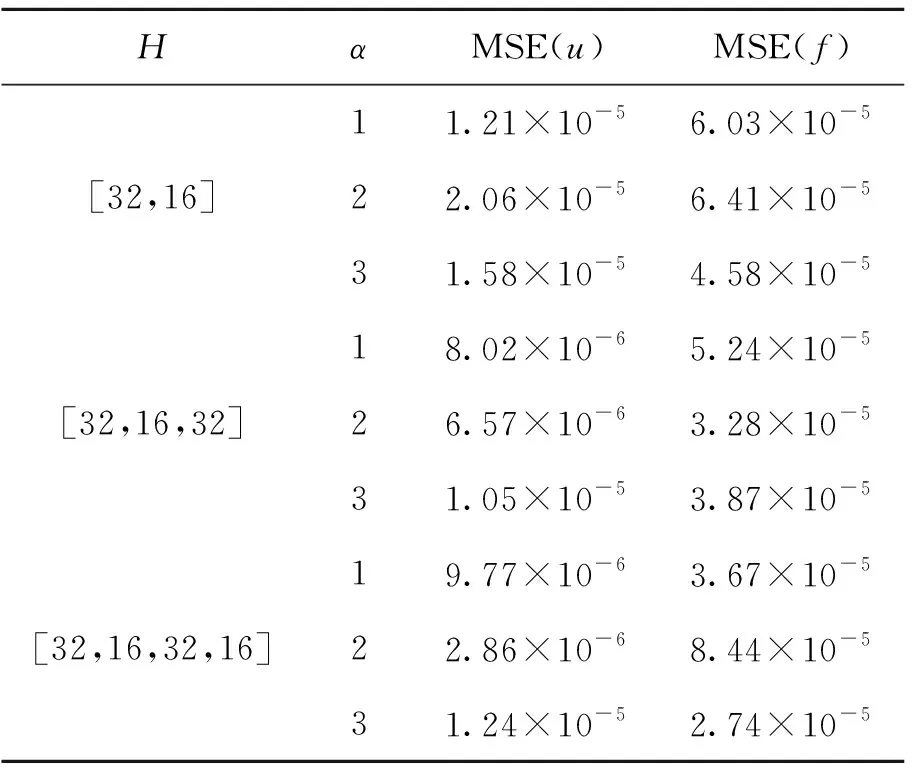
表1 函数u和f的均方误差Tab.1 The mean square error of u and f
2.1.2 神经网络结构的影响 通常来说,神经网络的深度和宽度对学习效果会有很大的影响,随着网络深度和宽度的增加,人工神经网络的非线性拟合能力会有很大的提高。本小节考查网络的深度对椭圆方程约束的最优控制问题预测精度的影响。
实验中固定超参数α=2,改变隐藏层的网络结构H,其他保持不变。表2显示了在不同神经网络的深度下,整个域中解的均方误差的情况。由表2可以观察到,通过增加网络的深度,该方法在求解椭圆方程约束的最优控制问题上的预测精度有了不同程度的提高。
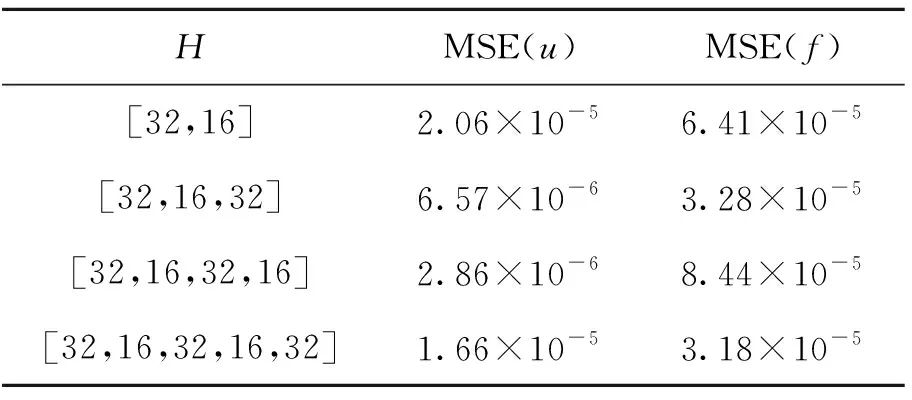
表2 不同神经网络结构下函数u和f的均方误差Tab.2 The mean square error of u and f with different neural networks' structure
2.1.3 样本数的影响 在本节中,我们考察采样点数量对解的影响。仍然固定α=2,表3显示了在不同采样点数量的情况下,解的均方误差。从表3中可以看到,随着采样点数量的增加,预测精度有了明显的提高。

表3 不同样本数下函数u和f的均方误差Tab.3 The mean square error of u and f with different number of samples
2.1.4 不同训练方法的影响 不同的训练方法往往会对实验结果产生较大的影响,因此,本节将把L-BFGS-B与常见的SLSQP(最小二乘法)[10]进行比较,同样的,我们进行了多组实验,实验结果如表4所示。可以看到,使用不同的训练方法,对实验结果的精度会有一定的影响,并且对于以上两种方法而言,使用L-BFGS-B更有效。

表4 不同训练方法下函数u和f的均方误差Tab.4 The mean square error of u and f with different training methods
2.2 控制变量带约束
接下来考虑控制变量带约束的情况,设f的下界fa=0,上界fb=20。此时式(5)中β≠0,神经网络的损失函数就是式(5)本身。同超参数α一样,β的选择对实验结果也有一定的影响。为了探究此方法在控制变量带约束时的预测准确性以及研究超参数β对预测精度的影响,我们依然进行了四组实验,这里保持α=2,分别取β=0.1,0.5,1,2,实验结果如图4,5所示。
从图4和图5的热力分布图中可以观察到,对于控制变量f带约束的情况下,采用深度学习方法依然有效。同时,对于不同的超参数β误差会有所不同,但总体表现是比较稳定的。

图4 函数u的预测精度Fig.4 The prediction accuracy of u
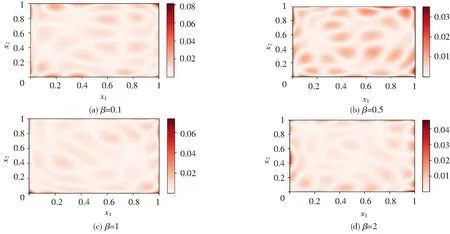
图5 函数f的预测精度Fig.5 The prediction accuracy of f
3 结 论
本文提出了一种基于深度学习求解椭圆方程约束最优控制问题的方法,实验结果表明所提出的深度计算方法无论是精度还是鲁棒性都有很好的表现。对于非稳态PDE约束以及边界带控制变量的最优控制问题将是下一步研究的方向。
