仿蝠鲼航行器游动规律智能控制与优化方法

魏旭飞，刘洲阳，魏先利

（航天科工集团第三研究院水下装备总体部，北京 100074）

0 引言

海洋中的鱼类等生物经历了亿万年的演化，在水下运动和环境适应能力上展现出优越特性，研究人员“道法自然”，开展了大量仿生水下航行器的研究[1-3]。然而，受限于传感器、材料、结构和控制等技术，仿生水下航行器相较于真实鱼类在许多指标上还有较大差距。以推进效率为例，依靠尾和鳍的协调运动，普通鱼类的推进效率可达80%，鲹科鱼类则超过90%，而普通螺旋桨推进器的平均效率仅为 40%～50%[4]。因此，如何提高游动性能已经成为仿生水下航行器领域一个重要的科学问题。

游动性能的提升涉及水动力构形、结构机构、驱动方式、运动控制等多学科的优化，是个非常复杂的耦合问题。Anderson设计了升沉和俯仰2个自由度的二维平板摆动实验，通过测量尾鳍输入和输出的功率来计算推进效率，证明了仿生机器鱼推进效率优于传统机械方式[5]。哈工程的苏玉民团队从水动力性能出发，通过计算流体力学仿真发现调整弦向变形相位角可以使尾鳍节省能量[6]。中科院自动化所喻俊志团队从驱动装置优化的角度出发，设计曲柄滑块装置，避免了电机因不断加速和减速而造成的能量损失，从而提升了性能[7]。北航梁建宏团队通过水动力学定性观察和定量测量实验发现游动能耗会随着摆动频率和相对波长的增大而增大[8]。国防科大王光明团队通过样机试验研究了波动鳍条结构、鳍面材料、摆动频率和波形数目对波动鳍推进效果的影响，发现摆动频率和幅值对推进性能影响最大[9]。

可以发现，目前仿生游动性能的研究主要采用计算流体力学和样机试验方法，通过人为控制各运动参数来探究游动性能的影响因素，获得的往往是一套固化的游动参数。然而，真实鱼类的游动规律会随着水下环境的变化而变化，若采用固化的游动规律，仿生航行器的表现显然是差强人意的。为了解决这一问题，本文将采用深度强化学习（deep reinforcement learning，DRL）方法，在初始游动规律的基础上进一步挖掘仿生航行器游动性能的提升空间，通过仿生航行器的自我试错，在游动参数空间中学习高效的游动策略。

1 深度强化学习训练环境

训练环境主要包括航行器运动特性的模拟，状态空间、动作空间与回报函数的设计，并承担着数据归一化、游动性能评价、回报函数计算等作用。

1.1 仿蝠鲼运动模型

仿蝠鲼航行器通过柔性胸鳍摆动提供矢量推力实现机动航行。胸鳍运动可简化为沿展向的周期性摆动运动和沿弦向的周期性扭转运动，其数学描述如下：

式中：下标flap代表摆动；θflap(t)为t时刻的摆动角；Aflap为胸鳍最大摆幅；fflap为胸鳍摆动频率；φ0flap为胸鳍摆动初始时刻相位，Bflap为胸鳍摆动角偏置；下标twist代表扭转；θtwist(t)为t时刻的扭转角；Atwist为胸鳍最大扭幅；ftwist为胸鳍扭转频率；φ0twist为胸鳍扭转初始时刻相位；Btwist为胸鳍扭转角偏置；Δφ是胸鳍扭转角初始相位与摆动角初始相位的差值，简称扭摆相位差。

1.2 状态量和动作量设计

仿蝠鲼航行器的游动过程可用马尔科夫决策过程建模描述。考虑仿蝠鲼航行器智能体与环境的交互轨迹：

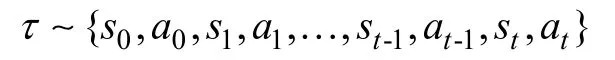
式中：st表示t时刻智能体的状态；at表示t时刻智能体执行的动作。对于深度强化学习而言，选取何种状态量作为智能体的观测进行训练直接影响算法的收敛能力，需要精心设计。为充分描述航行器前向游动状态，本文选取5维向量st=[dvx,vx,vy,ϑ,wz]作为状态量，包括期望前向速度与当前前向速度的差dvx、前向速度vx、航行器y轴速度vy、俯仰角ϑ和俯仰角速度wz。其中各参数的取值范围及含义详见表1所示。

表1 智能体观测状态量Tab.1 Observation variables of the agent

考虑到设计目标是提升航行器直航过程中的游动性能，为了降低问题的维度，减少不必要的试错成本，本文选用左右胸鳍对称运动的方式。此外，为降低仿蝠鲼航行器往复的俯仰运动对游动平稳性的影响，设计PD控制器以期望俯仰角为零进行俯仰控制。综上，本文选取at=[Aflap,Atwist,Δφ]作为智能体的动作量，包括胸鳍摆幅Aflap，胸鳍扭幅Atwist和扭摆相位差Δφ，各动作量的取值范围和含义如表2所示。

表2 环境模型动作量Tab.2 Action variables of environment model

此外，胸鳍的运动频率设置为fflap=ftwist=0.5 Hz，摆动角偏置Bflap和扭转角偏置Btwist设置为 0°。为降低数据的方差，提高深度神经网络收敛速度，状态量和动作量在送入深度神经网络前进行归一化处理，将其取值归一化到[-1,1]范围内。

1.3 回报函数设计

回报函数设计是深度强化学习研究中的重要环节，需要根据任务进行人工设计和调优。本文选用如下的直航游动性能评价方式：

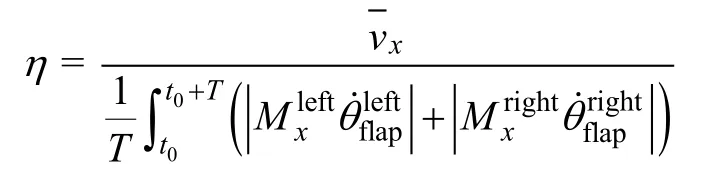
基于上述评价方式，回报函数设计如下：

式中：W为航行器在一个周期内航行所耗费的功；reward0为回报函数基准；0.35是期望速度，m/s。

2 基于DDPG的仿蝠鲼航行器游动性能优化控制

DDPG算法非常适合解决连续动作空间问题[10]，在此基础上，本文利用经验回放池（replay experience buffer）和预热轮（warm up）方式提高样本利用率，改善DDPG的学习能力。

2.1 算法结构

DDPG由4个网络组成，分别是：Actor当前网络、Actor目标网络、Critic当前网络、Critic目标网络。为了稳定学习过程，采用软更新机制更新网络参数，即

为了增加算法的探索性，DDPG的动作A会增加噪声N：

Critic当前网络的损失函数是：

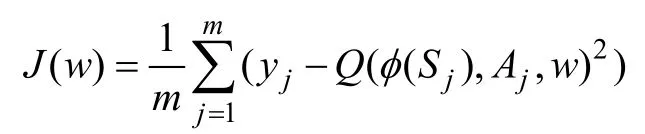
Actor当前网络的损失函数是：

2.2 训练样本

经验回放池replay buffer的总存储量1 000 000，在warm up至其中有256个样本后开始训练。每批次在 replay buffer中随机选取 128个样本进行学习，取训练总步数为500 000。

2.3 控制模型设计

控制算法模型为多层感知机。Actor网络采用节点数分别为64和32的两层全连接隐层，激活函数使用Relu。输出层选用全连接层，维度为3，激活函数选用 tanh，保证 Actor网络的输出在-1～1之间。Actor网络使用Adam优化器进行参数优化，学习率0.001。

Critic网络采用节点数分别为64和32的两层全连接隐层，激活函数使用Relu。输出层为状态-动作值Q，维度为1。Critic网络使用Adam优化器进行参数优化，学习率0.001。

同经典 DDPG算法一致，本文使用目标网络增强神经网络收敛的稳定性，取更新系数τ= 0.001。在控制策略探索方面，为保证算法具有一定的探索性，在归一化的动作量上添加期望为 0，方差为ε= 0.1的高斯噪声。

2.4 训练周期

仿蝠鲼航行器选取 0.5 Hz的胸鳍运动频率，胸鳍控制信号 1 s更新一次，尾鳍控制信号 0.1 s更新一次。为了更加准确地评估胸鳍运动方式对游动性能的影响，强化学习的步长与胸鳍运动周期保持一致。航行器运动5个周期构成一次训练轮次。

2.5 终止条件设计

每轮训练的终止条件是完成全程航行或失稳。

完成全程航行主要根据该轮次的终止时间判断，若终止时间等于该轮次的设计航行总时间则判定航行器成功完成全程航行。

失稳判定主要依据姿态角和速度，标准为

当一轮训练终止而当前训练总步数未达设计训练总步数时，重置环境，开始新一轮训练。

3 训练及仿真试验结果

3.1 训练结果分析

训练持续2 000步左右时模型收敛，继续训练到45 000步提前终止训练，图1为训练过程中回报函数值随训练步数变化曲线。

图1 训练过程中回报函数值变化情况Fig.1 Variation of train reward during training

图2为训练过程中每隔100步进行测试的回报函数曲线，可以看出神经网络模型的收敛较为稳定，即使因为随机样本导致学习偶尔进入局部最优也能很快恢复到较好的水平。

图2 训练过程中测试时的回报函数值变化情况Fig.2 Variation of evaluate reward during training

3.2 控制结果分析

为评估神经网络控制模型的控制效果，首先考察基准控制策略的控制效果。以摆幅30°，扭幅30°，相位差90°这一固化游动控制策略作为基准进行控制仿真。仿真中取初速度0.35 m/s，仿真40 s，过程中状态量变化情况如图3所示。从图中可以看出，航行器平均速度约为0.32 m/s，俯仰角在±30°以内。

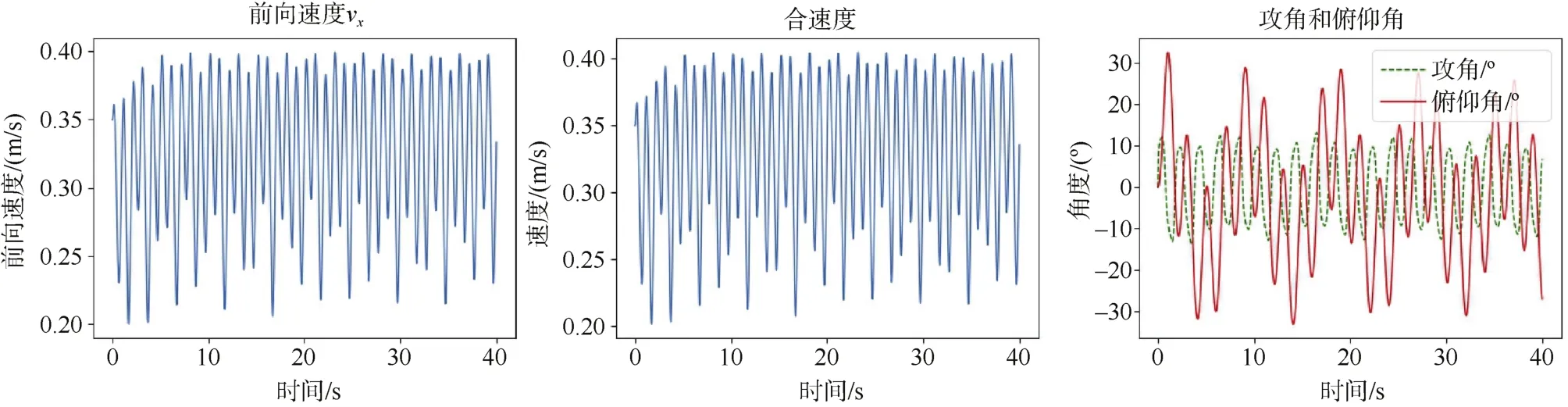
图3 基准控制策略下系统状态变化情况Fig.3 System state variation during baseline swimming strategy

图4展示了胸鳍摆动和扭转运动的实际变化情况，其中上方为实时控制指令，下方为经过舵机模型后的实际执行指令，相比实时控制指令存在一个较小的延迟。可以看出，航行器胸鳍摆动和扭转均以正弦形式运动，运动曲线平滑连续。

图4 基准控制策略控制摆幅和扭幅实际值Fig.4 Variation of the amplitude of flap and the amplitude of twist during baseline swimming strategy

经统计，在基准游动控制策略下，航行器平均速度0.325 7 m/s，游动能效为0.052 7 m/J。

接下来验证基于DRL的控制模型。令航行器以初速度0.35 m/s开始航行40 s，完成任务后查看航行状态，统计平均游速和游动能效值。

图5展示了收敛后的神经网络模型控制状态变化。从图中可以看出，航行器平均速度在0.4 m/s附近，俯仰角保持在±40°以内。3个执行机构的可控维度均参与了控制，摆幅在12°～30°之间变化，扭幅变化不大，基本维持在 30°附近，相位差在125°～180°之间变化。

图5 神经网络模型系统状态变化情况及动作量）Fig.5 The variation of system state and action during NN-based swimming strategy

图6展示了胸鳍摆动和扭转运动的实际变化情况，其中上方为实时控制指令，下方为经过舵机模型后的实际执行指令。可以看出，航行器胸鳍摆动和扭转均以正弦形式运动，运动曲线在指令切换时存在较小的抖动但仍处于可用状态。

图6 神经网络模型控制摆幅和扭幅实际值Fig.6 The variation of flap amplitude（left）and twist amplitude（right）during NN-based swimming strategy

经统计，在基于DDPG的游动控制策略下，航行器平均速度0.372 8 m/s，游动能效为0.065 6 m/J。相比基准游动控制策略，航行速度提升0.047 1 m/s（14.46%），游动能效提升0.012 9 m/J（24.48%）。

4 结束语

本文从控制策略优化的角度出发，以仿蝠鲼航行器为研究对象，使用基于DDPG的DRL方法对直航游动规律进行优化。训练完成后与固化的游动策略进行了比较，在 40 s的游动时间内，优化后的游动策略在航行速度上相比基准游动控制策略提升了14.46%，在游动能效上降低了24.48%，在降低能量消耗的同时获取了更快的前向游速，从而实现了游动性能的提升。该方法同样适用于其他仿生推进方式的水下航行器游动规律优化设计。