基于半圆柱形峡谷对SH波散射的经典模型退化验证分析＊

屈恩相，齐 辉，郭 晶，吕 春，王 丽，王洪志，郭国梁

（1.齐齐哈尔大学建筑与土木工程学院，黑龙江 齐齐哈尔161006；2.哈尔滨工程大学航天与建筑工程学院，黑龙江 哈尔滨150001）

弹性波动理论研究中的对SH波的散射问题一直是研究的热点，在近几十年的科研人员的不懈努力下取得丰富的成果[1-11]。这将进一步推动地震工程、岩土工程等领域的向前发展。研究分析的方法包括解析法和数值法。解析法包括波函数展开法、复变函数法等，数值法包括有限元法、边界元法等。那么在二维弹性波入射含凹陷地形散射问题时，又可以分为稳态和瞬态问题。两者的区别可以简单地理解为所分析的问题是否与时间量有关。稳态是忽略时间项的影响，而瞬态则是可以研究某一时刻的状态。根据介质属性可以分为各向同性和各向异性。两者的区别在于物理性质是否与方向相关。一些学者[3-11]在含半圆形凹陷地形的经典模型基础上，研究了单个或多个半圆形凹陷地形的稳态与瞬态问题、材料属性为各向同性与各向异性等不同方面。本文将选取部分文献的部分内容用以说明模型退化方法的有效性和价值性。

1 半圆柱形峡谷经典模型

文献[1]研究的半圆柱形峡谷的二维平面模型如图1所示。可以描述成一个半空间（y＞0），从这个半空间中移出了半个半径为a的圆柱体而形成一个峡谷。TRIFUNAC在文章中作出一些假设，半空间是弹性的、各向同性和均匀的。它的材料特性由硬度μ、剪切波速度β和入射波的入射角度γ。该理论模型建立两种坐标系，第一种直角坐标系是以半圆形的圆心为中心，x轴指向右侧为正向，y轴指向下侧为正向。另一种是极坐标系是以径向距离r和角度θ来建立。该文研究了半圆柱形峡谷对平面SH波的散射和衍射问题，定性地解释1971-02-09加利福尼亚圣费尔南多地震期间在帕科马峡谷边缘附近记录了帕科马大坝加速度。所研究的模型可以精确地以封闭形式求解，采用解析法中波函数展开法对经典模型进行研究用以检验数值法中有限差分或有限元法近似方法的准确性。

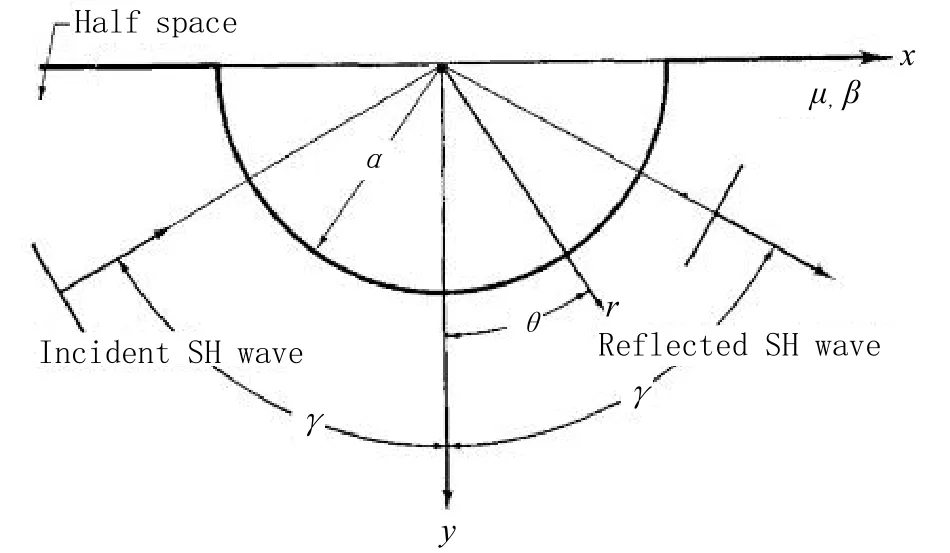
图1 半空间半圆柱峡谷的理论模型

2 经典模型部分算例分析

本文提取TRIFUNAC文章中的部分算例来进行阐述研究，图2中的3个图是其他参考文献模型退化的主要依据。其中λ=βT是入射波的波长，T=2π/ω。定义另一个无量纲参数η=2a/λ，其中η是峡谷a的半径与入射波半波长的比值，但也可以认为是无量纲频率，因为η=ωa/πβ或者无量纲波数η=ka/π。图中横坐标表示无量纲参数x/a，其中x/a=0对应峡谷中心，x/a=±1对应峡谷边缘。纵坐标表示入射平面SH波的表面位移振幅。图中分别讨论了η=0.25、η=0.75、η=1.25对应的不同SH波的入射角γ=0°、γ=30°、γ=60°、γ=90°的位移幅值关系，从而揭示一般规律性。从文献[1]中的部分算例可知，η=0.25时，γ从0°增大90°，不难看出x/a＜﹣1时，表面位移变化复杂振幅增加，x/a＞﹣1时，振幅减小并趋于平缓。表面位移由于峡谷的存在，对SH波产生散射和绕射而影响的。当入射角γ接近90°时，x/a=﹣1处峡谷左边缘起着阻挡作用，相当一部分能量返回来时的方向。η=0.75时，γ为0°，图形基本以x/a=0呈现左右对称。其他角度入射，位移幅值震荡变得更为复杂。η=1.25时震荡规律呈现无序型，但是基本能够看出x/a接近﹣1时，位移幅值达到最大值，然后出现震荡衰减。

图2 文献[1]中位移幅值随无量纲频率η的变化

3 模型退化分析

文献[3]的作者对各向同性、均匀线弹性介质的任意形凹陷地形对SH波的散射问题进行研究，用保角映射函数将任意形状凹陷半平面映射在一个完整的半平面上。通过构造入射波、反射波、散射波的波场表达式，写出二维凹陷地形总波场。将其代入满足边界应力为零的条件中，用Hermite函数展开，列出矩阵方程。截取有限项使得方程解收敛。得到的最后模型算例结果与经典模型文献[1]一致，说明复变函数法和保角映射方法应用到该理论模型中具有正确性。在文献[3]的基础上，文献[4]研究到各向异性介质中来进一步推广该方法的适用性。文献[3]与[4]的区别在于应力分量发生变化，由胡克定律可知各向同性均质弹性介质，应力分量的关系是其中μ为介质的弹性常数。各向异性均质弹性介质应力分量的关其中C55、C45、C44为介质的弹性常数。文献[4]中相关波函数的构造及公式推导也将发生变化。文献[4]中进行模型退化，这里令C45/C55=0，C44/C55=1，于是将各向异性弹性介质转为各向同性弹性介质。

在模型算例中可以发现，退化后的算例分析与文献[1]一致，这又进一步地推动了研究课题向前发展。将模型退化到经典理论模型中更说明了验证方法起到关键作用。文献[10]分析了半圆形凹陷地形内部含有裂纹的情况，该模型的提出对研究采油打井、开发煤矿、抗震抗爆等方面提供坚实的理论基础。该问题的提出是基于经典理论模型基础上而建立的，同样需要进行模型退化来证实理论推导、波函数的构造及边界条件的分析是否正确。文献[10]采用无量纲化分析。取凹陷的半径为1，裂纹的长度为0，这就是将所分析的问题退化为只有凹陷作用而无裂纹的情况。同样分析了入射角为0°、30°、60°和90°的情况。研究不同入射波数η为0.25、0.75、1.25的情况下，地表位移幅值的变化情况。得到的结果与文献[1]一致，说明该研究方法的有效性。

基于正确的前提下，又进一步地研究了直线裂纹的长度、地表与裂纹的中点距离以及选用几个不同波数和几个不同的入射角度对地表位移的影响；得出裂纹的存在而对地表位移产生了阻挡作用，进而使得凹陷区域震动减弱，而地表其余区域震动得到加强等有价值性结论。

文献[3][4][10]中位移幅值随无量纲频率η的变化如图3所示。

图3 文献[3][4][10]中位移幅值随无量纲频率η的变化

4 结语

在研究弹性波的衍射与动应力集中问题时，模型退化将成为一种有效的验证方法。基于模型退化后的正确性，不难看出可以将研究课题进一步拓展。不仅仅可以从凹陷存在的类别出发，还可以从缺陷存在的形式考虑。比如说增加凸起地形、孔洞、夹杂、衬砌或者是相互间若干种组合作用，还可以从材料的属性出发比如说各向同性、各向异性、均匀的、非均匀等进行延伸来分析其对SH波的散射影响。总之，这些被考虑问题的存在会增加研究问题的复杂性，也更能去解决一些实际问题。但是在此前提的基础上，需要验证其正确性。那么就需要对模型进行退化分析去验证所讨论问题。对于验证方面，也可以用不同研究学者所采用不同的处理方法进行相互验证。比如解析法与数值法讨论相同问题进行对比验证。科学的验证方法研究需要每位科研人员不断努力创新，以理论为基础解决更多有价值性工程背景的问题。