粒子量子态具有逻辑悖论属性的分析

高明*

（哈尔滨电气集团有限公司总部，黑龙江 哈尔滨 150028）

二十世纪量子力学的建立， 彻底改变了人类对物质世界的本质认识，实现了人类信息技术飞跃式发展，是人类认识世界和拓展世界的一个里程碑。然而由于量子态相对于经典态的特殊性，以传统的方式来分析、解释量子态始终存在着难以解释的矛盾，数学演绎多于对物理过程的分析。因此，量子理论自诞生之日起，以哥本哈根学派为核心建立起来的量子理论基本假设和解释始终受到一定的质疑，至今在科学界没有形成共识，本文以新的角度对粒子量子态的基本特性进行分析，给出了物理性的统一解释。本文从粒子量子态的时空属性分析入手，提出粒子量子态与经典态在时空属性方面存在的本质差异，运用叠加原理对粒子量子态的有关特性进行分析，得出了粒子量子态的相关属性具有辩证逻辑属性的结论。

1 粒子量子态的时空属性和关系分析

1.1 粒子的量子态的时空属性分析

从大量的实验结果我们观察到，粒子的量子态（以下文中没有特殊说明的量子态均指粒子的量子态）是一组量子态叠加而成的量子态波包，单一观测（非统计性观测）其变化的一个主要特征就是过程具有瞬时性。这和经典态的变化过程有着本质的区别，经典态的任何变化过程都有一个对应时间连续累积过程，而量子态则有瞬间不连续跳跃过程。因此，二者在时间性质上表现出的这种差异性是量子态和经典态的主要区别。因此，应该从时间属性特征出发，分析这种差异性的原因。

根据直观经验，具有时间属性的态有以下主要特征：

对于一个具有时间属性的态，对其进行观测，每一时刻都对应唯一确定的态（这个唯一确定态的物理特征是，在相同的观测条件下，观测结果保持唯一不变，即具有本征性，简单理解就是态有确定性），不会同一时刻对应不确定的态（这个不确定态的物理特征是，在相同的观测条件下，观测结果并不具有唯一不变性，即具有非本征性，简单理解就是态只有可能性而无确定性）。这正是时间可以标的这种态的原因所在，如果同一时刻对应的态具有不确定性，即非本征性，那么时间就无法标的这个态，这个态就不具有时间属性。对量子态进行有效观测，其每一时刻的态具有不确定的偶然性，根据上述直观经验，量子态不具有时间属性。下面运用狭义相对论来进一步证明这一结论。

假设粒子量子态波包（以下文中所提量子态波包是指粒子处于量子态未塌缩的情况）ψ 处于静止的K 惯性系，观测者处于运动速度为υ 沿一维x 方向运动的K′惯性系中（其中υ 并不一定需要高速，只要K′系与K 系存在速度差异即可）。在波包ψ 上取两点x1和x2（比如粒子量子态波包经过双缝，在左缝和右缝处各取一点）假定在量子态波包ψ 上的量子态有时间属性，ψ 塌缩时（比如在双缝处测量塌缩），x1和x2两处量子态塌缩消失的时刻分别是t1和t2，对应K′惯性系中坐标分别是x′1和x′2，对应两处量子态塌缩消失的时刻分别是t′1和t′2按照洛伦兹变换K′惯性系中x′1和x′2两处量子态塌缩的时间差为[1]：

由于A 处于静止的K 惯性系塌缩过程是瞬间的（后文分析原因），所以t1=t2，则有

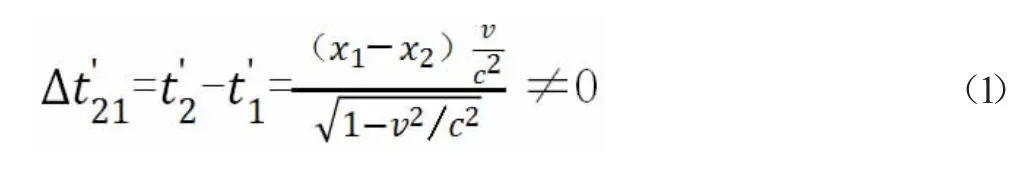
即只要速度υ 不为零，从K′ 惯性系观测波包A 的塌缩过程就不是瞬间的。但是实际情况是，由于粒子量子态波包A 在静止的K 惯性系的整体塌缩时间过程△t=0，同样根据狭义相对论在K′惯性系中观测到的整体塌缩时间过程为[2]

由(2)式可以得出x′1和x′2两处量子态塌缩时间差∆t′21=0的结论，(1)式的结果与此实际结果矛盾（这种矛盾的本质是出现了异地同时性），因此，前面在量子态波包A 上的量子态有时间属性的假定是不成立的，由此得出结论，量子态是不具有时间属性的。量子态无时间属性，由量子态线性叠加成的量子态波包也就不具有时间属性。但量子态波包在时空中确是一种客观存在，且时空属性构成一个完备的物理表象体系，因此，量子态波包只能是空间属性的存在，在量子态波包上，空间属性脱离了时间属性。由于量子态波包不具有时间属性，所以它的各种量子态之间就不具有时间顺序的因果关系（局域性），而具有空间整体的相关关系（非局域性）。由于整体相关关系，且没有时间属性，所以，量子态跃迁具有瞬时性才成为可能。粒子量子态只有纯三维空间属性，没有时间属性，而经典粒子具有四维时空属性，比量子态粒子多了一个时间维度，时间维度体现确定性，属于约束维度，因此，纯三维空间的量子态粒子自由度高于四维时空经典粒子自由度，所以，从经典的角度难于理解粒子量子态。但需要说明的是，波函数是有时间属性的，这是由于波函数是建立在粒子的波粒二象性转换基础之上的，它反映的是对量子态波包统计测量（非一次性测量）塌缩到测量仪器上的经典粒子的概率规律性结果表象，这个统计测量结果是经典统计本征的，是有时间属性的。但波函数不能反映单一量子态的具体物理属性和突变过程，而是对应反映量子态系综统计测量塌缩成经典态概率结果的数学有效表达，可以表现为复数形式，具有复空间意义。波函数表象可以描述量子态粒子，但不能描述塌缩后的经典粒子，这是因为在波包内的某一点测量，波函数既可能不塌缩，也可能塌缩，不塌缩可以有一个波函数描述，塌缩了就不能用波函数来描述了，否则在相同的初始状态、相同的环境和相同的测量作用方式下，同一粒子会有两个波函数描述，这与粒子波函数唯一性相矛盾。把经典态依据以往理论经验统一纳入量子波函数描述范围是造成量子力学内部诸多争议的主要原因所在。这也说明经典粒子不具有波函数所描述的概率性质，是局域的，在环境确定的条件下，状态具有唯一确定性。同前理，如果粒子量子态在同一的初始状态和同一的测量作用方式下既可能塌缩，也可能塌缩，如果塌缩过程中存在过程演变的波函数，不塌缩还对应一个波函数，则波函数在相同的条件下不具有唯一性，所以，粒子量子态塌缩成经典粒子的过程，波函数不是一个渐进演变的过程，而是一个瞬间塌缩的过程，且塌缩结果不具有波函数性质。正因为粒子量子态波包塌缩具有瞬时性，才会产生EPR 佯谬传态的瞬时性现象。

1.2 量子态叠加原理的分析及应用

量子力学一个基本原理就是态叠加原理。这一原理可以表述为：对一个量子系统ψ，在相同的条件下进行（一次性）观测，其观测结果既可能是A 也可能是A，系统状态表象具有不确定性，即系统相对于观测方式状态具有非本征性，那么系统ψ 在量子可能性层面可以表示为如下态矢量叠加关系（类比于波函数，但叠加关系并不仅限于波函数[3]）：

因为是定性分析态的表现形式，为简洁起见，略去态的概率和本征值相关系数。态矢量叠加表达式（3）是系统ψ 在量子层面对两种可能性（非确定性）态的数学有效表达，类比于波函数（具有复数形式），具有虚像意义；态矢量ψ 与经典确定环境发生关系的表象即等同于经典环境对其进行了观察（即与经典环境发生了物理关系，与人是否参与观察无关），同时，态矢量ψ被观测具有不确定的非本征性（既可能是A，也可能是A），因此，对其作用了具有统计性的观察算符（记作M˄）的结果才是态矢量相对于经典环境的现实的而且是确定的表达（类比于波函数加观察算符M˄，其结果为共轭波函数的内积，即波函数的模平方，从而才具有实数形式和概率实在意义），才具有实像物理意义。因此，量子系统ψ 在现实经典确定层面的表象结果必须对其作用一个观测算符M˄，其展开结果如下[4]：

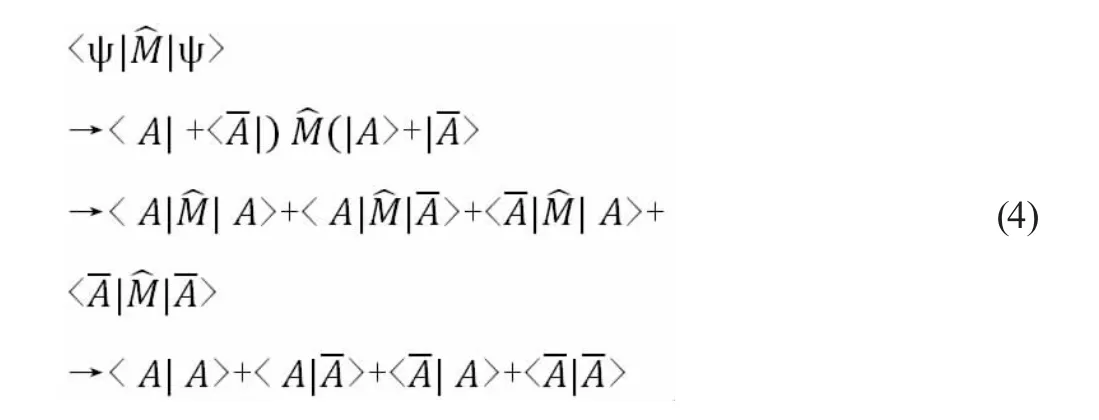
由(3)式变换为(4)式，就完成了由可能性（不确定性）结果向确定性的结果的转换，这是具有通用性意义的变换。对系统ψ观察所表现的＜A|A＞、＜A|A＞、＜A|A＞、＜A|A＞四种结果，其每一种结果本身都是确定唯一的，有确定的概率和本征值。如果A 和具有本征性（即在相同观测条件下，A 只能表现为A，不可能表现为A，或者A 只能表现为A，不可能表现为A，即A 或A 具有确定性），那么系统观测的关系状态结果要么是＜A|A＞要么是＜A|A＞，A 和A 二者是正交的对立互补关系，二者不构成彼此共存的叠加关系，如电子的上旋和下旋关系，原子的电子磁矩之间关系，其对立性表现为是此则非彼，互补性表现为非此即彼；如果A 或A（或二者同时）具有非本征性（即在相同观测条件下，A既可能表现为A 也可能表现为A，或者A 既可能表现为也可能表现为A，即A 或A 相对于彼此具有不确定性），则A 和A 二者非正交，那么系统观测的结果关系状态要么是＜A|A＞要么是＜A|A＞，A 和A 二者是彼此共存的对立统一的叠加关系，如光子、电子穿过双缝产生干涉关系，以及波粒二象性关系。目前，理论书籍对态叠加原理的表达关注的是(4)式中的本征性结果的第一项＜A|A＞和第四项＜A|A＞，没有关注(4)式中具有非本征性交叉的第二项＜A|A＞和第三项＜A|A＞结果，而将其去掉，但分析双缝干涉时，就必须将其补上。[5]下文将关注这一交叉项的意义分析。

1.2.1 量子态粒子双缝干涉分析

假设一个量子态粒子穿过一个可以产生干涉的双缝，双缝按左右缝来区分。如果粒子量子态穿过双缝时，不用仪器对其观测，只在双缝后面的屏来观测记录，左缝态记作Ls，右缝态记作Rs，则粒子态矢量关系为：

|Ls＞+|Rs＞

其经典确定的结果态（作用一个观察算符）由(4)式可知为：

＜Ls|Ls＞+＜Ls|Rs＞+＜Rs|Ls＞+＜Rs|Rs＞

由于左缝态和右缝态在到达双缝后面的观测屏之前仍处于波包状态，没有塌缩成正交的本征粒子态，左态和右态仍处在非本征的量子叠加状态，二者在相同的观测条件下左态和右态不确定，可以互相转变，表现为非正交关系，因此屏上测量结果为上述展开式中的第二和第三交叉两项，从而在观察屏上产生左右态的干涉结果，观察屏上粒子概率分布就是费恩曼（Feynman）概率幅叠加假设所产生的结果。[8]这个分析结果也说明态叠加原理也应包含非本征的态的叠加，否则无法产生干涉项。同时说明构成粒子量子态波包的各个态是非本征和相互叠加干涉的。

如果用左侧仪器（记作Li）和右侧仪器(记作Ri)分别对经过左缝和右缝的左缝态Ls 和右缝态Rs 进行观测，由于仪器将与粒子量子态发生关系，所以必须加入仪器态矢量，则结果可能是左侧仪器会观察到粒子（粒子波包在左侧仪器处塌缩成经典粒子态），态矢量为|Ls＞|Li＞；也可能是右侧仪器观察到粒子（粒子波包在右侧仪器处塌缩成经典粒子态），态矢量为|Rs＞|Ri＞。由态叠加原理可知二者的态矢量具有叠加关系：

|Ls＞|Li＞+|Rs＞|Ri＞

其经典确定的结果态为对上式作用一个观察算符，作用结果与（3）式到（4）式变换过程相同，展开结果为[6]：

＜Ls|Ls＞＜Li|Li＞+＜Ls|Rs＞＜Li|Ri＞+＜Rs|Ls＞＜Ri|Li＞+＜Rs|Rs＞＜R i|Ri＞

由于左侧仪器观察到粒子，则右侧仪器就不可能观察粒子（其观察到粒子的态对应左侧仪器未观察到粒子的态，与左侧仪器观察到粒子的态二者本征正交），反之亦然，左侧仪器观察到粒子的态与右侧仪器观察到粒子的态二者本征正交（同时，塌缩在左侧仪器和塌缩在右侧仪器两个经典粒子态也本征正交）。因此上述展开式中间交叉关系的两项不存在，只存在具有本征性的第一项和第四项，即粒子量子态穿过双缝不会产生干涉，波函数也不会产生干涉项，在双缝后面的观测屏上的概率分布是粒子单独穿过左缝与单独穿过右缝的概率和，这个分析结果与费恩曼（Feynman）的概率幅假设一致。[7]

如果在量子态粒子进入双缝前进行观测，且观测到粒子，那么此时的粒子已经塌缩成经典粒子态，它既可能从左缝穿过，也可能从右缝穿过，两个可能的态分别记作|Lps＞和|Rps＞，其经过双缝过程的态矢量叠加表示为：

|Lps＞+ |Rps＞

其经典确定的结果态（作用一个观察算符）由(4)式可知为：

＜Lps|Lps＞+＜Lps|Rps＞+＜Rps|Lps＞+＜Rps|Rps＞

由于观测后塌缩的粒子是具有本征性的经典态，因此，|Lps＞和|Rps＞正交，上式中交叉的第二项和第三项不存在，结果为：

＜Lps|Lps＞+＜Rps|Rps＞

即粒子要么穿过左缝，要么穿过右缝，但不能同时穿过双缝，不会发生干涉，在双缝后面的观测屏上的概率分布是粒子单独穿过左缝与单独穿过右缝的概率和。这也进一步证明经典粒子不是薛定谔方程描述的空间分布的概率波包，而是一个空间实体，不能同时穿过双缝产生干涉，但它具有平面波性质，可以通过单缝发生衍射叠加，在观测屏幕上产生衍射性的概率分布。通过上述分析说明仪器的不同的观测方式决定了粒子量子态波包通过双缝的不同形态。

1.2.2 薛定谔猫态分析

薛定谔猫态争议的焦点是猫最终处于要么死要么活的本征结果态，还是处于既死又活的交叉叠加态。我们只需研究设计的第一个环节放射性粒子与电子开关的态关系就可以说明。

放射源放射粒子和未放射粒子的态矢量分别记作|R＞和|R＞，对电子开关接收到粒子和未接收到粒子的态矢量分别记作|G＞和|G＞，电子开关接收到放射性粒子和未接收到放射性粒子是两种可能性的叠加，由态矢量表示为：

|R＞|G＞+|R＞|G＞

其确定的结果态（作用一个观测算符）为：

＜R|R＞＜G|G＞+＜R|R＞＜G|G＞+＜R|R＞＜G|G＞

+＜R|R＞＜G|G＞

由于电子开关接收到放射性粒子的态和未接收到放射性粒子的态是经典确定的两个本征态，彼此互斥，是此非彼，因此是正交的，所以态矢量|G＞和|G＞正交，上面展开式中中间交叉项不存在，变为：

上式表明放射性粒子与电子开关的作用关系是要么放射被接收要么没放射没有被接收，开关这两种状态是经典本征确定态，二者正交（仪器态为经典态，波函数塌缩即变为经典态，由1.1 中分析波函数塌缩后的态不能用波函数来表达，即经典态不能用波函数来表达，因此，仪器经典态之间不具有量子叠加关系，而是彼此正交的），不存在电子开关既又接收又没接收放射性粒子的交叉叠加关系，因此，电子开关以后的过程环节也不存在交叉叠加关系，而是本征的非此即彼关系，因此薛定谔所设计的猫态仍然是经典的非死即活态二者选一的本征态，而不是既死又活的交叉态。薛定谔的错误在于把(3)式所代表的两种态矢量的可能性的叠加等同于现实态的叠加，认为电子开关接收和没接收到放射粒子的两个态具有叠加性，而实际对(3)式态矢量和作用观察算符后的结果态才是放射性粒子与电子开关现实关系的表达，才是具有现实意义的态，而这两个现实态是本征正交的（电子开关接收到粒子或没有接收到粒子的态都是本征确定的，在外界相同的环境条件下，二者不会随机相互转换），不具有叠加性，电子开关对于放射性粒子等同于一台盖革计数器测量，要么记录到放射性，要么没有记录到粒子，放射性粒子放射或不放射的两种可能态在电子开关处被电子开关态的本征性作用（等同于仪器观测作用）所分割终止，变为确定要么放射要么不放射的二选一态。下面分析的粒子的时空关系和波粒二象性关系具有（4）式中第二项和第三项的交叉叠加关系，反映的才是薛定谔所设想的真正的对立猫态的叠加关系。

1.2.3 粒子的时空属性关系分析

下面在时空二象完备表象系统中分析粒子的时空属性关系。当我们某一时刻对一个特定的粒子量子态波包进行局部有效观测时（即在波包特征尺度内进行观测，如粒子量子态经过双缝时，对其中一个缝进行观测），会有两种随机的可能观测结果：一种可能的结果是量子态波包未塌缩，仪器未记录下任何结果，观测仪器表达为一，空性的结果，因为是有效观测，这种空性也是粒子在观测仪器上的一种表达，反映粒子仍处于量子态波包状态，仅体现空间属性（上文已证明波包未塌缩时，仅具有空间属性）。另一种可能的结果是量子态波包塌缩成粒子态，仪器会产生一条记录，仪器记录下量子态波包塌缩成粒子的结果不是对粒子原态的整体复制，而只是记录了粒子的一条信息，这条信息仅反映了粒子的时间属性。之所以说记录的粒子信息仅具有时间属性，一是被记录的粒子信息是粒子一种因素（历史因素）在时空中的现实反映，具有现实可读性，因此具有时空属性；二是记录的粒子信息不是对粒子原态的整体复制，所记录粒子的空间尺度、位置也只是反映粒子空间属性的一条历史信息，而不是粒子空间属性本身，测量后的粒子态的空间属性和位置已化作空间尺度和位置的信息，不是粒子本身的空间维度存在，因此不具有空间属性，然而粒子被记录的信息仍是粒子因素的现实时空存在，那么粒子信息必然仅具有时间属性。从正面分析，粒子态被观测过程就是粒子的现实态转化为历史（信息）的过程，即是粒子产生过程时间性和粒子原有空间属性消失的过程，原有空间属性转化为粒子的历史位置和尺度信息。因此，粒子被观测结果在时空表象下仅具有时间属性。事实上，粒子的历史只能是时间的函数，由时间来标的，而粒子的历史态在现实空间已不复存在，因而不具有现实空间属性，不能用现实空间来反映。需要进一步说明的是粒子信息产生和记录有空间位置，传播有线路有过程，这都是信息载体承载信息后的表象，而非信息本身，信息是载体承载结构形式背后所蕴含的意义，如载体记录的粒子的历史位置、速度、动量数值，而非载体本身，不具有空间属性。对粒子量子态进行局部有效观测的结果所表现出的这种时间属性和空间属性分别反映这个的粒子量子态进行测量的两种完备的可能结果，即粒子量子态塌缩后仪器与经典粒子态的作用结果，以及粒子量子态未塌缩仪器与量子波包态未产生作用结果。这两个完备的结果态的关系可以运用态叠加原理来表达，那么这两个结果态分别对应反映的是粒子的时间属性和空间属性关系(同样的对象不同的表达方式)也具有这种叠加关系。以t 代表粒子的时间属性，以r 代表粒子的空间属性，二者关系同量子态一样具有矢量叠加关系性质，量子态粒子的时空属性关系在量子层面可以表示为（因为是定性分析，为简洁起见，略去相关系数）：

|t＞+|r＞

其在经典层面确定的观测结果反映了粒子状态的时空属性表象如(4)式（对上式作用一个测量算符）：

＜t|t＞+＜t|r＞+＜r|t＞+＜r|r＞

分析以上四种可能的结果态，＜t|t＞代表粒子在经典层面只有时间属性，没有空间属性，这种粒子物理态现实是不存在的（后面会分析其意义所在）；＜r|r＞代表粒子在经典层面只有空间属性，没有时间属性，这种态现实也是不存在的（后面会分析其意义所在）。由于粒子量子态的空间属性|r＞在对波包局部测量时具有非本征性（|r＞反映粒子量子态未塌缩，仪器与量子波包态未产生作用结果，在相同的测量条件下，|r＞既可能不塌缩仍保持空间属性|r＞，也可能塌缩成仪器与经典粒子态发生作用结果的时间属性|t＞），与时间属性|t＞非正交，因此，观测的结果态的时空完备表象必然是＜t|r＞与＜r|t＞两个交叉项。交叉项＜t|r＞代表粒子空间属性在时间属性上的投影（t 和r 代表两种不同的属性，不是叠加干涉关系，而是投影关系[9]），这符合经典粒子形式，其反映了波包塌缩成经典粒子后的粒子态的时空关系状态，粒子的时间属性是自变量，空间属性是因变量。对于运动的粒子，只有非瞬间，才能体现出空间属性r 在时间属性t 上的投影（如果是瞬间就不能反映出空间属性r 的变化维度，而反映的仍然是粒子的历史空间维度），反映出经典粒子＜t|r＞的时空表象，所以，观测运动的经典粒子必须是非瞬间的连续观测（这也揭示了芝诺（Zeno）飞矢不动悖论的问题所在），观测结果的本征值为经典粒子态的连续的时空轨迹，（时间是自变量，空间是时间的函数，）连续的态之间遵循经典因果规律。＜r|t＞代表粒子的时间属性（对应波包塌缩在仪器上的粒子的结果）在空间属性上的投影，这反映粒子量子态波包相对于测量仪器塌缩成粒子过程中的时空属性关系，塌缩的粒子态之间不具有连续性，对于被观测的特定的波包，空间连续统计观测表现为波包塌缩结果的空间的概率分布，空间是自变量，塌缩的概率结果是空间的函数，各态之间遵循相关性规律，而且这个统计测量结果是完备的，结果具有确定的本征性，其本征值就是波包塌缩的空间概率分布，各空间位置的概率构成一个完备的本征子空间[10]。需要进一步说明的是对于非本征性而言，在相同观测条件下，一次观测结果不确定，所以，对于空间塌缩的位置具有非本征性粒子量子态波包统计测量结果才是完备本征确定的。薛定谔方程描述的波函数对应统计测量的概率结果，这一概率结果具有统计测量（非一次性测量）本征性，因而是经典的，具有时间属性。

由前面分析已知，经典粒子的时空属性关系为＜t|r＞，粒子波包的时空属性关系为＜r|t＞，二者的时空属性关系已经发生翻转，因此，量子理论不可能自然地过渡到经典理论。波函数塌缩即变为经典态，由1.1 中分析波函数塌缩后的态不能用波函数来表达，即经典态不能用波函数来表达，这也说明量子理论和经典理论非一元统一的，而是二元对立互补的，这与以往理论经验有本质不同。

2 波粒二象性关系的分析

下面在波粒二象完备表象系统中分析粒子波粒二象性的关系。波粒二象性直观地描述就是在粒子量子态波包的特征尺度内的某个局部进行一次动量观测，如粒子量子态经过双缝时，对其中一个缝进行观测，如果粒子量子态波包塌缩成经典粒子，仪器就会记录下其释放出的动量，即体现出粒子性因素；如果量子态波包未塌缩，波包以波动的衍射形式从另一个缝通过，仪器没有测量结果，波包就体现出波动性因素（这一点与空间属性一样，波动性在一次观测中不能直接观察到，但也是一种结果表现，只有通过干涉和统计观察才能体现出来）。这两种结果分别对应粒子量子态波包被观测所表现出的粒子性（记作Pp）或波动性（记作Wp）两个可能的结果，其关系可以运用叠加原理来表达。粒子的波粒二象性在量子层面可以表示为:

|Pp＞+|Wp＞

其经典层面观测（对上式作用一个测量算符）结果反映了粒子状态的粒子性和波动性的表象关系，如(4)式：

＜Pp|Pp＞+＜Pp|Wp＞+＜Wp|Pp＞+＜Wp|Wp＞

＜Pp|Pp＞代表单纯的粒子属性态，＜Wp|Wp＞代表单纯的波动属性态。根据量子理论和试验可知，对于一个粒子，单纯的粒子属性态和单纯的波动属性态都是不存在的。由于|Wp＞具有非本征性（相同的测量条件下，也可能塌缩为|Pp＞表象），与|Pp＞非正交，因此，波粒二象性在经典层面观测结果表象只能是上式中两个交叉项＜Pp|Wp＞和＜Wp|Pp＞，且只能通过统计观测才能完备地体现。＜Pp|Wp＞代表波动性在粒子性上的投影，即粒子性决定波动性，代表经典粒子态，其本征值就是确定的动量和波长，由前文1.1 粒子的量子态的时空属性分析此波非概率波，只有通过衍射叠加才能产生概率分布结果，统计观测衍射结果才能体现出粒子性与波动性的关系，即确定的动量决定确定的衍射概率分布，这种波粒关系由德布罗意公式确定；＜Wp|Pp＞代表粒子性在波动性上的投影，即波动性决定粒子性，空间波包塌缩时，塌缩位置和动量值随机，其统计测量结果才体现出本征性，统计测量的本征值就是粒子确定的时空概率分布和动量值概率分布，且时空概率分布决定动量值概率分布，可以通过双缝干涉统计观测到波动性与粒子性的关系，即观测屏上确定的粒子波动干涉条纹分布对应确定的动量值概率分布，二者的波函数是傅里叶变换关系。根据以上分析，需要说明的是不要将粒子性、波动性同粒子态和波动态混为一谈，前者反映的是单一属性，后者是前者两种单一属性的叠加，即粒子态既具有粒子性，同时具有波动性，可以产生衍射，二者关系由德布罗意波粒二象性公式描述；波动态既具有波动性，同时具有粒子性，波动态必须通过波包塌缩成粒子才能体现出干涉条纹，二者波函数是傅立叶变换关系。

3 时间具有方向性分析

下面运用叠加原理对时间的演变方向进行分析。我们将粒子的时空属性分析转化为对粒子的历史、现实和未来关系的分析。从历史、现实和未来体系来分析，对于粒子的量子态波包局部进行有效观测，一次观测到粒子态的记录结果代表粒子的现实性塌缩成历史的确定性信息，即观测记录结果反映的是粒子的历史，而不是现实；一次观测到粒子波包的空态，没有产生记录结果，代表粒子还处于不确定的未来状态，观测的结果反映的是粒子的未来属性，这种状态不是粒子的消失，而是粒子尚未作用于观测者，相对于观测者还处于未来不确定状态。对于粒子量子态局部观测而言，在相同的观测条件下，一次观测既可能产生塌缩的反映粒子历史属性的结果，也可能是未塌缩的反映粒子未来属性的结果，根据(3)式，粒子的历史态矢量（记作|H＞）和未来态矢量（记作|F＞）叠加表示为：

|H＞+|F＞

其经典层面表象结果由(4)式可知为：

＜H|F＞代表未来属性在历史属性上的投影关系，反映经典粒子态在历史属性和未来属性体系的现实表象；＜F|H＞代表历史属性在未来属性上的投影关系，反映粒子量子波包态在历史属性和未来属性体系的现实表象。历史和未来是人类意识概念，只对意识体有意义，如果我们把历史和未来也看成是一种广义的态的话，那么，＜H|H＞代表历史属性态，即仪器记录信息态，具有确定不变性；＜F|F＞代表未来属性态，即仪器无记录信息态，具有不确定性。由1.2.3 分析的观测结果知道，|t＞代表粒子波包态塌缩成粒子态记录的态矢量，|r＞代表粒子量子波包态未塌缩对应的态矢量。二者构成关系如下：

|t＞+|r＞

在经典层面确定表象为：

＜t|t＞+＜t|r＞＞+＜r|t＞+＜r|r＞

比较上述两类分析，发现描述的是同一对象同一性质过程，只是一种用时空属性来描述，另一种用历史和未来属性来描述，二者的对应关系是：|H＞等同于|t＞，|F＞等同于|r＞，＜H|F＞等同于＜t|r＞，反映经典粒子态在经典环境下的现实态，＜F|H＞等同于＜r|t＞，反映粒子量子态波包在经典环境下的现实态。＜H|H＞等同于＜t|t＞，代表观测记录到粒子的历史信息态，＜F|F＞等同于＜r|r＞，代表观测仪器在观测位置持续统计观测尚未观测到现实存在的粒子，二者之间尚隔空间，粒子相对于观测者处于未来状态。粒子的历史属性态和未来属性态都是观测仪器的观测粒子的结果，并不是粒子现实的态，这两个结果相对于观测仪器是分立的，且只有观测者为有意识体才具备识别历史属性态和未来属性态意义和运用能力，粒子相对于自己只有现实态（历史与未来，时间与空间是交叉叠加的），而粒子现实态相对于观测仪器而言就是其观测作用过程。由此可以说，对于观测者而言，粒子的历史属性态是纯时间属性态，粒子的未来属性态是纯空间属性态。粒子的时间方向性对于观测者来讲就是经典粒子由现实态塌缩到历史属性态的过程，即由＜H|F＞变为＜H|H＞过程，即由＜t|r＞变为＜t|t＞过程，也就是粒子的空间属性|r＞塌缩为时间属性|t＞的过程。而由前文1.2.3 粒子的时空属性关系分析可知粒子量子态波包塌缩为经典粒子的时空表象过程，对于观测者的一次性观测（统计观测不反映单一波包塌缩实际过程）反映的时空表象就是空间属性|r＞塌缩为时间属性|t＞的过程。量子力学已给出明确结论，测量粒子量子态波包塌缩为粒子的过程是一个熵增的过程[11]，因此，对应的|r＞塌缩为|t＞的过程也是熵增的过程。所以，时间的方向性即由＜t|r＞变为＜t|t＞过程，也就是|r＞塌缩为|t＞的过程，与熵增的方向性一致，即时间过程必然伴随熵增，熵增不可逆，所以时间过程具有不可逆的方向性。理论公式中的时间不能体现出方向性，是因为理论公式是建立在把全部客观环境的未来理想化为具有历史确定性的假设基础之上，把未来状态历史化了，即由现实的＜H|F＞态变为确定的历史信息＜H|H＞态，否定了未来属性的多种真随机可能性，从而体现出拉普拉斯的决定论结果。而历史信息态不会体现出熵增趋向，历史信息态如录影可以反向观看（现实态则不可以，因果不可逆），因此，无法体现出时间的方向性。理论公式就是对客观对象的未来进行了确定化、历史化的理想表达，忽略了客观的多种可能性（真概率随机性，如人为的主观干扰），其有效性是建立在未来客观条件高概率稳定的预期基础之上的，对于未来可控或高概率可期的环境，理论公式预期有效，对于未来随机变化较大的环境，理论公式则无法准确预期，必须引入时间不可逆的概率因素。

4 量子态叠加原理的逻辑意义

量子力学一个基本原理就是量子态叠加原理。这一原理可以简单地表述为：对一个系统在相同的条件下进行观测，其观测结果既可能是A 也可能是A（A 和A 构成完备结果），那么相对于该系统A 和A 具有如下态矢量叠加关系：

由（3）式和（4）式可知，被观测系统的确定结果状态必为以下四种可能状态之一：

|A＞+|A＞代表由|A＞和|A＞构成的对立完备关系。这个体系展开为＜A|A＞、＜A|A＞、＜A|A＞、＜A|A＞四种可能的关系状态结果。由前文对量子态叠加原理的分析可知，如果A 和A 具有本征性，那么系统观测的关系状态结果要么是＜A|A＞要么是＜A|A＞，A 和A 二者是正交的对立互补关系（如电子的上旋和下旋关系，观测电子穿过双缝的左右结果关系）；如果A 或A（或二者同时）具有非本征性，则A 和A 二者非正交，那么系统观测的关系状态结果要么是＜A|A＞要么是＜A|A＞，A 和A 二者是非正交的对立统一关系（如未经观察的电子穿过双缝产生干涉结果关系，前文分析的粒子态的时空关系及波粒二象性关系）。

量子态叠加原理应用的条件就是对一个系统在相同的条件下进行观测，其观测结果既可能是A 也可能是A，系统状态表象具有不确定性（系统相对于观测方式状态非本征）。其本质与系统的具体的属性无关（如粒子的时空属性、波粒二象性、电子自旋、双缝干涉），而是与简并的形式系统非本征性相关，即与简并形式系统的不确定性表象相关。如果一个形式系统可以用A 与A 两个对立完备因素来完备表达，并且该系统相对于A与A 的表象既不能必然表象为A，也不能必然表象为A，而是既可能表现为A，也可能表现为A，这个形式系统相对于A 与A的表象是非本征不确定的，那么，该形式系统在可能性层面就具有A 与A 的矢量叠加关系，表象满足(6)式关系，在确定性层面的表象变换为(7)式关系。这样叠加原理就拓展为一种形式逻辑公理。

形式逻辑系统也存在上述非本征的不确定性情况。仅具有确定性的传统形式逻辑系统是不完备的，应该拓展到这种具有不确定性逻辑关系的系统，从而建立起既包含具有本征性的传统形式逻辑系统又包含具有非本征性逻辑系统的完备逻辑体系。由此提出如下广义逻辑公理即二元对立完备逻辑公理：

广义形式逻辑系统包含两个对立完备形式A 和A（如几何系统分为欧氏几何和非欧几何，实数系统分为有理数和无理数以及悖论系统包含肯定与否定关系），且该系统关于A 和A 形式的表象既不能必然表象为A，也不能必然表象为A，而是可能表象为A，也可能表象为A（表象为A 或A 均不具有必然性，因而皆为真可能性，由模态逻辑可知对立的真可能性必然同真）由前面分析可知，该形式系统就具有|A＞+|A＞矢量叠加关系，由(6)式和（7）式可知，其确定的逻辑关系（非集合关系）完备表象结果为：

如果A 和具有本征性（自身同一确定性），则(8)式的结果为以下两项：

那么该系统A 和A 的表象是正交的对立互补关系，即A 成立的情况下，A 不成立；A 不成立的情况下，A 则成立。其中正交对立关系反映了二者无自相矛盾性和同一性（本征确定性），互补关系反映了二者完备的排中性。这正反映了构建传统形式逻辑的三个基础定律——（无）矛盾律、排中律、同一律。因此，＜A|A＞和＜A|A＞的关系反映的正是传统形式逻辑关系，即传统形式逻辑是建立在对立元素具有本征性对立基础之上的，对立元素表现为对立互补关系。

如果A 或A（或二者同时）具有非本征性（具有可以转化为对立面的不确定性），则(8)式的结果为以下两项：

A 和A 二者非正交，那么该系统A 和A 的表象关系为要么是＜A|A＞要么是＜A|A＞，A 和A 二者构成非正交的对立统一关系。其中＜A|A＞表示A 成立则A 也成立，＜A|A＞表示A 成立则A 也成立，A 和A 二者构成对立统一的悖论关系，这种关系恰恰不符合传统形式逻辑的三个基础定律——（无）矛盾律（本身就是矛盾）、排中律（本身不完全属于A 也不完全属于A，而是居中）、同一律（A 或A，或二者同时具有非本征的相互转化性）。由前面分析可知，时空关系和波粒二象性关系正是这种对立统一的悖论逻辑关系的客观实在表现。综上所述，二元对立完备逻辑公理可以完备地反映A 和A 的矛盾逻辑关系。由此说明矛盾具有两种基本形式：对立互补形式和对立统一形式，前者反映了传统形式逻辑所描述的本征性元素所具有的客观规律性，后者体现了辩证逻辑矛盾对立统一的实在性。在哲学方面，一个反映的是形而上学静止的矛盾关系，另一个反映的是辩证运动的矛盾关系。同时我们也看出本征性（确定性）和非本征性（不确定性）是比矛盾更基本的科学概念。下面运用二元对立完备逻辑公理进行实例分析。

4.1 实数系统表象分析

以实数系统（记作S）为例，S 系统由有理数系统（记作Y）和无理数系统（记作Y）完备构成。那么，S 在Y 和Y 组成的表象系统中展开，既不能必然表象为Y，也不能必然表象为Y，而是可能表象为Y，也可能表象为Y，S 具有如下矢量叠加关系：

|Y＞+|Y＞

由（8）式可知，其确定的逻辑关系的完备表象结果为：

＜Y|Y＞+＜Y|Y＞+＜Y|Y＞+＜Y|Y＞

由于有理数系统Y 与无理数系统本征正交（二者具有确定不变性，不具有互相转变性），由（9）式可知S 的逻辑表象结果为：

S→＜Y|Y＞+＜Y|Y＞

即实数系统S 按有理数系统Y 和无理数系统表象展开，要么表现为有理数系统结果＜Y|Y＞，要么表现为无理数系统结果＜Y|Y＞，二者对立互补，共同构成实数系统完备表象。

4.2 逻辑悖论分析

罗素理发师悖论分析：一个理发师承诺他仅给村里所有不自己理发的人理发。那么，他是否应该给自己理发呢？如果给自己理发，他就不属于不自己理发的人，按约定就他不应该理；如果不给自己理发，他就成为不自己理发的人，就应该给自己理发，这就出现矛盾。[12]理发与不理发属于经典世界里的本征态矛盾行为，根据前面分析，本征态矛盾正交，二者互斥，不能共存，只能是对立互补关系，不是彼此共存的对立统一关系，不能同时存在。应该遵守传统形式逻辑，不能自相矛盾，其出现矛盾，依据反证法，逻辑是错误的，并不是真正意义上的悖论，属于不符合逻辑的不具有客观性的主观臆构。对于悖论：“这句话是假话”，则是真正意义的悖论。具体分析如下：

如果这句话是真话，按其表达的语义则为假话，如果这句话是假话，与其语义表达一致，则这句话又变为真话，因此，不能确定这句话为真或为假，即可能为真也可能为假。这句话既可能真（记作T），也可能假（记作f），T 和f 构成矢量叠加关系：|T＞+|f＞，且在这句话里真和假，皆具有非本征性（真包含真的假，即包含假；假包含假的假，即包含真）。根据上述二元对立完备逻辑公理(10)式，二者确定的逻辑关系表达为：

＜T|f＞+＜f|T＞

其逻辑意义是如果真则假，如果假则真，这里的真假构成了对立统一的矛盾关系。谎话悖论中的真和假皆为非本征性，物理电子过双缝的干涉也为双非本征现象。物理中的时空属性关系、波粒二象性关系则为单非本征现象。

由上述分析可知，悖论的逻辑形式就是＜A|A＞或＜A|A＞这种对立统一形式，电子过双缝干涉，以及前面分析的粒子时空属性、波粒二象性等正是其现实物理意义所在。因此得出结论：粒子的时空关系和波粒二象性关系具有共同的悖论逻辑关系。

5 结论

本文运用狭义相对论异地不同时性证明了粒子量子态不具有时间属性，只具有单纯的空间属性；依据量子态叠加原理给出粒子的时空属性关系和波粒二象性关系的对立统一定性表达形式；运用粒子时空关系的数学定性表达形式和粒子量子态波包塌缩熵增定律给出了时间的方向性即是熵增的结论；将量子态叠加原理拓展到数理逻辑领域，提出了二元对立完备逻辑公理，最终给出了粒子量子态的时空属性关系和波粒二象性关系共同具有对立统一的悖论逻辑关系的结论。