股市因子投资发展史梳理

文/岳阳（武汉大学经济与管理学院）

一、对收益率的初步认知

（一）收益分解——α收益和β收益

1964年，华盛顿大学教授William F. Sharpe在Journal of Finance上发表了一篇论文，将资产收益分为两大部分：α收益和β收益。其中，β收益代表资产和市场共同波动的收益，β＞1，意味着资产比市场投资组合有更高的波动，反之则更小；α收益代表资产收益中和市场投资组合波动无关的部分，α＞0，表示资产收益存在着不能被市场投资组合收益所解释的部分，α=0，则表示资产收益可以完全被市场投资组合所解释。这也就是著名的CAPM模型。

这种对资产收益的拆分具有里程碑的意义，它使得人们对资产的收益有了系统性的、结构性的认知。而不出意外的，α收益作为不能被当前市场组合所解释的收益，对投资者而言充满了神秘性和诱惑力，也成为随后几十年投资者和研究者竞相研究的目标。

（二）研究动机— —α收益的“吸引力”

α收益代表了“尚难以确定的、大小未知”的收益，这种不确定性为人们带来了喜悦和担忧。一方面，对投资者而言，尤其是短期投资者，通过“低买高卖”获得暂时的收益是一种获利方式。但人们迫切地想知道哪些资产拥有α收益，从而在市场收益的基础上获得更多；另一方面，对于资产定价的人员来说，α收益的存在意味着当下定价模型的不完善，人们没有捕捉到资产收益变化的根源，又或者没有找到合适的模型去拟合资产收益，从而对未来做出合理预测。因此，伴随着这样的诱惑和不足，无论是业界还是学界，一场揭开α收益神秘面纱的运动就此展开。

二、异象、模型与α收益

（一）推陈出新——FF-3因子模型和FM回归

在金融市场中一个重要问题是解释为何不同资产会有不同的收益率，什么样的变量可以更好地代理资产收益，如何使预测更为精准一直都是众多研究人员的重要课题。

随着时间的推移，人们发现CAPM并不能很好地解释资产收益，也即α收益依然存在。模型上的重大进展可以从经典的Fama French三因子模型说起。而它的提出者正是时至今日仍在不断推陈出新的Fama和French。基于当时的研究，两人最终选择市值和账面市值比两个因子，作为市场因子的补充，形成了FF三因子模型。将美国股票市场作为研究对象，他们发现，FF三因子模型可以很好地解释股票收益，α趋近于0。这意味着市场组合、市值和账面市值比可以很好地代理股票收益。由此，最初的异象因子出现了。

而Fama和French的论文研究方法一时成为众多研究者竞相借鉴的方法。现简单介绍如下：首先获知某因子可以有效预测股票收益，则可以按照该因子对股票进行由高到低的排序，并等分为10组（研究中还可以分为5组，美国股市的研究常常按照市值大小分为大中小三组）。做多因子最大的一组，做空因子最小的一组，两组收益率之差就是该因子的当期收益。为了避免不同因子之间的影响，需要事先基于市值和账面市值比对股票进行交叉分组，再构造相应的“高减低”投资组合。由此，我们可以获得最经典的SMB和HML。这种分组买卖的方法计算简单、易于操作，受到广大研究者的青睐。

此外，构造出新的因子后，与股票收益进行回归，通过检验截距项是否显著异于0，也即α收益是否显著存在，可以判断选定的因子是否足够解释股票的收益。而作为这一系列研究的开端，FF3因子也成为其后众多因子模型的基础——研究者不只要获得不显著的α，还要证明自己提出的新因子不能被经典的FF3因子所覆盖，否则新因子就失去了提出的意义。

此外，在研究过程中，一种在后期被多次借鉴的检验截面之间收益差异的办法出现了——Fama Macbeth回归（以下简称“FM回归”）。这个方法最早于1973年被Fama和Macbeth提出。

FM回归为两步回归。分别是时间序列回归和截面回归。

首先，通过时间序列回归得到个股收益率在因子上的暴露βi：

其中，为资产i在时期t的收益；f可以为多个因子。本回归可以按照移动窗口处理，这样每一期的系数都会不同。

接着，通过截面回归获得因子收益率λt：

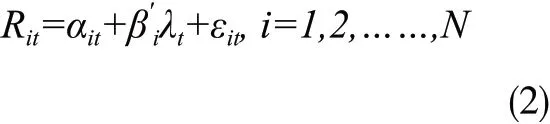
也就是说，如果有T期，则进行T次截面回归，此时会获得一系列截距和系数，做时间平均如下：

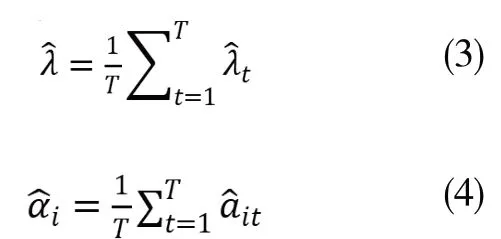
通过检验系数的显著性，就可以知道因子在指定样本期内是否拥有显著的收益。根据上面的方法可知，FM回归的最大优点是它排除了残差截面相关性对标准误的影响，传统截面回归方法中回归系数的standard errors会因为残差收益率在截面上的相关性而被低估，这将导致参数显著性（如t值和置信区间）计算受到影响。

（二）多项推广——因子动物园的丰富

然而好景不长，随着时间的流逝，人们发现FF3因子模型的解释能力开始下降，α收益再次出现。寻求新的异象和更有效的模型迫在眉睫。从Fama French三因子模型，到Carhart四因子模型、Fama French五因子模型、q4因子模型以及拥有盛名的q5因子模型，因子模型经历了长足发展。可以看到，在异象因子的发掘和模型的建立上，有如下特点：首先，传统研究对异象的挖掘是充分建立在已有研究结果和经济学理论上的；其次，经典的因子模型追求“少而精”，研究人员力求以最少的有效因子去刻画股票收益波动的来源。

然而，算力的大幅提高和财务数据与市场数据的日益丰富，使得新因子层出不穷，“因子动物园”论断的提出指出了现在因子个数繁杂的事实。如何在这样的海量数据中“由繁入简”，这一问题在第四部分进行讨论。

如果说Fama和French为因子的构造开辟了先河，那么Fama Macbeth回归则为多因子的同时检验提供了思路。根据FF3因子的构造过程不难发现，当因子个数少时，做交叉分组尚可完成，但随着需要检验的因子个数的增多，交叉分组会使得组合个数大大增加，不利于分析。Fama Macbeth回归的提出解决了这一问题：多元回归的天然特性使得其可以一次性检验多个因子，避免了分组的尴尬。时至今日，FM回归可以有两种作用：一种是样本内预测，通过对样本期内的股票收益与因子进行回归，观察系数是否显著可以知道该因子与收益是否具有显著相关性；另一种是样本外预测，通过对训练集中的收益与因子进行回归，可以获得因子与收益的关系，从而利用当期因子数据可以对未来收益做出预测。Fama Macbeth回归作为线性模型的代表，为其后的线性预测模型提供了基本的研究方法和操作规范。

三、异象的发掘和检验

对异象因子的挖掘需要建立在理论之上，不能做单纯的数据挖掘。因为在海量的数据中，要找到和收益有高度相关的“伪因子”并非难事，但如何能够找到科学的有理论依据的因子才是研究人员真正关心的问题。

对于一个特征而言，如果基于该特征投资组合的收益率不能被用于资产定价的多因子模型所解释，那么该特征就称为一个异象。从数学上看，该投资组合有着传统定价模型所无法解释的α收益。将该投资组合收益率作为被解释变量，传统定价模型中的因子收益率为解释变量，进行时间序列回归，如果截距项α显著不等于0，则该特征就是一个异象。

而一个异象要成为真正的因子则需要通过因子检验。就因子检验而言，每一个因子的提出必须要经过层层检验，才可称其为新的因子。有两个基本的判断依据：①该异象可以对被解释资产的收益率有显著贡献，也即该异象处于回归方程的右侧；②这种贡献是一种增量贡献，也即是超过已有解释因子的额外贡献。而提到异象的有效性，就不得不引入Hou et al(2018)这篇长达115页的论文，也是RFS历史上最长的论文之一。在这篇文章中，作者复刻了452个已经被提出的异象。针对数量庞大的异象，作者发现，有65%的因子失去了预测效果（在t值为1.96的条件下）；而将t值提高至2.78后失效因子个数比例增多为82%。

此前之所以产生如此多的异象，一方面是由于数据挖掘，另一方面可能和右侧的定价模型相关。如果仅仅以CAPM作为定价模型，则很容易产生显著不为0的α收益。

四、异象信息的利用

前面提到，目前异象因子众多，且许多因子在被发现之后，被投资者不断买卖，其收益预测能力出现大幅下降。目前到底什么样的是有效因子需要进一步甄别，且财务信息与市场信息披露逐渐规范，这其中的巨大信息量促使人们希望能更高效的利用信息。由此，一系列关于信息的聚合和利用的方法被应用在金融领域上。

（一）个数惩罚——对传统回归的改进

在“因子动物园”中，有的因子在预测收益上作用更大，而有的因子作用更小，甚至已经失去了作用。然而因子个数过多有可能会造成过拟合，解决方法之一就是正则化。

正则化是一般损失函数和正则化项的双重体现。一般损失函数是指均方误差，即预测误差的平方的均值；正则化项则有两种，一种是L1范数正则化，也即LASSO（Least Absoulute Shrinkage and Selection Operator），其代价函数为：

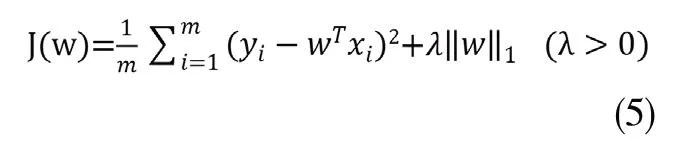
另一种是L2范数正则化，也即岭回归（Ridge Regression），其代价函数为：

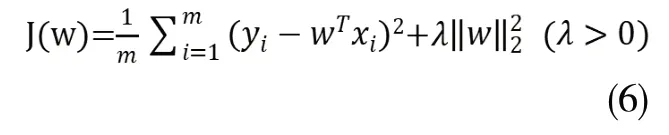
而将L1与L2范数相结合，就可以得到弹性网络算法，其代价函数为：

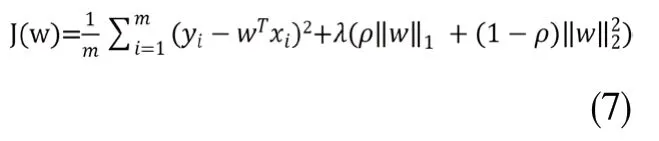
无论是L1范数还是L2范数，都有助于降低过拟合风险，获得稀疏解。（L1范数更有可能获得稀疏解）

LASSO等正则化方法在实证研究中也有不少应用。Rapachet al.(2013)利用LASSO研究了美国市场与世界市场之间相互影响的关系；Huang & Shi(2016)利用adaptive group LASSO 构建了宏观经济变量，并研究债券风险溢价的决定因素；Freyberger et al.(2020)通 过Group LASSO的方法证明现有因子集中只有一部分因子是有效的。可见，由于有回归的基础，正则化方法依然可以判别变量之间的“因果关系”，又因为新惩罚项的加入，从而可以对变量做出筛选。

（二）信息聚合——降维技术的新应用

研究的初期人们把目光放在异象因子本身。人们从“信息携带量”的角度出发，研发出一系列辨别因子携带信息并加以提取的技术。甚至从某种意义上讲，FM回归也是对异象因子信息的提取：β系数越高，模型就认为该因子越重要。而最近被应用较多的技术之一为主成分分析（Principal Component Analysis，PCA）。其原理如下：

PCA，顾名思义，是对已有众多信息的充分提取，借助一定的手段对已有因子进行线性组合，从而在最大程度保留原有信息的前提下实现降维。该方法在学术研究中应用十分广泛。

后来随着技术的成熟，研究人员意识到提取异象因子内的信息不是根本目的，最终我们希望得到的是对资产未来收益的优良预测。因此，此前只考虑因子本身携带信息的做法并不能够捕捉因子信息和资产收益之间的关系。提取主成分后，被舍弃的信息中或许包含可以预测未来收益的成分，而主成分中也有可能存在对预测收益用处不大的部分。人们在PCA的基础上进一步改善，考虑因子和未来收益之间的关系，得出偏最小二乘法（Partial Least-square Method，PLS）。Light et al. (2017)创造性地将PLS方法用于根据横截面公司特征估算单个股票的预期收益，最终得出因子信息聚合作用下可得到更有效的预测结果。通过构建出收益率和因子之间的关系，从而大大提高了因子预测能力，Light表明，相比FM回归和PCA，PLS拥有更出色的预测能力。

五、异象因子在中国的检验

大部分异象的提出都是基于国外市场的，异象在中国是否有效就成为中国学者关心的问题。

较为典型的是Liu et al.(2019)(Size and value in China)文章。作者在文章中重新提出了中国三因子模型。其中作者将价值因子账面市值比(BM)替换成市盈率的倒数(EP,Earnings-to-Price)。这样做参考了Fama & French(1992, 1993)的思路，采用“跑马赛”的方法，以一批价值因子为指标，利用Fama Macbeth截面回归逐月分析，最后发现EP的预测能力最强，所以作者最后选定此指标（表1）。

表1 CH-3因子的构造

两个因子构造公式为：

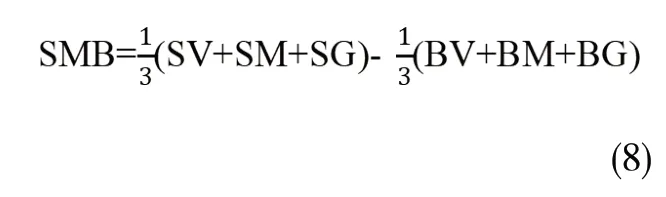
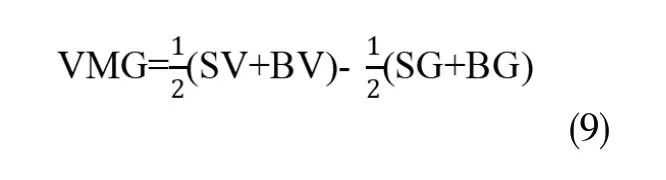
对于因子模型而言，解释收益均值是一个目的，解释收益变化是另一个目的。作者通过对CH-3因子模型对收益的回归，计算出R2。结果发现SMB和VMG因子对于提高R2的确有显著作用。

作者在文章中提出了适合中国股市的三因子模型，与之形成对标的是FF三因子模型。作者希望检验CH-3模型是否会优于FF-3模型。通过模型对另一个模型内部单因子的回归发现，CH-3可以很好地解释FF-3内部因子，也即没有显著的α，但反之不可以。此外，要同时检验一个模型是否可以同时解释另一个模型的所有因子，需要用到GRS检验。GRS检验可以同时观察多个收益率数据是否可以同时被某个模型所解释，其原假设为截距项联合为0。结果显示，FF-3模型可以被CH-3所解释，p值为0.41，而CH-3则不能被FF-3解释，p值小于10-12。

仅仅两个模型彼此检验是不足以支撑CH-3模型是适合中国市场的模型，还需要检验它对异象的解释能力有多大。作者经过筛选挑选出10个基于CAPM有显著α收益的异象，并分别用CH-3和FF-3对其定价，结果表明CH-3的表现远胜于FF-3，前者可以解释8个异象，而后者只能解释3个。此外，考虑到依然存在CH-3不能解释的异象，作者新纳入换手率因子，将其扩展至CH-4，并再次检验其对异象的解释能力，结果发现解释能力获得了提升。

可以说Liu et al.(2019)这篇论文提供了在中国市场做因子检验的一个范本，内容涉及因子的构建、模型的对比及后续检验。其构建的CH-3因子也被多次引用用于检验其他模型的收益是否显著。

六、结论

本文梳理了因子投资的发展历程，从分解股票收益、寻找α收益，到传统定价模型的提出以及异象因子的不断增多，延伸至对因子有效性的诸多检验方法和对信息的高效利用方法，最终落脚到中国股市的异象因子的检验，在时间维度上从前至后论述了因子检验相对完整的方法论。

在投资方法上，我国市场参与者早期以传统投资方式为主，分别是基本面分析和技术分析。前者通过宏观经济数据与公司财务数据等分析公司的健康状况和成长性，后者则从历史市场数据出发，以市场价格及交易量为基础对股价未来走势做出判断。但在有效市场假说的理论下，随着市场有效性的增强，公开信息将越来越难以提供超额收益，而随着监管力度的增大，非公开信息也愈发难以获得。而新兴的量化投资方式则可通过海量的数据及多重模型，在公开数据中挖掘其背后的隐藏信息，创新空间巨大。

量化投资与传统投资既有共通之处，又有着自身的独特优势。二者均认为市场是不完全有效的，因此有动机追寻超额收益。但二者在选股方法、获取信息的渠道和投资风格等方面均存在差异。在股票选择上，传统投资更依赖于人的主观判断，而量化投资则基于数学模型加以选择；在获取信息方面，传统投资看重宏观基本面的定性分析，而量化投资从海量的财务及市场数据出发进行信息提取；就投资风格而言，传统投资偏向于长期，而考虑到数据的不断变化，量化投资则更偏向于短期；此外，当市场整体呈现颓势之时，传统投资的优势难以为继，而量化投资则可在市场低迷之时有效寻求到α收益。因此，作为不断成熟，持续发展的投资方法，量化投资相比于传统投资方式呈现出更稳定、更客观等诸多优点。在当下投资热的背景下，量化投资使得投资合理化、获利最大化、决策中立化成为可能。量化投资依托于数学模型和计算机技术，前者保证投资有理可依，后者的不断发展则确保投资决策及时有效。鉴于基本面投资和量化投资各有优势，新的研究方法应运而生——基本面量化投资。它以基本面数据为基础，运用量化投资的技术，将二者的优势有机地结合起来，正逐渐成为更受投资者青睐的工具。