概率法气藏储量计算中评估参数分布函数的确定
2022-01-18任超群
张 磊 潘 燕 任超群 张 华 吴 娟
(中海石油(中国)有限公司湛江分公司, 广东 湛江 524057)
常用油气储量计算方法有类比法、物质平衡法和容积法等。类比法只用于钻探前的远景储量估算。物质平衡法,是指在油气藏开采一段时间之后根据压降、采油曲线等作出油气储量评价。由于缺乏较长时期内的生产数据支持,物质平衡法不适用于油气藏评价阶段的储量估算。容积法,是计算油气藏地质储量的主要方法,适用于不同的勘探开发阶段、圈闭类型、储集类型和驱动方式。该方法是采用油气藏静态资料对储量进行评估,适用性较好,实际应用最广泛。容积法又可分为确定法和概率法:采用确定法时,各参数及储量的计算结果均为一个确定的值;采用概率法时,可计算出各参数的分布范围[1-6]。通过概率法计算的储量估计值能更准确地反映储量潜力,目前该方法已成为资源量、储量计算的常规方法之一[7-11]。
贾成业等人分别运用确定法和概率法计算地质储量,通过对比发现概率法在储量风险评估方面更具优势[12]。覃利娟等人应用概率法对涠洲A油田进行了储量估算,讨论了该油田储量的可靠性[13]。谢寅符等人分析了概率法和确定法在储量评估中的差异,指出了两种方法的适用范围以及概率法储量评估中参数函数选取方法的重要性[14]。涂乙等人在概率法储量评估中引入形状因子以减轻构造形状对储量估算结果的影响,并结合地质参数对储量结果进行敏感性分析,为开发方案提供理论依据[15]。
东方A气田为构造岩性边底水气藏,其分布主要受岩性控制,其中有钻探井、评价井共计4口,各井相距2.2~3.0 km,均处于开发初期。目前,该气田各井资料较少,这4口井钻遇的气水界面差异直接体现为含气砂体分布较为复杂以及发育多套砂体。含气砂体分布范围及含气饱和度等储量计算中所涉及到的参数都存在不确定性,导致地质储量预测结果也存在不确定性。本次研究将以该气田为例,讨论概率法油气储量计算及其评估参数分布函数的确定。
1 概率法油气储量计算
1.1 原理
基于概率法的油气储量计算主要是以随机变量为对象,以概率论为基础,重点研究目标构造单元与容积法储量计算公式中各参数的函数分布规律及概率特征,提供储量概率分布曲线或不同可靠程度的储量数值。以容积法为基础,从概率分析为手段,量化储量的不确定级别。天然气地质储量计算公式如下[1-3]:
G=0.01·A·h·φ·Sgi/Bgi
(1)
(2)
式中:G—— 天然气储量,108m3;
A—— 含气面积,km2;
h—— 有效厚度,m;
φ—— 有效孔隙度,%;
Sgi—— 原始含气饱和度,%;
Bgi—— 原始天然气体积系数;
T—— 平均地层温度,K;
Tsc—— 地面标准温度,K;
psc—— 地面标准压力,MPa;
pi—— 平均气藏的原始地层压力,MPa;
Zi—— 原始气体偏差系数。
1.2 样本数据分析
根据东方A气田的砂体分布特点,对0气组砂体及Ⅰ气组a、b、c砂体计算单元储量进行研究,进而计算和评估全气田的储量。图1所示为概率法储量计算的技术路线。

图1 概率法储量计算的技术路线
研究对象包括:4口钻探井、评价井,即D-1井、D-2井、D-3井、D-4井;4套含气砂体,即0气组砂体,I气组a、b、c砂体;4类储量参数,即含气面积(A)、有效厚度(h)、有效孔隙度(φ)、含水饱和度(Sw);4种分布函数,即三角函数、正态函数、对数正态函数、贝塔分布函数。
确定样本数据后,根据数据特点并结合数理统计分析,最终确定各气组储量参数及其分布函数(见表1)。

表1 各气组储量参数及其分布函数
2 储量参数概率分布函数的确定
2.1 含气面积概率分布函数
依据流体界面、砂体分布范围、属性分布规律,确定含气面积的大小。根据最小振幅属性,以最好属性为边界圈定最小含气面积,以钻遇的流体界面圈定期望含气面积,以岩性边界圈定最大含气面积,最后得到各砂体的含气面积数据。含气面积样本数据为3个,采用三角概率分布函数进行计算,最后分别将每个砂体含气面积的最小值、期望值、最大值输入模型。
2.2 有效厚度概率分布函数
在厚度图上设置虚拟井,分别计算每口虚拟井的有效厚度,将所有井的有效厚度作为样本数据进行分析。根据有效厚度样本数据的特点,采用三角函数和贝塔概率模拟其分布函数(见图2),并绘制有效厚度概率分布图(见图3)。
2.3 形状因子分析
本次概率法储量计算中,着重考虑了气藏的形状因子(见图4)。对于形状因子,一般按照气藏模型的不同形状来确定:角锥体气藏模型,适用于底水气藏或块状体储层,如0气组砂体;棱柱体/圆柱体气藏模型,适用于边水或层状等效体,如I气组a、b、c砂体。
根据气藏储集层厚度与形状因子关系图版,得到4套砂体(0气组砂体及I气组a、b、c砂体)的形状因子(见表2)。

图2 砂体有效厚度贝塔概率分布函数模拟分析结果
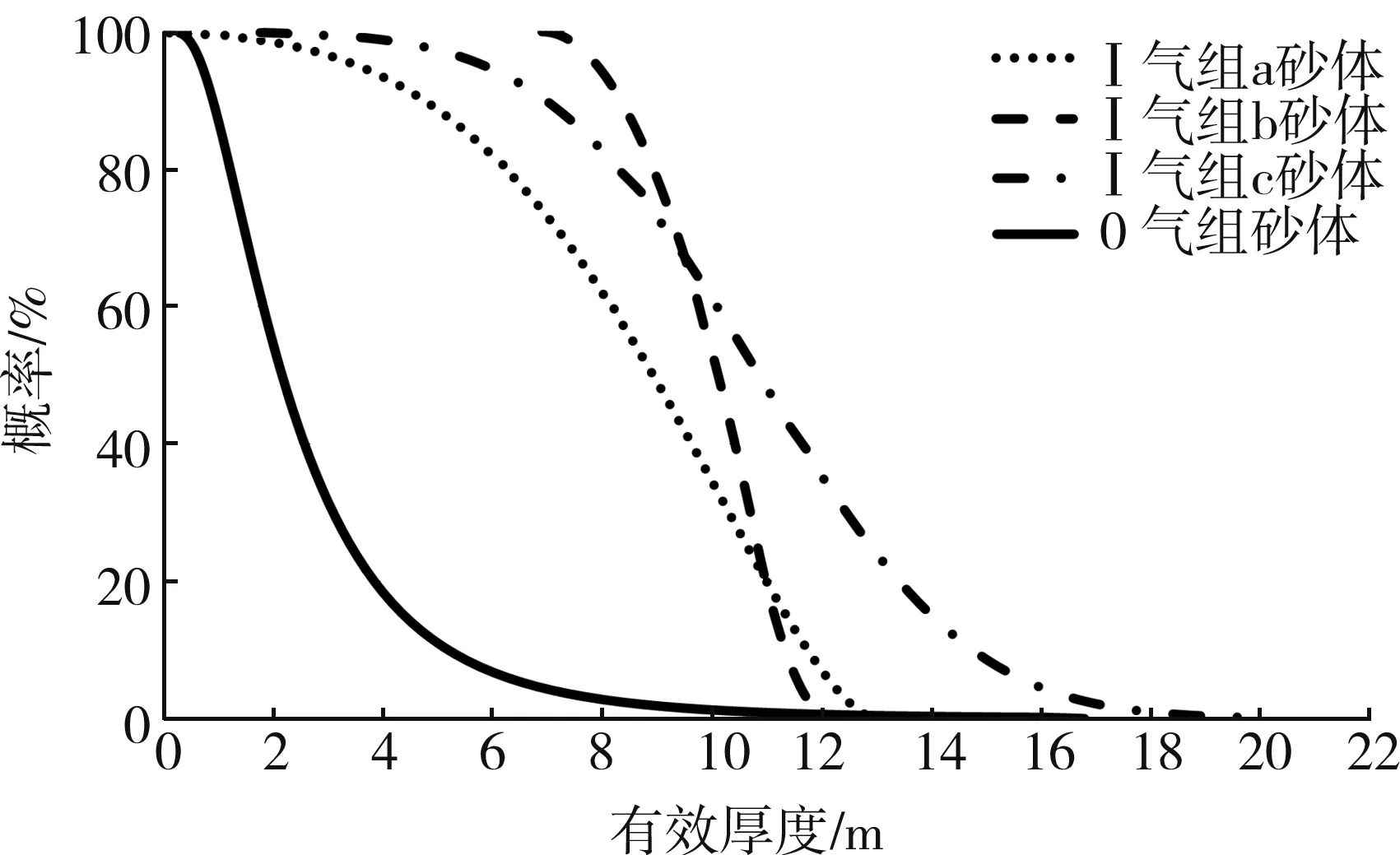
图3 砂体有效厚度贝塔概率分布

图4 气藏油层厚度与形状因子关系图版
应用不同的GRV(岩石毛体积)模型计算岩石总体积,各模型对储量参数类型的输入要求有一定区别。根据已确定的含气面积、有效厚度和形状因子等参数,建立本次GRV概率分布模型:面积+有效厚度+形状因子。图5所示为每套砂体的GRV概率分布模型。

表2 东方A气田4套砂体形状因子统计表
2.4 有效孔隙度及含水饱和度分布函数
有效孔隙度及含水饱和度样本数据取自测井解释结果中的逐点数据,根据气层下限值将无效点剔除。根据样本数据的特点,确定有效孔隙度的对数正态概率分布函数及含水饱和度的正态概率分布函数,从而得到有效孔隙度、含水饱和度概率分布图(见图6、图7)。
3 概率法气藏储量计算应用分析
3.1 储量计算
以I气组a砂体为例计算地质储量,随机模拟次数选择500~30 000次。模拟次数基本上对储量计算结果的影响不大,结果显示4.47×108m3为最佳储量值(见图8)。
按照此方法计算其他3套砂体的地质储量,进而计算出全气田的地质储量。可采用以下两种方法计算全气田的地质储量:(1) 对各计算单元的地质储量进行算术求和;(2) 对各计算单元的地质储量进行单元组合概率求和。
计算结果显示,这两种方法计算出的P50和Pmean储量均相差不大。运用确定性容积法计算的探明地质储量为58.57×108m3,与运用概率法计算出的Pmean储量结果相差不大。表3所示为全气田地质储量对比情况。

图5 各砂体GRV概率分布
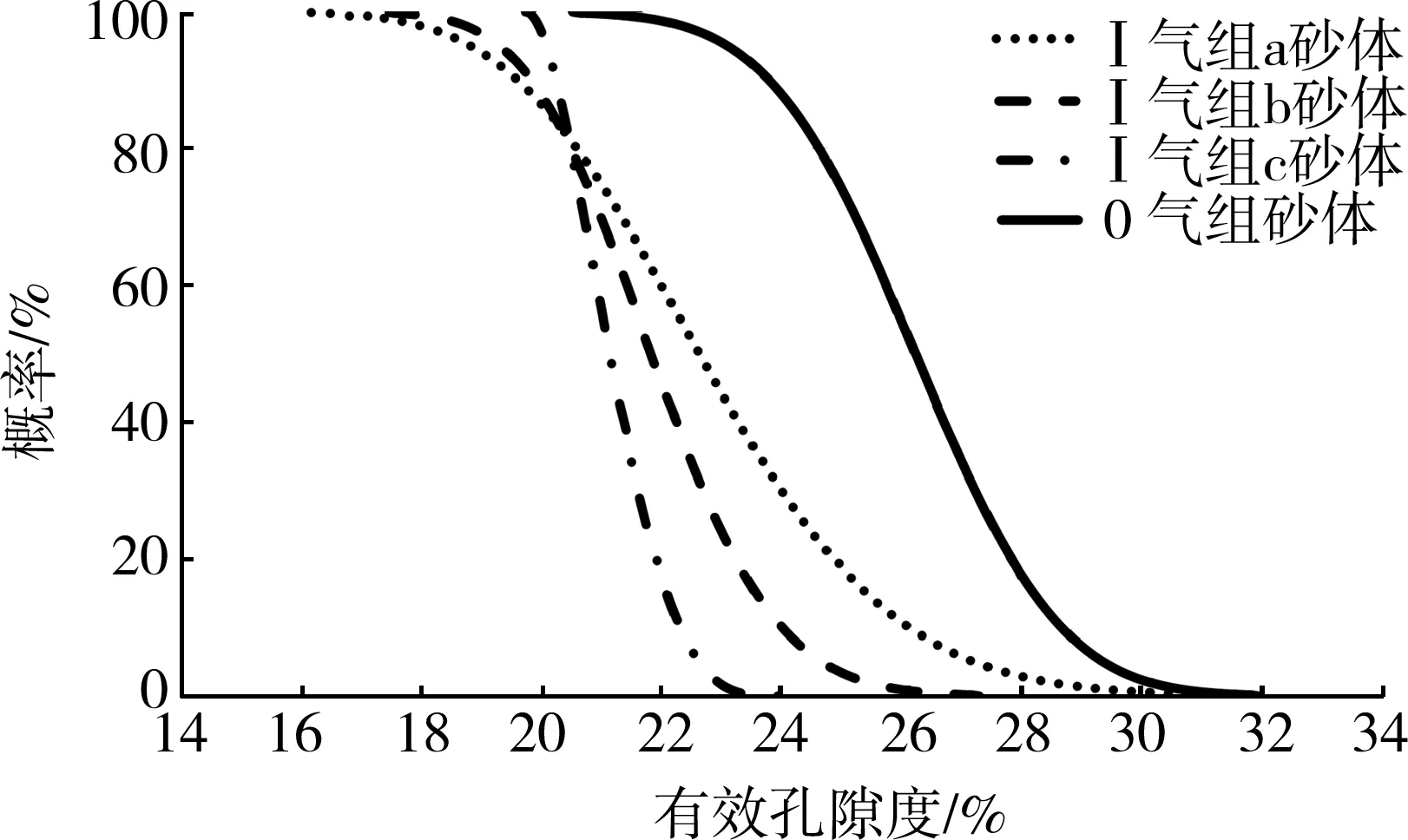
图6 有效孔隙度概率分布

图7 含水饱和度概率分布

图8 I气组a砂体储量概率评估曲线
3.2 储量参数敏感性分析
对计算得到的各套砂体储量计算结果进行储量参数敏感性分析[16]。结果表明,储量的不确定性受含气面积、有效厚度、含气饱和度的影响比较显著(见图9)。
4 结 语
当数据点较少时,储量参数采用三角分布函数或其他最佳拟合分布函数这两种输入方式,对储量评估结果的影响都不大。因此,可采用三角分布函数实现快速评估。

表3 全气田地质储量对比情况 单位:108 m3
分别采用算术求和与组合概率求和的方法计算全气田储量,结果相差不大。相对而言,采用各计算单元算术求和的方法更加简单,因此,可以在快速评估阶段对各计算单元进行算术加和,进而预测整体储量。
