基于日志活动捆绑挖掘隐变迁
2022-01-18胡玉倩方贤文
胡玉倩 方贤文
(安徽理工大学 数学与大数据学院, 安徽 淮南 232001)
流程挖掘是指利用过程挖掘技术将事件数据转化为有价值的可操作知识,主要以流程模型的形式重构业务流程的基础结构。隐变迁是指在模型中能够看到但在日志中看不到的活动,对隐变迁的挖掘有利于增强流程模型的描述性。流程增强是指通过挖掘隐变迁来增强流程模型,从而能够更好地描述流程执行期间得到的事件日志迹集。本次研究将讨论一种通过流程来挖掘隐变迁的方法,该方法主要分为2个阶段:第一阶段,利用事件日志中的高频日志生成初始流程模型;第二阶段,采用松弛的思路,基于高频日志与初始模型行为子集的整体近似适合度及其上下界过滤掉最可能是噪声的低频日志,再利用余下的低频日志来修复模型,最后挖掘出初始模型未曾包含的隐变迁路径。
1 问题的描述
通过流程挖掘得到的流程模型可能会误将有效的低频信息忽略掉,导致日志信息不准确,因此需要对日志进行预处理或对流程模型进行增强。日志预处理中,一般直接对日志进行过滤。模型增强,一般通过日志对模型进行修复。隐变迁的挖掘,实质上就是利用日志活动间的依赖关系将合理的隐变迁挖掘出来,以增强模型的描述性。
传统的挖掘方法,通常是完全将低频日志视为噪声,或者根据挖掘需要去过滤可能存在的噪声。这些传统方法并不能完全适用于所有场景。文献[1]中,将事件标签之间的不频繁直接依赖关系作为不频繁行为的代理,从事件日志构建的自动机中检测并删除这些依赖项,然后通过基于对齐的重放删除单个事件更新原始日志。此方法不能用于处理缺少事件的日志,并且直接删除的只是不频繁行为,而这些不频繁行为不一定都是无效的。文献[2]中,提出了一种新的令牌重放方法,改进了基于令牌重放的操作执行时间,提高了基于令牌重放和对齐的性能,能够管理令牌泛滥的问题。但是,此方法并不能解决活动终止的问题,也不能保证较高的适合度。
2 基本理论
事件日志是过程挖掘的起点。过程模型可描述特定的事件类型,例如保险索赔、客户订单或患者的生命周期等。一个事件可以是一个案例,也可以是一类活动,与特定情况的所有事件序列相对应[3]。

事件日志是迹的多重集,其中可以包含多个具有相同迹的案例。如果迹的频率无关紧要,则将日志引用为一组迹:L={l1,…,ln}。在事件日志的简单定义中,如果一个事件完全通过活动来描述,则无法区分具有相同迹的不同案例。
在本次研究中,系统网使用标签Petri网描述流程,然后将这些概念提升到有标签的变体中[4]。
定义2 (Petri网)一个Petri网(P,T,F)由库所集P,与P不相交的变迁集T,以及一组流弧F⊆(P×T)∪(T×P)组成。系统网N的标识m给每个库所p∈P分配一个托肯自然数m(p)。系统网N=(P,T,F,m0,mf),是一个初始标识为m0、终止标识为mf的Petri网(P,T,F)。
在此,将y的前集和后集分别写作•y:={x|(x,y)∈F}和y•:={x|(y,x)∈F}。 初始标识为[p0],终止标识为[p6]的简单网系统N1,将N1作为运行示例。
Petri网的变迁可以用出自字母表Σ的字母名称来标记,如假设标签τ∈Σ代表一个不可见的动作。标签Petri网(P,T,F,l),是一个标签函数为l:T→Σ的Petri网(P,T,F)。标签网系统N=(P,T,F,l,m0,mf),是一个初始标识为m0、终止标识为mf的标签网(P,T,F,l)。
定义3[4](可行迹)设一个流程模型Petri网为N=(P,T,F,C),发生序列集合为TN,σ=n1,n2,…,nk。若(x,y)⊆(N∪F)×(F∪N),在σ中存在j∈(1,2,…,k-1),j 给定一个系统网SN,φf(SN)是SN的所有完整发生序列的集合,φv(SN)是可见迹的集合,即从其初始标识开始并于其终止标识结束的完整发生序列投影到可见活动的集合(无静默变迁)。 定义4[5](合法移动)设L∈B(A*)是一个事件日志,其中A是活动集,T是模型中的变迁集。此外,设l是返回每个变迁的标签函数。其中ALM是合法移动的集合: ALM={(x,(x,t))|x∈Α∧t∈T∧l(t)=x}∪ {(>>,(x,t))|t∈Τ∧l(t)=x}∪ {(x,>>)|x∈A} 例如,(a,t1)表示日志和模型都产生了一个“a移动”,并且模型中的移动是由变迁t1(因为t1的标签是a的发生造成的,“>>”表明在日志或者模型迹中“无移动”)。定义对齐如下: 使用分配单位成本的标准成本函数δS:如果l(t)≠τ,δS(>>,t)=δS(x,>>)=1。给定日志迹和系统网,其中有可能产生许多对齐记录,为了寻找最优对齐,在此选择总成本最低的对齐。 定义7[5](最优对齐)设L∈B(A*)是一个事件日志,SN是一个φv(SN)≠0的系统网。 Ⅱ 一个对齐γ∈ΓσL,SN,对于迹σL∈L和系统网SN为最优,且对于任意的对齐有γ′∈ΓσL,SN:δ(γ′)≥δ(γ)。 ⅣγSN∈A*→A*是为最优对齐模型迹的可见活动分配任意日志迹σL的一个映射。 定义8(隐变迁)设T′是Petri网业务流程模型中的变迁集,L′是记录日志事件集。l:T′→L′是标签映射,变迁t′称为隐变迁,当且仅当t′∉dom(l),即变迁t′不在l的定义域内。 文献[6]中的Levenshtein距离为常用的距离函数,本次研究用到的编辑距离函数为该距离函数的调整版。 定义9[7](编辑距离函数)设σ,σ′∈A*均为可行迹,编辑距离函数Δ(σ,σ′)→N,返回将σ转换为σ′的最小编辑次数。 进行编辑操作时,允许在迹中删除和插入活动(或变迁标签)。例如,Δ(〈a,c,f,e〉,〈a,f,c,a〉)=4,对应2个删除和2个插入。这个度量具有对称性,即Δ(σ,σ′)=Δ(σ′,σ),其中使用Δ函数而不是标准成本函数。因此,Δ和δS返回相同的距离值。Δ函数按照给定的不同权重插入和删除不同的活动,将单位成本(δS)扩展成另一种成本。 运用式(1),可以将未对齐成本转换为适合度。它通过针对迹中每个活动的一次删除和模型最短路径(SPM)中每个可见变迁的一个插入来规范最优对齐的成本。事件日志L和系统网SN之间的适合度Fitness(L,SN)为迹的加权平均值。 (1) 根据事件日志中不同活动间的绑定关系进行隐变迁挖掘。首先,从完整的事件日志中提取出高频日志,基于高频日志生成初始模型M0;然后,基于行为紧密度来识别有效低频行为的序列;最后,利用有效低频序列中活动间的绑定关系,挖掘行为模型中的隐变迁。 事件日志由迹的多重集构成,活动集的集合为事件日志,各种活动间的行为关系一般由行为轮廓来描述。在此,基于捆绑的概念简单描述日志中各活动间的行为关系:捆绑由六元组(A,ai,ao,D,I,O)组成,其中A为一个有限的活动集,ai∈A表示开始活动,ao∈A表示结束活动;D⊆A×A表示依赖关系,而AS={X⊆P(A)|X={φ}∨φ∉X};I∈A→AS为输入捆绑活动集,O∈A→AS为输出捆绑活动集,DI∈A→AS为直接输入捆绑活动,DO∈A→AS为直接输出捆绑活动,则有: {ai}={a∈A|(a)={φ}} {ao}={a∈A|O(a)={φ}} 对于日志〈a,b,c,e〉、〈a,c,e〉和〈a,b,e〉可得到活动c,其直接输入捆绑活动集为Ic={a,b},直接输出捆绑活动集为Oc={e}。 根据日志活动间捆绑的定义,可以得到每个活动的输入捆绑活动集、输出捆绑活动集,开始或结束活动。同时,根据有效低频信息中的多条日志得到活动的输入、输出捆绑活动集,发现模型的不直接相连活动,从而挖掘出模型中的隐变迁,完成流程模型的修复。 在此,根据日志与初始模型的行为子集MB⊆φv(SN)的近似适合度及其区间值确认有效低频和噪音。当日志与MB的近似适合度值未超出区间范围时,该低频日志被认定为有效低频;否则,该低频日志被认定为噪声。使用编辑距离函数Δ,获得对齐成本的上界,即适合度的下界。 引理1(对齐成本上界)。设σL∈A*是一个日志迹,σM∈φv(SN)是SN的课件发生序列,则有δS(γSN(σL))≤Δ(σL,σM),其中γSN(σL)为最优对齐[7]。 3.2.1 构建模型行为子集 使用MB,即可见模型迹的子集,以获得近似的适合度值。采用候选选择的方法构建MB,主要步骤如下[7]: (1) 在事件日志L中任意选择2条迹(即候选者)放入LC。按照松弛的思想,应选择高频迹中频次较低的迹。在表1所示日志中,越符合流程模型的迹,其产生的可能性就越高。若是考虑频次最高的2条迹〈a,b,c,e,f〉和〈a,b,d,e,f〉,产生的适合度甚至会高达1,这样便达不到松弛的目的;若是选择频次最低的2条迹,则最低频的迹最可能为噪声。故,可选择〈a,b,d,e,f〉和〈a,c,e,f〉。 (2) 对于每个σL∈LC,找到最优对齐并将λSN(σL)插入到MB。对照表1所示日志,分别将〈a,b,d,e,f〉和〈a,c,e,f〉置于初始模型中重放,即可得到与模型对齐的最优对齐所对应的模型迹,组成行为子集(MB)。 表1 示例日志 3.2.2 计算近似适合度 (3) 对于高频部分,根据加权平均法得到高频日志迹与初始模型总体的近似适合度ΦAF总,以及总体上下界[ΦLP,ΦUP]。 通过上述步骤得到每条日志迹与模型迹,以及高频日志迹与初始模型整体的近似适合度ΦAF总及其上下界[ΦLP,ΦUP]。比较低频日志迹的近似适合度值ΦAF与[ΦLP,ΦUP]:若ΦAF⊂[ΦLP,ΦUP],则该日志迹为松弛后的有效低频日志迹,可用于修复初始模型;若ΦAF⊄[ΦLP,ΦUP],则该日志迹为噪声。据此得到的有效低频日志迹即松弛后的日志迹,利用这些日志迹活动的直接输入和输出捆绑活动集即可挖掘隐变迁,并添加合理的发生路径。 挖掘初始模型中缺少的隐变迁,进而修复模型。 (1) 日志迹。列出日志迹中所有活动的直接输入和输出捆绑活动集。 (2) 初始模型。根据Petri网前集与后集概念列出每个变迁的直接输入前集与直接输出后集。 比较日志迹与初始模型的挖掘结果,若松弛得到的有效低频日志迹中活动集与该活动在模型中变迁所得直接前集中的元素不同,则可以确定其中存在合理的隐变迁。在其他情况下,皆无须添加合理路径。 医院日常活动通常产生庞大的流水日志。其中有些相对低频的日志不完全与高频日志挖掘到的模型相符,但是却属于正确流程。这些日志在大多流程挖掘过程中都被视为噪声而过滤掉,或者直接被认为是正确的日志而用于挖掘。当这些日志被滤掉时,会使模型缺失极少发生的一部分正确流程;而当这些日志全部被视为正确流程时,又会使模型复杂化,影响其精度。 在此,以某精神病院家属接病人出院时的行为日志为例(见表2 )进行挖掘分析。基于该日志的前5种高频迹,生成初始模型N1。虽然N1可以代表出院的正确流程,然而并不能解释某些特殊情况下未完成路径或已完成特殊路径的正确出院流程。例如,申请人在确认费用时,出现了不能及时支付的情况。 表3所示为医院病人出院活动名称。 表2 示例日志 表3 医院病人出院活动名称 根据上述事件日志,应用挖掘算法得到图1所示Petri网初始模型N1,该模型符合精神病院患者家属申请出院的一般流程。 图1 Petri网初始模型N1 图1中的活动发生路径基本涵盖了办理出院的一系列流程,然而对于一些特殊情况并未描述出来。有些低频日志实际上对流程的完善是有益的,利用这些有用的低频日志来挖掘隐变迁,可以改善模型的合理发生路径。 选择所有可能日志迹中相对低频的部分,可以降低适合度的下界,从而达到松弛的目的,故将 〈a,b,d,e,f,g,h〉和〈a,b,d,e,f,h〉放入LC,然后将这2条迹放入初始模型N1中进行重放。可以看出迹本身即为其相应的最优对齐的模型迹,针对表2构造的模型行为子集为: MB={〈a,b,d,e,f,g,h〉,〈a,b,d,e,f,h〉} 利用表2中日志与MB计算近似适合度,结果见表4。 表4 模型适合度计算数据 根据表4所示数据,去掉4种低频迹,得到模型的松弛近似适合度为0.801,适合度的下界、上界分别为0.786、1.000,因此,日志与模型的适合度区间为[0.786,1.000]。运用此方法计算出剩余3条低频迹的近似适合度,其值分别为0.818、0.800、0.769。前两条迹的近似适合度值落在区间范围内,可知迹〈a,c,e,f,g,h〉、〈a,b,e,f,g,h〉和〈a,b,d,e〉为有效低频迹,迹〈a,h〉为噪声。接着,可利用迹中活动的输入输出捆绑活动集挖掘初始模型中被忽略的隐变迁。 对于迹〈a,c,e,f,g,h〉、〈a,b,e,f,g,h〉和〈a,b,d,e〉,列出其活动的输入输出捆绑集(见表5)。为了使对比更明显,列出初始模型N1中变迁的直接前集与后集(见表6)。 表5 输入输出捆绑活动集 表6 N1的直接前集与后集 由表5和表6可以看出,事件日志中活动e的输入输出捆绑活动集分别为{a,b,d}和{f}∪{φ},而N1中变迁e的直接前集和后集分别为{c,d}和{f}。由此可推断出,变迁a与变迁e之间、变迁b与变迁e之间各自有一个隐变迁,变迁e与终止标识p7之间应该也存在一个隐变迁。其他剩余活动的输入与输出捆绑活动集均处于N1的变迁直接前集与后集的集合内。最终得到的模型为N2,如图2所示。 图2 挖掘隐变迁后的模型N2 现有的挖掘方法大多默认事件日志完全无噪声,或者将所有可能的低频日志都视为噪声,这是与事实不符的。本次研究提出的增强挖掘流程方法,主要挖掘流程中的隐变迁分支,以增强模型的适合度。同时,提出了日志中活动的输入捆绑及输出捆绑的概念,用于识别存在于日志中而流程模型中没有的活动捆绑关系来确定隐变迁的存在位置,增强了模型的描述性与适用性。其次,运用松弛思想,在选择低频日志中的有效低频时,过滤掉最可能是噪声的低频日志。最后,利用剩余低频近似适合度与初始模型行为子集适合度上下界区间范围对初始模型进行修复。基于松弛思想,所得模型更符合日志的实际情况。



3 隐变迁的挖掘
3.1 事件日志活动间的捆绑集
3.2 噪声与有效低频的松弛区分

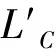

3.3 利用直接输入和输出捆绑活动集挖掘隐变迁
4 实际案例分析







5 结 语
