重心插值配点法求解Cahn-Hilliard方程
2022-01-18邓杨芳黄蓉翁智峰
邓杨芳, 黄蓉, 翁智峰
(华侨大学 数学科学学院, 福建 泉州 362021)
1958年,Cahn等[1]在研究热力学两相物质(如合金、聚合物等)之间的相互扩散现象时,提出Cahn-Hilliard方程.Cahn-Hilliard方程是一类重要的四阶非线性扩散方程,用来描述固体表面上微滴的扩散、河床的迁移、生物种群的竞争与排斥等扩散现象,也广泛应用于工程流体力学[2-3]、材料科学[4]、图像分析[5-6]和生命科学[7-8]等领域.国内外学者对Cahn-Hilliard方程提出了许多数值解法,如有限差分[9-11]、有限元[12-13]、有限体积[14]、谱方法[15-16]等.Zhang等[17]构造一个无条件能量稳定的有限差分格式,并基于该格式提出自适应时间步长策略.Cheng等[18]采用快速稳定的显式算子分裂方法求解Cahn-Hilliard方程.Li等[19]考虑求解二维Cahn-Hilliard方程的半隐稳定化傅里叶谱方法,并对几种经典的稳定化技术进行比较研究,确定相应的稳定区域.Cheng等[20]提出一个能量稳定的四阶差分格式求解带周期边界条件的Cahn-Hilliard方程,并证明该格式解的唯一性和能量稳定性.Wang 等[21]提出一个能量稳定的线性扩散Crank-Nicolson格式求解Cahn-Hilliard方程.Zhang等[22]构造一类无条件能量稳定的线性二阶预估-校正时间步进格式求解Cahn-Hilliard方程.
上述方法都是基于网格剖分求解微分方程问题.李淑萍等[23]利用重心插值配点法求解微分方程初边值问题,重心插值配点法包括重心Lagrange插值和重心有理插值.对于等距插值节点,高阶Lagrange插值公式构造的近似函数值容易出现Runge现象,具有极大的数值不稳定性.为了避免这一现象的出现,Berrut等[24]分别将Lagrange插值公式改为重心Lagrange插值和重心有理插值[25],克服数值格式的振荡现象.重心插值配点法作为一种新型的无网格计算方法,具有计算格式简单、精度高、程序实施方便、节点适应性好等特点,使用Chebyshev节点有效克服了Runge现象.重心插值配点法被推广到求解各类积分和微分方程,如高维Fredholm积分方程[26]、非线性抛物方程[27]、粘弹性波方程[28]、Allen-Cahn方程[29-30]、Black-Scholes方程[31]等.本文将重心插值配点法推广到求解Cahn-Hilliard方程.
1 Cahn-Hilliard方程的重心插值配点法
1.1 Cahn-Hilliard方程
Cahn-Hilliard方程是相场模型方程之一,用来模拟二元合金中的相分离现象,即
φt(x,t)=Δ(F′(φ(x,t))-ε2Δφ(x,t)),x∈[a,b],t∈[0,T].
(1)
边界条件为
φ(a,t)=α1(t),φ(b,t)=α2(t),φ′(a,t)=β1(t),φ′(b,t)=β2(t).t∈[0,T],
(2)
初始条件为
φ(x,0)=ψ(x),x∈[a,b].
(3)
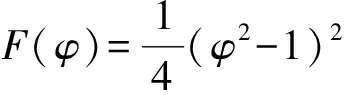
Cahn-Hilliard方程也可看作是H-1内积下的一个梯度流,它的自由能泛函为
(4)
式(4)中:∇是梯度算子.
令μ=F′(φ)-ε2Δφ,方程(1)与μ作内积可得

(5)
因此,Cahn-Hilliard方程满足能量递减规律,在采用数值方法求解Cahn-Hilliard方程时,不仅要保证数值精度,而且要保证能量的稳定性.
1.2 重心型插值
1.2.1 重心Lagrange插值 设有插值节点tj和一组对应的实数fj(j=0,1,…,m),采用多项式插值,则在次数不超过m的多项式空间可以找到唯一的插值多项式p(t),满足p(tj)=fj,j=0,1,…,m,Lagrange插值公式为
(6)
(7)
(8)

(9)
将式(9)代入式(6),有
(10)
由式(8)~(10),可得重心Lagrange 插值公式,即
(11)
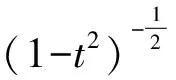
1.2.2 重心有理插值 设有插值节点tj(j=0,1,…,m)和一组对应的实数fj,选择一个整数d且满足0≤d≤m,令pj(t)为插值d+1个点对(tj,fj),(tj+1,fj+1),…,(tj+d,fj+d)(j=0,1,…,m-d)的次数最多为d的多项式,则
(12)
式(12)中:λj(t)=(-1)j/((t-tj)…(t-tj+d)).
将pj(t)写成Lagrange插值形式,整理得
(13)
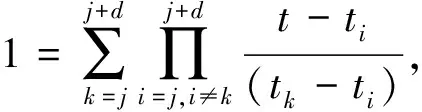
(14)
将式(13),(14)代入式(12),得到高阶重心有理插值公式,即
(15)
重心有理插值基于混合函数的思想,可以有效克服等距插值的不稳定问题.
1.2.3 重心插值的微分矩阵 由式(15),函数r(t)在节点t0,t1,…,tm处的v阶导数为
(16)
由文献[32],一阶和二阶微分矩阵的计算公式为
(17)
利用数学归纳法,可以得到v阶微分矩阵的递推公式
(18)
1.3 一般迭代格式下的Cahn-Hilliard方程
(19)
式(19)中:k为迭代次数.
1.4 Cahn-Hilliard方程的重心插值配点格式
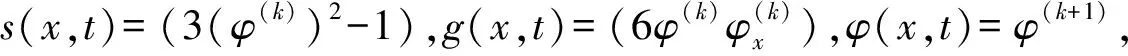
φt+ε2φxxxx-s(x,t)φxx-g(x,t)φx=0.
(20)
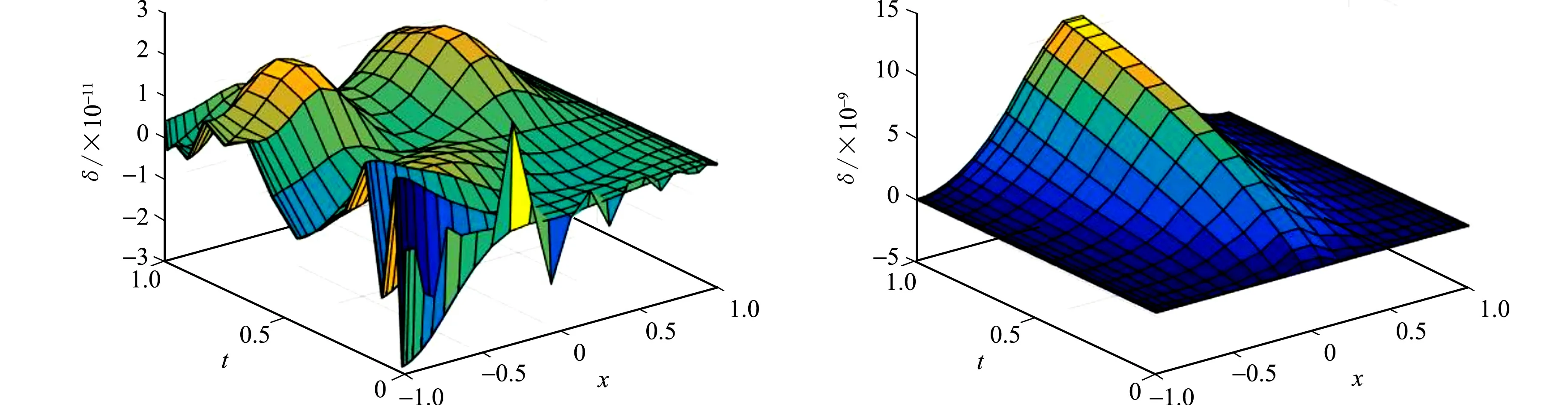
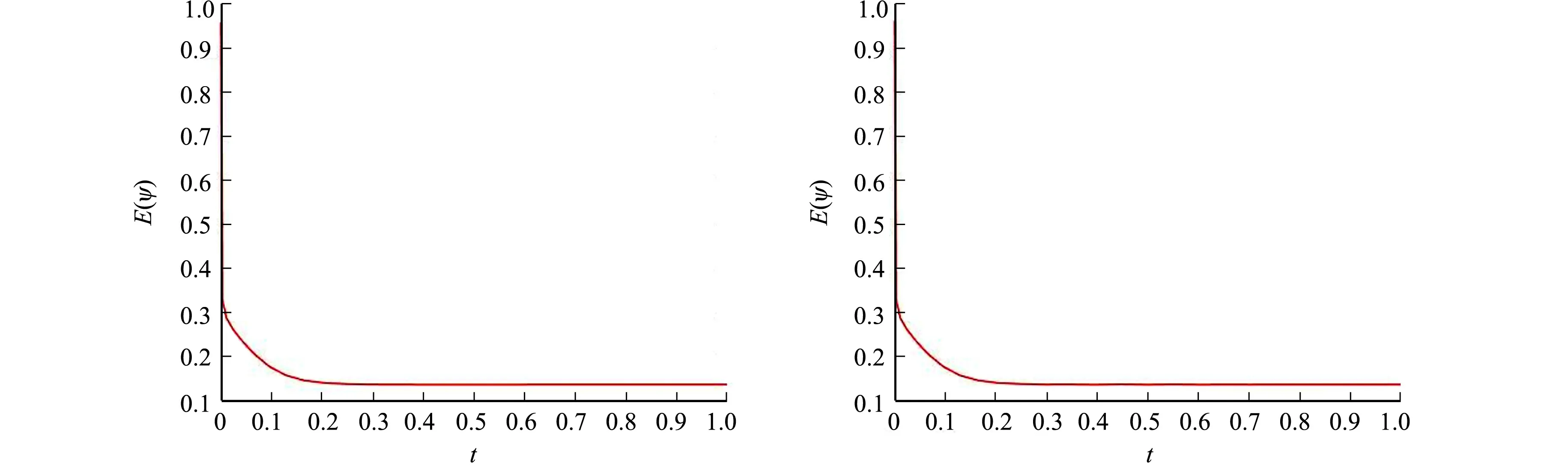
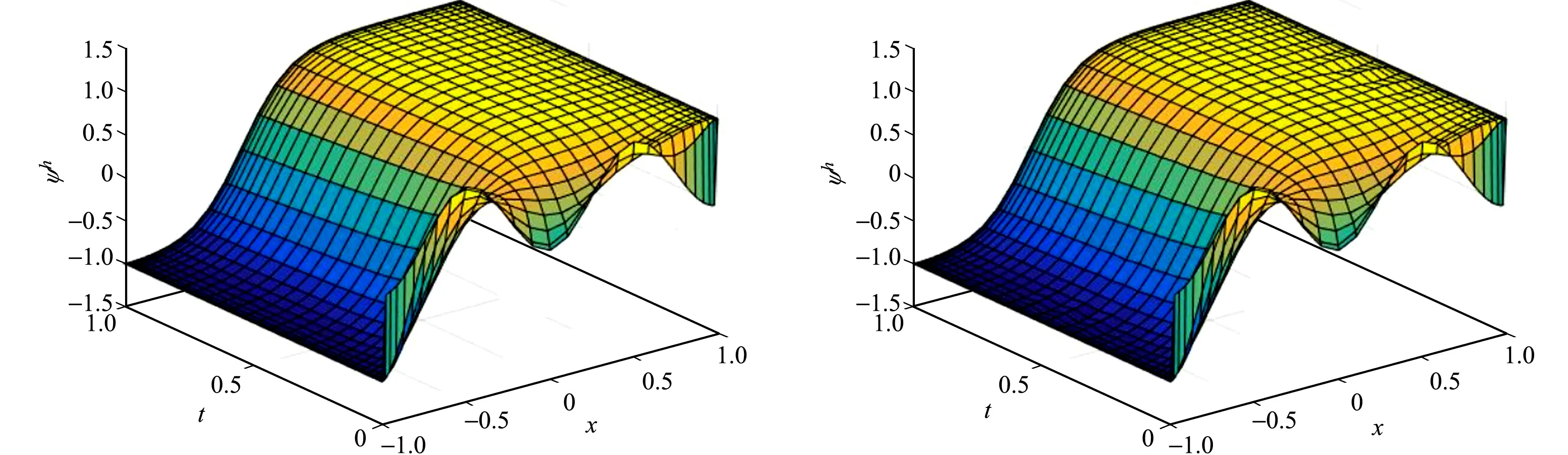
首先,对空间域[a,b]和时间域[0,T]进行网格剖分:a=x0 (21) 将式(21)代入式(20),使其在点x0,x1,…,xM上成立,有 (22) (23) 记φi(tj)=φ(xi,tj):=φi,j,得到φi(t)在点t0,t1,…,tN上的重心插值函数,即 (24) 将式(24)代入式(23),使其在点t0,t1,…,tN上成立,有 (25) φi=[φi,0,φi,1,…,φi,N]T, si=diag(si,0,si,1,…,si,N)=diag(si(t0),si(t1),…,si(tN)), gi=diag(gi,0,gi,1,…,gi,N)=diag(gi(t0),gi(t1),…,gi(tN)),i=0,1,…,M. 方程(25)可以简记为矩阵形式,即 (26) 式(26)中:符号⊗代表矩阵的Kronecker积;IM,IN分别为M+1,N+1阶单位矩阵;C(v),D(v)(v=1,2,3,4)分别表示节点x0,x1,…,xM和t0,t1,…,tN上的重心插值v阶微分矩阵.设 则式(26)可以表示为 [(IM⊗D(1))+ε2(C(4)⊗IN)-s(C(2)⊗IN)-g(C(1)⊗IN)]φ=0. (27) 类似地,采用重心插值格式逼近s(x,t)和g(x,t),得到Cahn-Hilliard方程在重心插值配点法下的迭代计算格式,即 [IM⊗D(1)+ε2(C(4)⊗IN)-diag(3(φ(k))2-1)(C(2)⊗IN)- (28) 由插值逼近误差理论估计最后的误差范围,有助于检验算法在计算过程中的整体误差结果.由文献[33]的定理3.1,得到定理1. 定理1如果φ(x,t)∈Cn+1(Ω),Ω=[a,b]×(0,T]∈R2是一个带Lipschitz连续边界的非空开集,φh(x,t)为φ(x,t)的重心Lagrange插值函数,则有如下误差估计成立,即 (29) (30) (31) 证明:设xi(i=0,1,…M)为区间[-1,1]上的Chebyshev节点,x0=1,xM=-1,φ(x)∈Cm+1(-1,1),由文献 [33],有 (32) 由拉格朗日插值余项定理,有 (33) 式(33)中:v表示求导的次数,v=1,2,3,4. 当M≫1时,由Stirling公式知 (34) 结合式(32)~(34),有 2.2.4 聚3-吲哚基环氧丙烷(Poly-IDPOs)、聚3-咔唑基环氧丙烷(Poly-CDPOs) (35) (36) 式(36)中:当n较大时,c0,c1是与M无关的常数. (37) (38) 对于二元函数φ(x,t),有 |φ(x,t)-φh(xm,t)+φh(xm,t)-φh(xm,tn)|≤|φ(x,t)-φh(xm,t)|+|φh(xm,t)-φh(xm,tn)|≤ (39) 即有式(29)成立.取v=4,由式(38)即可得到式(30),同理可得式(31). 从逼近误差结果可知,该算法是指数收敛的,且微分算子的阶数决定了代数方程的收敛阶. 给出两个数值算例来验证重心插值配点格式的高精度和有效性.记uh,u分别为数值解和真解向量,定义相对误差和绝对误差分别为 (40) 式(40)中:‖·‖∞表示无穷范数. 为对比两种重心插值配点格式的精度,选取三角函数精确解的方程作为测试实例.考虑Cahn-Hilliard方程,即 (41) 当ε=0.3时,求解问题(41),重心Lagrange插值配点格式和重心有理插值配点格式的误差比较,如表1所示.由表1可知:节点数量在一定范围内增加时,两种重心插值配点格式的计算误差与节点数量之间呈指数下降,取较少节点数时,如M=20,25,N=10,10,重心Lagrange插值配点格式的精度高于重心有理插值配点格式的精度;随着计算节点的进一步增加,两种重心插值配点格式的绝对误差Ea和相对误差Er都出现微小振荡,重心有理插值配点的表现更平稳,但仍都维持在10-11和10-10量级;两种重心插值配点格式都具有很高的计算精度和较好的数值稳定性;综合比较可知,重心Lagrange插值配点格式的精度更高,重心有理插值配点格式的数值稳定性更好. 表1 两种重心插值配点格式的误差比较Tab.1 Error comparison of two barycentric interpolation collocation formats 取M=25,N=15,重心Lagrange插值配点格式和重心有理插值配点格式的数值解图及误差分布图,分别如图1,2所示.图1,2中:φh为数值解,δ为数值解和真解之间的误差. (a) 重心Lagrange插值配点 (b) 重心有理插值配点 图1 两种重心插值配点格式的数值解图(M=25,N=15)Fig.1 Numerical solution graph of two barycentric interpolation collocation formats (M=25,N=15) (a) 重心Lagrange插值配点 (b) 重心有理插值配点 图2 两种重心插值配点格式的误差分布图(M=25,N=15)Fig.2 Error distribution diagram of two barycentric interpolation collocation point formats (M=25,N=15) 由图1,2可知:两种重心插值配点格式的数值图像几乎一致,均逼近于真实解,但重心Lagrange插值配点格式的精度更高. 为了进一步验证数值格式的有效性,考虑 Cahn-Hilliard方程的离散能量函数,即 (42) φ(-1,t)=-1,φ(1,t)=1,φ′(-1,t)=φ′(1,t)=0. 取M=30,N=30,在不同ε2取值下,两种重心插值配点格式求解Cahn-Hilliard方程对应的能量递减图及数值解图,分别如图3,4所示. (a) 重心Lagrange插值配点(ε2=0.09) (b) 重心有理插值配点(ε2=0.09) (c) 重心Lagrange插值配点(ε2=0.04) (d) 重心有理插值配点(ε2=0.04)图3 不同ε2取值下两种重心插值配点格式的能量递减图(M=30,N=30)Fig.3 Energy declining graphs of two barycentric interpolation collocation point formats under different values of ε2 (M=30, N=30) (a) 重心Lagrange插值配点(ε2=0.09) (b) 重心有理插值配点(ε2=0.09) (c) 重心Lagrange插值配点(ε2=0.04) (d) 重心有理插值配点(ε2=0.04) 图4 不同ε2取值下两种重心插值配点格式的数值解图(M=30,N=30)Fig.4 Numerical solution graph of two barycentric interpolation collocation schemes under different ε2 values (M=30, N=30) 由图3可知:两种重心插值配点格式均满足能量递减规律,即随着时间t递增,能量函数E(φ)不断递减,最后达到稳定状态;当ε2变小时,趋于稳定状态的时间会变长,能量值会变小.由图4可知:不管ε2取何值,重心Lagrange插值配点插值效果都更好,数值解图像更光滑,两种重心插值配点格式图像最终都趋于稳态. 利用重心Lagrange插值配点格式和重心有理插值配点的一般迭代格式求解Cahn-Hilliard方程,并给出了重心lagrange插值的逼近误差.数值算例比较了两种重心插值配点格式的精度和稳定性.当剖分节点数较少时,重心lagrange插值精度更高;当剖分节点数较多时,重心有理插值配点稳定性更好.最后,验证了两种格式均满足能量递减规律.接下来将进一步研究重心插值配点推广到高阶非线性的问题.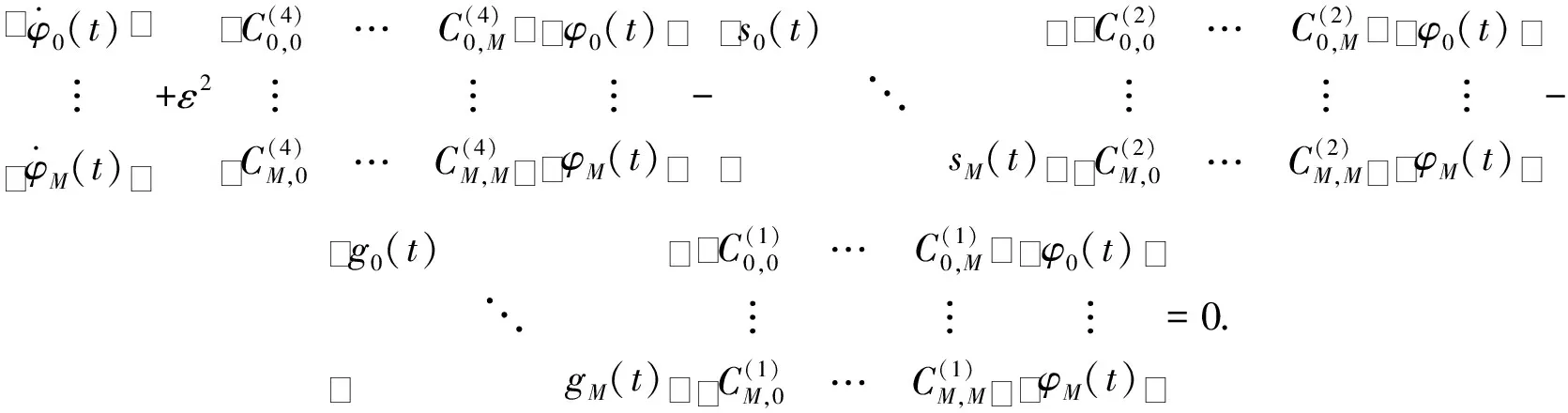

diag(6φ(k)((C(1)⊗IN)φ(k)))(C(1)⊗IN)]φ(k+1)=0.1.5 插值误差估计

2 数值算例
2.1 算例1


2.2 算例2

3 结束语
