地下水对地埋管换热器换热的影响分析
2022-01-18李泽锟杜震宇
李泽锟, 杜震宇
(太原理工大学 土木工程学院, 山西 太原 030024)
随着建筑能耗的增加和环境问题的日益严峻,开发和利用可再生能源受到越来越多的关注[1].土壤源热泵因充分利用浅层地热、稳定性高、地上空间占用较小等优点受到越来越多的关注.地埋管换热器作为土壤源热泵的核心组成部分,其换热能力受周围岩土体的热物性和地下水的影响较大.为了分析地埋管换热器的换热量和周围岩土体的温度变化,国内外学者构建了许多地埋管换热器的传热模型.黄雪婷[2]通过分层渗流模型,研究地下水位线高度和地下水流速对地埋管换热器换热的影响.Abdelaziz等[3]根据有限长线热源模型,得到岩土体内任意一点的温度响应,并根据各层的导热系数得到分层换热量的经验公式.文献[4-5]通过有限长线热源模型和移动线热源模型,建立岩土体分层渗流解析模型.Selçuk等[6]对文献[3]的模型进行优化,并考虑渗流的作用.李永等[7]通过热物性测试实验的数据,建立三维分层岩土体模型,并考虑了岩土体的初始温度.张山等[8]建立三维非稳态传热模型,分析地下水渗流、流速和含水层厚度对地埋管换热器周围岩土体温度场和换热量的影响.文献[9-10]建立三维数值模型,将含水层处的导热系数等效为无渗流的导热系数,并研究含水层厚度对热物性检测的影响.
目前,关于地下水对地埋管换热器换热的研究还相对较少.因此,本文建立地埋管换热器的三维非稳态分层渗流传热模型,分析含水层厚度、地下水流速和岩土体孔隙率对地埋管换热器换热的影响.
1 传热模型的建立
1.1 模型的假设
地埋管换热器的换热过程是复杂的非稳态换热,需对模型进行简化,有以下5个假设.1) 对计算区域的岩土体进行分层,各层岩土体视为均质介质,且岩土体热物性不随时间和空间而变化.2) 假设循环流体、地埋管换热器、回填材料和岩土体间不存在接触热阻.3) 假设地下水渗流仅存在于水平方向,且速度恒定.4) 假设固体和液体在接触的瞬间达到热平衡状态.5) 忽略地埋管换热器底部弯管的影响.
1.2 几何模型
将某项目土壤源热泵系统作为建立竖直地埋管换热器传热模型的基础[11],该项目处于典型的黄土高原地区,根据该地区的地质条件,沿轴向将岩土体分为5层,自上而下分别为湿陷性黄土、黄土、卵石、强风化砂岩和中风化砂岩.该项目采用单U型地埋管换热器,管内换热介质为水,回填材料为砂土,U型管为聚乙烯(PE)管,传热模型的热物性参数,如表1所示.表1中:ρ为密度;α为热扩散系数;λ为导热系数;φ为孔隙率;K为渗透率.
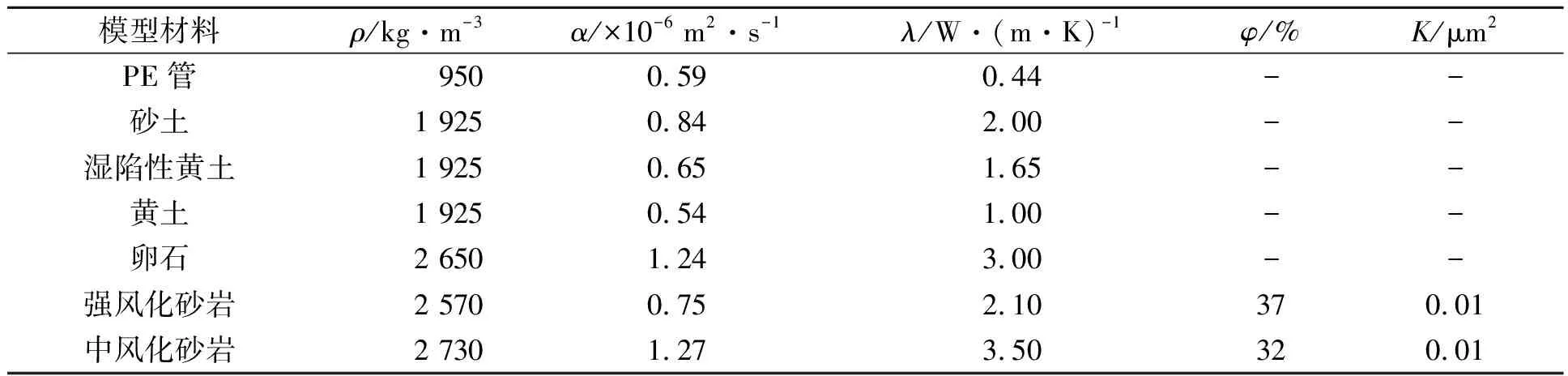
表1 传热模型的热物性参数Tab.1 Thermal physical property parameters of heat transfer model
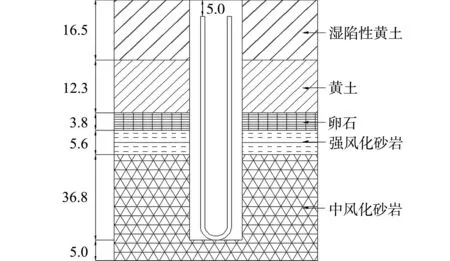
图1 地埋管换热器及岩土体模型图(单位:m)Fig.1 Model of ground heat exchanger and rock-soil body (unit: m)
为了防止边界对模拟的干扰,将计算区域设置为6 m×6 m×80 m(长×宽×高)的六面体岩土体,钻井(圆柱体)设置于计算区域的几何中心,其埋深为75 m.地埋管换热器及岩土体模型图,如图1所示.
钻井与钻井内部的相关参数,如表2所示.表2中:d为钻井直径;b0为支管间距;d1为U型管外径;d2为U型管内径;L为地埋管换热器的埋深.
通过Fluent流体仿真软件,建立地埋管换热器的三维非稳态分层渗流传热模型.对几何模型进行网格划分,由于计算区域的温度轴向变化相对较小,故竖直方向的网格相对稀疏,而水平方向的网格则需进行加密处理.忽略底部弯管的影响,将U型管简化为1根进水管和1根出水管,通过用户自定义函数(UDF),将进水支管与回水支管的底部相连接.

表2 钻井与钻井内部的相关参数Tab.2 Related parameters of borehole and borehole internal (mm)
1.3 数学模型
1.3.1 多孔介质的控制方程 多孔介质的质量守恒方程为

(1)
式(1)中:ρs,w为多孔介质中流体密度;u为多孔介质中流体流速;Q为控制体内热源的强度;t为时间.
多孔介质的动量守恒方程为
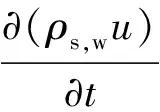
(2)
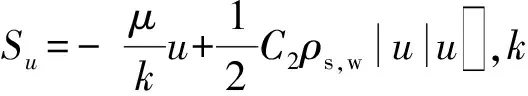
多孔介质的能量守恒方程为
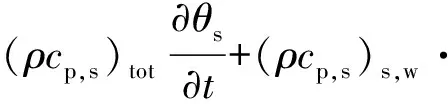
(3)
式(3)中:cp,s为多空介质中固体的体积比热容;θs为岩土体温度;(ρcp,s)tot为多孔介质总的体积比热容,(ρcp,s)tot=φ(ρcp,s)s,w+(1-φ)(ρcp,s)s;λtot为多孔介质总的导热系数,λtot=φλs,w+(1-φ)λs,λs,w,λs分别为多孔介质中流体和固体的导热系数.
1.3.2 管内循环流体的控制方程 管内循环流体的质量守恒方程为

(4)
式(4)中:ρw为管内流体的密度,当流体为不可压缩流体时,密度为定值;U为管内流体的流速.
管内循环流体的动量守恒方程为
(5)
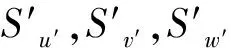
管内循环流体的能量守恒方程为
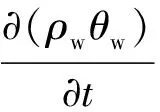
(6)
式(6)中:θw,λw,cp,w分别为管内流体的温度、导热系数和体积比热容;Sθw为该方程的源项.
1.3.3 数值计算方法 采用Realizablek-ε双方程湍流模型,通过压力隐式算子分割(PISO)算法对状态方程进行求解.离散格式为二阶迎风格式.进行非稳态计算时,时间步长设置为60 s,收敛条件的能量残差设置为1×10-8,其余残差设置为1×10-6.
1.4 定解条件
1.4.1 初始条件 将岩土体设置为多孔介质,岩土体周围的边界设置为恒温边界,其温度分布与岩土体初始温度分布相同.进行地埋管换热器的模拟计算时,岩土体初始温度对结果影响较大[12],故需考虑岩土体轴向的初始温度变化.经实际测量,岩土体并未出现明显的恒温层.深度为0~20 m的岩土体温度受外界温度的影响较大,深度为20 m以下的岩土体温度因地热作用随深度的增加而升高.考虑地热作用,对实测数据进行拟合,可得岩土体初始温度轴向变化的公式为
θs,0=-0.012z+11.04, 0≤z≤20,
(7)
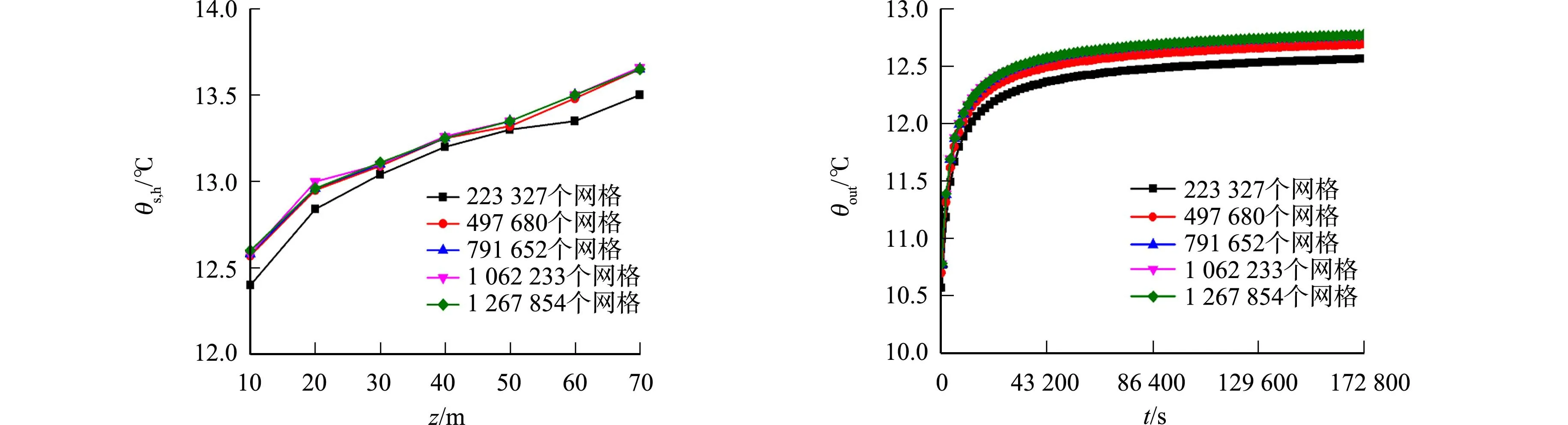
θs,0=0.016z+10.46, 20 (8) 式(7),(8)中:θs,0为岩土体初始温度,℃;z为岩土体的深度,m. 1.4.2 边界条件 当埋深为0.005,0.045 m时,地埋管换热器换热受太阳辐射的影响较大;当埋深为0.300 m以下时,地埋管换热器换热几乎未受太阳辐射的影响[13].由于文中地埋管换热器的埋深为70 m,地埋管换热器的顶端距离地面为5 m,因此,可忽略太阳辐射的影响,仅考虑外界空气温度变化对地埋管换热器换热的影响.将计算区域顶部设置为第3类边界条件,其中,流体温度设定为夏季典型日随时间变化的空气温度,则外界空气温度θup为 (9) 利用季节平均温度,经计算,可得地面与周围空气的对流换热系数为0.48 W·(m·K)-1.在含水层设置一定流速的地下水渗流,地下水温度与岩土体初始温度相同.U型管入口设置为速度入口,出口设置为压力出口. 作为数值解的网格应足够细密,使进一步加密网格对数值解几乎没有影响.这种数值解称为网格独立的解[14].对网格数量分别为223 327,497 680,791 652,1 062 233,1 267 854的模型进行模拟,设置进口温度为14 ℃,进口流速为0.23 m·s-1. 待岩土体的温度场稳定后,进行网格独立性检验,其结果如图2所示.图2中:θs,h为回水侧岩土体轴向温度;θout为出水温度.由图2可知:当网格数量不低于497 680时,回水侧岩土体轴向温度分布基本不变.综合考虑计算效率和模型的精确度,选择497 680个网格的模型. (a) 回水侧岩土体轴向温度 (b) 出水温度 图2 网格独立性检验Fig.2 Grid independence verification 单位井深换热量是衡量地埋管换热器换热能力的参数,表达式为 (10) 根据文献[15],分层单位井深换热量可直观地反映各层岩土体的换热能力,表达式为 (11) 式(11)中:qi为第i层岩土体的单位井深换热量,W·m-1;θin,i,θout,i分别为第i层岩土体顶面的进水温度和出水温度,℃;Li为第i层岩土体的厚度,m. 为了更加简单、有效地观察各层岩土体的换热量占总换热量的份额,确定最优的埋深,提出分层单位井深换热比率,即 (12) 式(12)中:Ni为第i层的分层单位井深换热比率. 地下水对第i层岩土体位置处地埋管换热器换热的影响可通过该层单位井深换热量增加率进行表示,即 (13) 为了验证模型的准确性,选取文献[11]中2011年7月24日在不同埋深的供、回水侧温度测量数据(实验值)与模拟结果(模拟值)进行对比,入口温度随该日逐时冷负荷的变化而变化. 夏季制冷工况下,供、回水侧温度模拟值与实验值的对比,如表3所示.表3中:θexp为供、回水侧温度的实验值;θc为供、回水侧温度的模拟值;η为供、回水侧温度的实验值和模拟值的相对误差. 由表3可知:模拟值与实验值吻合较好,两者之间的相对误差不超过3%,误差产生的原因可能是实验中的埋管以管群形式存在,各埋管相互之间有一定的干扰;模拟值与实验值的误差相对较小,且在允许范围内,故该模型具有准确性. 表3 供、回水侧温度模拟值与实验值的对比Tab.3 Comparison between simulation values and experimental values of water supply and return side temperatures 无量纲贝克莱数是渗流产生的对流和热传导的影响程度比值,可用于判断地埋管换热器换热受地下水影响的大小,其表达式为 Pe=ρucuvlm/λtot. (14) 式(14)中:Pe为贝克莱数;ρu为地下水的密度,kg·m-3;cu为地下水的比热容,J·(kg·K)-1;v为地下水的流速,m·s-1;lm为特征长度,文中为含水层厚度,m. 由贝克莱数的表达式可知,其大小受lm,v,λtot的影响,而λtot与λs,φ有关.为了研究地下水对地埋 图3 Δqi随Pe的变化情况(lm=20 m)Fig.3 Variation of Pe with Δqi (lm=20 m) 管换热器的换热作用,分别模拟不同的含水层厚度、地下水流速和岩土体孔隙率对Δqi的影响. 假设含水层的顶部位于深度27.6 m处,当含水层厚度为20 m时,模拟地下水流速分别为3.0×10-5,2.5×10-5,1.5×10-5,1.0×10-5,7.0×10-6,5.0×10-6,3.0×10-6,1.0×10-6m·s-1的情况,可得到该层单位井深换热量增加率.同时,在上述地下水的流速下,模拟岩土体孔隙率分别为20%,30%,40%,50%,60%,70%,80%的情况,可得到该层单位井深换热量增加率.Pe的范围为46.842~2 810.520,Δqi随Pe的变化情况,如图3所示. 由图3可知:地下水对地埋管换热器换热具有促进作用,但当地下水流速较低或岩土体孔隙率较大时,地下水反而会对换热产生抑制作用,即Pe为46.842~93.684时,单位井深换热量增加率Δqi小于0;在含水层厚度为20 m的情况下,当Pe大于140.52时,地下水对地埋管换热器换热产生显著影响,当Pe小于140.52时,单位井深换热量增加率Δqi小于0.001,地下水对换热的影响远小于导热,地下水的作用可以忽略. 将Pe与Δqi进行拟合,得到当含水层厚度为20 m时,Δqi随Pe的变化方程为 (15) 式(15)中:R2为拟合度. 不同含水层厚度的情况下,Δqi随Pe的变化情况,如图4所示.图4中:含水层厚度为5,10,15,25,30 m时,对应的Pe取值范围为[11.71~702.63], [23.42~1 405.26], [35.13~2 107.89],[58.55~3 513.15],[70.26~4 215.78]. 不同含水层厚度对应的Pe临界值,如表4所示.表4中:Pecr为Pe的临界值. 图4 Δqi随Pe的变化情况 Fig.4 Variation of Pe with Δqi 由图4和表4可得以下3个结论. 1)Pe的临界值随着含水层厚度的增加而增大;当Pe大于临界值时,地下水对地埋管换热器换热的影响比较显著;当Pe小于临界值时,地下水对地埋管换热器换热的影响可以忽略. 2) 随着含水层厚度的增加,含水层单位井深换热量增加率逐渐减小;当含水层厚度小于15 m时,单位井深换热量增加率最大时接近0.5;当含水层厚度大于15 m时,单位井深换热量增加率最大值逐渐减小;当含水层厚度为30 m时,单位井深换热量增加率仅为0.32;当含水层厚度一定时,单位井深换热量增加率的曲线斜率随着Pe的增大而减小. 3) 并不是含水层厚度越大,其换热效率就越高,地下水的作用具有一定限度.在Pe较小的情况下,地下水作用增大,导致换热量变化的幅度更加明显. 当含水层厚度分别为5,10,15,25,30 m时,单位井深换热量增加率Δqi和Pe成对数关系.Δqi和Pe之间变化关系的拟合曲线方程分别为 表4 不同含水层厚度对应的Pe临界值Tab.4 Critical values of Pe with different aquifer thicknesses Δqi=0.222 5ln(Pe)-0.966 7,R2=0.996 5, (16) Δqi=0.194 0ln(Pe)-0.859 5,R2=0.997 3, (17) Δqi=0.162 2ln(Pe)-0.754 1,R2=0.995 2, (18) Δqi=0.132 6ln(Pe)-0.704 0,R2=0.993 8, (19) Δqi=0.110 9ln(Pe)-0.587 2,R2=0.997 7. (20) 在含水层厚度不同的情况下,地埋管换热器在地下水作用下的单位井深换热量增加率随Pe变化的曲线方程为Δqi=aln(Pe)+b.其中,系数a,b随lm的变化而变化. 通过拟合,可以得到a,b关于含水层厚度lm的曲线方程,分别为 (21) (22) 由于每层岩土体的单位井深换热量不同,可以通过各层岩土体的厚度和导热系数的比值,得到各层岩土体的分层单位井深换热量[2],即 (23) 式(23)中:λi为第i层岩土体的导热系数,W·(m·K)-1. 式(23)将地埋管换热器换热的热流密度分为平均部分和加权部分,平均部分反映钻井内部均匀的换热量,加权部分则反映不同外部岩土体产生的差异.该公式在不考虑地下水作用时比较准确,但当地下水的作用较为明显时,加权部分会产生较大的误差.如果将渗流作用考虑在内,则需对含水层处的导热系数进行修正.假设计算区域内的岩土体轴向分为n层,其中,第m层为含水层,通过Δqi和式(23),可得修正导热系数公式为 . (24) 通过COMSOL仿真软件,建立地埋管换热器的轴向-周向二维模型,并将钻井等效为长度为70 m的线热源,其顶部距离地表5 m.根据文献[11]的方法,对计算区域进行竖向分层.其中,含水层深度为27.6~37.6 m,地下水流速为1×10-5m·s-1,流动仅存在于水平方向.通过式(14)进行计算,可得Pe为409.3.通过式(12),(13),(24)进行计算,可得修正后的各层导热系数及岩土体的分层单位井深换热比率,结果如表5所示. 将各层岩土体的单位井深换热量代入对应的线热源模型,可建立新模型. 表5 各层岩土体的相关参数Tab.5 Related parameters of rock-soil in each layer 对新模型分别进行短期模拟和长期模拟,通过地埋管换热器周围岩土体的温度分布对模型进行验证.短期模拟是将新模型与Fluent模型分别模拟4 d,对比模拟结束后距钻井壁0.5 m处岩土体温度的轴向变化,以及地下水下游的钻井壁温度在埋深35 m处随时间的变化,以此验证新模型的准确性. 新模型与Fluent模型的模拟对比,如图5所示.图5中:θb为钻井壁温度. (a) 岩土体温度 (b) 钻井壁温度 图5 新模型与Fluent模型的模拟对比Fig.5 Simulation comparison between new model and Fluent model 由图5可得以下4个结论. 1) 两个模型的误差在5%以内,变化趋势几乎完全相同,新模型的温度略高于Fluent模型,这可能是因为新模型忽略了回填材料对换热的影响. 2) 在含水层区域,由于受到地下水的影响,岩土体的热扩散能力有较大的提升,地埋管换热器供水侧岩土体温度几乎与初始温度相同,温差不超过0.5 ℃. 3) 在地下水流动的下游,在4 d的运行后,两个模型在埋深35 m处钻井壁温度随时间变化的曲线趋势基本相同,误差很小,最大误差仅为4.2%. 4) 新模型对短时间内岩土体温度场分布的模拟较为准确,而且新模型的计算时间远小于Fluent模型,对于整个供冷期的模拟时间仅为286 s左右.在研究地埋管换热对岩土体温度分布的影响时,新模型具有较大优势. 图6 岩土体温度的轴向变化Fig.6 Axial variation of rock-soil temperature 长期模拟是对整个供冷期进行模拟,可得地下水下游距钻井壁2.5 m处岩土体温度的轴向变化,如图6所示. 由图6可得以下2个结论. 1) 新模型与实验数据的误差在10%以内,误差在工程允许范围内,故新模型对长期温度场分布的模拟具有较高的准确性. 2) 相较于实验数据,新模型产生的误差主要集中于地埋管换热器的后半段,这是因为新模型中分层换热量的大小与各层岩土体的厚度具有相关性,在导热系数和各岩土层厚度确定时,各层单位井深换热比率不变,故分层单位井深换热量仅随输入负荷的变化而变化. 实验数据取自黄土高原地区某处土壤源热泵系统,在此系统中,虽然50~70 m处岩土体的导热系数较高,但由于热回流的存在,导致地埋管换热器在57~70 m处的换热效率很低,因此,新模型在后半段产生较大的误差,新模型对埋深合理的地埋管换热器的准确性更高. 基于黄土高原地区某土壤源热泵的实验数据,通过Fluent流体仿真软件建立地埋管换热器三维非稳态分层换热模型,并借助实验数据对模型的准确性进行验证. 在不同的含水层厚度、地下水流速和岩土体孔隙率的条件下,利用该模型分析贝克莱数与地埋管换热器换热之间的关系.通过含水层处换热量增加率,对导热系数进行修正,进而可得到计算速度更快的换热模型.由此得到以下3个结论. 1) 当含水层厚度为20 m时,对不同地下水流速、岩土体孔隙率的情况下,地下水对地埋管换热器的单位井深换热量增加率进行模拟.由模拟结果可知,在以含水层厚度为特征长度的情况下,贝克莱数存在临界值,当贝克莱数大于临界值时,地下水对地埋管换热器换热具有促进作用.在流速较小或岩土体孔隙率较大的情况下,地下水反而对地埋管换热器换热起到抑制的作用. 2) 对含水层厚度分别为5,10,15,25,30 m的情况进行模拟,得到不同含水层厚度下贝克莱数的临界值.同时,通过模拟数据可知,单位井深换热量增加率与贝克莱数成对数关系.建立不同含水层厚度的贝克莱数与单位井深换热量增加率Δqi之间的方程,方程的形式为Δqi=aln(Pe)+b,并通过数据拟合得到a,b关于含水层厚度的方程. 3) 通过单位井深换热量增加率对含水层处的导热系数进行修正,利用修正后的导热系数,可得到分层单位井深换热量,进而建立新的地埋管换热器分层渗流传热模型.将新模型与Fluent模型、实验数据进行对比,可证明无论是短期模拟,还是长期模拟,新模型用于地埋管换热器周围岩土体的温度场分布研究时具有较高的准确性,且计算耗时较短.1.5 网格独立性检验
2 模拟与结果分析
2.1 评价指标

2.2 模型的验证
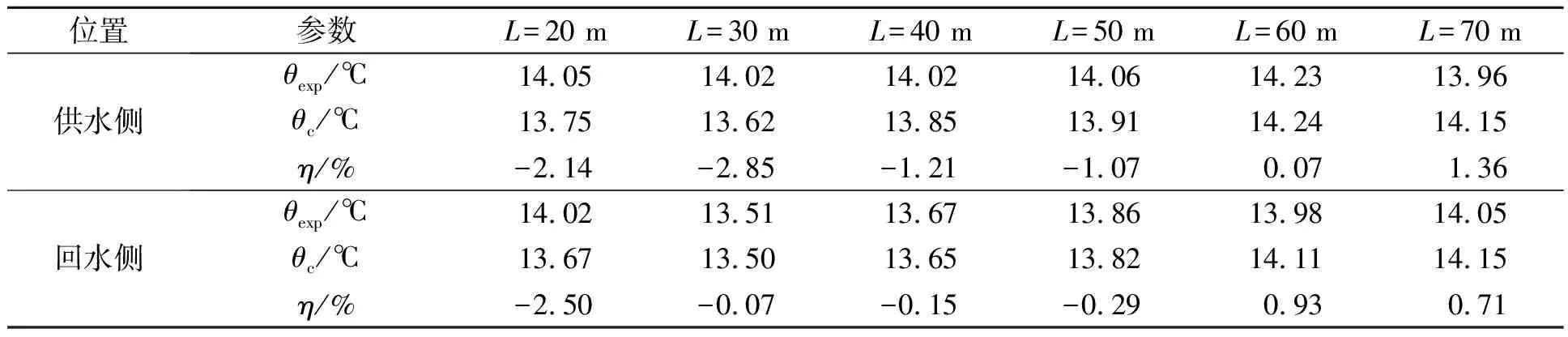
2.3 地下水对地埋管换热器换热的影响
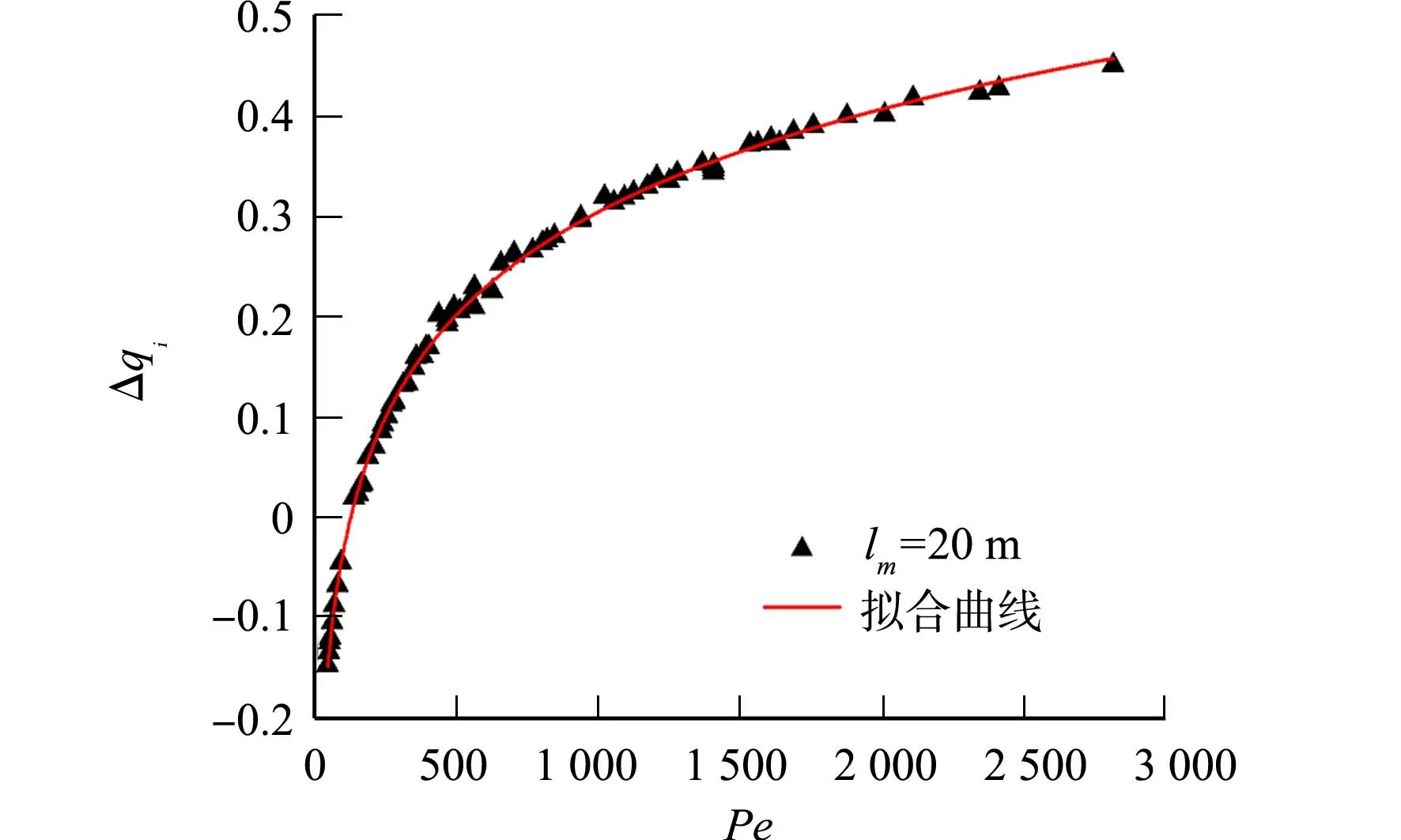
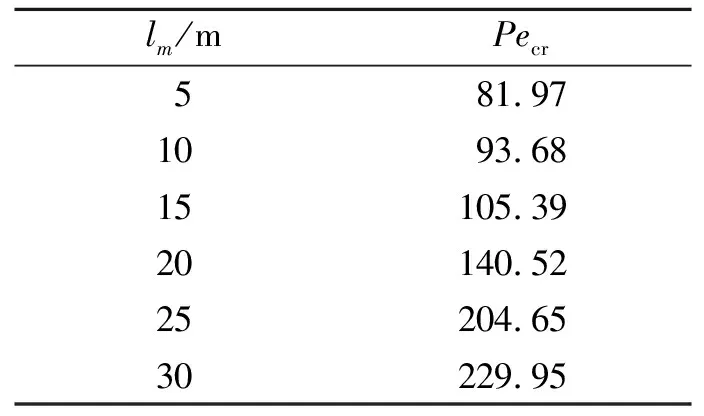
3 新模型的建立与验证
3.1 修正导热系数

3.2 新模型的验证



4 结论
