三维力传感器的设计和静态解耦算法研究*
2022-01-17彭小武马国鹭涌宋子军王清清
彭小武马国鹭*赵 涌宋子军王清清
(1.西南科技大学制造过程测试技术教育部重点实验室,四川 绵阳 621010;2.中国航发四川燃气涡轮研究院,四川 绵阳 621010;3.航空发动机高空模拟技术重点实验室,四川 绵阳 621010)
近年来,随着科技革命的不断深入,传感器的应用领域逐渐宽泛。如在风洞测力试验、飞机称重、智能机器人、军事国防等领域,三维力传感器都是获取感知信息必不可少的器件。通过三维力传感器获取空间各分量力的大小,但由于传感器在设计结构、制造工艺上仍需极大改进,这也导致传感器在测量空间各分量力时会出现不同程度上的维间耦合,在大量程,高精度的测量领域更是如此。而在实际应用中,要使传感器各维间的干扰尽可能的降低,机械结构简单,以满足测量的精度要求[1]。
突破多维力传感器维间耦合的难题一度成为国内外学者们的研究热点[2]。
一是通过机械解耦途径解决。张海霞、崔建伟等[3]设计的一种基于结构解耦的新型应变式三维力传感器。它的弹性体是由两组二维通槽通孔结构的力传感器和横梁组成,测力点位于横梁中心,使得传感器自身结构存在很好地解耦性能[4-5]。吴强、俞志伟等[1]设计的一种小型电阻应变式三维力传感器,其新颖之处在于使弹性体尺寸减小到与应变片尺寸为同一个数量级,既省去加工(形成应力集中位置),又减小传感器的体积。二是通过优化解耦算法。张景柱等[6]开发了一种基于最小二乘法[7-10]线性解耦算法的集成解耦模块。茅晨等[11]提出了基于耦合误差建模的静态解耦算法并结合实验验证,得到了很好的效果。崔劲等[12]采用基于全回归线性解耦算法,对比传统的基于求广义逆矩阵线性静态解耦得到更高的解耦精度。
目前,传统静态解耦算法大多针对小量程的多维力传感器,对于量程大的传感器的计算精度有待提高。本文结合机械解耦方式和解耦算法研制出一种大量程,高精度的三维力传感器。该传感器采用如图1所示的弹性体结构设计,基于最小二乘法线性解耦,为防止解耦过程中出现病态矩阵,取多次试验数据中最为精确的值,将其进行拟合,得到静态线性解耦矩阵[13]。该传感器建立起负载与输出电压之间的数学关系,从而获得空间三维力的大小。

图1 主弹性体结构示意图
1 传感器三维力学分解设计
三维力传感器主要由弹性体、电阻应变片与测量电路三部分构成。对弹性体施加单向载荷,粘贴在应变梁上的电阻应变片产生微变形,根据电阻应变计测量应变的理论可知,弹性体在载荷的作用下,电阻丝的电阻变化率与应变是成一种线性的关系,其数学关系式即:

式中:dR/R为电阻变化率;K为单根金属丝的灵敏系数,ε为金属丝材料的应变值;dL为金属丝长度伸长量(m);L为金属丝的长度(m)。通过式(1)可知,应变值ε随电阻丝的变形发生相应地变化,而电阻值的变化又由电阻应变片组成的电桥测量电路将机械量转变成电信号,再通过惠斯通电桥组桥的方式,建立起载荷与输出电压间的数学关系。
从传感器结构设计上进行优化改进,弹性体采用十字梁型结构,竖梁两侧开设通槽,并将电阻应变片合理粘贴于竖梁和横梁两侧。通过搭建惠斯通全桥测量电路,使其他分量的载荷所产生的电阻增量尽可能不改变电桥的平衡状态,实现传感器在结构上对力和力矩的机械分解或部分机械分解。
在三维力传感器中,弹性体一端与被测物体相接触,一端连接着三维力传感器外壳,是主要的承力结构部件。此传感器采用等截面梁式弹性元件设计,对传感器主体中心(加载帽)施加集中载荷,贴在横梁和竖梁上的应变片发生形变,再通过测量电桥输出为电压[14]。弹性体三维结构模型如图2中(a)图所示。

图2 三维模型及应变片贴片位置示意图
因弹性主体结构不同,则在受力后会,不同部位所产生的应变量也不同,并且各应变量之间存在着巨大的差异。为保证设计的三维力学传感器有足够好的应变灵敏度,电阻应变片的粘贴位置,如图2中(b)图所示。
三维力学传感器的X、Y方向应变域均贴有4片电阻应变片,Z轴方向应变域共有4×4=16片(正反面各贴有8片)电阻应变片,整个三维力学传感器共24片电阻应变片。组成6个惠斯通全桥电路,X、Y、Z三组测量电压的输出信号。
图3为简化桥路用于测量X/Y/Z方向的力,当在力F Z的作用下,桥路1中有8个应变片位于压应力区,另外8个应变片位于拉应力区,使电桥获得最大输出。R a(a=1~4)表示为四个应变片组成的一个全桥。同理,R b/R c/R d依次类推。由于电阻应变片的压变效应,电阻值的变化量经惠斯通电桥转变为电压输出信号,就可得到作用在Z方向的力F Z的大小,实现负载与电压之间的转化。

图3 电压输出电路
当测量X方向的力F X、Y方向的力F Y时,R a/R b/R c/R d表示为四个电阻应变片。在F X或F Y作用时,利用惠斯通电桥的和差特性可知,相邻桥臂电阻反向变化,这时产生的电压输出相互叠加,电桥获得最大输出。反之,输出电压相互抵消。三维力学传感器的电阻应变片均采用等臂全桥接法,即所有电阻应变片的阻值均为R。在连接桥路时,为保证惠斯通电桥拥有较高的灵敏度,同时也能降低因灵敏度过高所产生自我响应对实验数据造成的影响。故采用相互对称的连接方式,即相邻桥臂上的电阻应变片产生应变的方向相反,而相对桥臂上的电阻应变片产生应变的方向相同。
2 传感器的标定
整个标定实验平台由电子万能试验机、标定加载台、数据采集装置等搭建组成。而对传感器数据的采集以及分析处理采用的是德国福公司研发的TwinCAT PLC Control系统,最终完成了三维力传感器的静态标定。通过电子万能试验机对三维力传感器进行标定加载试验,如图4所示。

图4 传感器标定装置实物图
在计算三维力学传感器标定时,理想情况下,只需考虑单方向产生的应变,通过应变片桥路的转化后所得到的电压信号只对被测力的某一个分量敏感,不必考虑受其余分量的影响。由于三维力传感器的结构和制造工艺等原因,单向力作用在3个应变梁上均会产生应变并输出数据。因此,维间耦合使三维力传感器的测量精度受到明显影响。为实现三维力学传感器的准确标定,从建立数学模型着手,采用最小二乘法对实验数据进行拟合,得出三维力学传感器标定的算法。
对三维力学传感器施加单向集中载荷力F,则三坐标轴的3个分力分别为F X、F Y、F Z,传感器在三坐标轴上相应的应变εX、εY、εZ经惠斯通电桥组桥电路处理后的输出信号分别为U X、U Y、U Z。显然,此3个输出信号是输入量F={X,Y,Z}T的函数,即:
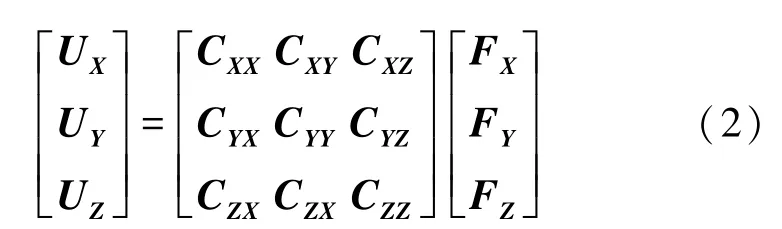
用矩阵形式可表示为U=C×F,式中U为各分量输出的电压值,C为解耦矩阵,F为外加载荷。解耦矩阵可以通过静态标定得到,其反应了各维输入载荷与输出电压之间的耦合关系。解耦矩阵中C XY表示的含义为:在Y方向施加载荷时,X方向上的电压输出值,其余元素含义同理。
为防止出现病态解耦矩阵对实验结果产生干扰,对传感器进行重复性加载试验,将较为精确的几组数据进行拟合。实验基于微型电子万能试验机,按照国家标准对传感器进行施加载荷,设置加载速度为0.1 mm/min,每个负荷按照一定梯度加载并保持时间暂定2 min使其达到稳定。通过万能试验机分别对X、Y、Z方向按照4 kN的级差作为一个测量点进行单向加载试验,将得到的部分标定数据如表1所示。

表1 力传感器标定数据表
3 解耦测试分析
通过最小二乘法将表1中的数据进行拟合成线性曲线,如图5所示。将该直线转化成y=kx+b的形式,故该直线的斜率k对应于解耦矩阵C中的一个元素。

图5 Fx、F y、Fz方向标定结果曲线

根据图5的Fx、Fy、Fz方向标定结果曲线可获得解耦矩阵C:联立式(1)~式(3)可知,对弹性体三个分量分别进行加载试验,可以计算出各桥路输出的电压值。反之,已知X、Y、Z桥路输出的电压值通过矩阵求逆便可得到施加在弹性体上的力,即

将解耦算法写入数据采集系统程序中,进行解耦验证。通过万能试验机分别对X、Y、Z方向进行单向加载试验,再对比分析解耦矩阵计算得到的实际三维力,其误差值如表2所示,可以得出X、Y、Z方向加载力的Ⅰ类误差(静态非线性率)最大值为2.36%。

表2 力传感器解耦测试结果对比表
通过Ⅱ类误差(静态耦合率)表征传感器各方向间的耦合程度[15],经实验数据计算可知:Z方向与X、Y方向的耦合率分别为0.62%、2.1%,X方向与Y方向的耦合率为0.064%,即Z方向加载时,Z方向与Y方向最大维间耦合误差为2.1%F.S。
利用以上方法对该传感器各维间进行多次重复性验证试验,整理出部分相关数据,如表3所示。

表3 传感器部分参数表
4 结论
①设计了一种新型的电阻应变式3维力传感器,通过改进弹性体的结构以及应变片排布方式,有效减小了传感器的体积,从机械结构解耦的途径进一步提高了弹性体本身的解耦性能。
②试验结果表明,该传感器主分量(Z向分量)保证Ⅰ类误差控制在2.36%范围内,Ⅱ类误差最大值仅达到2.1%,传感器的测量精度显著提高,验证了传感器有较好地解耦性能,攻克了各分量量程大且极度不匹配的难点,能够满足实际应用的需求。
