基于改进随机森林模型的水质BOD快速预测研究*
2022-01-17涌陆卫左楚涵鲍明月
王 涌陆 卫左楚涵鲍明月
(1.浙江工业大学计算机学院,浙江 杭州 310014;2.浙江工业大学奉化智慧经济研究院,浙江 宁波 315500)
BOD(Biochemical oxygen demand,生化需氧量)是水体中微生物分解所需消耗溶解氧的含量,它能够直接体现水质的污染程度[1],是水质监测等行业关注的重要污染指标。对于传统BOD测量方法,主要存在设备昂贵易损坏难维修、需要离线采样分析测量、测量耗时五天、需要专业人员操作等问题,这给污水监测行业带来困扰。为了解决以上问题,现今已有一种软测量方法能够测量BOD。软测量方法[2-4]指通过数学理论分析处理数据,建立数据集中简单易测的辅助变量与复杂难测的目标BOD之间的机器学习模型,将包含辅助变量与BOD的数据集用来校正模型,最后可以通过将辅助变量数据输入模型来预测BOD值[5]。
近年来,由于机器学习的迅猛发展,BOD软测量模型的精度已经能够媲美BOD传统测量法的精度,同时相比传统BOD测量方法有效减少耗时,为监测行业提供了更优秀的选择。Zhang[6]等人通过SOM网络来预测BOD的浓度,通过分析选择了氨氮、SRP、SS、COD作为模型的辅助变量,最终模型在样本有大量缺失值仍有不错的精度,且测量时间可以缩短到几小时,但是仍不适合实时BOD的预测。Raheli[7]等人通过萤火虫FFA算法来优化多层感知机MLP,通过实验有效表明了MLP-FFA能够预测BOD值,但是由于模型的d因子导致模型不稳定,从而造成模型精度不佳。许玉格[8]等人提出了一种Fast-SVM模型,有效提高了BOD模型的预测速度,但相较于基础SVM模型,精度有所下降,同时文中将所有的辅助变量作为模型输入,导致模型计算量过大。乔俊飞[9]等人通过PSO算法改进ESN神经网络,且通过对水质BOD机理分析,选择了pH、SS、DO、COD作为ESN的辅助变量,实验证明了PSO算法能够更有效找到ESN网络的权重,使得ESN网络的预测精度提高,但由于网络的复杂性,仍不能满足本文的实时BOD预测场景。以上对于BOD软测量模型的研究,仍存在两个问题:①对于大数据时代的今天,数据应保证精度同时也应保证时效性。因此模型预测速度也是重要的性能评判指标。上述研究中通过研究不断加大模型复杂度来提高精度,而导致模型预测速度大幅下降,这显然是不合理的。②辅助变量的选择都是根据经验选择,没有确切的选择依据。
根据这两个问题,本文通过对随机森林(Random Forest)模型的研究[10-11],提出了一种快速且精度高的改进随机森林模型来预测BOD值,本文的主要研究如下:
①提出了一种基于特征重要性排序算法和LDA(Linear Discriminant Analysis,线性判别分析)的随机森林模型来快速预测BOD值。随机森林模型由于其随机性是一种强大的回归模型,非常适合BOD预测。特征排序能够筛去对模型影响较小的辅助变量,LDA能够对辅助变量降维,减少噪声和冗余数据对模型精度的影响。改进后的模型在精度和预测速度上有明显提升。
②将改进随机森林模型与当前主流的BOD预测模型,支持向量机模型和全连接神经网络模型进行横、纵向对比实验。通过纵向实验,找到每个模型的最佳参数。通过横向实验对比三个模型性能,实验结果有效表明了本文提出的改进模型在快速BOD预测场景下的优势。
1 特征重要性排序算法
1.1 决策树
决策树主要用于表达选择。决策树分为三个部分,分别是根、内部、叶子节点[12]。根和内部结点都表示一种特征,叶子节点表示结果。决策树从根结点开始,通过内部结点到叶子结束。因此根结点是较好的特征,需要有较好的分类能力。因此决策树模型首先要选择一个最好的特征作为根结点。选择最好的特征时要以不同特征的信息增益作为准则,信息增益大的特征有更好的分类能力。
1.2 信息增益
熵用来表达随机变量的不稳定性,表示数据内部的混乱程度。在一组数据中随机变量X为离散值时,即X的取值为x i,此时随机变量X的概率分布为:

式中:n为样本量,则随机变量X的熵为:

熵值越大,系统越混乱,不确定性也就越大。当概率为0或1时都是确定的量,不会有不确定性,因此概率为0或1时不会影响熵值。
条件熵表示为H(Y|X)为在随机变量X条件下随机变量Y的不确定性。

信息增益能够确定决策树中的各个特征,哪一个特征对于模型学习最有用,即信息增益可以描述特征对各个子集分类效果的好坏。

式中:g(D,A)表示特征A对数据集D的信息增益,用经验熵H(D)与给定特征A条件下的数据集D的条件熵做差得到。信息增益不适用于特征类别较多的情况,因为此时会发生过拟合问题[13]。
若根据特征A的取值可以将数据集D划分为n个子集D1,D2,…,D n,其中n是特征A可能取值的种数,则数据集D关于特征A的值的熵H A(D)为:

此时信息增益比g R(D,A)为:

1.3 特征重要性排序算法
在决策树生成时有两种算法,ID3与C4.5,分别对应以上介绍的信息增益和信息增益比为基础的两种算法[14]。表1将ID3和C4.5算法生成的预剪枝决策树过程表示出来。

表1 预剪枝决策树生成算法
生成预剪枝决策树后,这样特征重要性就可以通过随机森林中每一个决策树的基尼指数得到。将基尼指数记为G,如果数据集D分类问题中有K个类,某个子集属于第k类的概率为p k,则基尼指数为:

在决策树中某个内部结点剪枝前后基尼指数变化量记为V,设剪枝后出现两个新的结点,记两个新的结点的基尼指数为G p,G q,则有下式:

设特征A在决策树T i中出现的结点集合记为M,那么特征A在决策树T i中的重要性记为:

若随机森林中有N棵决策树,那么特征A在随机森林算法中的基尼指数评分为:

最后对不同的特征求得的基尼指数做归一化之后进行排序得到的就是不同特征的重要性排序。在随机森林模型中,通过重要性排序将其中重要性小于0.2的特征筛除。
2 LDA算法
LDA是一种监督学习的降维算法,LDA算法的目的是通过将数据投影到新的坐标系中,令新的数据满足同一类别的数据中方差最小,不同类别的数据方差最大。
设数据集为D,数据集总共分为k类,则将数据集D分为D1,D2,…,D k,其中每一类数据集中数据的个数为N1,N2,…,N k,即:


若假设uTu=a,则在D k中样本方差为:

将D1,D2,…,D k不同数据集之间的样本方差求和得到:

不同类别D i与D j之间的方差为:

不同类别D之间的方差和为:

因此最后要求解的问题为:

LDA的目的是令uTS b u最大,同时令分子uTS w u最小,即求解优化问题maxJ(u)。为了令问题简化,由于uTu=a,因此可以通过改变a的值令uTS w u=1,那么优化问题就变成了maxuTS b u。通过拉格朗日乘数法,将优化问题转化为拉格朗日函数:

通过求解偏导得到:

通过S b u=λS w u得到S-1w S b u=λu,即求解特征向量。因此对S-1w S b进行奇异值分解,得到特征值λi对应的特征向量为u i,取前三个最大的特征值对应的特征向量组成投影矩阵W。通过求出数据在这三个特征向量上的投影,将输入辅助变量数据降到3维。
3 基于特征重要性排序和LDA降维改进的随机森林模型
3.1 随机森林算法
随机森林算法采用CART决策树[15-16]进行回归,以最小二乘法作为CART决策树的基准。随机森林算法首先从原始数据集中有放回的选取m个数据,重复n次,这样就得到了n个新的数据集,这些数据集作为基学习器的训练集得到了n个决策树。
每个数据集总特征中随机选择k个特征,并用这k个特征作为CART决策树生成中所用的特征。在回归问题中随机森林通过对全部基学习器得到的预测值采用简单平均法得到最终的预测值:

3.2 基学习器的个数
随机森林的基学习器个数对模型有显著的影响,因此确定基学习器的个数至关重要,当个数过少时会导致模型精度不够,当个数过多时会造成过拟合。
为了解决个数确定问题,本文采用了一种十折交叉验证法来确定最优子树(基学习器)数目,以保证随机森林算法模型在水质BOD预测时效果最好。
首先设置基学习器个数为10,对于固定的基学习器个数,对训练数据随机划分为10份,记为K1,K2,…,K10,选择其中9份数据作为训练集,剩下的一份作为测试集,通过训练数据来记录测试集的R2_score(决定系数)。遍历每一份数据,并记录每一次得到的R2_score值,最后通过对得到的10个R2_score求平均值作为该基学习器数目下的平均R2_score。随后增加基学习器的数目,基学习器数目450作为上限,在这个过程中选择平均R2_score最大时的基学习器个数为最优的基学习器个数。
3.3 随机森林算法模型的改进
本文采用特征重要性排序和LDA算法对随机森林模型的输入模块进行改进,其中特征重要性排序是由随机森林算法得到的,因此基于特征筛选和PCA降维的随机森林模型的效果将会明显优于其他传统的机器学习模型。随机森林能够处理较为复杂的问题,模型的随机性会降低错误数据在整体数据中的比重,而CART决策树的生成方法也会进一步避免一些无效特征对随机划分得到的数据的影响,这样的随机性会让随机森林模型更好的适应本文水质BOD的快速预测问题。基于特征筛选和PCA降维的随机森林模型框架如图1所示。

图1 基于特征筛选和LDA降维改进后的随机森林模型
4 基于改进随机森林的水质BOD快速预测模型的应用
4.1 数据分析处理与实验方案
本文数据来源于某水质监测厂提供的300组数据,数据包含的变量有:温度Temp、pH、溶解氧DO、大肠杆菌E.coil、悬浮固体SS、浊度Turb、氧化还原电位ORP、电导率EC、硝酸盐、化学需氧量COD、凯式氮、氨氮AN以及本文需要预测的生化需氧量BOD。
由于数据样本中存在较多空缺值,本文采用平均值插补法进行填补。填补之后,通过特征重要性排序算法筛除对模型影响较小的变量,本文以重要性为0.2为基准,其中重要性小于0.2的辅助变量为pH、电导率EC、浊度Turb和大肠杆菌E.coil,这些辅助变量需被筛除,因此通过特征筛选后剩下8维辅助变量。
随后对温度Temp等8维辅助变量数据进行LDA算法降维,LDA根据数据类别降维,最后选择了奇异值分解后模最大的三个特征向量作为向量u1,u2,u3,数据在这三个向量方向上的投影作为降维后的数据。
为了保证实验严谨性,本文对样本数据按8∶2的比例随机划分训练集和测试集,进行5次重复实验得到五组训练集和测试集并分别对未改进的随机森林算法和改进后的随机森林算法分别进行对比实验。其中用于训练的数据数目为240,用来训练随机森林模型以及校正随机森林的参数,验证集的数据数目为60,用来测试评估随机森林模型的性能,最后通过将验证集数据中的辅助变量数据输入随机森林模型,模型输出的预测结果将与验证集中BOD的实际值进行比较,通过误差评价指标和绘图的方式来展示模型的优劣。
4.2 模型性能评估指标
本文使用的模型性能评估指标如下:
①反映模型精度的指标:MSE、MAE。
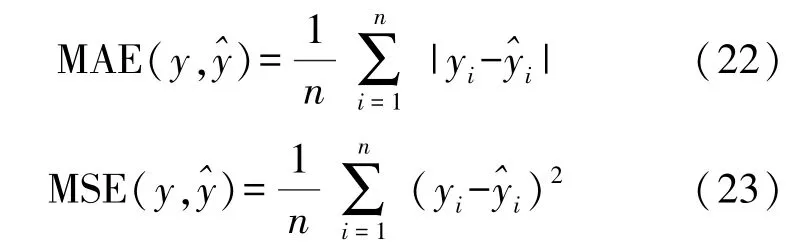
式中:y i为实际值,为预测值,n为测试集样本数。
②反映模型拟合程度的指标:R2_score。

式中:R2(y,)为R2_score,为BOD测试样本数据的平均值。
③反应模型预测速度的指标:预测时间。
4.3 对比实验与分析
对比实验部分首先需要确定改进前后的随机森林模型的最优子树(基学习器)个数。通过对训练数据交叉验证,从最优子树为1至450分别测得模型的R2_score值,其中最大的R2_score值就是最优实验结果。
通过实验得到没有经过改进的随机森林模型在其最优子树为83时R2_score最高,改进后的随机森林模型在其最优子树为161时R2_score最高。
确定两个模型的最佳参数后,分别对其在最佳参数下进行五组随机数据划分实验,随机森林模型的预测如图2,改进后的随机森林模型的预测如图3。

图2 原随机森林模型在其最优子树为83时的五组随机实验预测图

图3 改进后随机森林模型在其最优子树为161时的五组随机实验预测图
通过两图也可发现改进后的随机森林模型能够更精准的预测BOD值,且改进后的五组预测值更为贴近实际值,且五组实验结果重合度较高,表明了改进模型的稳定性较好。
根据两个模型的五组随机实验可以计算得到表2的性能表。
表2中可以得到两种模型的具体性能指标。MSE、MAE反映了模型精度,改进后的随机森林模型在平均MSE上降低了81.15%,在平均MAE上降低了66.86%。R2_score反映了模型拟合程度,改进后的随机森林模型在平均R2_score上提升了18.36%。预测时间反映了模型的速度,改进后的随机森林模型在平均预测时间上缩短了70.85%。

表2 改进前后随机森林模型的五组实验性能指标
对于改进前后的随机森林模型,选取各自最佳的一组实验进行对比,即原随机森林模型的第二组实验与改进后的随机森林模型的第一组实验,两组预测如图4。预测结果也体现了基于特征重要性排序算法和LDA降维算法改进后的随机森林模型能够有效降低噪声以及误差,减少预测时间,更适合快速水质BOD的预测。这是由于未经改进的输入模块包含很多噪声,冗余的特征存在多重共线性,模型会学习到无效的信息,这对模型的精度会有很大影响,采用LDA降维后的数据包含了原数据的主要信息,筛去了不必要的噪声和冗余信息,这使得模型能够学习得更快更准确,因此改进后的随机森林模型对于快速BOD预测能够达到理想的预测结果。

图4 改进前后的随机森林模型最佳实验对比
5 结语
本文针对BOD传统测量存在的问题,提出了一种基于特征重要性排序算法和LDA降维算法改进的随机森林模型用于BOD的快速在线软测量,有效解决了传统测量的离线采样分析耗时长、实验操作复杂问题。对于随机森林模型,经过本文的改进算法后,在MSE上降低了81.15%,在MAE上降低了66.86%,在R2_score上提升了18.36%,在预测时间上缩短了70.85%。改进后的模型不仅提升了预测精度,同时能够在秒级完成预测任务,在BOD的在线快速测量中有着很大的优势。
