GPS重复基线粗差探测方法比较及实例分析

甄 龙，周 楠，王 岚，袁小勇

（1.中国电力工程顾问集团中南电力设计院有限公司，湖北 武汉 430071；2.国网新疆电力有限公司建设分公司，新疆 乌鲁木齐 830063）

1 常用的几种选权迭代法

2）丹麦法

式中，C是根据经验模型而设定调和参数。丹麦法也是以最小二乘平差准则为基准，而后通过对第一次的残差进行逐次迭代，来实现观测数据中粗差的检验。

3）Huber 函数法

2 等价方差-协方差稳健估计方法

2.1 等价方差-协方差稳健估计函数模型

1）模型的建立。对于M估计而言[2]，所构造的ρ函数应满足:

式中，k0的取值一般在1.5～3.0 之间，而

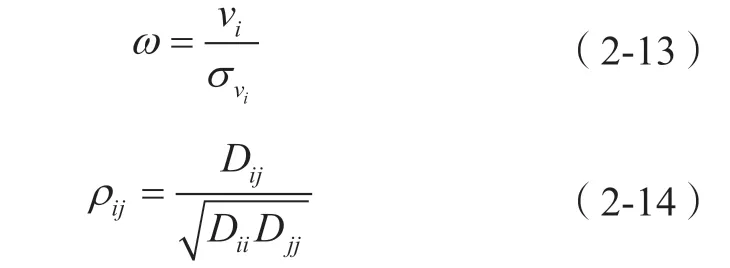
显然，该函数模型具有如下特点:

1）该模型是随机模型的一种体现，它实际上是将方差进行了膨胀处理。

分别于种植体植入后即刻及术后第12周，由同一测量者用OstellTM ISQ种植体稳定性测量仪(BiolinScientifc，瑞典)对种植体的稳定性进行测量，该仪器可将测量结果自动换算为ISQ值(0～100)，分别计为ISQ0(即刻)、ISQ12(12周)；每个种植体各测量两次，取平均值。通过ISQ值比较种植体稳定性变化，分析种植体稳定性与颌骨HU值、性别、种植体型号间的差异。

2）该模型所构造的等价方差-协方差矩阵是具有严格对称性的。

3）在处理独立观测值时，该模型与等价权函数模型计算所得到的结果是相同的；在处理相关观测值时，该模型确保了相关系数大小不变，且所建立的模型与实际情况一致。

2.2 等价方差-协方差调整因子

2.3 相关等价方差-协方差因子

2.4 标称精度改正权相关稳健估计

在保持相关系数ρ不变的条件下

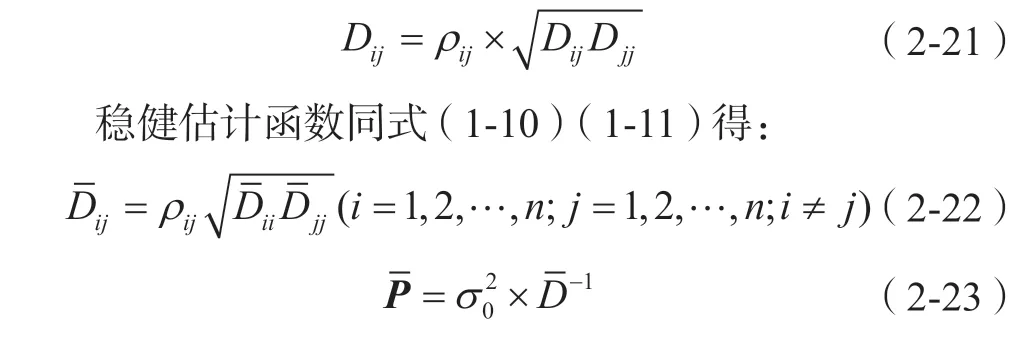
2.5 双因子方差膨胀模型

将粗差归为随机模型时，粗差观测量的先验方差δii2与其实际方差δ^ii2相比较，存在着很大的差异，此时即表现为方差膨胀模型。那么我们可以通过对含粗差观测值的方差进行扩大，从而控制异常观测值的影响[5]。因此提出改进后的稳健最小二乘估计方法，它是在等价方差-协方差阵的基础上建立起来的，可以有效避免等价权稳健最小二乘估计的缺陷。其实质是通过逐次迭代平差计算，并根据所得结果不断将观测值的方差-协方差进行膨胀，直到使异常观测量的先验方差与实际方差相符合，从而达到削弱粗差影响的目的。

观测量的协方差矩阵作为评定观测量精度的指标，能够非常客观地反映出所有观测量的离散程度[6]。若观测值的精度比较高，且可靠性也较好，则其对应的方差也较小，此时赋予该观测量的权重将大，反之则方差大，对应参数估计权重小。

对含粗差观测值的方差进行不断扩大，可以降低其在参数估计中所带来的影响。但由于相关观测量是一个整体，因此仅考虑对方差元素进行膨胀是不够的，还应调整协方差元素。基于各元素之间是相互关联的，应该保证在对方差和协方差进行膨胀之后，其原有的相关系数保持不变。

2.6 异常观测方差膨胀模型

2）方差膨胀模型的相关观测稳健估计算法特点

①上述模型中的方差膨胀因子函数是连续不间断的，它可以很好地控制含粗差观测值所带来的影响。因为方差膨胀函数的取值一般不会为∞，故基于该模型求解时不会删除任何异常观测信息。同时，当方差膨胀系数非常大时，异常观测信息对参数估值将散失作用[7]。

②该模型构造的等价协方差矩阵没有改变观测向量原来就具有的相关性，而且还保证了方差-协方差的对称性。

2.7 方差膨胀因子函数

在构造方差膨胀因子rii时，若观测值误差大于所设定的某种限差，此时相应的方差应该被膨胀。否则令rii取值为1，即是保持原有方差固定不变[8]。所以，rii的构造形式如下:

对于M估计的选权迭代法，当进行k次迭代时，将方差膨胀因子rii取值如下:

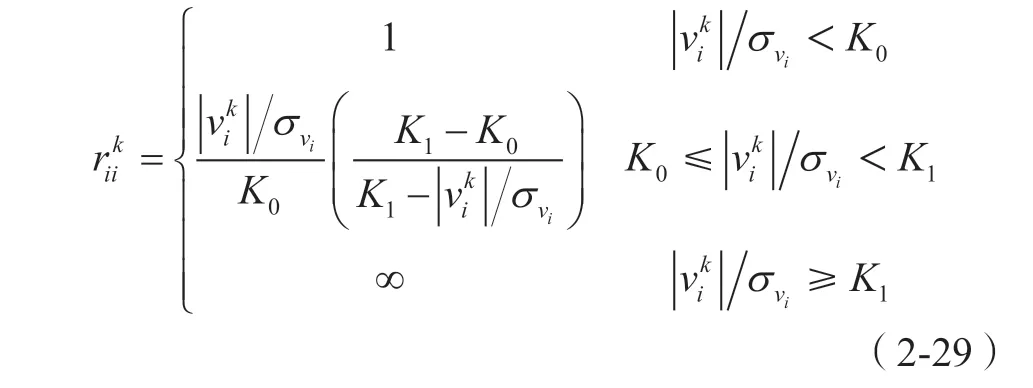
上式类似于IGGIII 权函数的倒数，但为了保证方差膨胀因子更加平稳化，去掉了降权因子上的平方，即有上式中:

3 程序模块算法

基于等价方差-协方差的稳健估计方法与巴尔达数据探测有所不同，其需要再次使用上一次平差的成果，而且对于存在粗差的观测值进行降权而不是删除。首先在处理权阵时，首次平差采用基线文件中提供的方差阵来计算，之后就使用平差所得的方差阵和单位权中误差来计算。

平差过后，需要计算出改正数的方差阵，然后根据公式，计算出新的方差阵，最后再进行迭代。其关键代码如下:

4 基于重复基线时的粗差探测实例分析与比较

结合某高速铁路的GPS 控制网，选取其中一部分，共8 个控制点，20 条基线，其中0360P21 是已知点，原始基线数据如表1 所示。

表1 GPS 向量网各基线向量的观测值

直接对上述不含任何粗差的观测数据进行最小二乘平差计算，各基线向量的改正数结果如表2 所示。

表2 无粗差时各基线向量分量的改正数

现将重复基线CPI1066-0361P21 所在2 个时段观测值的Y方向上均分别加入0.05 m 的粗差，然后分别基于选权迭代法和改进的稳健最小二乘估计法利用已编程序进行计算，其探测的结果如表3～7 所示。

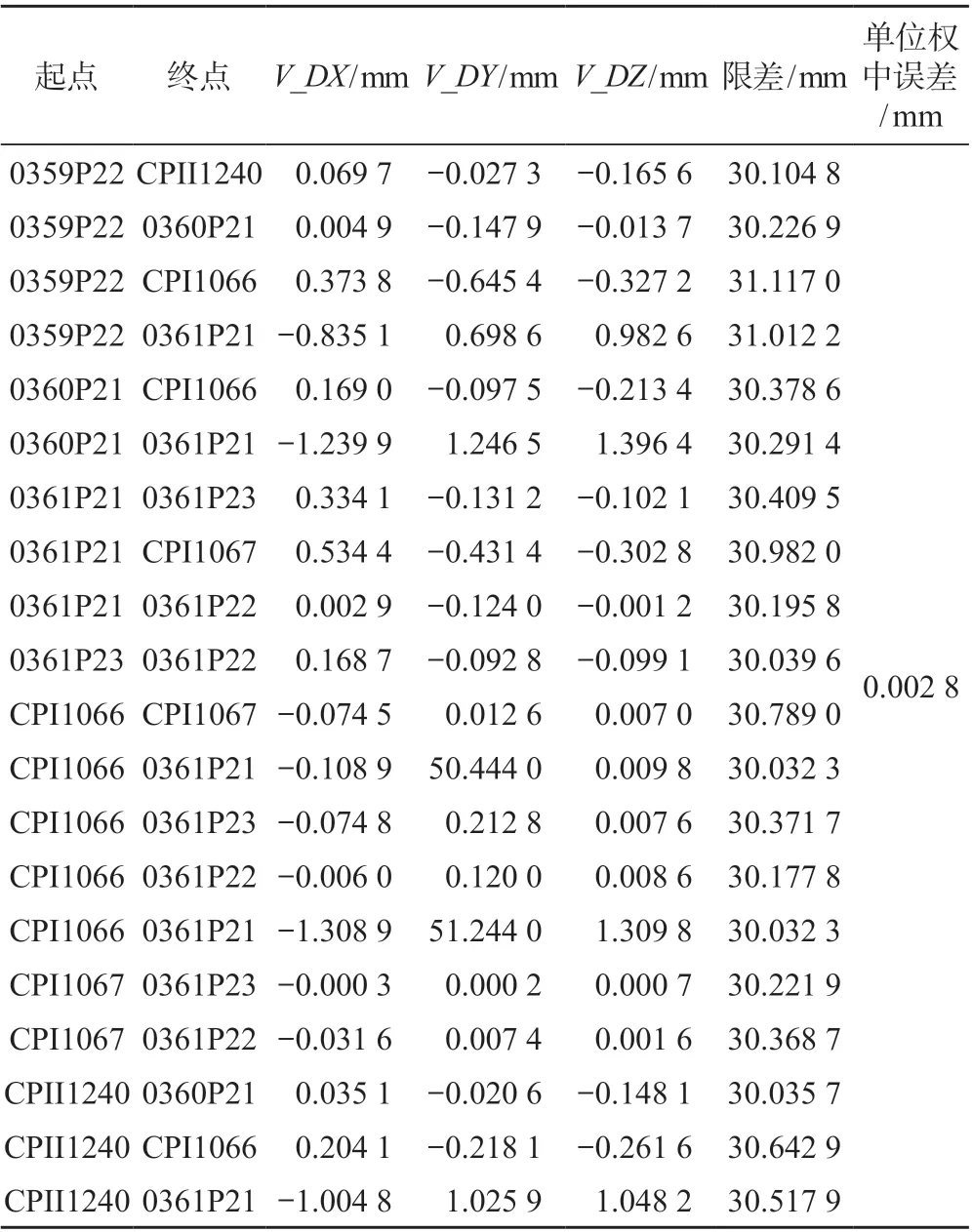
表3 改进的稳健最小二乘估计法粗差探测结果

表4 残差绝对值之和最小法粗差探测结果

表5 丹麦法粗差探测结果

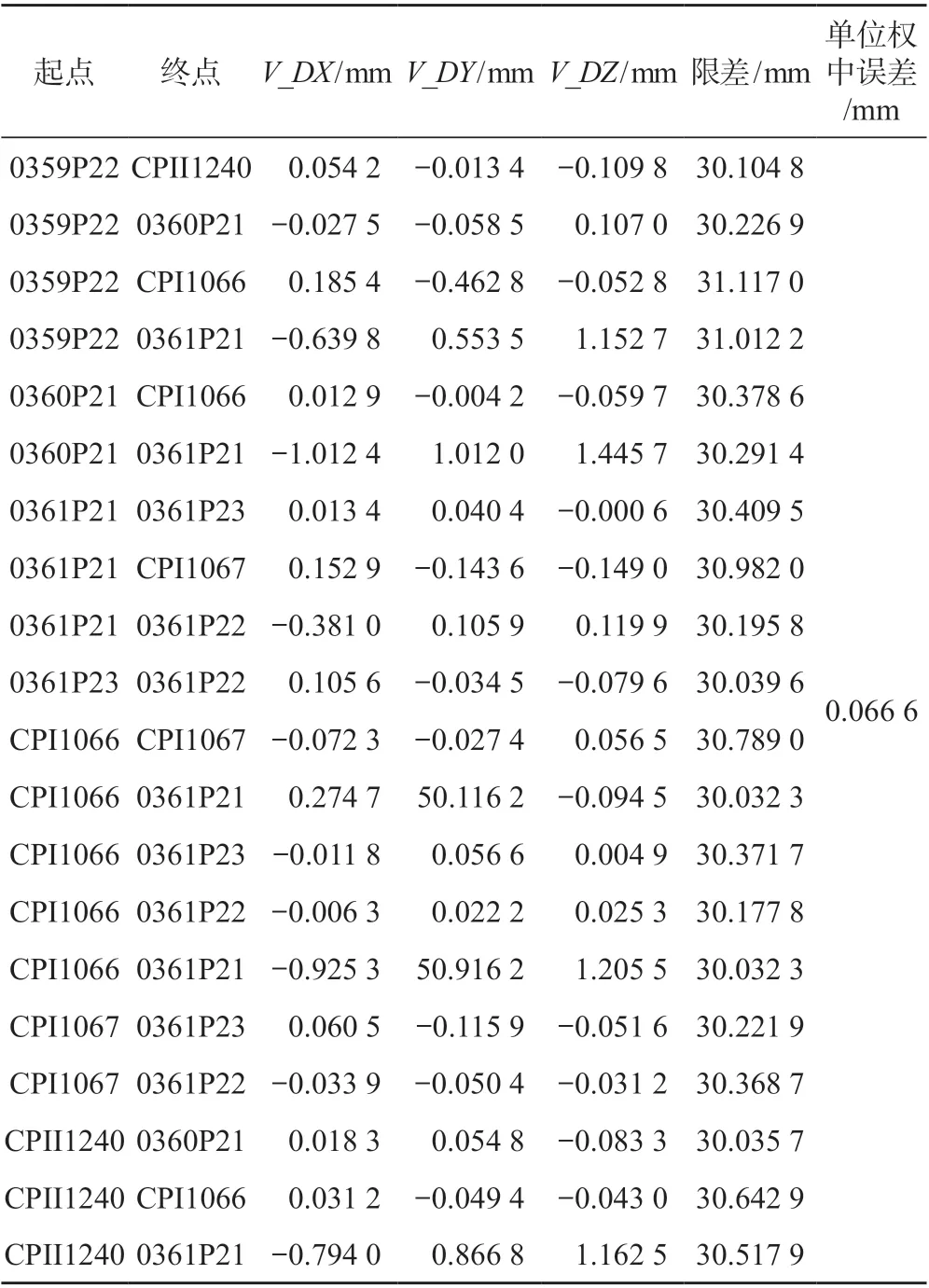
表6 Huber 函数法粗差探测结果

表7 相关性的IGG 法粗差探测结果

根据表3～7 中的粗差探测结果可知:

1）当重复基线上含有粗差时，残差绝对值之和最小法虽然探测到了含粗差的基线向量，但其残差值与实际加入的粗差值相差非常大，均相差近13 cm，同时把原本不含粗差的其余12 条基线向量也认定为含有粗差，没能避免粗差的掩盖和转移现象，探测效果非常差。

2）相关性IGG 法没有探测到超限的基线观测值，且在基线向量的Y方向上，其余原本不含粗差的基线向量改正数均受到不同程度的污染，基本失去抵抗粗差能力。

3）在此次粗差探测中，改进的稳健最小二乘估计法不仅成功定位到了含有粗差基线向量所在的位置，而且对粗差定值也非常准确。然而丹麦法，huber 函数法也均较为准确的探测到了粗差所在位置，但其平差所得单位权中误差均不同程度地大于改进后的单位权中误差，即平差精度不如改进后方法的精度高。

综上，基于重复基线时，改进后的方法无论从定位，定值还是平差精度等方面均优于选权迭代法中的其他几种方法。