变量取值方式对崩塌易发性的影响

赵 玉，陈丽霞*，付 圣

（1.中国地质大学地球物理与空间信息学院，湖北 武汉 430074）

高陡斜坡上的岩土体突然脱离母岩并堆积到坡脚的崩塌现象，极易造成人员伤亡与财产损失，尤其是交通沿线的高陡边坡问题最为突出[1]。在防控崩塌时，对崩塌源区的提前判识是首要任务，其结果的准确性直接影响落石的运动轨迹预测和风险的量化判定[2]。

识别崩塌源区的常用方法有野外地质判断、统计分析或智能模型分析等[3-8]。其中，逻辑回归模型（LRM）是一种广泛用于斜坡地质灾害易发性分析或空间预测的统计分析方法[3-7]。该模型能揭示因变量和多个互不相关的自变量之间的多元回归关系[5]，LRM 的建模过程本身具有挑选变量的优点[6]。随着应用需求的不断提高，目前LRM 已从二元发展到多元，再到与其他模型联合使用的阶段[7]。

在预测模型的使用中，无论何种方式，都面临输入变量取值方式的问题。对于崩塌，其分析因素包括地形地貌、地层岩性、地质构造、人类工程活动等。这些数据以两类方式存在:连续型数据（如坡度值）和分类型数据（如岩性类型）。连续变量的取值方式有变量的原值、变量的归一化值和变量的标准化值。其中，变量的归一化值是连续变量原值与评价单元内的最大和最小值的差值之比获得[8]；变量的标准化值是将变量值标准化到-1 到+1 之间[9]。分类变量的取值类型有属性，分级值、模型处理分级值、数学公式处理分级值和权重分级值，包括根据因子本身属性的分级或者使用某种模型获得的因子对灾害的权重或贡献程度分级。因子属性分级值（如坡度因子），以10°为间隔从小到大分为1 到9 的序号值[10-11]，结合模型处理后的分级值，例如分级后的因子经过信息量模型处理后获得的信息量值[11]；结合数学公式处理后的分级值，例如结合加权频率比模型[12]进行归一化的分级值；权重分级值，如根据专家经验或数学模型对不同因子赋权重，也可以对不同因子的不同级别赋权重，最终获得分级值[13]。可见，变量的取值方式多样，但其对灾害评价结果是否有影响以及影响程度如何，需要进行对比验证。

鉴于此，本文以湖北省利川龙驹坝G318 沿线崩塌为例，使用评价因子的3 种取值方式（原始值、信息量值和信息量排序值），采用LRM 评价崩塌源区识别的差异性，最终选用最优取值方案实现崩塌源的识别。

1 研究方法

在资料收集、遥感解译和野外调查的基础上，利用统计分析方法从地质数据中提取崩塌的主要影响因子，深入研究崩塌的发育规律。因子包括坡度、坡向、曲率、粗糙度、岩性、斜坡结构、节理密度、水系线密度、归一化植被指数（NDVI）、土地利用类型。通过统计崩塌集中分布的坡度，初步筛选出崩塌源范围。之后对崩塌形成内在条件和外在诱因上进行变量提取，采用3 种变量输入方式（原始值、信息量值和信息量排序值），在ArcGIS 内实施崩塌源区易发性评价，用5 类易发性等级（极高、高、中、低和极低）表征崩塌源区发生灾害的可能性大小。最后分别从易发区分布空间特征、极高和高易发区的面积比例和评价精度三方面，判断3 种结果的崩塌源识别能力，技术路线见图1。

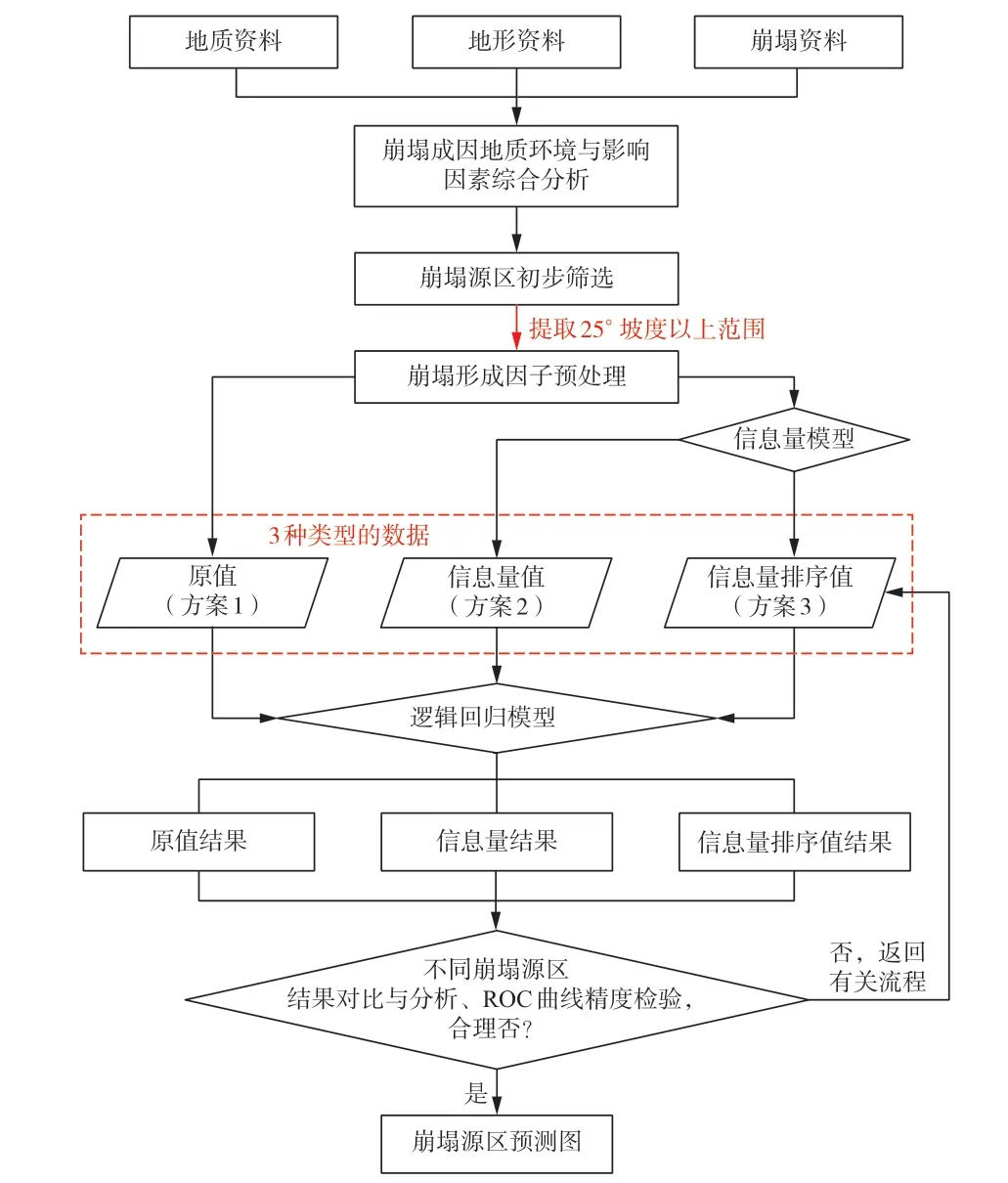
图1 技术路线图

3 种变量取值方案为:

方案（1）通过ArcGIS 提取各个因子的原始值。例如坡度因子以连续型坡度值赋给研究区的栅格单元；斜坡结构因子则以分类型数据进行赋值。连续型数据和分类型数据分别保持原值。

方案（2）通过信息量模型[10]获取各个因子的信息量值。信息量值为分类型，各因子以离散形式输入。

方案（3）是在（2）的基础上，对各因子的各级别的信息量值由大到小进行重要性由高到低的排序后获取其排序值，排序值为分类型，各因子的各级别以离散的编号值输入。

1.1 信息量模型原理

信息量模型最早由殷坤龙[10]提出并用于地质灾害易发性预测，其计算公式为:

式中，I为单元信息量值；Ii为因素xi对地质灾害所提供的信息量；Si为因素xi所占单元总面积；Si0为因素xi单元中发生地质灾害的面积之和；A0为研究区地质灾害的单元面积之和；A为研究区总单元面积之和。

1.2 LRM 原理

LRM 是目前广泛用于地质灾害易发性评价的数学统计模型[3,4,7]，LRM 中表示崩塌的因变量Y是一个二分类变量，其取值Y=1 和Y=0，分别代表发生崩塌和未发生崩塌。影响Y取值的n个自变量因子分别为X1,X2,…,Xn，在n个自变量作用下崩塌发生的条件概率为P=P(Y=1|X1,X2,…,Xn)，则LRM 可表示为:

式中，zi为中间变量参数，无实际意义；a0为回归常数；ai为第i个变量的回归系数(i=1,2,…,n)；Xij为第i号单元中第j个变量的取值，存在崩塌取1，否则取0；Pi为第i号单元内崩塌发生概率回归值(i=1,2,…,n)。

1.3 评价精度分析

采用ROC 曲线[14]对3 种方案的LRM 结果进行检验。曲线下的面积AUC 用来表示预测准确性，AUC越高，预测精度值越高。

2 研究区及数据

2.1 研究区背景

研究区位处重庆市万州区和湖北省利川市，包含磨刀溪中下游及其支流龙驹河（图2a），坐标范围为108°30′E～108°45′E，30°30′N～30°40′N。地处四川盆地东缘，以江津至奉节沿齐岳山一线为界，平行展布北东向窄条状中低山脉、地势相对低凹的宽阔台地状山地和平缓丘陵（图2b）。

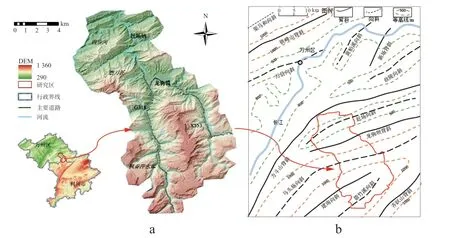
图2 研究区地理位置图和地质构造图

区内地层除背斜核部出露中生代三叠系外，其余均为侏罗系，主要为侏罗系中统上沙溪庙组（J2s上部以泥岩为主，中部粉砂质泥岩，下部厚层长石砂岩）、下沙溪庙组（J2xs泥岩、泥岩夹长石石英砂岩）和新田沟组（J2x顶部砂质泥岩，中部夹钙质砂岩），侏罗系下统自流井组（J1～2z页岩夹石英砂岩）、珍珠冲组（J1z中厚层石英砂岩、页岩）、以及三叠系上统须家河组（T3xj厚层长石石英砂岩夹页岩或煤层）和三叠系中统巴东组（T2b中厚～厚层含粉砂质灰岩夹钙质页岩）。

研究区崩塌共105 处，面积累计39.45×104 m2，体积累计321.89×104 m3。受地形地貌和岩土工程性质的影响，崩塌在上沙溪庙组密集发育，在其他地层相对较弱（图3a）。这种近水平地层内软硬岩互层的组合极易产生崩塌，严重威胁道路G318 和x553 的安全（图3b，3c）。

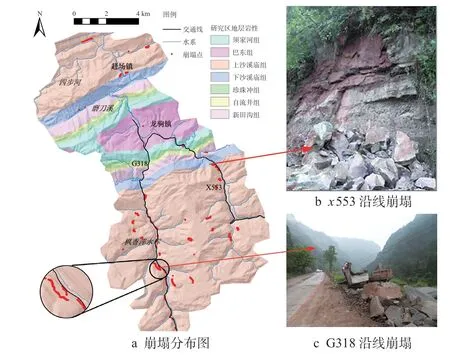
图3 崩塌分布图及典型崩塌

2.2 研究区数据源

基础数据:①Pleiades 影像数据（分辨率为0.5 m，影像时间:2 014.9.22）和高分一号数据（分辨率为1 m，影像时间:2015-03-30）；②地质图（1∶10 000）；③野外踏勘崩塌数据。

2.3 崩塌源区初步筛选

崩塌特征受高陡地形控制，为了锁定崩塌源区，利用最小坡度对区内栅格进行初步筛选。采用5°间隔将坡度分成16 类，通过统计各级内崩塌的比例，确定出其分布的最小坡度值。崩塌位于10°～70°内；在坡度达到25°时，崩塌数量陡增； 在40°时达到峰值（图4）。因此，选取25°为最小坡度。

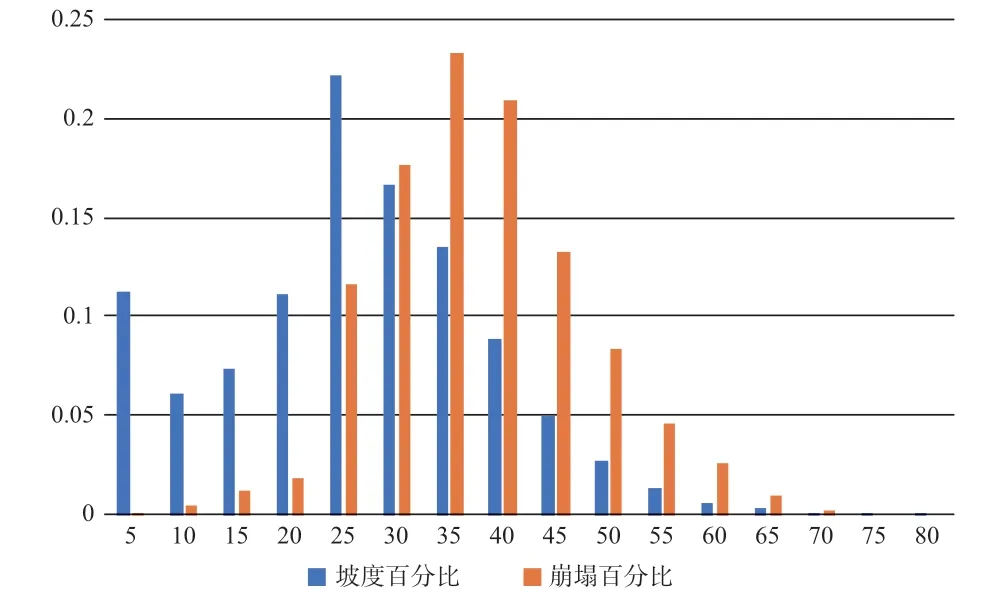
图4 崩塌源区与坡度范围对应图

2.4 因子预处理

通过对历史崩塌的发育特点与规律分析，选择10 个因子进行评价，各因子的取值情况见表1。

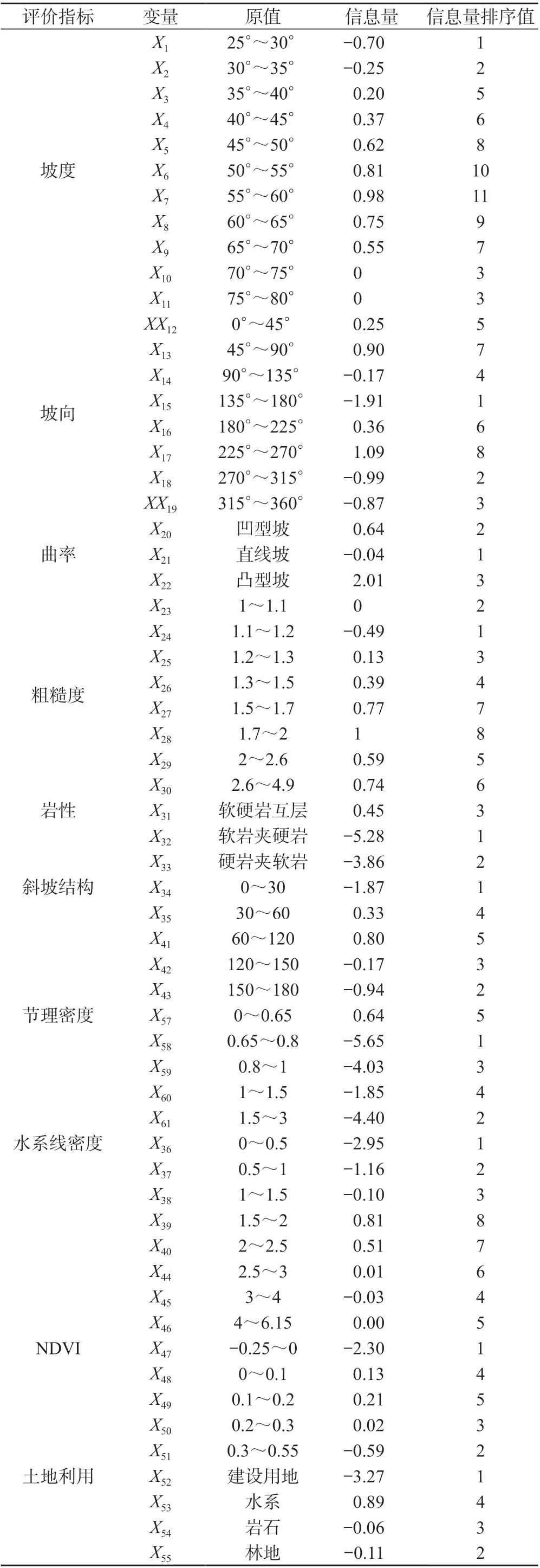
表1 崩塌源区评价变量分级表

1）地形地貌因子。坡度是控制崩塌重要因子，在较陡的斜坡带，应力集中，结构面发育时易崩塌，且岩石风化强度大，其属于连续型，通过等间距划分（图5a）。坡向控制不同坡面所受到的光照强度，其为连续型，通过等间距划分（图5b）。曲率反映斜坡坡面形态，其在空间几何上是斜坡表面上某个点的切线方向角所对弧长的转动率（图5c）。坡面形态反映斜坡的应力状态以及对地表水的汇聚能力，粗糙度反映坡体表面的起伏变化与侵蚀程度，定义为曲面面积与投影面积之比[16]。在GIS 中用自然间断法分级（图5d）。

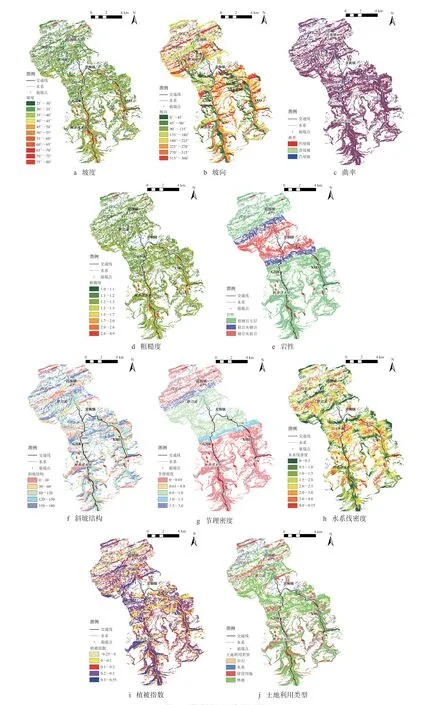
图5 崩塌源区评价因子图

2）工程地质因子。岩性分为三类:软硬岩互层（J2s,J2xs）、软岩夹硬岩（J1～2z,J2x）和硬岩含软弱夹层（T3xj,T2b,J1z），属于分类型（图5e）。斜坡结构反映结构面与临空面的空间关系，表征危岩体掉落概率大小。根据斜坡划分标准[17]分为5 类:顺向坡[0°～30°）、斜顺坡[30°～60°）、横向坡[60°～120°）、逆斜坡[120°～150°）及逆向坡[150°～180°]，其属于分类型（图5f），节理是崩塌重要控制因素，通过野外结构面测量获得，其为连续型，通过自然间断法分级（图5g）。

3）其他诱发因子。冲沟密度体现临空条件或反映水的侵蚀能力，属于连续型（图5h）。NDVI 反映地表植被的覆盖状况，良好的坡体稳定性更好。通过近红外和红外波段计算得到，属于连续型，通过等间距划分（图5i）。土地利用类型反映人类活动对斜坡的扰动情况。利用高分一号数据并采用波谱角分类（SAM）方法进行地物识别，得到土地利用类型图，其为分类型（图5j）。

3 结 果

3.1 崩塌源区空间分布特征

3 种变量取值方式在识别崩塌源极高易发区的能力上有差异。经过与信息量模型耦合后（方案2 中信息量值和方案3 中的信息量排序值）的评价，识别极高易发等级的崩塌源区的能力较原值的输入方式强（表2）。在原值方案下，研究区只有30%面积被判定为极高易发区；而在信息量值或者排序值的方案下，极高易发区的识别比例上升10%。

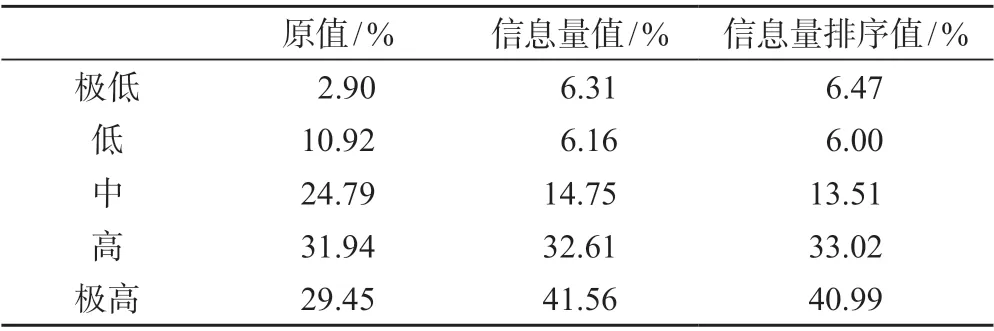
表2 不同变量取值方式下崩塌源易发区面积对比

图6a、6b、6c 结果表明，变量输入方式不会影响高易发区的分布情况，地质条件才是决定崩塌的重要因素。无论是哪一种输入方式，其崩塌源高易发区分布特征相同，即南北高，中部低。实质上，受地质构造和岩性的控制，主要分布在赶场向斜的北翼和马头场向斜的南翼（图3）的上沙溪庙组地层内。

3.2 崩塌源区识别精度检验与对比

变量的3 种取值方式在崩塌源识别精度上有差异（图6d）。通过比较ROC 曲线下AUC 值发现，采用信息量排序值作为变量的输入值得到的评价结果精度最高，达到0.855，其次是信息量值（0.832）和原值（0.821）的输入方案。进一步表明，在使用信息量模型与LRM 耦合评价崩塌源区易发性时，信息量排序值结果最优。从输入变量的特点分析其原因是:信息量值比原值数据更多包含了因子变量的权重值，而排序值相当于对信息量值大的因子赋予了二次权重，LRM 回归系数相当于三次权重，多权重的计算促使评价精度最优。该研究结果与樊芷吟[10]所得结论一致，即将信息量模型与LRM 耦合时，结果最优。

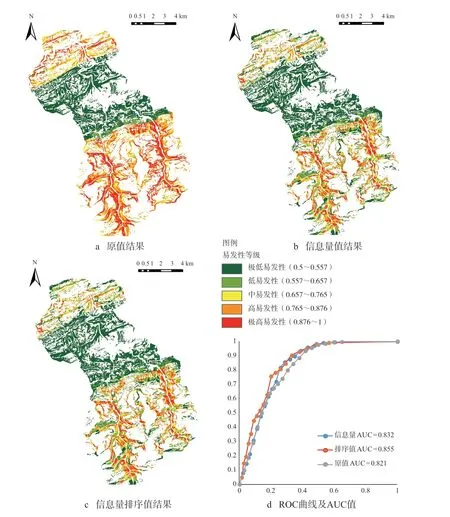
图6 研究区崩塌源区预测结果图和评价精度曲线图

4 结 语

针对变量存在多种输入方式从而影响崩塌源区识别精度的问题，以龙驹坝境内崩塌为例，讨论了变量的不同输入方式对崩塌源区预测的影响，所得结论如下:

1）崩塌源的分布受地形和地质条件控制，逻辑回归模型中变量的取值方式不会改变其总体空间分布特点，说明在评价地质灾害易发性工作中，灾害发育的地形、地质条件比模型重要。

2）3 种变量取值方式在崩塌源识别精度上有差异，以信息量排序值为取值方式能得到最高评价精度，同时，与信息量模型进行耦合能优化逻辑回归模型的预测结果，这与前人研究结论一致。

3）逻辑回归模型只是数学统计模型中的代表模型，变量取值方式对于其他预测模型是否有同样的精度提升的效果还需进一步研究。

4）案例研究区崩塌源总体处于坡度高于25°的斜坡带，各方案结果均表明极高和高易发区分布于赶场向斜的北翼和马头场向斜的南翼的上沙溪庙组地层内。