光纤位移传感器温度补偿的研究
2022-01-17李顶顶卢文科
李顶顶, 卢文科, 左 锋
(东华大学信息科学与技术学院,上海 201620)
0 引言
当前,随着科学技术的快速发展,传感器的种类不断增加,测量性能也不断提高。本文研究的光纤位移传感器,是一种以光信号形式传输被测量的新型传感器,具有损耗低、探头小、响应速度快、能实现非接触式测量等优点。其不仅能够有效地测量物体位移的变化量,而且在测量物体表面粗糙度[1]、液体的折射率[2]等方面也具有显著的优势,因此得到了广泛应用。
温度是影响传感器测量精度的一种主要干扰因素。在经典传感器中,主要采用结构对称的方法来消除其影响;在智能传感器的初级形式中,主要采用以硬件电路实现的“拼凑”补偿技术,但补偿效果仍然不能满足需要;在传感器与微处理器相结合的智能传感器系统中,主要采用监测补偿法[3]。本文利用温度传感器对光纤位移传感器的工作温度进行实时监测,利用粒子群算法优化最小二乘支持向量机(particle swarm optimization-least square support vector machine,PSO-LSSVM)模型进行温度补偿。
1 光纤位移传感器工作原理
光纤位移传感器按其工作原理可以分为功能型(传感型)传感器和非功能型(传光型)传感器两大类[4]。其中,非功能型传感器又可以细分为反射式、透射式、光纤微弯式3种。本文选取的反射式光纤位移传感器工作原理如图1所示。
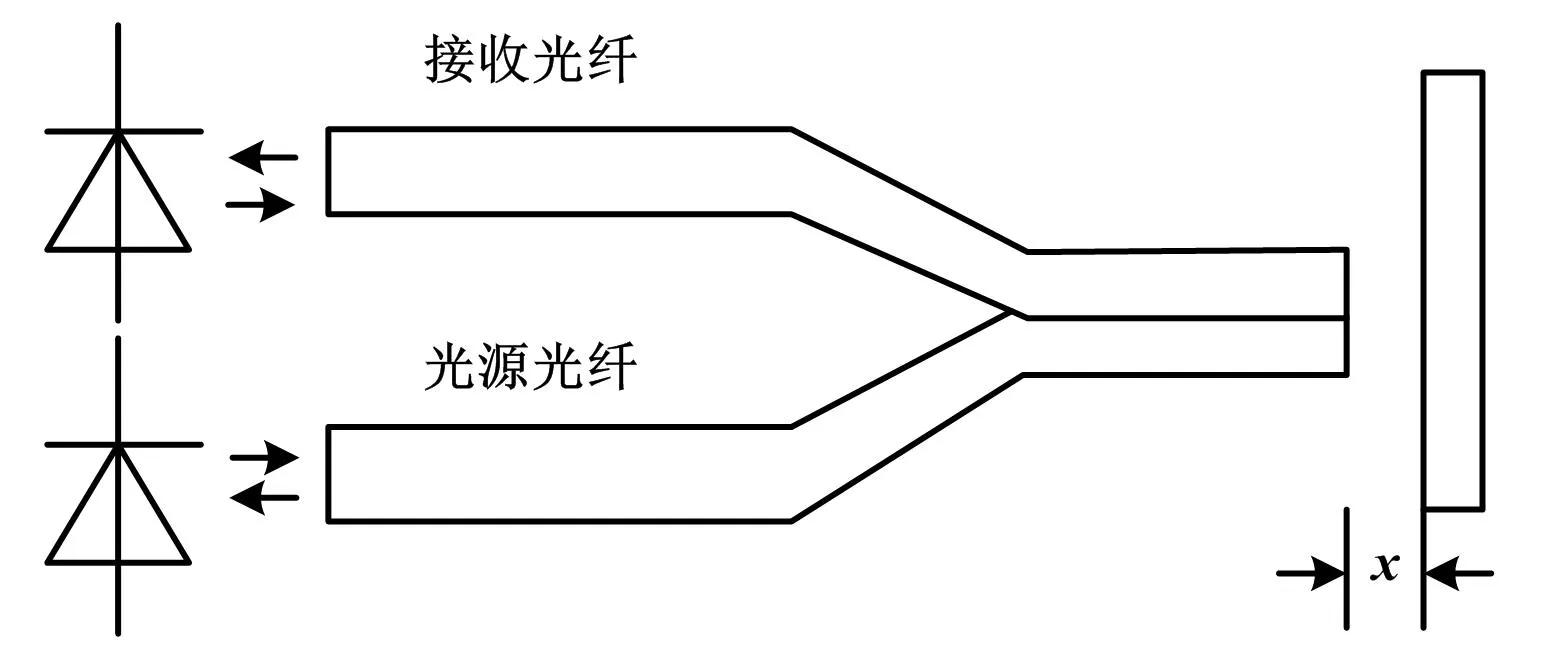
图1 反射式光纤位移传感器工作原理图Fig.1 Schematic diagram of reflective optical fiber displacement sensor
图1中,左侧端两支光纤分别作为光源光纤和接收光纤,在右侧端两支光纤合并组成光纤探头,呈现Y型结构。
从光源发射出的光在光源光纤中传输到反射片,经反射片反射的光射向接收光纤,在接收光纤中传输,最后由光电转换器接收。光电转换器接收到的光源强度与反射片表面材质、反射片到光纤探头的距离大小有关[5]。
由图1可知,当光纤探头贴紧反射片时,光电接收器接收到的光源强度为零;当光纤探头到反射片的距离不断拉大时,光电接收器接收到的光源强度也随之不断增大,并在达到峰值后又随着距离的增大而减小。其转折点在2 mm位移处左右。
2 PSO-LSSVM模型原理
2.1 粒子群优化算法的原理
粒子群优化(particle swarm optimization,PSO)算法是1种群智能算法,源于自然界鸟类寻找栖息地的群体行为,旨在对一特定的问题进行优化,从而找到最优解[6]。鸟类在被吸引飞向栖息地的过程中遵循3条简单规则,即:飞离最近的个体,以免碰撞;飞向目标;飞向群体的中心。起初,每只鸟都无特定目标地飞行。在这一过程中,每只鸟相互之间都进行信息共享,并更新自己的飞行位置和飞行速度,直到有一只鸟飞到栖息地。当设置期望栖息比期望留在鸟群中具有较大的适应值时,每只鸟都将离开群体而飞向栖息地,随后就自然地形成了鸟群[7]。
对粒子i在第j维子空间中运动的速度和位置,采用式(1)、式(2)进行更新:
vij(t+1)=vij(t)+c1r1j(t)[pij(t)-xij(t)]+
c2r2j(t)[pgj(t)-xij(t)]
(1)
xij(t+1)=xij(t)+vij(t+1)
(2)
式中:t为当前优化的代数;vij(t)、xij(t)分别为t时刻粒子i在j维子空间的速度、位置,i=1,2,...,M,M为该群体中粒子的总数;c1、c2为加速因子,通常在0~2之间取值;r1j、r2j为两个在0~1之间变化的相对独立的随机函数;pij(t)为粒子i的历史最好解(个体最优位置)的j维值;pgj(t)=min{pij(t)}为所有粒子在t时刻的历史最好解(群体最优位置)的j维值。
式(1)中:第二项是粒子i从当前位置向自身历史最优位置移动的调整分量;第三项是粒子i从当前位置向群体历史最优位置移动的调整分量。由此可见,粒子下一时刻的运动速度受自身当前位置、自身历史最优位置、群体历史最优位置的影响。
迭代次数是预先设定好的。在每次迭代过程中,当前粒子最优位置和群体最优位置都是根据每个粒子的适应值来确定的。适应值则通常是根据以均方误差来表示的目标函数计算出来的。
当迭代次数达到设定值或者群体目前搜索到的最优位置满足预设最小适应值时,迭代结束[8]。
2.2 最小二乘支持向量机算法的原理
支持向量机(support vector machines,SVM)的基本思想是将输入空间通过非线性变换的方法变换到一个高维特征空间。在这个高维特征空间中,利用线性判别函数来寻找输入空间的一种非线性关系,能够解决样本容量小的问题、避免局部极值问题、处理输入空间非线性问题和解决维数问题,从而达到很好的优化效果[9]。
在特征空间中,支持向量机通过以下线性回归函数进行数据的分类和拟合。
f(x)=ωK(x,x′i)T+b
(3)
式中:x′i为支持向量机的支持向量;K(x,x′i)为支持向量机的核函数,可实现从输入空间到特征空间的非线性变换。
本文的核函数采用高斯径向基函数(radial basis function,RBF)核,如式(4)所示:
(4)
式中:δ为核函数参数,是本文需要优化的一个参数。
最小二乘支持向量机(least square support vector machine,LSSVM)是基于标准的支持向量机发展而来的。两者的区别在于LSSVM将不等式约束改为等式约束,优化目标的损失函数为误差的平方和[10]。
优化问题表示为:
(5)
式中:C为惩罚因子,是本文需要优化的另一个参数;ξi为松弛因子。
约束条件为:
yi=〈ω,x〉+b+ξi
(6)
式中:i=1,2,…,l。
引入拉格朗日函数,最终可得到LSSVM的回归方程,如式(7)所示:
(7)
2.3 PSO-LSSVM模型的实现
PSO-LSSVM模型的核心思想是利用PSO算法对LSSVM算法中的C和δ进行优化选取,以提高模型的优化效果[11]。
首先,对PSO算法中的参数以及适应度值进行初始化。适应度函数设置为预测值与期望值的均方差。接着,根据PSO算法每次迭代确定的C和δ值,求出预测值和适应度值。最后,不断地根据适应度值调整粒子群的局部最优位置和全局最优位置。即对于每个粒子:若其适应度值比它的历史最优适应度值还小,则更新局部最优位置;若其适应度值比历史全局最优适应度值还小,则更新全局最优位置,直至迭代次数达到设定值,算法结束。此时的C和δ为最优取值,相应的预测值即为温度补偿后的结果[12]。
PSO-LSSVM算法流程如图2所示。

图2 PSO-LSSVM算法流程图Fig.2 Flowchart of PSO-LSSVM algorithm
3 温度补偿的实现
3.1 二维标定试验
PSO-LSSVM模型的光纤位移传感器温度补偿系统如图3所示。
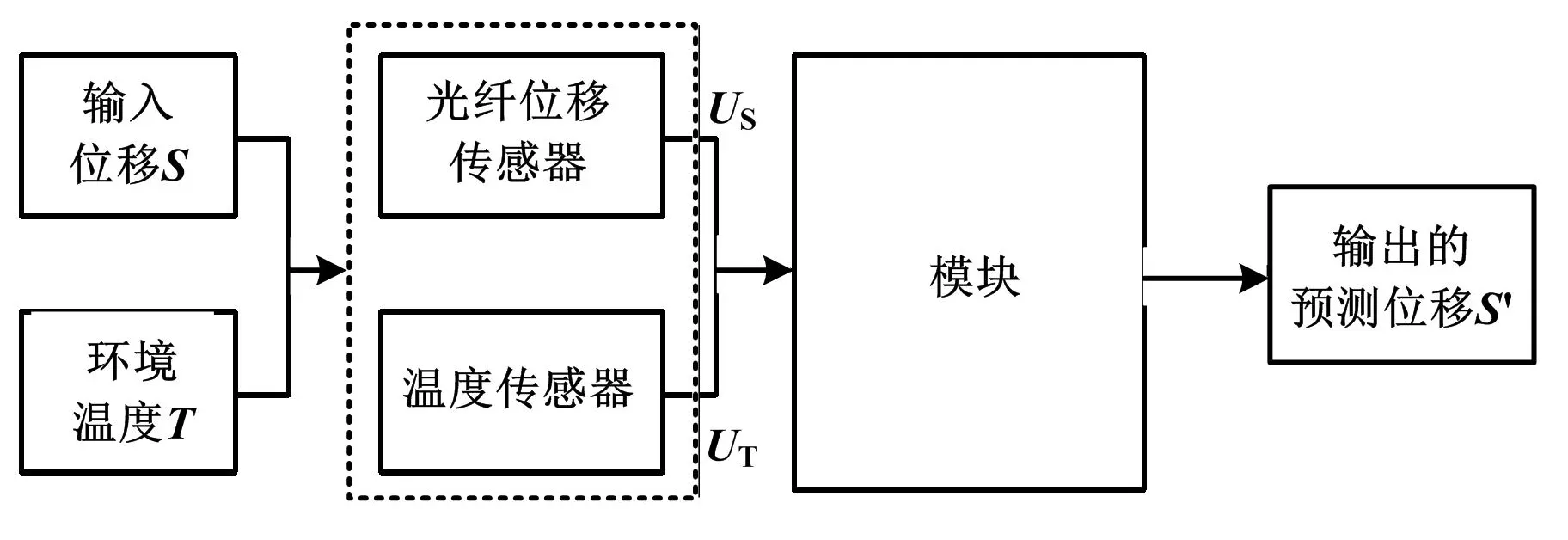
图3 光纤位移传感器温度补偿系统框图Fig.3 Block diagram of optical fiber displacement sensor temperature compensation
为了研究温度对位移特性的影响,需要测量不同温度下光纤位移传感器的输出量。本文选取22.4 ℃、25.0 ℃、28.1 ℃、31.6 ℃、35.5 ℃、38.2 ℃、42.7 ℃、46.9 ℃作为8个温度标定点,选取的位移区间为0.1~1.7 mm,分为0.1 mm、0.3 mm、0.5 mm、0.7 mm、0.79 mm、0.9 mm、1.1 mm、1.3 mm、1.5 mm、1.7 mm 这10个位移测量点。
需要用到的试验器材为LM35温度传感器、反射式光纤位移传感器、THSRZ-2型传感器系统综合试验装置和恒温箱。测量得到的光纤位移传感器二维标定试验数据如表1所示。

表1 光纤位移传感器二维标定试验数据Tab.1 Two-dimensional calibration experiment data of optical fiber displacement sensor
由表1可知,光纤位移传感器的输出明显受温度变化的影响。这里选用零位温度系数α0和灵敏度温度系数αs作为温度对光纤位移传感器测量精度影响的衡量标准。
零位温度系数表示零位输出值随温度漂移的速度,由表1数据可求得:

(8)
式中:ΔU0m为零位时最大输出电压值与最小电压值之差;ΔT为工作温度变化范围;UFS为光纤位移传感器满量程时的最大输出电压值。
灵敏度温度系数表示的是传感器灵敏度随温度漂移的速度,由表1数据可求得:
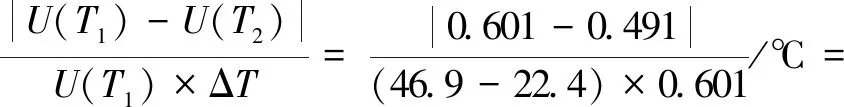
(9)
式中:|U(T1)-U(T2)|为满量程下的最大变化量;ΔT为工作温度为T1、T2时,全量程范围内的同一位移输入条件下的输出电压最大值与最小值之差。
3.2 温度补偿结果分析
使用MATLAB对本文设计的PSO-LSSVM温度补偿模型进行仿真。设置粒子群的维数为2,C1=1.7,C2=1.7,粒子个数为30,迭代次数为500。
选择工作温度为22.4 ℃、28.1 ℃、35.5 ℃以及32.7 ℃时的4组数据作为训练样本,剩余4组作为测试样本。将数据作归一化处理,经过PSO-LSSVM算法模型处理后反归一化。由此得到的温度补偿后的预测位移值如表2所示。

表2 温度补偿后的预测位移值Tab.2 Predicted displacement value after temperature compensation
由表2可得,温度补偿后的零位温度系数α′0和灵敏度温度系数α′s分别为:

(10)
(11)
由温度补偿前后的零位温度系数和灵敏度温度系数比较可得:零位温度系数从9.78×10-3/℃提升到2.07×10-3/℃;灵敏度温度系数从7.47×10-3/℃提升到1.51×10-3/℃,取得了较好的补偿效果。
PSO-LSSVM算法模型得到的惩罚因子C=1 000,核函数参数σ=1.847 2,预测结果的均方误差为7.081 6×10-4。其适应度曲线如图4所示。
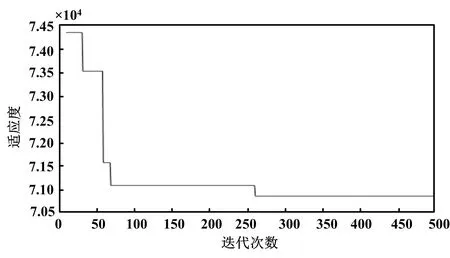
图4 适应度曲线Fig.4 Fitness curve
由图4可知,当迭代次数为255时,适应度达到最小,即输出的预测位移值最接近期望值。
根据表2温度补偿后的数据作出拟合效果图,如图5所示。

图5 温度补偿后的数据拟合效果图Fig.5 Data fitting effect diagram after temperature compensation
由图5可以看到,温度补偿后的8组数据基本上拟合在了一条直线上,再次证明PSO-LSSVM算法模型取得了较好的补偿效果。
4 结论
本文针对光纤位移传感器的温度漂移现象,提出了一种PSO-LSSVM算法模型,对传感器进行温度补偿。通过对温度补偿前后的数据比较,零位温度系数从9.78×10-3/℃提升到2.07×10-3/℃;灵敏度温度系数从7.47×10-3/℃提升到1.51×10-3/℃。由此表明,PSO-LSSVM算法模型能够有效地实现温度补偿。
