基于LSTM的飞灰含碳量预测
2022-01-17河北建投任丘热电有限责任公司刘四辈
河北建投任丘热电有限责任公司 李 奔 薛 峰 刘四辈
1 引言
飞灰含碳量是反映电厂燃煤锅炉效率及经济性的重要指标之一。飞灰含碳量的准确测量是提高锅炉运行过程的热转化效率、降低发电煤耗的基础。目前,飞灰含碳量测量方法主要分为物理测量和软测量两大类。主流的物理测量方法中,传统的燃烧失重法准确性高,适用性广但是取样间隔长、时滞性大,难以及时反映锅炉燃烧情况;热重分析法自动化程度高、准确度高,但是分析时间长,设备昂贵;微波法测量速度快、精度高、仪器简单,但是难以适应火电厂煤质多变情况,测量腔易堵灰[1]。其它物理测量方法也都面临延时性、准确性、价格方面的问题,难以做到飞灰含碳量的实时测量。
软测量技术是利用一些易于实时测量的,与被测量密切相关的变量,通过在线分析来估计难以测量的实时值,为飞灰含碳量测量提供了方法。在飞灰含碳量软测量方面,多采用支持向量机(SVM)构建软测量模型:基于数据相似度加权因子的最小二乘支持向量机(LSSVM)软测量模型,利用双种群差分进化算法优化模型参数的选取,通过在线评估和递推矫正实现模型的自适应矫正[2];万有引力搜索算法(GSA)与LSSVM 算法相结合的GSA-LSSVM 飞灰含碳量预测模型[3];利用主成分分析的方法优化了LSSVM 模型的输入参数[4];在计算样本特征距离的基础上,融合密度和离散度构建全局代表性指标,完成样本的稀疏化,降低了LSSVM 模型的计算规模的同时提高了模型精度[5];采用交叉验证法[6]、粒子群[7]优化了SVM 模型的主要参数,并验证了模型的准确性;采用粒子群和支持向量回归法构建了飞灰含碳量测量模型[8];基于LSSVM 飞灰含碳量测量装置[9-10]。支持向量机的优势在于具有较强的非线性映射能力,并且具有明确的数学理论支持,但是在处理多特征大规模的样本时会耗费大量机器内存和运算时间,难以保证时效性。除支持向量机外,具有高纬非线性拟合能力的神经网络在预测飞灰含碳量方面同样得到了广泛应用。文献提出一种基于互信息选择的神经网络飞灰含碳量预测模型,并通过PLC 硬件实现[11]。还有基于蚁群算法优化的BP 神经网络模型预测飞灰含碳量,和燃煤锅炉飞灰含碳量的BP 神经网络模型。
支持向量机、BP 神经网络虽然具有较好的非线性映射能力,但是算法研究的对象是某一时刻的操作参数与对应时刻的飞灰含碳量。而瞬时的飞灰含碳量是一段时间内操作的综合结果,用瞬时的操作对飞灰含碳量进行拟合更适用于稳态工况,难以满足飞灰含碳量的动态测量要求。本文利用长短期记忆网络(LSTM)结合灰色关联算法构建飞灰含碳量预测模型,为飞灰含碳量动态测量提供优化方案。
2 参数选择
2.1 数据筛选
本文使用的数据为某热电厂350MW 机组实际运行数据。该电厂采用实验方法测量飞灰含碳量,每天测量两次,实测数据具有较高的准确性。选取机组一年的运行数据,参考电厂超温超限、环保性要求,以主蒸汽温度、SO2排放量、NOx 排放量等参数为筛选条件,除去不符合电厂安全环保要求对应的时间标签的样本数据。以早晚两次飞灰含碳量取样时间为节点,按时间标签取主要相关参数的前半小时运行数据作为样本数据。其中,主要相关参数数据由现场DCS 系统中直接取出,飞灰含碳量由现场实测数据录入。主要参数及测点名称如表1所示:
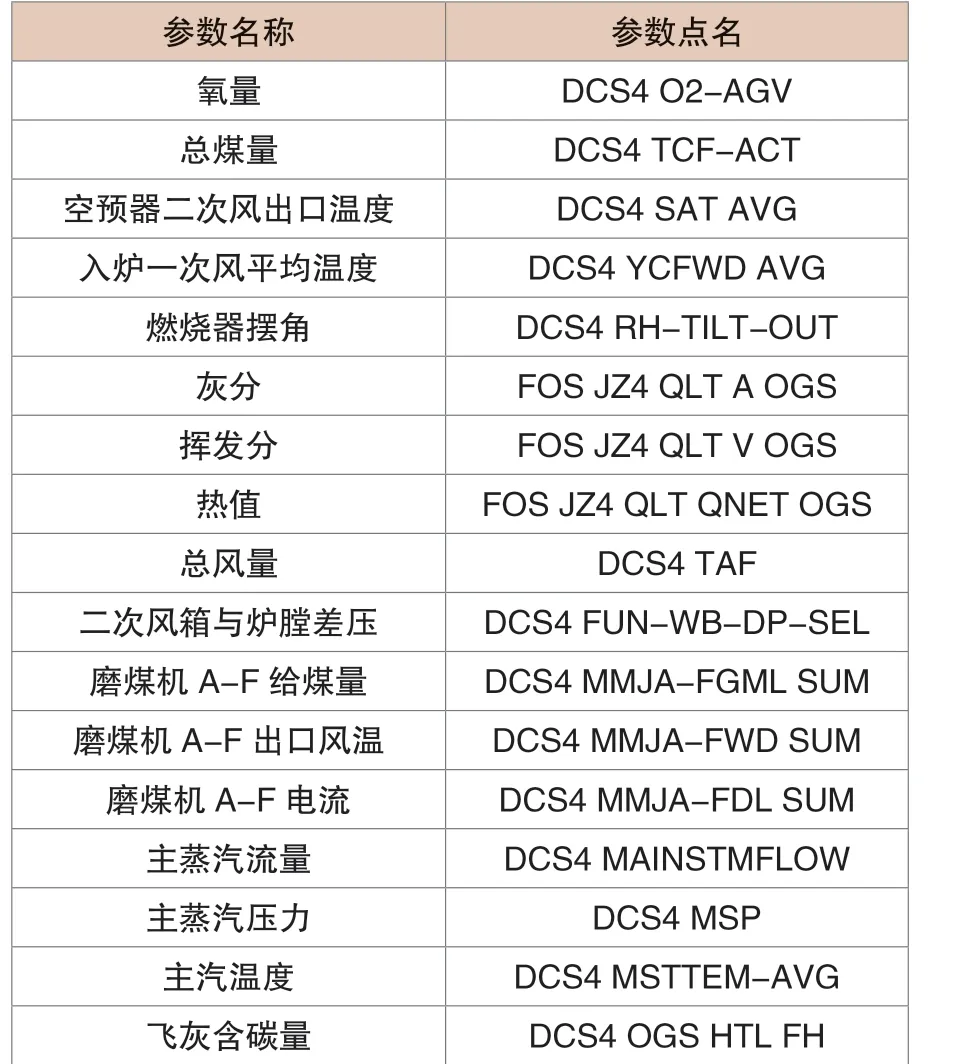
表1 主要参数及测点
2.2 飞灰含碳量影响因素分析
根据理论分析及现场实际调研,选用锅炉汽水系统中的主蒸汽温度、主蒸汽压力、主蒸汽流量,风烟系统中的总风量、入炉一次风温度、空预器出口二次风温度、二次风箱与炉膛差压、燃烧器摆角,制粉系统中的总煤量、煤质参数、磨煤机给煤量、电流等参数与飞灰含碳量进行相关性分析。采用斯皮尔曼等级相关系数,即spearman 相关系数进行相关性计算分析,该系数计算公式为:

将飞灰含碳量与每一个参数进行相关性分析计算,结果如图1所示。
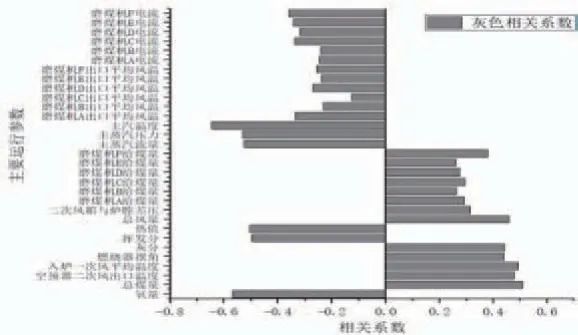
图1 飞灰含碳量相关性因素分析
从相关性分析结果来看,汽水系统中选取的参数均与飞灰含碳量有较强的相关性。主蒸汽温度与飞灰含碳量的关联性最强。主蒸汽温度主要受燃烧强度的影响,主蒸汽温度越高,燃烧强度越大,燃尽情况越好飞灰含碳量越低。与主蒸汽温度类似,主蒸汽压力、流量等与锅炉燃烧状态直接相关的状态参数与飞灰含碳量也有较强的相关性。
风烟系统中烟气含氧量是评价炉内燃烧情况的重要指标,表征了炉内的氧化还原气氛,含氧量越高煤粉燃尽越充分。总风量、二次风箱与炉膛差压表征了炉内总配风量及二次风配风大小,在影响炉内燃烧气氛的同时也影响了烟气带出热量的多少,与飞灰含碳量具有较强的相关性。入炉一次风平均温度体现了煤粉流在燃烧初期携带的热量,影响煤粉的初期燃烧情况。一次风温的大小取决于入炉煤的煤种,对于难燃的无烟煤、贫煤等一般采用较高的一次风温,而此类煤种燃尽情况较差,从总体趋势上呈现出一次风温越高,燃尽情况越差的趋势。燃烧器摆角决定了炉内火焰的基本形状,进而影响燃烧状况,影响飞灰含碳量。
制粉系统中,表征煤质信息的参数直接影响了煤粉的燃烧过程,其中热值表征了入炉煤在炉膛内释放的热量,对燃烧强度起决定性作用,但是热值越高的煤种煤化程度越高,通常燃烧特性较差,着火温度要求高,燃尽困难。而挥发分较高的煤种燃烧特性好,易于燃尽。灰分不参与燃烧并且在燃烧过程中会吸收热量,导致炉膛温度降低,进而导致燃尽程度降低,飞灰含碳量升高。总煤量在总体趋势上体现了锅炉带负荷的情况,总煤量越大炉内燃烧强度越高,燃烬情况越好。与总煤量类似的各层磨煤机给煤量对燃烬情况也具有较强的影响,同时呈现上下层磨煤机影响较大,中间层影响较小的趋势。磨煤机电流一定程度上表征了磨煤机的出力情况,影响煤粉细度,与飞灰含碳量具有较强的相关性。
根据灰色相关性分析结果,最终选定氧量、总煤量、空预器二次风出口温度、入炉一次风平均温度、燃烧器摆角、灰分、挥发分、热值、总风量、主蒸汽流量、主蒸汽压力、主蒸汽温度作为模型输入参数,构建飞灰软测量模型。
3 飞灰含碳量预测模型
3.1 长短期记忆网络简介
长短期记忆网络(LSTM)是在循环神经网络(RNN)的基础上提出的时序神经网络算法。与传统神经网络不同,在RNN 神经网络中,一个序列当前的输出与之前的输出也有联系。具体表现为网络会对前面的信息进行记忆并应用于当前输出的计算中,即隐含层之间的节点互相连接,并且隐含层的输入包括输入层的输出与上一时刻隐含层的输出。但是循环神经网络无法解决长时依赖问题。针对这一问题LSTM 在RNN 的基础上增加了遗忘门、信息增加门、输出门的概念,实现长期记忆功能。在LSTM 算法中,将各种门控的结果称为细胞记忆,细胞记忆的更新过程就是LSTM 算法训练的过程,由各种门层的结构决定。
LSTM 算法中,遗忘门用于决定从上一时刻的细胞状态中丢弃哪些信息。本文中选择sigmoid 函数作为遗忘门ft的激活函数,记为σ,则忘记门表达式为:

其中Wf为遗忘门的权值,bf为偏置值,ht-1为上一时刻的隐藏状态。
信息增加门中,包括输入门层it和候选值向量选两值部向分量,为输备入选门的层更it新决内定容哪。些本信文息中需选要择更σ新,作候为的激活函数,tanh 函数作为的激活函数,则对应的表达式为:

利用遗忘门和信息增加们对细胞状态Ct进行更新:
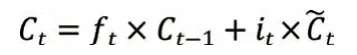
输出门中,包括输出ot和t 时刻的隐藏状态ht,表达式为:

对于每一时刻,采用梯度下降法(backpropagation through time,BPTT)进行网络的反向传播,假设该时刻网络的第k 个输出参数为ok,该输出参数的实际值为yk,则总误差E 的计算公式为:

则采用梯度下降法对LSTM 网络各层权值更新的计算公式为:
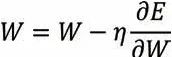
3.2 基于LSTM 的飞灰含碳量预测模型
采 用TensorFlow-2.2构 建LSTM 网 络,对飞灰含碳量进行预测模型建模。建模使用该厂350MW 机组2020年1月至12月的实际运行数据。模型中选用sigmoid 函数作为遗忘门、输入门层的激活函数,选用tanh 函数作为候选值向量、细胞状态的激活函数。选用均方误差作为模型的损失函数,选用平均误差作为评价预测误差的标准。模型实现过程如下:
根据电厂各系统之间的耦合关系及现场调研结果,初步选定与飞灰含碳量相关的参数;以飞灰取样时间为基准,按时间标签向前取半小时主要影响参数的运行数据作为时序样本数据,对样本数据进行稳定性、环保性、安全性筛选;采用灰色关联分析模型,计算出相关参数与飞灰含碳量的关联系数,并对参数进行筛选,得到影响飞灰含碳量的主要参数的时序样本数据;采用Kera3.0构建基于LSTM神经网络的飞灰含碳量测量模型:
初始化网格,设置双层隐含层结构、损失函数、对应层的激活函数、初始化各层权值、设置初始超参数;按照时间标签对时序样本数据进行处理,将相同时间段内的数据与对应的飞灰含碳量测量值作为一组样本,按照6:2:2的比例将样本组划分为训练集、验证集和测试集;利用训练集和验证集对网络进行训练,并根据训练结果调整网格结构和超参数;利用测试集数据验证模型的有效性与准确性。
3.3 模型训练结果
取该厂2019年全年的运行数据的4/5作为训练集用于模型训练。采用交叉验证法,将训练集分为5个子集,每个子集均做一次测试集,其余的作为训练集,进行交叉验证。模型优化器选择综合性能较好的Adam 优化器,在学习率0.01、一阶矩估计的指数衰减0.9,二阶矩估计的指数衰减率0.99的情况下,以均方误差作为模型的损失函数,对模型进行500次训练,训练结果显示初始阶段损失函数值下降较快,之后在震荡中持续下降,最终在250次训练后趋于稳定。此时飞灰含碳量的均方误差为0.0038168,平均训练误差为4.17%,符合现场应用的精度要求。
4 预测模型效果验证
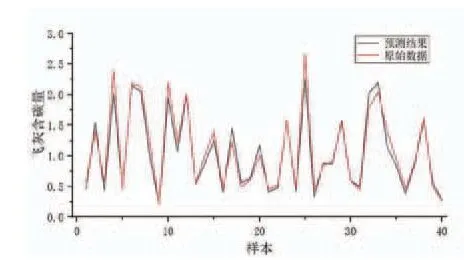
图2 LSTM 飞灰含碳量预测结果比对
从测试数据集中随机选取50组数据,验证模型预测效果,结果如图3所示。从图中可以看出,预测结果与实际测量结果吻合较好。预测样本误差如图4、图5所示,其中相对误差均值为9.85%,最大相对误差为23.995%,绝对误差绝对值的均值为0.104,最大为0.4126,证明软测量模型具有较好的预测效果。
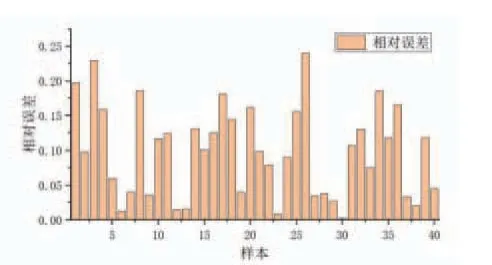
图3 LSTM 飞灰含碳量预测相对误差

图4 LSTM 飞灰含碳量预测绝对误差
