轮毂直驱空气悬架系统垂向动力学特性分析

2022-01-17李仲兴宋鑫炎薛红涛

江苏大学学报（自然科学版） 2022年1期

李仲兴，陈鑫，宋鑫炎，薛红涛

(江苏大学汽车与交通工程学院，江苏镇江 212013)

随着《“十三五”国家科技创新规划》和《汽车产业中长期发展规划》的推进，推动“纯电驱动”技术转型，加快新能源汽车研发成为汽车发展的主要方向.轮毂直驱电动汽车作为电动汽车驱动形式之一，具有控制灵活、传动高效、结构紧凑等优点，可有效降低车辆能耗[1]、提高整车的主动安全性[2].但轮毂电动机的应用加剧了簧下部件的振动，并加入了额外的高频激励源，尤其是在轮毂电动机运行过程中，因气隙不均会导致电动机产生不平衡电磁力[3-4].针对簧下质量增大的问题，童炜等[5]以参数匹配为目的，分析了簧下质量与电动机质量比、阻尼比等参数对车辆振动的影响.针对电动机不良振动问题，A.KULKARNI等[6]分析了电动机振动对悬架的影响.然而，针对轮毂直驱电动汽车簧下质量增大和电动机不平衡电磁力2大问题，在悬架参数变化时的系统特性研究却很少见.这对轮毂直驱悬架系统控制研究的深入开展造成了一定的困难.

空气悬架是一种典型的半主动悬架，具有低振动频率和良好的隔振性能，并具有诸多的衍生结构.其中带附加气室的空气悬架可实现调节空气弹簧刚度的作用，在提升车辆乘坐舒适性和操纵稳定性方面具有独特的优势[7].

笔者将轮毂直驱系统和空气悬架系统2个相对独立的系统进行整合，构建轮毂直驱空气悬架(hub direct drive air suspension,HDD-AS)系统，通过动力学模型研究路面随机激励与电动机不平衡电磁力耦合作用下轮毂电动机与空气悬架垂向振动性能，分析电动机偏心距、簧上质量加速度、悬架动行程、轮胎动载荷和簧下质量加速度在悬架参数改变时的时频特性.

1 1/4HDD-AS系统模型

1.1 永磁无刷直流电动机模型

根据试验电动机的结构与参数，建立极对数为23，槽数为51的永磁无刷直流电动机模型作为轮毂电动机模型，其额定功率为4 kW，额定电压为72 V，电压方程为

(1)

式中：ua、ub、uc分别为a、b、c三相电压；Rm为相电阻；ia、ib、ic分别为a、b、c三相电流；L为绕组自感；M为绕组互感；pd为微分算子；ea、eb、ec分别为a、b、c三相反电动势.

(2)

式中：kea、keb、kec分别为a、b、c三相的反电动势系数；ω为转子角速度.

电动机电磁转矩方程和电动机机械运动方程分别为

(3)

(4)

式中：Te为电磁转矩；Jm为电动机转动惯量；μ为摩擦因数；TL为电动机负载转矩.

1.2 不平衡电磁力

不考虑永磁体布置不对称及电枢绕组设计不合理等问题，在随机路面激励下，外转子永磁无刷直流电动机定转子产生偏心，引发电动机气隙不均，导致气隙磁场的畸变，从而产生不平衡电磁力.

气隙磁场包括永磁体磁场和电枢反应磁场，忽略了饱和与漏磁效应后，运用线性叠加法将二者相加，获得电动机径向气隙磁场与电动机切向气隙磁场，结合由偏心距计算的磁导修正系数，计算电动机偏心状态下的不平衡电磁力.

假设永磁体磁化强度均匀，铁芯磁导率无穷大，永磁体充磁方向为径向充磁.径向气隙磁场Ber和切向气隙磁场Bet计算方法[8]如下：

Ber(r,α,t)=(Bmr(r,α,t)+Bar(r,α,t))εδ，

(5)

Bet(r,α,t)=(Bmt(r,α,t)+Bat(r,α,t))εδ，

(6)

式中：r为极坐标系极径；α为极坐标系极角；Bmr为永磁体径向磁场；Bar为电枢反应径向磁场；Bmt为永磁体切向磁场；Bat为电枢反应切向磁场；εδ为磁导修正系数.

由于电动机定转子间存在偏心而产生的垂向不平衡电磁力Fez与纵向不平衡电磁力Fex计算如下：

sinα+2Ber(r,α,t)Bet(r,α,t)cosα]dα，

(7)

cosα-2Ber(r,α,t)Bet(r,α,t)sinα]dα，

(8)

式中：ld为电动机轴向长度，ld=0.06 m；μ0为真空磁导率.

1.3 带附加气室空气弹簧数学模型

带附加气室空气弹簧由空气弹簧、连接管路、附加气室和电磁阀组成.将空气弹簧视为变质量开口绝热系统，其内部气体状态方程为

(9)

式中：p、p0分别为空气弹簧瞬时气压和空气弹簧初始气压；V、V0分别为空气弹簧瞬时体积和初始体积；m、m0为空气弹簧瞬时气体质量和初始气体质量；k为等熵指数；const为常数.

当气体流经连接管路时，气体被压缩，因此管路的实际通流能力取决于气体压缩后的最小面积，意味着气体交换时存在着节流效应.同时，因管路具有一定长度，气体交换存在时滞效应.

考虑连接管路节流效应，管路中流经的气体质量流量[9]为

(10)

式中：t为时间;Se为有效通流面积，Se=0.000 2 m2；λt为管路的阻力系数；Tup为气压为pmax端的气体温度;pmax为管路上游气体气压；pmin为管路下游气体气压.

考虑管路时滞效应，管路中不同位置处的质量流量为

(11)

式中：R为气体常数；Tdn为气压为pmin端的气体温度；l为连接管路长度，l=0.8 m;c为声速.

附加气室在运行过程中为变质量开口绝热定容系统，其数学模型[10]为

(12)

式中：pn为附加气室内气体压力；mn为附加气室内气体质量；constn为常数.

1.4 三质量系统模型

轮毂电动机结构如图1所示.三质量系统模型如图2所示.

图1 轮毂电动机结构

图2 三质量系统模型

以轮毂电动机气隙为分界面，拆分电动机内定子与外转子，将传统的1/4整车二自由度振动模型转化为1/4整车三自由度振动模型.三质量系统振动微分方程[11]为

(13)

式中：ms为簧上质量，ms=337.5 kg；zs为簧上质量垂向位移；Fa为空气弹簧力；cs为阻尼减振器阻尼系数；mur为轮胎与电动机转子质量，mur=66.5 kg;mus为电动机定子与剩余簧下质量，mus=57.5 kg;zur、zus分别为mur、mus的垂向位移；kb为轴承刚度，kb=5×10-6N·m-1；kt为轮胎刚度，kt=250 kN·m-1；q为随机路面输入；Fez为垂向不平衡电磁力.

空气弹簧力为

Fa=(p-pa)Aa-msg，

(14)

式中：pa为大气压；Aa为空气弹簧有效面积；g为重力加速度.

电动机定转子间偏心距为

e=zus-zur.

(15)

以电动机定转子间偏心距与不平衡电磁力为纽带，构建成轮毂电动机与空气悬架耦合模型.HDD-AS系统模型结构如图3所示，其中：fd为悬架动行程；n为电动机转速；vref为参考车速.

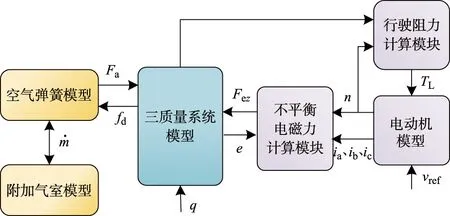
图3 HDD-AS系统模型结构

参考滚动阻力计算方法，计算1/4HDD-AS系统实时滚动阻力，作为电动机运行负载转矩.滚动阻力为

Ff=(ms+mus+mur)g(7.6×10-3+5.6×10-5v)，

(16)

式中：v为车速.

2 试验验证

基于INSTRON 8800单通道电液伺服系统、LMS SCADAS Mobile数据采集系统和知豆D1车载电动机控制器，搭建试验台架,试验设备如图4所示.

图4 试验设备

试验台簧上质量以一根横梁代替，横梁下方为弹簧与阻尼减振器.阻尼减振器另一端与摆臂中部连接，连接处可产生相对滑动，阻尼减振器与摆臂中部间装有HD-YB-11LY型轮辐式拉压力传感器.摆臂与立柱采用螺栓铰接，因此摆臂可上下进行摆动.摆臂末端为轮毂电动机与车轮，并设计有一方形平台，用于搭载加速度传感器.车轮置于双滚筒上，接受单通道液压激振台所施加的激励.

根据试验台架结构与参数，搭建试验模型.该试验模型中簧上质量位移锁死，悬架也为被动悬架，用以模拟试验实况，便于比对试验与仿真结果.

试验台架如图5所示.试验时，首先上升液压激振台，当拉压力传感器所采集的压力信号达到预定值(该预定值用于模拟车身垂向载荷)，启动轮毂电动机，将其转速提升至100 r·min-1.随后利用单通道液压伺服系统施加频率为2 Hz，幅值为0.003 m的正弦激励，采集轮毂电动机相电流信号和簧下质量加速度信号，与同等工况下的仿真结果对比，电动机相电流试验与仿真结果对比如图6所示，簧下质量加速度频域试验与仿真结果对比如图7所示，其中f为频率.

图5 试验台架

图6 电动机相电流对比

图7 簧下质量加速度频域对比

从图6可以看出：试验与仿真的电流周期相同，信号特征相符.从图7可以看出：试验与仿真的簧下质量加速度频域成分大致相同；仿真中悬架振动产生的低频峰值所在频域和电动机振动所产生的高频峰值所在频域与试验所得相同.这说明所搭建的轮毂电动机和电动机不平衡电磁力模型在悬架力与路面激励共同作用下贴近实际情况，可以较为精准地反映路面随机激励下电动机因气隙不均所产生的不平衡电磁力.在此基础上，结合带附加气室空气悬架模型，在随机路面激励与电动机不平衡电磁力耦合作用下，开展HDD-AS系统特性研究.

3 1/4HDD-AS系统性能分析

选取C级路面，路面的不平度系数Gq(n0)=2.56×10-4m3，参考空间频率n0=0.1 m-1，车速为40 km·h-1.

3.1 HDD-AS系统响应均方根值分析

带附加气室空气弹簧具有改变弹簧刚度的能力.通过开启附加气室电磁阀，连通附加气室与空气弹簧，改变气体动态特性，达到改变空气弹簧刚度的效果.空气弹簧动刚度k1随附加气室容积的变化曲线如图8所示，改变附加气室容积，空气弹簧动刚度发生相应变化；附加气室容积Vf在1、2、3 L时空气弹簧动刚度下降明显，之后随着附加气室容积的变大，空气弹簧动刚度基本不变.

图8 空气弹簧动刚度随附加气室容积的变化曲线

附加气室容积与阻尼系数改变时电动机偏心距、电动机不平衡电磁力、簧上质量加速度、悬架动行程、轮胎动载荷Fd、簧下质量加速度均方根值响应曲线如图9所示，其中‖·‖rms为均方根值.

图9 HDD-AS系统参数均方根值响应曲线

从图9可以看出：在路面激励与电动机不平衡电磁力耦合作用下，电动机偏心距、电动机不平衡电磁力、悬架动行程、轮胎动载荷以及簧下质量加速度随阻尼系数的变化趋势一致，即随阻尼系数的增大而减小；簧上质量加速度随阻尼系数增大而增大.由此可知，增大阻尼系数可抑制电动机偏心，降低不平衡电磁力，并减小悬架动行程、轮胎动载荷及簧下质量加速度，但会使簧上质量加速度增大.

从图9还可以看出：电动机偏心距、电动机不平衡电磁力以及轮胎动载荷随附加气室容积增大而增大，轮胎动载荷在附加气室容积较大时有些降低，这是由于空气弹簧动刚度在附加气室容积变大时存在回升，但动刚度总体趋势仍为下降；簧上质量加速度、悬架动行程以及簧下质量加速度变化趋势一致，即随附加气室容积增大而减小，其中，簧上质量加速度、悬架动行程在附加气室容积为0～3 L时变化较其他区域明显，这是由于在该区域内空气弹簧动刚度变化较快.由此可知，适当增加附加气室容积可有效降低簧上质量加速度、动行程，但同时轮胎动载荷、电动机偏心距及不平衡电磁力会增大.

3.2 HDD-AS系统幅频特性分析

电动机偏心距、簧上质量加速度、悬架动行程、轮胎动载荷以及簧下质量加速度在不同附加气室容积时对路面不平度的传递特性如图10所示，其中G(·)为增益.

图10 不同附加气室HDD-AS系统响应幅频特性

从图10可以看出：由于电动机不平衡电磁力的影响，HDD-AS系统幅频特性在60～70 Hz区域内出现了共振峰，表明电动机不平衡电磁力对空气悬架系统响应在60～70 Hz频段产生了较大的影响；电动机不平衡电磁力对轮胎动载荷影响最大，降序依次为簧下质量加速度、簧上质量加速度，最后为悬架动行程；随着附加气室容积的增加，空气弹簧刚度下降，由于低频时空气弹簧与附加气室气体交换充分，高频时气体时滞特性凸显，所以高频段幅频特性对带附加气室空气弹簧刚度变化敏感性不高，低频段幅频特性却较为敏感；电动机偏心距、簧上质量加速度、轮胎动载荷幅频特性低频共振峰(1～2 Hz)振幅随空气弹簧刚度下降而减小，共振频率向高频方向移动；频率大于2 Hz时，其幅值变化趋势相反，且在频率逐渐变高时幅值趋于一致；悬架动行程幅频特性幅值在0.8 Hz前随空气弹簧动刚度减小而增大；低频共振峰(1～2 Hz)振幅随空气弹簧刚度下降而减小，共振频率向高频方向移动.由于簧下质量共振峰共振频率较高，空气弹簧刚度变化对其幅频特性影响不大.所以，适当增加附加气室容积可有效抑制电动机低频区域因路面激励引起的振动，并可提升空气悬架在低频激励输入时部分性能的表现，但会使轮胎动载荷在低中频共振峰间区域幅值增大.

电动机偏心距、簧上质量加速度、悬架动行程、轮胎动载荷以及簧下质量加速度在不同阻尼系数时对路面不平度的传递特性如图11所示.

从图11a可以看出：随着阻尼系数的增大，电动机偏心距幅频特性低频共振峰(1～2 Hz)幅值减小，共振频率向高频区域移动；中频共振峰(6～8 Hz)幅值减小，共振频率向低频区移动；高频共振峰(60～70 Hz)幅值减小，共振频率不变；低中频间频率区域、中高频间频率区域幅值变化趋势与共振峰幅值变化趋势相反，随阻尼系数增大而增大.

从图11b可以看出：随着阻尼系数的增大，簧上质量加速度幅频特性低频共振峰(1～2 Hz)幅值减小，共振频率向高频区域移动；中频共振峰(6～8 Hz)幅值基本不变，共振频率向低频区移动；高频共振峰(60～70 Hz)幅值增大，共振频率不变，这表明阻尼系数的增大会使电动机不平衡电磁力对簧上质量加速度的影响增大；低中频间频率区域、中高频间频率区域幅值随阻尼系数增大而增大.

从图11c可以看出：随着阻尼系数的增大，悬架动行程在全频率段的幅频特性幅值减小，低频共振频率向高频方向移动，高频共振频率向低频方向移动.

从图11d可以看出：随着阻尼系数的增大，轮胎动载荷幅频特性低频共振峰(1～2 Hz)幅值减小，共振频率向高频区域移动；中频共振峰(7～8 Hz)幅值减小，共振频率基本不变；高频共振峰(60～70 Hz)幅值减小，共振频率不变；低中频间频率区域幅值随阻尼系数增大而增大，中高频间频率区域随阻尼系数增大而减小，并随频率增大逐渐趋于一致.

从图11e可以看出：随着阻尼系数的增大，簧下质量加速度在全频率段的幅频特性幅值减小，第1个共振峰共振频率(7～8 Hz)基本不变.