海水海砂再生混凝土单轴受压应力-应变全曲线

张凯建，肖建庄，3，张青天

（1.同济大学土木工程学院，上海200092；2.福州大学土木工程学院，福建福州350116；3.同济大学土木工程防灾国家重点实验室，上海200092）

由于河砂资源短缺，价格不断上涨，因此我国自20世纪90年代以来在沿海地区开始使用海砂［1］。值得注意的是，上述应用的海砂基本是淡化海砂，以避免高氯离子（Cl-）含量对钢筋的锈蚀。据调查，我国近海5～50 m范围内，有丰富的粒径大于细砂的海砂资源储备（达到了380亿m3），可用作中细砂［2］。考虑到纤维增强复合材料（FRP）有较高的强重比以及抗腐蚀性能，Teng等［3］在2011年首次提出FRP-海水海砂混凝土的组合形式，这为原状海水海砂混凝土的使用创造了条件。另一方面，我国建筑废物排放量逐年增加，2019年超过18.5亿吨（不含渣土）［4］，实现废混凝土的再生利用是有效处理建筑固废的科学方式。将废混凝土破碎加工成再生粗骨料，部分（质量分数15%以上）或全部代替天然骨料配制而成的新混凝土，称为再生混凝土［5］。

将海水海砂与再生骨料组合后制备的混凝土，称为海水海砂再生混凝土（SSRAC，本研究中再生骨料为再生粗骨料）。海水海砂再生混凝土既可以充分利用丰富的海水海砂资源，也可以消纳废弃混凝土，同时减少矿山的开采，具有显著的生态性。海水海砂再生混凝土的力学性能已经引起重视［6］。目前，关于海水海砂再生混凝土应力-应变关系的研究还较少。Guo等［7］探究了海水海砂普通混凝土的应力-应变曲线，发现弹性模量和峰值应变降低。本研究中将基于试验探究海水海砂再生混凝土单轴受压的破坏模式，讨论不同应变率下海水海砂再生混凝土的单轴受压应力-应变曲线。

1 试验过程

1.1 材料物理性能指标

试验所用的再生粗骨料（RCA）粒径为5～25 mm，细骨料为河砂、海砂以及贝壳砂。粗骨料物理指标测试结果如表1所示。由表1可知，再生粗骨料的堆积密度和表观密度都低于天然粗骨料（NCA），再生粗骨料的泥块含量、压碎指标和吸水率都明显好于天然粗骨料。细骨料物理指标测试结果如表2所示。由表2可知，海砂中Cl-含量为0.057%，高于贝壳砂，海砂和贝壳砂中的贝壳含量分别为2.31%和99.43%。试验所用海水依据美国材料实验协会（D1141―98）［8］关于海水制备规程中所给的化学成分配制得到。

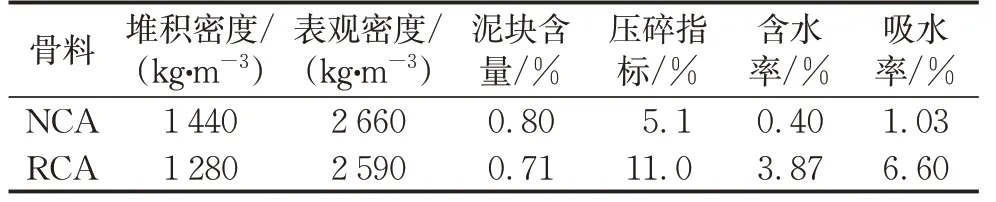
表1 粗骨料物理性能Tab.1 Physical properties of coarse aggregates

表2 海砂、贝壳砂物理性能Tab.2 Physical properties of sea sand and shell sand

河砂、海砂以及贝壳砂的级配曲线如图1所示。级配曲线显示，不同类别砂的级配曲线大部分在国家标准［9］规定的上下限内，海砂中小于0.6 mm孔径的累积筛余率和贝壳砂中小于1.0 mm孔径的累积筛余率略高于上限值。此外，与国家标准［9］相比，ISO标准［10］中的上下限更为严格。

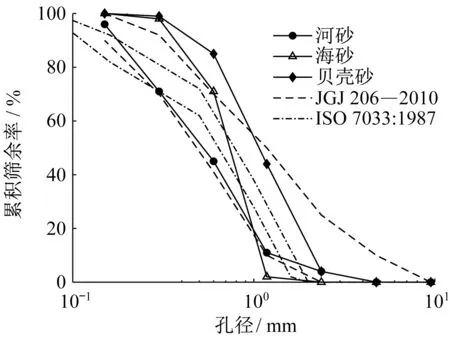
图1 砂骨料级配曲线Fig.1 Grading curves of sand aggregates

1.2 配合比设计及试块浇筑

混凝土的水灰比为0.47，依据贝壳含量及再生粗骨料取代率将试块分为9组，其中贝壳含量分为纯海砂、海砂与贝壳砂含量为4∶1的混合砂2组。再生粗骨料取代率为0、50%和100%。棱柱体试件尺寸为100 mm×100 mm×300 mm，每组制作6个试件。海水海砂再生混凝土配合比如表3所示。试件编号中RAC表示再生混凝土，其后数字表示再生粗骨料取代率，%；M表示贝壳含量为2.33%，H表示贝壳含量为21.73%；SSNAC表示海水海砂混凝土。水泥等级为42.5。根据表1中再生粗骨料含水率和吸水率确定每组的附加水用量（吸水率和含水率之差与再生粗骨料质量的乘积）［11］，附加水与该组的自由水类别相同。减水剂为聚羧酸高效减水剂，用量为3.19 kg·m-3。混凝土试件采用室外养护的方式，直至达到预定龄期。

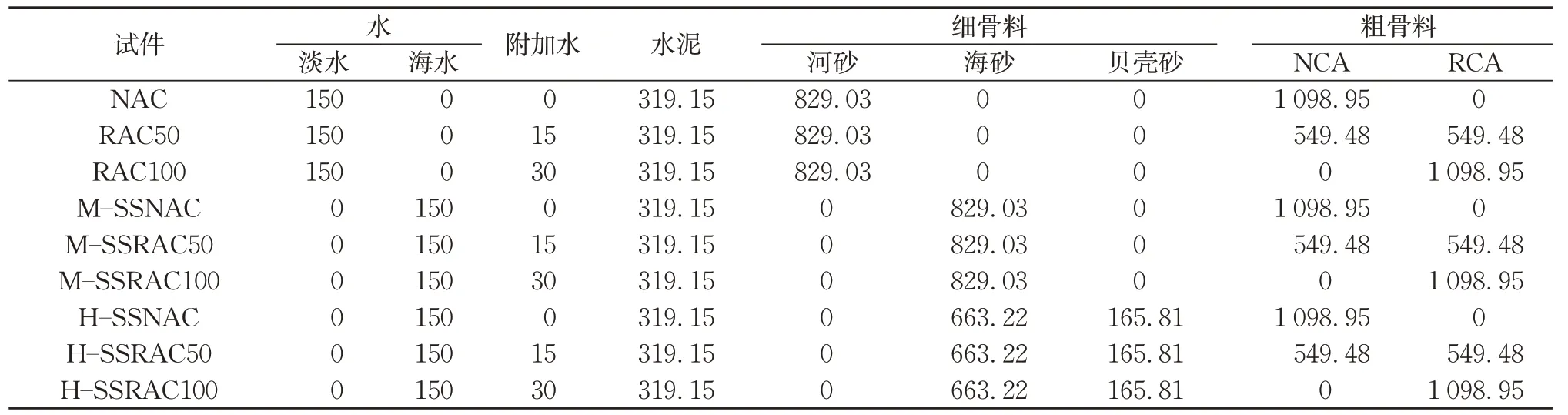
表3 海水海砂再生混凝土配合比Tab.3 Mix proportions of SSRAC 单位：kg·m-3

1.3 试件加载

所有试件在浇筑120 d后进行试验。加载装置为MTS 815.02电液伺服试验系统［11］。采用位移加载，加载速率分别为0.003 mm·s-1和3.000 mm·s-1，对应的应变率分别为10-5s-1和10-2s-1。加载程序分为预加载和正式加载。在预加载过程中采用力控制，预加载峰值荷载设置为5 kN；正式加载采用位移控制，加载速率根据不同的应变率要求进行设置，最大位移设置为3.0 mm。

2 试验结果分析

2.1 单轴受压破坏模式

图2给出了10-5s-1和10-2s-1应变率下试件的破坏模式。在加载初期，棱柱体试件没有裂缝产生。随着荷载的增大，试件端部开始出现细小的竖向裂缝，而且裂缝数量逐渐增多。达到峰值应力后，荷载缓慢降低，开始出现比较明显的竖向裂缝，之后裂缝贯通，形成试件破环时的主裂缝。结果表明，再生粗骨料取代率、海水海砂含量以及贝壳含量对试件破坏模式的影响不显著，试件破坏时最终形成一条连接试件上部和下部的贯通主裂缝。

2.2 应力-应变全曲线特征指标

对所测得的相同试件在相同应变率下的3条试验曲线进行统计分析，得到曲线的均值，如图3～5所示。图3～5中，NAC-2、NAC-5、RAC50-2、RAC50-5、RAC100-2、RAC100-5分别表示应变率为10-2s-1和10-5s-1下试件。

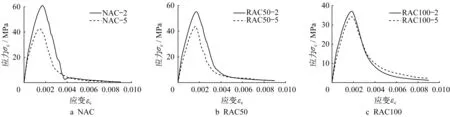
图3 NAC、RAC应力-应变均值曲线Fig.3 Mean stress-strain curves of NAC and RAC

应力-应变曲线的特征指标包括峰值应力、峰值应变和弹性模量（0.5%～30.0%峰值应力对应的割线模量），试验结果如图6～8所示。

由图6可知，10-2s-1应变率下应力-应变曲线的特征指标高于10-5s-1应变率下的特征指标。在10-2s-1应变率下，RAC50峰值应力提高了26.80%，峰值应变提高了7.41%，弹性模量提高了19.80%；RAC100的峰值应力提高了7.54%，峰值应变相当，弹性模量提高了28.20%。此外，随着再生粗骨料取代率的增加，不同应变率下再生混凝土的峰值应力整体呈下降趋势（见图6a），峰值应变逐渐增加（见图6b），弹性模量显著降低（见图6c）。

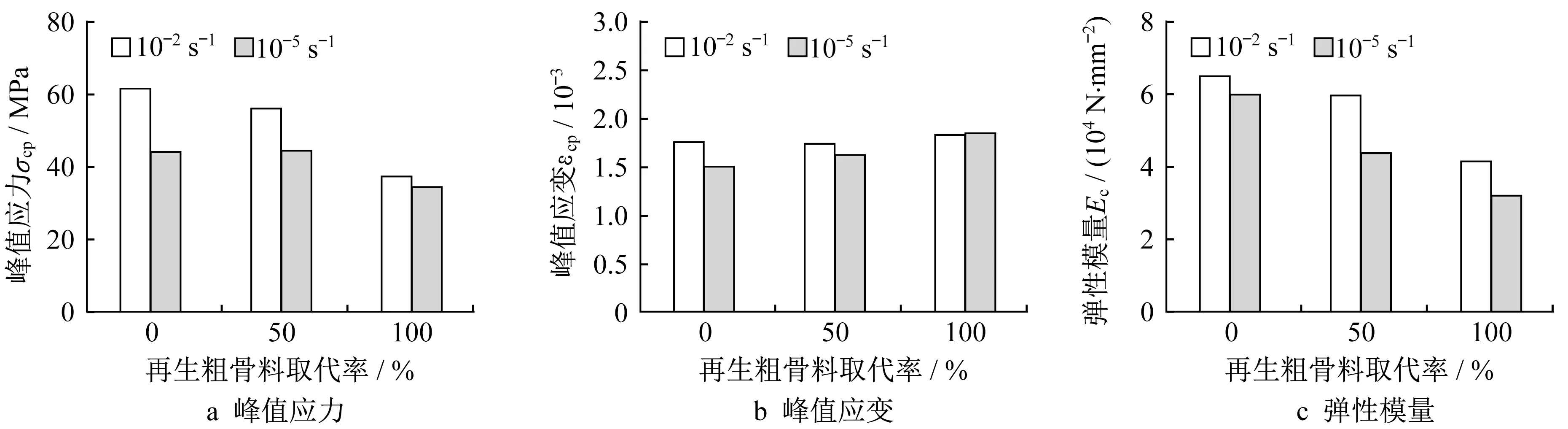
图6 NAC、RAC应力-应变曲线特征指标Fig.6 Characteristic indices of stress-strain curves of NAC and RAC

由图7可知，10-2s-1应变率下M-SSRAC的特征指标整体上高于10-5s-1应变率下的特征指标。10-2s-1应变率下，M-SSRAC100的峰值应力提高了21.70%，M-SSNAC和M-SSRAC100的峰值应变随应变率增大而增加，10-2s-1应变率下MSSRAC50的弹性模量提高了7.75%，M-SSRAC的峰值应力随再生粗骨料取代率的增加而增大。与M-SSNAC相比，10-5s-1应变率下M-SSRAC50的峰值应力提高了24.10%，10-2s-1应变率下提高了23.10%。M-SSRAC50和M-SSRAC100的弹性模量随再生粗骨料取代率增加呈下降趋势，与MSSNAC相比，2种应变率下M-SSRAC50的弹性模量分别降低了11.30%和19.20%，M-SSRAC100的弹性模量分别降低了17.70%和29.60%。

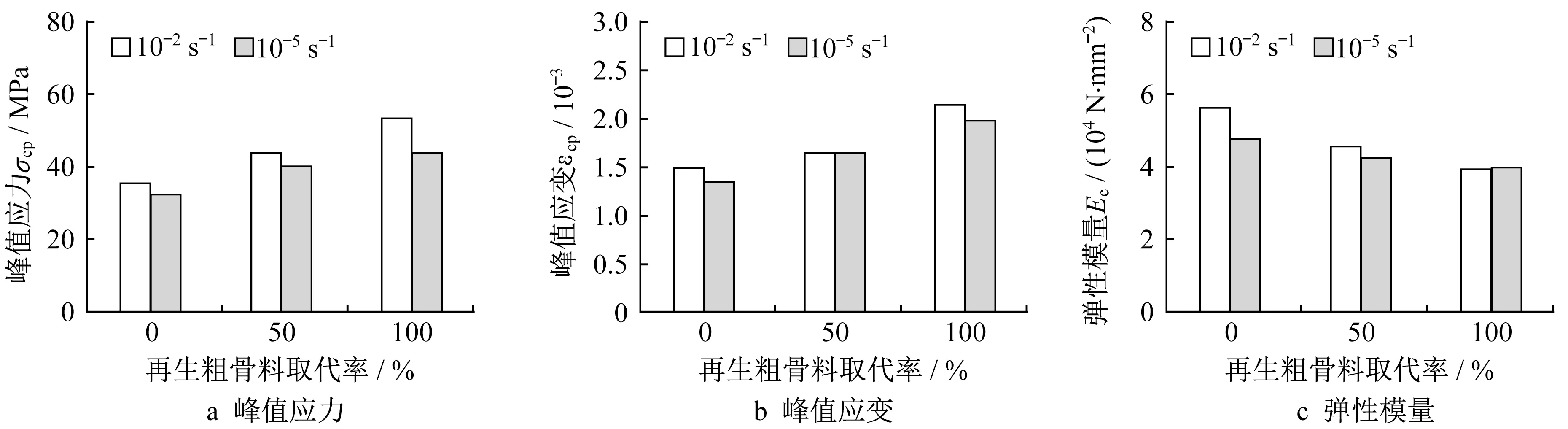
图7 M-SSNAC、M-SSRAC应力-应变曲线特征指标Fig.7 Characteristic indices of stress-strain curves of M-SSNAC and M-SSRAC

由图8可知，H-SSRAC的峰值应力和弹性模量随应变率增大而增大，而峰值应变呈下降趋势。与10-5s-1应变率相比，10-2s-1应变率下H-SSRAC50和H-SSRAC100的峰值应力分别提高了3.04%和6.38%。对于峰值应变，10-2s-1应变率下的值显著低于10-5s-1应变率下的值。与10-5s-1应变率相比，10-2s-1应变率下弹性模量显著提升，H-SSRAC50和H-SSRAC100的弹性模量分别提升了41.80%和40.40%。峰值应力随再生粗骨料取代率的发展趋势不明显。峰值应变随再生粗骨料取代率增加而逐渐增大，在10-5s-1应变率下，峰值应变随再生粗骨料取代率基本呈线性增长。随着再生粗骨料取代率的增加，弹性模量逐渐降低，与H-SSNAC相比，10-5s-1应变率下H-SSRAC50的弹性模量降低了19.70%，10-2s-1应变率下降低了17.40%，2种应变率下H-SSRAC100的弹性模量分别降低了24.70%和23.40%。

图4 M-SSNAC、M-SSRAC应力-应变均值曲线Fig.4 Mean stress-strain curves of M-SSNAC and M-SSRAC

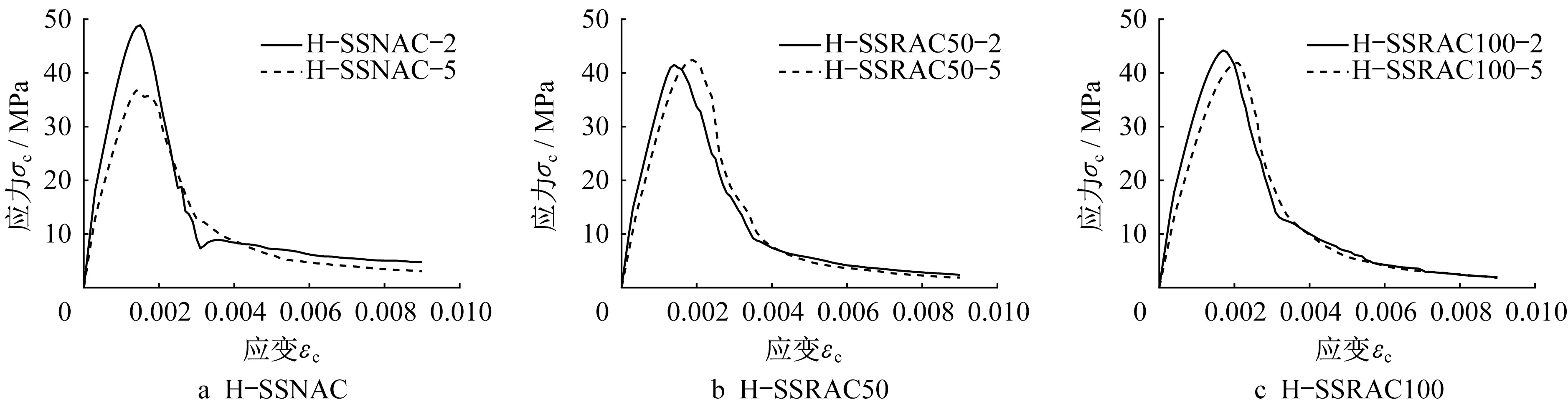
图5 H-SSNAC、H-SSRAC应力-应变均值曲线Fig.5 Mean stress-strain curves of H-SSNAC and H-SSRAC

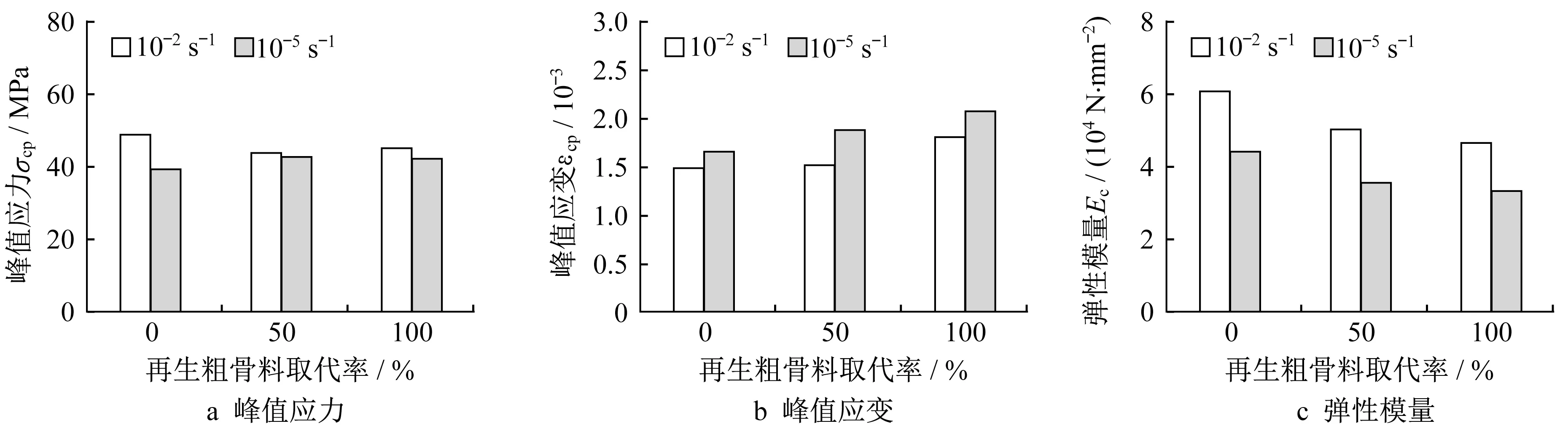
图8 H-SSNAC、H-SSRAC应力-应变曲线特征指标Fig.8 Characteristic indices of stress-strain curves of H-SSNAC and H-SSRAC

2.3 动态增长因子

特征指标的动态增长因子定义为动态应变率下的特征指标与准静态下的特征指标的比值。图9给出了特征指标的动态增长因子（10-2s-1与10-5s-1应变率下特征指标的比值）。由图9a可知，对于RAC，随着再生粗骨料取代率的增加，峰值应力的动态增长因子Dσ逐渐降低，NAC、RAC50和RAC100的Dσ依次为1.41、1.27和1.08；对于M-SSRAC，当再生粗骨料取代率由0增加50%时，Dσ变化不明显（1.10变化到1.09），在再生粗骨料取代率为100%时增加到1.22；H-SSRAC的Dσ变化趋势与M-SSRAC不同，呈先降低后增加的趋势。此外，当再生粗骨料取代率为50%时，随着混凝土中贝壳含量的增加，Dσ逐渐降低，而在其他再生粗骨料取代率时无明显发展趋势。

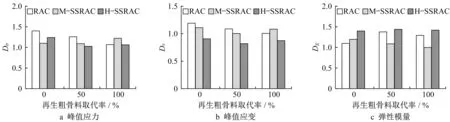
图9 特征指标的动态增长因子Fig.9 DIF of characteristic indices

对于峰值应变，由图9b可知，RAC的峰值应变动态增长因子Dε随再生粗骨料取代率增加逐渐降低，M-SSRAC和H-SSRAC的Dε变化一致，呈先降低后增加趋势，M-SSRAC的Dε高于H-SSRAC的Dε。当再生粗骨料取代率为0和50%时，随着混凝土中贝壳含量的增加，Dε逐渐降低；当再生粗骨料取代率为100%时，Dε随贝壳含量的增加先增加后降低。

由图9c可知，RAC弹性模量动态增长因子DE随再生粗骨料取代率先增加后降低，M-SSRAC的DE随再生粗骨料取代率增加呈下降趋势，依次为1.18、1.08和0.99，而H-SSRAC的DE随再生粗骨料取代率增加基本不变，为1.40左右。随着贝壳含量的增加，当再生粗骨料取代率为0时，DE逐渐增加，而当再生粗骨料取代率为50%和100%时，DE都呈先降低后增加的趋势，H-SSRAC的DE为所有组中的最大值。

3 海水海砂再生混凝土CT测试

利用电子计算机断层扫描（CT）技术（机器型号为NIKON XTH 320/225，旋转速度为120 rpm，电压和电流分别为300 kV和250 mA，切片厚度为1.0 mm），测试了海水海砂再生混凝土内部的孔隙分布。海水海砂再生混凝土样品为边长78 mm的立方体，将扫描的二维图像进行渲染生成体积图像，对海水海砂再生混凝土内部的不同相和孔结构进行了三维重建。图10给出了不同孔径孔隙的空间分布。

图10 海水海砂再生混凝土孔结构Fig.10 Pore structures of SSRAC specimens

对于RAC，随着再生粗骨料取代率的增加，孔隙率显著增加，NAC的孔隙率为1.850%，RAC100的孔隙率增加到1.989%，这主要是由于再生粗骨料的加入引入了更多的疏松多孔的界面过渡区［12］，导致孔隙率增加。海水海砂加入后，孔隙率降低。M-SSNAC的孔隙率为2.900%，M-SSRAC100的孔隙率降低到1.960%，降低了32.4%；H-SSNAC的孔隙率为2.220%，H-SSRAC100的孔隙率降低到1.945%，降低了12.4%。海水海砂再生混凝土孔隙率的测试结果为应力-应变曲线中峰值应力的测试结果提供了解释，即孔隙率越高，峰值应力越低。考虑到再生粗骨料表面通常附着未水化的水泥，海水海砂加入后，未水化水泥与Cl-发生反应并形成填充再生粗骨料表面孔隙的产物（Friedel盐［13］）。因此，适量的Cl-可弥补再生粗骨料的缺陷，降低孔隙率。另一方面，海水海砂中含有SO-23，导致水化产物中钙矾石的含量增加［14］，体积膨胀更为严重。由于SSRAC的弹性模量比SSNAC低，这为钙矾石的体积膨胀提供了缓冲作用，减少了内部膨胀孔隙的产生，因此再生粗骨料的加入降低了孔隙率。

加入海水海砂后，贝壳含量的增加可以降低再生混凝土的孔隙率。RAC100、M-SSRAC100和HSSRAC100的贝壳含量依次增加，孔隙率逐渐降低。实际上，现有文献［1］的研究显示，贝壳含量对混凝土力学性能的影响趋势不明显，还需要更多相关的研究进行深入分析。

4 应力-应变全曲线预测

4.1 预测结果对比

利用现有的3种模型来预测再生混凝土本构曲线，分别来自欧洲规范［15］、肖建庄等［16］研究和中国规范［17］。利用上述模型计算10-5s-1应变率下海水海砂再生混凝土的应力-应变全曲线，与相同应变率下试验曲线进行对比，如图11～12所示。

由模型预测曲线与试验曲线的对比可知，对于应力-应变曲线的上升段，3种模型的预测曲线与试验结果比较吻合。对于下降段，不同模型的预测效果不同。对于M-SSRAC，由图11可知，中国规范模型［17］与试验曲线更为吻合。对于H-SSRAC，当再生粗骨料取代率为零时（H-SSNAC），图12a显示中国规范模型［17］与试验曲线更为吻合；肖建庄等模型［16］的预测曲线与H-SSRAC50和H-SSRAC100的试验曲线更为吻合，如图12 b和c所示。

4.2 动态应力-应变全曲线

基于试验数据，同时参考现有文献［18］，暂不考虑峰值应变的变化［18］，在式（1）和（2）确定动态峰值应力σd，cp和动态弹性模量Ed，c后，代入准静态应力-应变模型用来描述海水海砂再生混凝土的动态应力-应变全曲线。

选取中国规范模型［17］描述海水海砂再生混凝土的动态本构关系，确定动态应变率下的峰值应力和弹性模量后，通过试验数据拟合得到下降段系数。下降段修正系数如表4所示。将修正后的下降段系数代入中国规范模型［17］，预测曲线和试验测试曲线对比如图13～14所示。

图13 M-SSNAC、M-SSRAC修正模型预测曲线与试验结果对比Fig.13 Comparison between predicted curves from modified model and tested results for M-SSNAC and MSSRAC

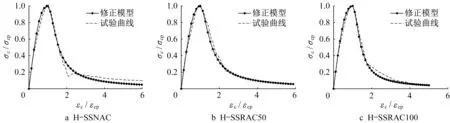
图14 H-SSNAC、H-SSRAC模型预测曲线与试验曲线对比Fig.14 Comparison between predicted curves from modified model and tested results for H-SSNAC and HSSRAC

表4 下降段修正系数（应变率=10-2 s-1）Tab.4 Modified factor of descending branch（stain rate=10-2 s-1）

在准静态应力-应变模型的基础上，考虑特征指标的动态增长因子后，通过修正模型下降段形状系数，可以很好地描述海水海砂再生混凝土在10-2s-1应变率下的应力-应变全曲线。

5 结论

（1）海水海砂再生混凝土的峰值应力和弹性模量整体上随着应变率的增大而提高。再生粗骨料取代率对不同组的海水海砂再生混凝土峰值应力和峰值应变影响不同，但弹性模量随着再生粗骨料取代率提高显著降低。

（2）随着再生粗骨料取代率的增加，M-SSRAC和H-SSRAC的Dσ呈先降低后增加的趋势；MSSRAC和H-SSRAC的Dε变化一致，呈先降低后增加趋势；M-SSRAC的DE随再生粗骨料取代率增加呈下降趋势，而H-SSRAC的DE随再生粗骨料取代率增加基本不变。

（3）随着再生粗骨料取代率的增加，RAC孔隙率显著增加，而海水海砂的加入会降低孔隙率，贝壳含量的增加也可以降低再生混凝土的孔隙率。

（4）现有3种本构模型的预测曲线与应力-应变曲线的上升段试验结果比较吻合。考虑峰值应力和弹性模量的动态增长因子后，在准静态应力-应变模型的基础上，通过修正模型下降段形状系数，得到了海水海砂再生混凝土的动态应力-应变预测曲线。