下击暴流作用下大跨度平屋盖结构的风荷载分布特性

2022-01-16谢壮宁林韬略成文滔

同济大学学报（自然科学版） 2021年12期

谢壮宁，林韬略，成文滔，2

（1.华南理工大学亚热带建筑科学国家重点实验室，广东广州510640；2.广东保利城市发展有限公司，广东广州510180）

下击暴流是强对流云团中强烈下沉的冷气流撞击近地面暖湿空气后骤然形成的一种极端风，具有很强的随机特性，其研究起源于20世纪70年代［1］。由于毁坏性极强，因此在世界各地导致了多起人员伤亡和建筑结构破坏事故［2］。下击暴流的最大水平风速发生在近地表面，对低矮建筑具有较强的破坏性，因此进行下击暴流作用下的大跨度平屋盖结构的风荷载分布特性研究具有重要的实际意义。

风场特性中的平均风速、湍流强度、脉动风速功率谱、脉动风湍流积分尺度等都会直接影响建筑结构的风荷载分布特性，而下击暴流与普通常态地貌风的风场特性相比有较大差异。Hjelmfelt［3］在分析Joint Airport Weather项目实测数据时发现了下击暴流平均风速随高度升高先增大后降低的分布规律，得到了下击暴流的经典风速剖面图，与传统大气边界层平均风速随高度的升高而增大这一特性有显著差别。Oseguera等［4］、Vicroy［5］、Wood等［6］基于已有的风剖面经验模型，先后建立了下击暴流平均风速沿高度变化的数学解析模型，三者沿高度方向具有相似的分布规律。受限于测试手段和测试难度，长期以来一直罕有见到有关描述下击暴流湍流特征的相关研究结果，Zhang等［7］首次介绍了2019年在北京气象塔的下击暴流实测中得到的325 m高度以下的湍流度和风速功率谱分布，是迄今为止能够检索到的为数不多的在该领域针对下击暴流湍流特征的研究。湍流经验模型的缺少在客观上导致下击暴流模拟的盲目性，进而影响相关建筑风洞试验结果的可靠性。

除了下击暴流的湍流特征缺失之外，下击暴流本身的模拟就具有较大的难度。近年来，国内外学者陆续建造了多座不同类型的下击暴流物理试验模拟发生装置。Holmes［8］较早地借助冲击射流装置开始了下击暴流的物理模拟，随后Wood等［6］、Letchford等［9］、Chay等［10］基于壁面射流模型研制出了喷射出口朝向不同的下击暴流模拟装置，并对风场特性展开了研究。陈勇等［11］建造了国内首座下击暴流专用模拟平台，研究了射流参数对冲击风流场的影响。已有物理试验模拟方法主要是冲击射流模拟，因而都不同程度地存在所能模拟的风场尺度太小的情况，难以满足较大缩尺比下开展大跨度屋盖结构试验的需要。段旻等［12］在常规3 m宽度大气边界层风洞试验段内模拟出平均风速剖面与经典模型相吻合的下击暴流风场，并开展了针对圆柱形大跨度屋面的相关试验研究，但还缺乏对湍流强度和脉动风速功率谱等重要指标的分析。

在文献［12］的基础上进一步在5 m宽度的边界层风洞中对下击暴流风场进行模拟，并与已有平均风速经验模型和文献［7］的实测下击暴流湍流特征进行比较。以一个大跨度平屋盖结构为研究对象，对比了下击暴流风场与大气边界层B类风场对该结构屋面风压分布的影响，总结了下击暴流作用下大跨度平屋盖表面风压的分布规律，可为大跨度平屋盖的抗下击暴流设计提供参考。

1 试验设备

1.1 模拟装置

试验开展于华南理工大学风洞实验室，试验段长24.0 m、宽5.4 m、高3.0 m，转盘可在0～360°风向角内转动，半径为2 m，试验段风速在0～30 m·s-1内连续可调。

所采用的下击暴流模拟装置［13］整体尺寸为4 800 mm×2 800 mm×1 500 mm，主要由竖向支架、横向支架、斜导流板、滑块、导轨、螺栓和滚轮等部分组成，结构示意图和实物照片如图1所示。斜导流板通过滑块与竖向支架相连，由螺栓进行固定，作用为风场中下部风速加速。斜导流板上下沿的可调高度范围均为100 mm至2 700 mm，通过高度参数的调整可实现不同比例风场的模拟。底部滚轮可带动装置水平移动以改变试验模型和下击暴流风场的相对距离。

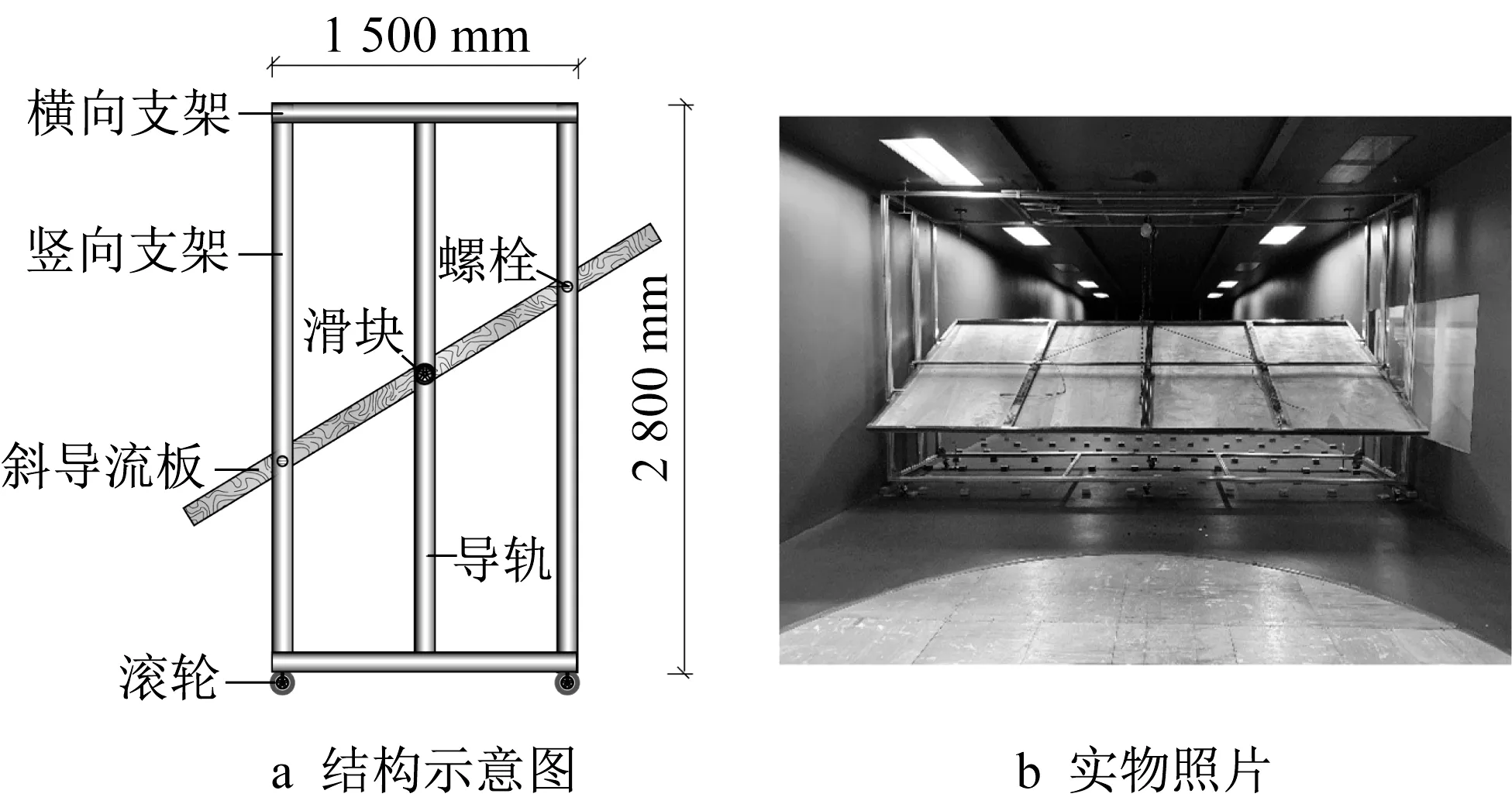
图1 下击暴流模拟发生装置Fig.1 Experimental apparatus for downburst simulation

风场调试选取1∶300的比例尺，斜导流板下沿高度设置为0.9 m，上沿高度设置为1.5 m。下击暴流风场模拟的观测点布置如图2所示，径向共有5个观测点，与斜导流板下沿中心o点的径向距离x分别为2.85、3.10、3.35、3.60、3.85 m。基于下击暴流风场的空间分布特性，设定实际观测高度为0～225 m，结合比例尺得到相应的实验室观测高度z为0～0.75 m。沿高度方向上按0.10 m设置观测点，由于风场底部的变化情况极为激烈，因此对底层观测点进行了加密。

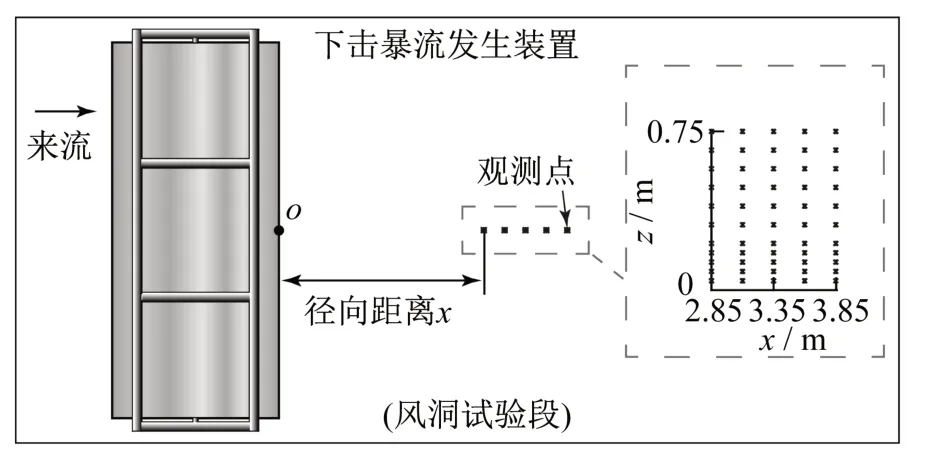
图2 观测点布置Fig.2 Layout of observation points

为比较下击暴流与大气边界层常态风场的差异，选取B类地貌作为对照工况。采用澳大利亚TFI Cobra三维脉动风速测量系统和计算机自动控制的三维移动测量系统来获取观测点处的风速时程，可同时测量三维风速和静态压力。试验的样本总长度为40 960，采样频率为400 Hz，采样时长为102.4 s。

1.2 试验模型

大跨度平屋盖刚性测压模型的比例尺为1∶300，整体尺寸为1 000 mm×667 mm×133 mm。屋面测点共有467个，采用中心对称的方式布置，并在风荷载变化剧烈的部位，如屋面边缘和角区进行了加密处理，试验模型和测点布置如图3所示。采用美国PSI公司Initium测压系统进行试验风压数据采集，采样时长为62.3 s，采样频率为328.8 Hz，样本长度为20 480。为保证对比的客观性，选取模型屋面高度处的风压作为无因次化的参考风压。风压系数的表达式如下所示：

图3 试验模型和测点布置Fig.3 Test model and layout of measuring points

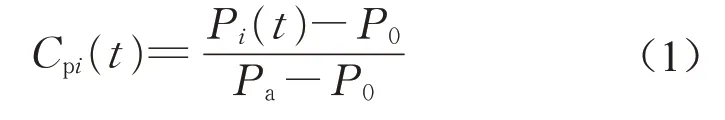
式中：Cpi(t)为测点i处的风压系数序列；Pi(t)为测点i处的风压序列；Pa为参考高度处的总压；P0为参考高度处的静压。根据风压系数时程统计得到平均风压系数，并借助Feng等［14］提出的基于样本独立性的短时程样本极值风压估计方法统计得到相应的极小、极大风压系数。

2 流场模拟结果

通过调整斜导流板上下沿高度，在风洞中较好地实现了1∶300比例尺下击暴流风场的模拟。虽然下击暴流风场在不同径向位置的分布有所差异，但是存在某个位置的平均风速剖面与经典模型最为相近，将该位置定义为“最佳剖面”位置。

2.1 水平风速剖面

图4为下击暴流水平风速剖面的模拟结果，并与下击暴流经典模型以及GB 50009―2012《建筑结构荷载规范》［15］B类地貌风场的试验结果进行比较。为便于分析，使用下击暴流风场水平风速最大值umax对水平风速u进行无因次化（u/umax），即令理论最大水平风速为1。由图4可见，不同径向位置的水平风速规律一致，均为随高度升高先增加后降低，在高度zmax=75 m处达到最大值，均形成了下击暴流的特色剖面，并且明显有别于B类风场随高度增加而指数型增长的变化情况。径向距离x=3.35 m处的水平风速剖面整体处于Vicroy［5］、Wood等［6］的水平风速剖面之间，可认为该剖面为“最佳剖面”。

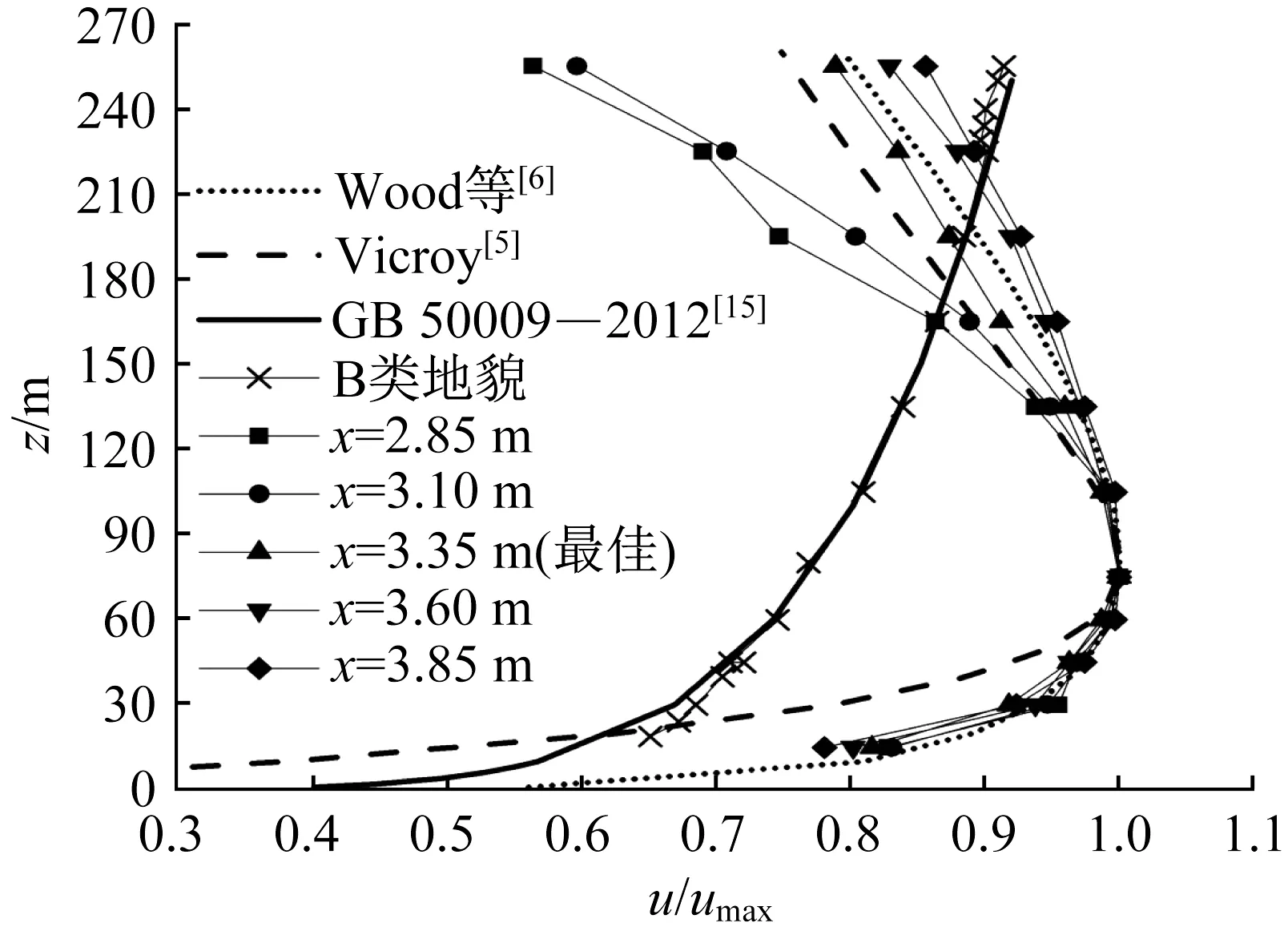
图4 水平风速对比Fig.4 Comparison of horizontal wind velocity

2.2 竖向风速剖面

图5为下击暴流“最佳剖面”位置的竖向风速剖面的试验结果。由于下击暴流是俯冲气流带来的气候现象，因此对于竖向剖面的研究是下击暴流风场研究中非常重要的构成部分。同理，使用下击暴流风场竖向风速最大值vmax对竖向风速v进行无因次化（v/vmax）。由图5可见，在“最佳剖面”位置处，当高度小于30 m时，竖向风速随高度的提升而不断增强，这是由于来流风经过下击暴流发生器斜导流板的倾角后产生了竖直向下的分量；当高度从30 m逐渐增大时，由于下击暴流发生器所产生的竖直向下分量不断衰减，风场中的竖向风速也随之减小。最佳风速剖面位置处竖向风速最大值的风速矢量与水平方向所成角度大致为5.08°，竖向风速与水平风速的比例为0.08。“最佳剖面”处的竖向风速在高度方向与水平风速有相似的分布规律，但竖向风速最大值发生高度要低于水平风速。

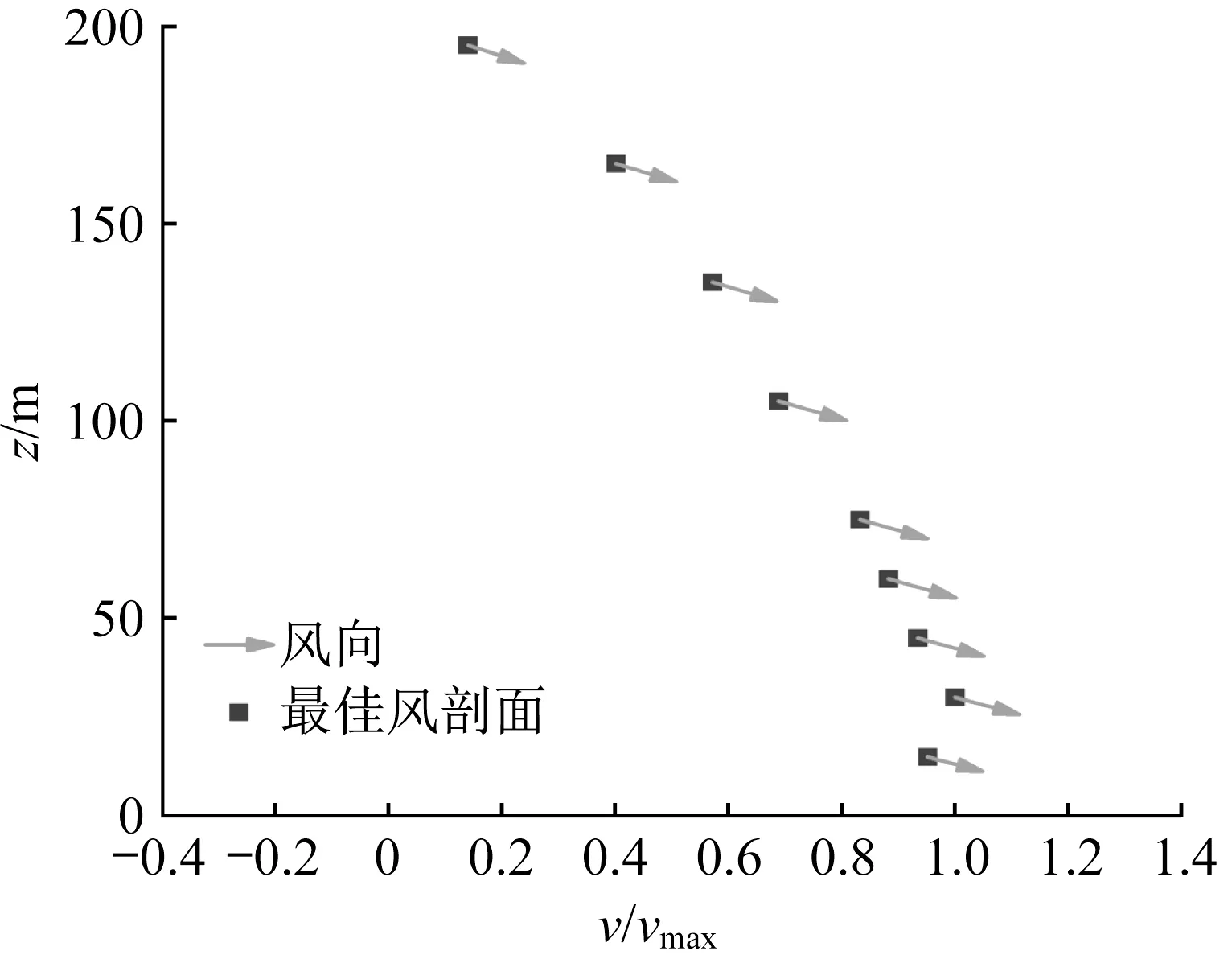
图5 竖向风速对比Fig.5 Comparison of vertical wind velocity

2.3 脉动风速湍流强度剖面

“最佳剖面”位置的顺风向湍流特性分布如图6所示。由图6可见，随着高度的增加，在“最佳剖面”位置处观测点的顺风向湍流强度先衰减后增强，与B类地貌的顺风向湍流强度随高度增加而衰减的变化规律相差较大，并且整体高于B类地貌风场结果。在75 m高度以下试验风场的顺风向湍流强度分布与实测结果较为接近，整体差异小于0.03。由于大跨度平屋盖测压模型的实际高度仅为40 m，因此可以认为试验风场的顺风向湍流强度已满足测压试验的需求。

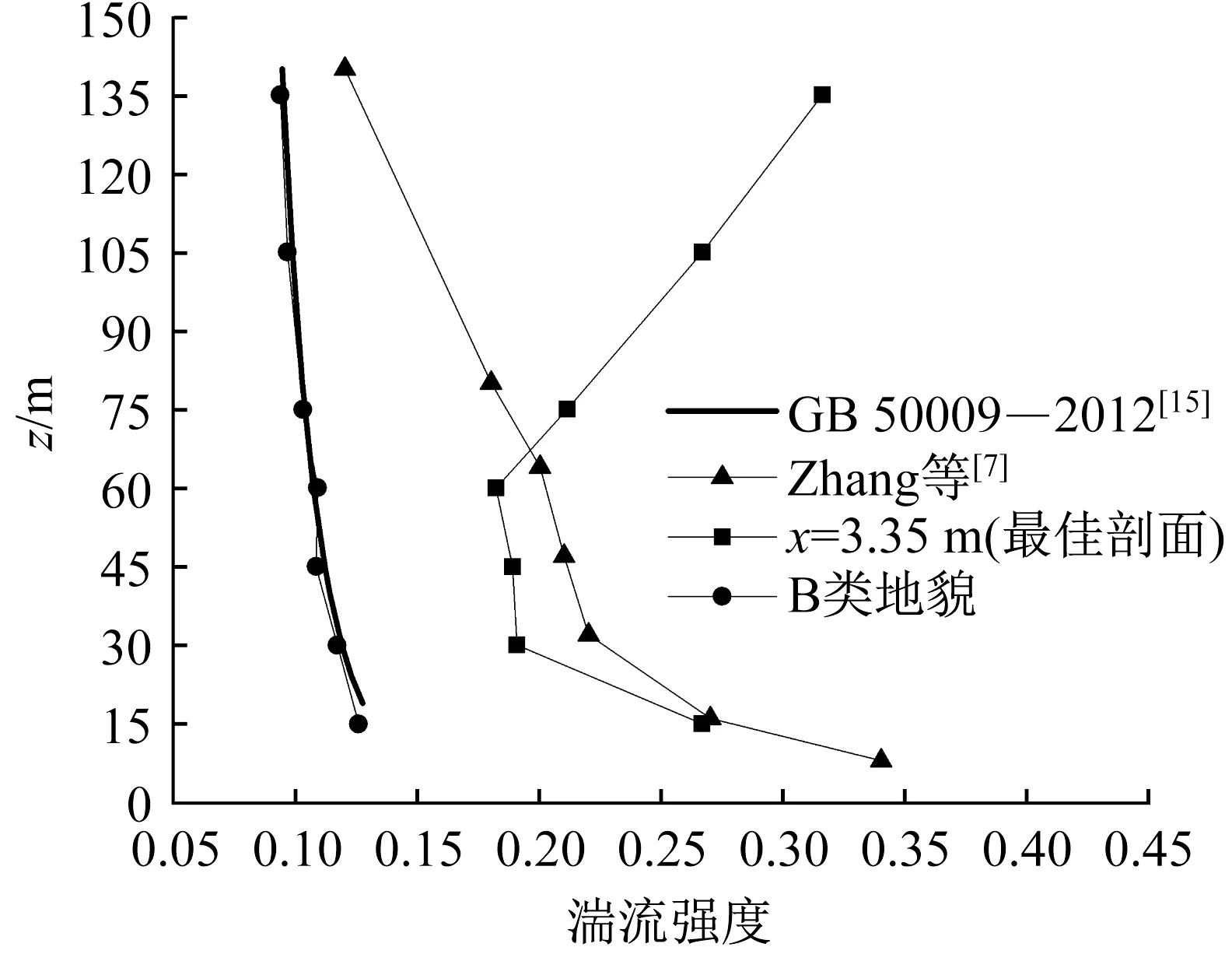
图6 顺风向湍流强度对比Fig.6 Comparison of along-wind turbulence intensity

2.4 脉动风速功率谱

图7为屋面高度和最大水平风速所在高度的无因次顺风向风速功率谱。由图7可见，B类地貌风速功率谱和Von-Karman谱基本吻合，下击暴流水平风速功率谱的峰值能量明显高于B类风场的相应结果，并且谱线形状更为陡峭。试验风速功率谱在卓越频率和谱线形状上与Zhang等［7］实测结果相近，仅在峰值能量上略高于实测相应值。风速功率谱的相似性隐含脉动风湍流积分尺度的相似性。图7中，Su(f)为水平脉动风速功率谱，Sw(f)为竖向脉动风速功率谱，f为脉动风频率，Lxu为湍流积分尺度，Ux为水平平均风速，Uw为竖向平均风速，σ2u为水平脉动风速均方根值，σ2w为竖向脉动风速均方根值，Z为竖向高度。

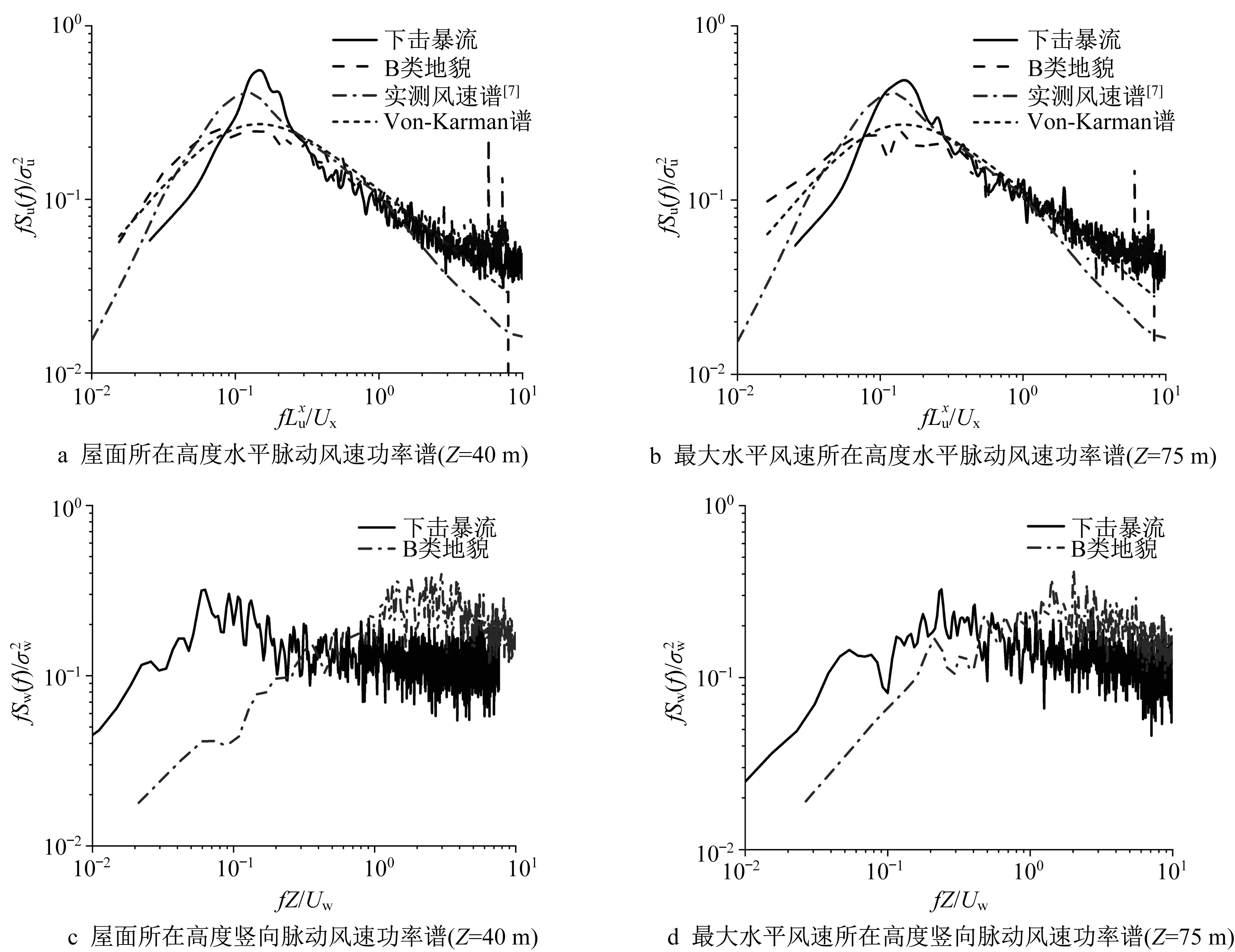
图7 脉动风速功率谱对比Fig.7 Comparison of fluctuating wind power spectrum

总体而言，试验模拟下击暴流风场的平均风速剖面、湍流强度剖面和脉动风速功率谱与已有的经验模型和实测结果对比具有很高的相似性，从而保证了实验室所模拟风场的有效性和可信度。由以上结果可见，所模拟风场在一定的测量范围内满足测压试验的需求。

3 平屋盖风压分布的试验结果

《建筑结构荷载规范》是建筑结构设计的主要依据。规范里关于风荷载的内容是针对大气边界层常态风场而提出的，明显不适用于下击暴流风荷载。因此，在风洞实验室中准确模拟出下击暴流风场，并对大跨度平屋盖结构开展抗风性能研究具有重要意义。在前文较为理想地模拟出下击暴流和B类风场的基础上，进一步考察不同风场作用下大跨度平屋盖结构的风压分布特性。

3.1 最佳风速剖面下的风压分布特征

考虑到篇幅和屋面基本对称性，图8与图9分别为0°和45°风向角下击暴流最佳风速剖面下的风压分布特征。参考风压的取值高度取屋面高度40 m处，图中“■”和“●”分别为风压系数的最小值和最大值。由图8与图9可见，平均风压系数和极小风压系数均为负值，极小风压系数绝对值最大值出现在45°风向角，平均风压系数和极小风压系数绝对值最大值出现在屋面角区，这是由锥形涡引起的。极大风压系数除了在屋面迎风区域为负值以外，其他区域均为正值。

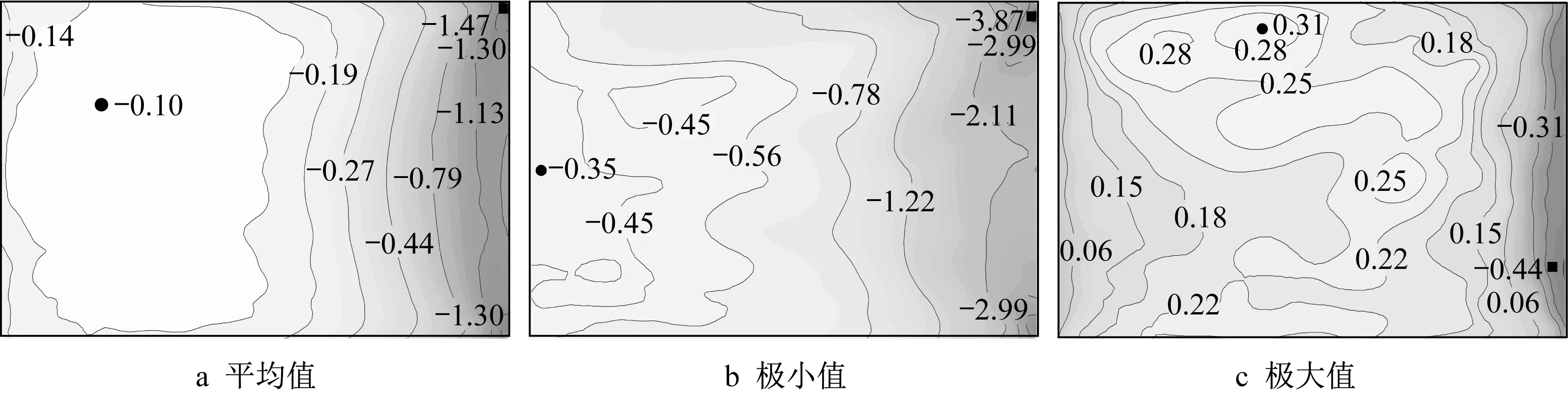
图8 0°风向角风压系数分布Fig.8 Distribution of wind pressure coefficients at 0°wind direction angle

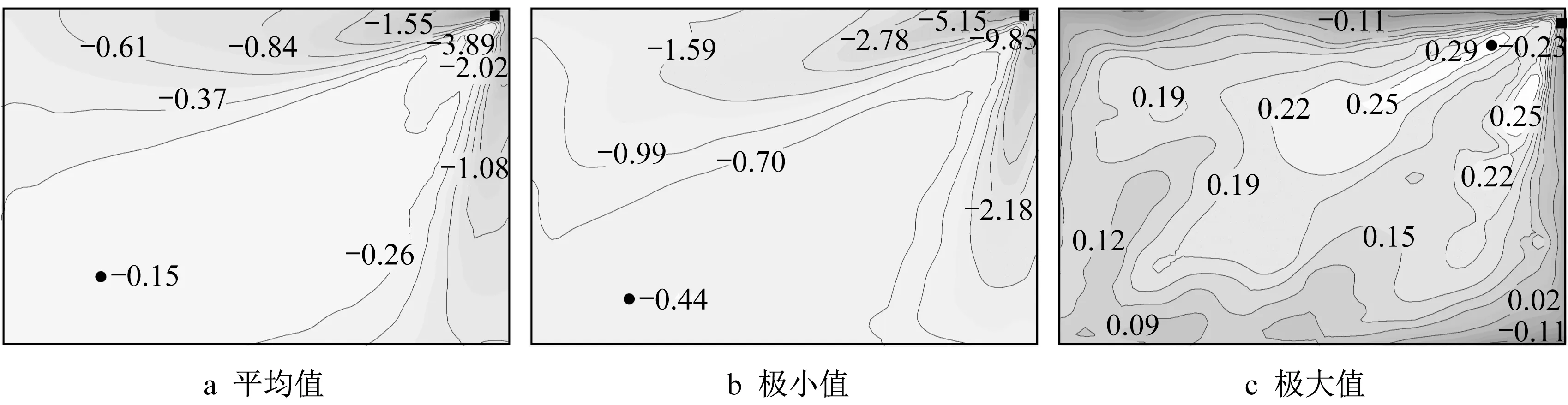
图9 45°风向角风压系数分布Fig.9 Distribution of wind pressure coefficients at 45°wind direction angle

3.2 相对位置的影响

图10为0°风向角下位于不同径向位置时屋面1/4区域（见图3）的风压系数对比。为了便于比较，选取“最佳剖面”位置的结果作为参照对象进行对比。由图10可见，“最佳剖面”位置与其他径向位置风压系数的点对点比较结果基本都分布在斜率为1的直线附近，这表明模型区内平均风压系数和极值风压系数在所研究的径向位置范围内变化相对不明显。

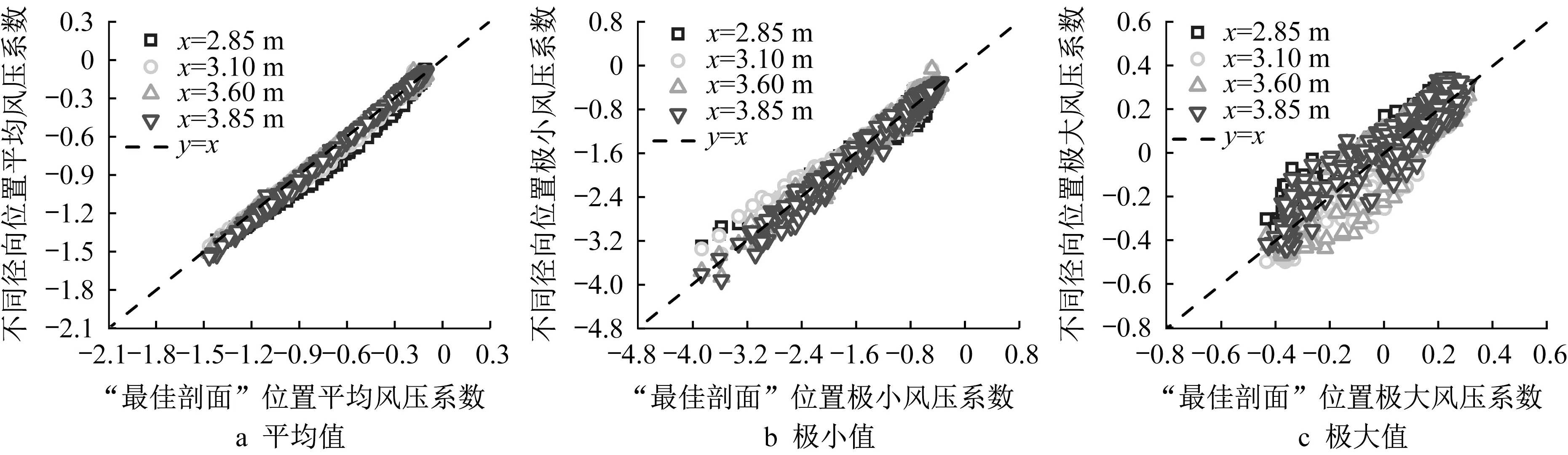
图10 不同径向位置的风压系数对比Fig.10 Comparison of wind pressure coefficients at different radial positions

3.3 和B类地貌试验结果的对比

进一步将以上结果和B类地貌的结果进行比较。为保证比较的客观性，参考风压的取值高度同样取为屋面高度40 m处，使得相同高度处风速相等。选取“最佳剖面”位置的结果作为参照对象，2个试验的参数如模型、风向角定义、采样设定等均保持一致。

3.3.1 平均风压系数

为了考察不同流场对屋面平均风压系数分布的影响，同样采取点与点间全面比较的方法，将不同流场中0°、45°和90°共3个风向角下每个测压点的平均风压系数进行逐一比较，结果如图11所示。

由图11可知，下击暴流风场和B类地貌常态风场作用下，大跨度平屋盖建筑模型各个测点的平均风压系数的测试结果非常接近，在整体上数据关联性强。因此，从平均风压系数的角度去分析，下击暴流和B类地貌流场的试验结果基本一致，说明下击暴流作用下大跨度平屋盖结构设计过程中的平均风荷载取值能够直接参照《建筑结构荷载规范》的体型系数。

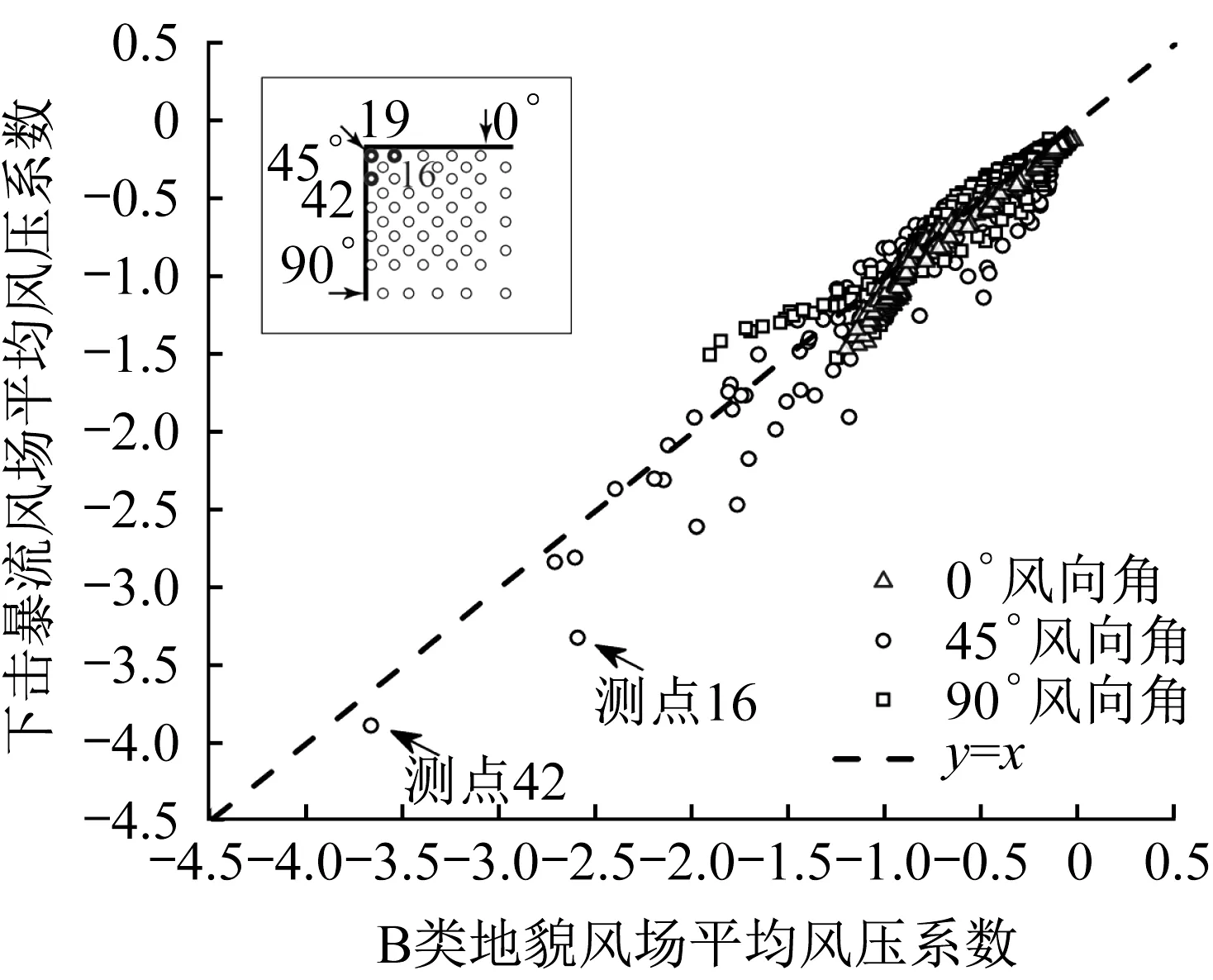
图11 不同风场下平均风压系数对比Fig.11 Comparison of mean wind pressure coefficients in different wind fields

3.3.2 极小风压系数

同样对2种风场作用下的屋面极小风压系数用点对点的方式进行对比，结果如图12所示。由图12可见，在下击暴流作用下，0°、45°和90°风向角在屋盖角区的极小风压系数绝对值最大值由B类地貌下的2.31、5.54、3.04相应地变为3.87、9.85、3.84，整体上由5.54升高到9.85，提高了77.8%。

图12 不同风场下极小风压系数对比Fig.12 Comparison of minimum wind pressure coefficients in different wind fields

整体而言，在0°、45°、90°风向角下，下击暴流风场的屋面吸力系数绝对值约为B类地貌相应结果的1.31倍、1.75倍和1.24倍，可见下击暴流风场的屋面吸力系数绝对值要整体高于B类地貌风场的吸力系数绝对值。如图13所示，从频域角度分析可知，下击暴流作用下屋面典型测点42号（见图3）的风压系数功率谱能量要整体高于B类地貌风场的结果。从结构安全的角度出发，在大跨度平屋盖建筑结构的设计过程中建议考虑下击暴流的作用，并提高角部等风敏感区域的抗风性能。图13中，Sc(f)为风压系数功率谱。

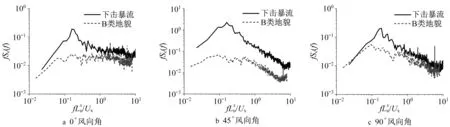
图13 测点42的风压系数谱Fig.13 Wind pressure coefficient spectrum at measuring point 42

3.3.3 极大风压系数

屋面存在的正压会对屋面整体承载力产生较大的影响，虽然模型屋面的平均风压系数和极小风压系数均为负值，但是仍然要关注极大风压系数的分布特征，确认其是否存在大于0的正压情况。图14为不同风场下屋面极大风压系数的分布情况。由于极大风压系数是在屋面受压的情况下考虑，因此仅需比较不同风场下屋盖极大风压系数的正值部分。

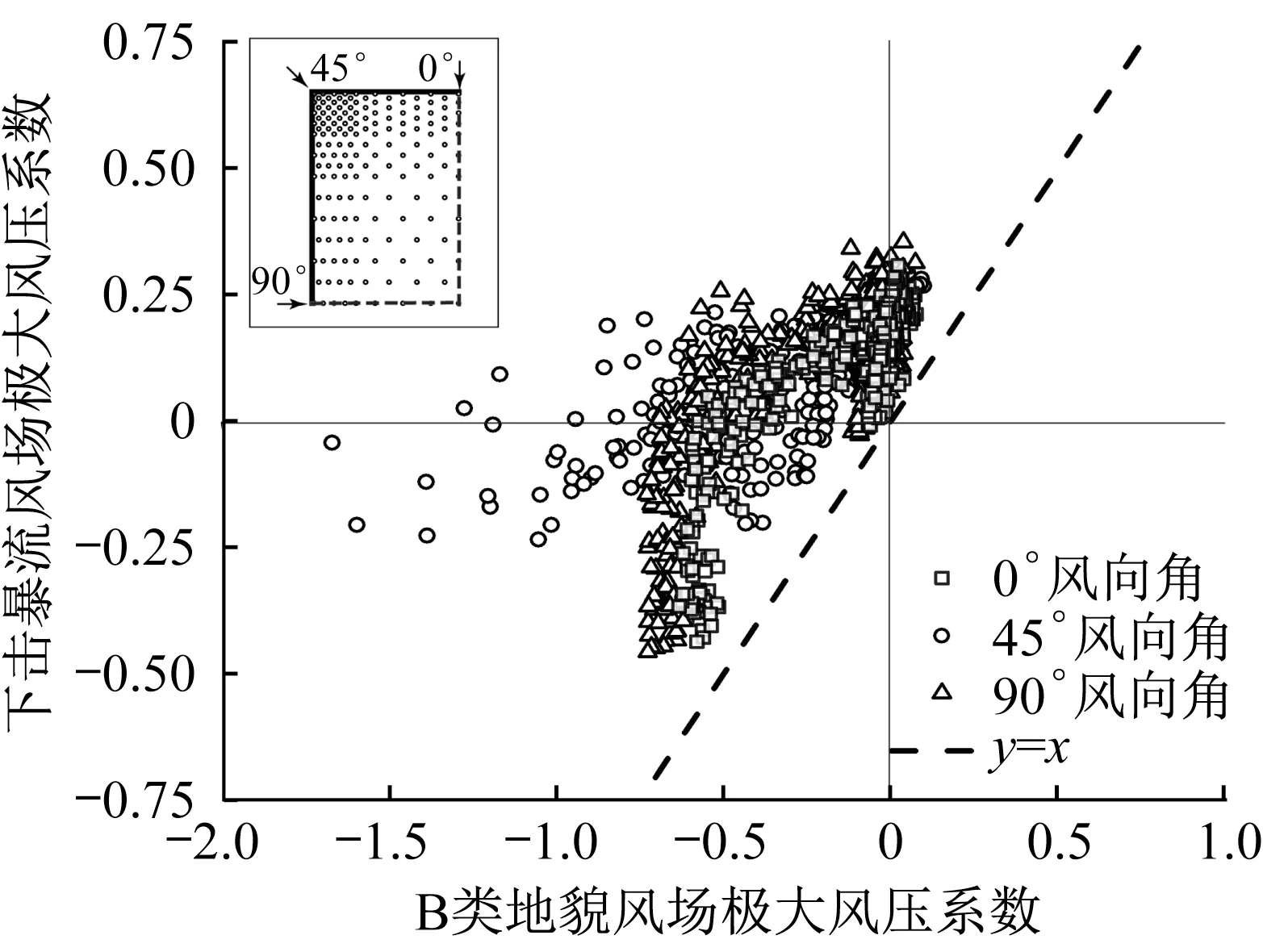
图14 不同风场下极大风压系数对比Fig.14 Comparison of maximum wind pressure coefficients in different wind fields

由图14可知，风压系数在第三象限皆为负值，此情况可不予讨论。在第二象限时，下击暴流作用下的极大风压系数为正值，而在B类风场作用下为负值，并且由于第四象限无风压系数分布，因此可以推断下击暴流风场比B类地貌风场对平屋盖造成更大的受正压面积；在第一象限时，不同风场下的极大风压系数都是正值，并且下击暴流风场作用下的极大风压系数远大于B类地貌风场作用下的相应值，这意味着下击暴流风场对平屋盖产生的正压力明显高于B类地貌风场。

结合图7和图12进一步分析发现，在不同风向角下，下击暴流作用下高于0.15的极大风压系数所占屋盖面积的比例范围处于51%到75%之间，极大风压系数局部最高可达0.35。这是由于下击暴流风场在近地表面的分布较为紊乱，除了水平方向的风速分量外还存在竖直向下的风速分量，会对屋面产生较强正压，而B类地貌常态风只有水平方向的分量，对模型表面产生的正压力极小。大范围的较高正压进一步影响结构的承载力，应在结构设计时引起注意。