自旋运动对射弹入水空化及弹道特性的影响
2022-01-15何思澈古鉴霄
何思澈, 罗 凯, 黄 闯, 古鉴霄, 任 鑫
自旋运动对射弹入水空化及弹道特性的影响
何思澈1, 罗 凯1, 黄 闯1, 古鉴霄1, 任 鑫2
(1. 西北工业大学 航海学院, 陕西 西安, 710072; 2. 山西平阳重工机械有限责任公司, 山西 侯马, 043001)
无尾翼超空泡射弹由舰载火炮发射, 出管后通过高速自旋维持空中弹道稳定, 用于对抗鱼雷、蛙人等水下目标。为研究自旋运动对超空泡射弹入水过程空化及运动特性的影响, 基于多相流模型和重叠网格技术建立了适用于射弹小角度高速自旋入水工况的数值模型, 对旋转射弹及无旋射弹以不同姿态入水的超空化流场及流体动力特性进行仿真计算。结果表明: 所建模型对于入水载荷、旋转横滚力矩、入水空泡的仿真结果均与实验结果吻合; 入水初期自旋运动可以促进自然空化的发生, 空泡呈现不对称特性; 自旋运动对射弹入水质心运动规律无显著影响; 自旋运动会减小射弹俯仰角变化, 有利于维持射弹入水纵平面稳定性。
超空泡射弹;自旋运动; 入水; 空化特性
0 引言
依托机/舰载火炮发射的超空泡射弹可高效防御鱼水雷、蛙人、无人水下航行器等小型水下目标的攻击。为了实现有效毁伤, 超空泡射弹必须具有稳定的空中、入水和水下弹道。就维持空中弹道稳定而言, 主要有2种设计思路: 1) 采用滑膛火炮发射尾翼弹; 2) 采用线膛炮发射无尾翼自旋弹。无尾翼自旋弹依靠陀螺力矩维持空中弹道稳定, 有效弥补了尾翼弹阻力系数大、丰满度小等缺点, 是一种非常有潜力的超空泡射弹设计方案[1]。然而, 自旋运动对射弹的入水运动特性也会产生一定影响。此外, 自旋射弹入水流场涉及自由液面、湍流、相变等复杂流动问题, 是超空泡武器应用研究的难点。
近年来, 国内外学者针对超空泡射弹入水问题做了大量实验和数值仿真研究。May等[2]对各种头型射弹垂直入水及倾斜入水做了大量实验, 根据实验数据提出了预测射弹入水空泡尺寸和形状的方法; Tassin等[3]建立了二维楔形体入水数值模型, 对入水空泡形成初期时楔形体受到的瞬态阻力进行了估算; Mclntyre等[4]采用浸没边界法对三维圆柱体高速入水过程进行了仿真, 并将仿真得到的空泡外形与实验空泡外形进行了对比; Erfanian等[5]对球头超空泡射弹入水问题进行了数值仿真和实验研究, 仿真得到的空泡外形及弹丸弹道与实验结果吻合较好; 顾建农等[6]对球形弹丸旋转入水问题进行了实验研究, 给出了弹丸水中速度衰减规律的数学预报模型; 肖海燕等[7]运用数值方法研究了高速旋转射弹小角度入水过程中的空化现象和弹体运动规律; 李佳川等[8]建立了射弹入水单平面运动的动力学模型, 研究了初始扰动角速度对射弹入水弹道的影响; 王泽宇[9]指出为保持超空泡射弹航行过程的稳定性, 可以让射弹在航行过程中具有自旋角速度或者将航行器尾部形成尾翼结构。
上述文献表明, 自旋超空泡射弹具有稳定的空中弹道, 但由于其入水流场更加复杂, 给入水弹道的稳定性带来新的问题。当前对旋转射弹入水流场的研究大多在无旋或低速自旋的条件下开展。对于高速射弹自旋入水问题, 实验难度大, 且获得的有效实验数据非常有限; 采用数值仿真的方法可以充分获得流动规律和流体动力特性, 进而揭示入水弹道稳定性的本质。然而目前尚未发现关于射弹高速自旋入水的数值模型和仿真方法的报道。为研究高速自旋运动对超空泡射弹入水运动及空化特性的影响, 文中建立了无尾翼射弹高速入水数值模型, 并从入水冲击载荷、旋转横滚力矩和入水空泡3个方面对模型的计算精度进行了验证, 在自旋角速度20 000 r/min条件下对超空泡射弹开展入水流场的数值仿真研究, 评估了自旋运动对无尾翼射弹入水过程空化特性及弹道特性的影响。
1 数值模型建立
超空泡射弹入水流场涉及自由液面、湍流和相变等复杂流动问题, 通过实验获得射弹入水的运动和空化特性存在很大的难度。采用计算流体力学(computational fluid dynamics, CFD)的方法, 联合多相流模型、湍流模型和刚体运动方程组, 建立了高速自旋射弹入水流场数值计算模型。
1.1 几何外形
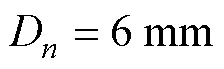
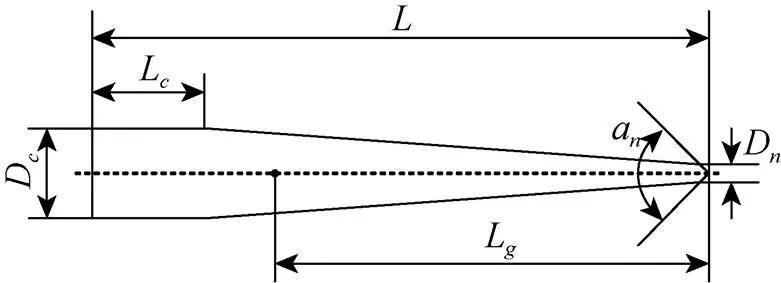
图1 射弹几何外形
1.2 控制方程
1) 连续性方程
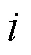
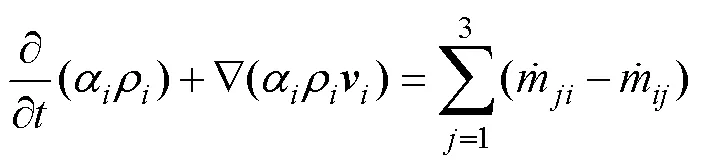
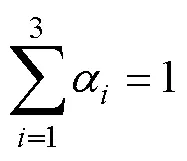
2) 动量方程
VOF多相流模型描述混合流动系统的动量方程为
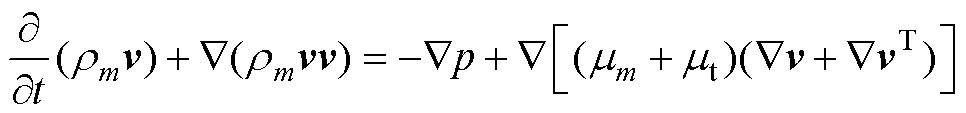
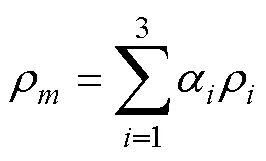
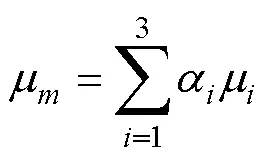
3) 湍流模型

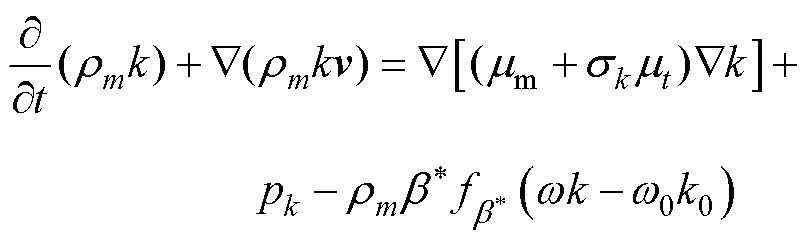
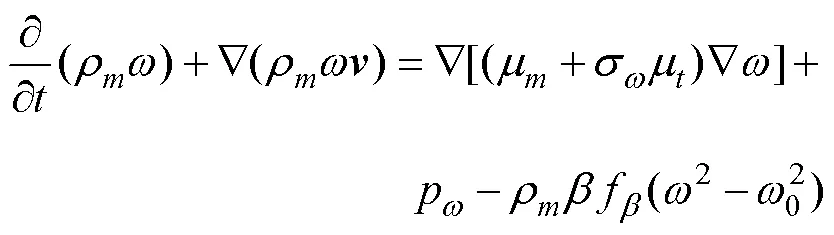
4) 空化模型
射弹高速入水时会发生空化现象, 当流场静压低于水饱和蒸气压时液态水会蒸发形成水蒸气, 反之水蒸气会凝结形成液态水。采用Schnerr- Sauer空化模型[12]描述射弹入水时的空化过程, 该模型对于汽液相间的质量传输描述如下。
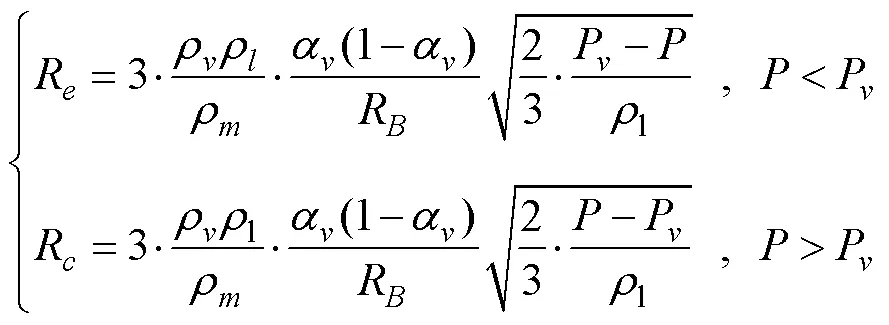
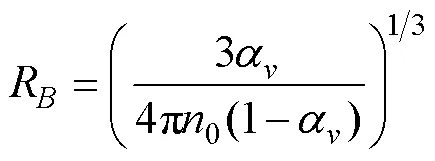
5) 刚体运动方程

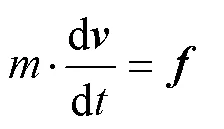
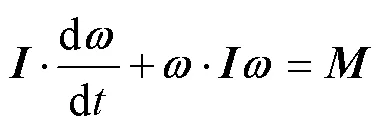
仿真过程中将上一时刻流场计算所得流体动力特性带入刚体运动方程组, 获得射弹运动状态以及当前时刻的位置和姿态参数; 网格解算器根据射弹的位置和姿态变化重构并更新计算域网格; 流场求解器使用更新后的网格, 考虑射弹运动参数的变化, 计算射弹当前时刻的流体动力特性。如此反复迭代, 可实现射弹高速入水流场与运动的耦合仿真。
1.3 边界条件及网格划分
边界条件设置如图2所示。定义射弹在入水初始时刻弹轴与水平面的夹角为入水角, 射弹的初始速度为600 m/s方向沿弹轴向下, 射弹的自旋角速度为20 000 r/min, 重力方向铅锤向下。计算域上侧边界和下侧边界分别设置为压力入口和压力出口, 入口总压为101325 Pa, 出口静压为静水压; 计算域左、右两侧边界设置为速度入口, 速度为0。无旋射弹计算模型的边界条件采用与图2相同的设置, 仅将初始旋转速度设置为0。

图2 计算域设置
采用重叠网格技术建立自旋射弹入水数值模型, 射弹周围为重叠网格区域, 整个计算域为背景区域, 通过“挖补”处理, 实现重叠区域在背景区域内的自由运动。为精确模拟射弹周围流场以及射弹入水受力情况, 对重叠网格区域、射弹行进区域以及气液交界面附近网格进行加密处理。为保证仿真结果的独立性, 需要进行网格无关性验证。针对计算模型分别采用103万、207万、410万网格进行仿真计算, 计算工况均为入水速度600 m/s, 自旋速度20 000 r/min, 入水角7°。提取射弹入水过程中横滚力矩变化情况进行对比, 发现103万网格计算结果明显小于207万网格, 207万网格计算结果与410万网格无明显差异, 如图3所示, 说明207万网格能同时满足计算精度和计算效率的要求。最终网格划分情况如图4所示。
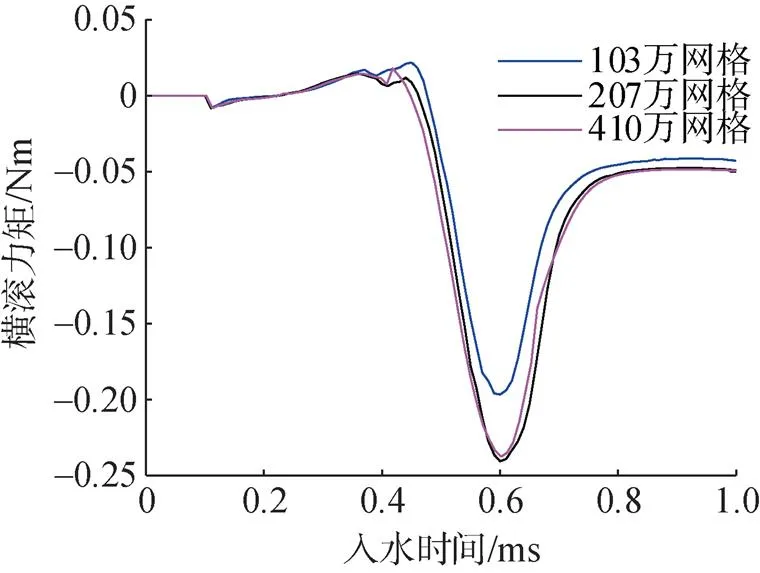
图3 不同网格数量横滚力矩对比
1.4 模型验证
陈诚等[13]针对超空泡航行器入水问题进行了实验研究, 得到超空泡航行器小角度入水轴向载荷。采用文中所建立的数值模型, 对文献中航行器入水实验过程进行数值仿真, 得到实验模型入水过程中轴向载荷随时间的变化关系, 如图5所示, 由图可知, 仿真得到的轴向载荷变化情况与实验测试的结果一致, 最大相对偏差不超过9.7%。
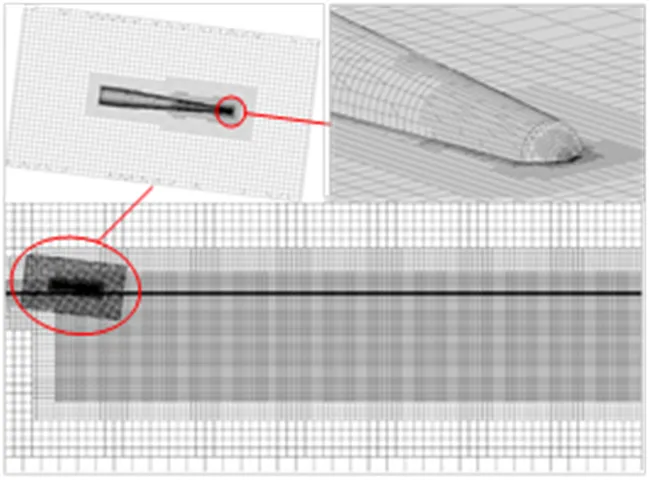
图4 计算域网格划分

图5 入水轴向载荷实验与仿真结果对比
高善群[14]针对水中高速旋转圆柱转子阻力特性进行了实验研究, 提出了水下转子自旋摩擦力矩计算经验公式。采用文中建立的数值模型, 对射弹在水下高速自旋运动进行数值仿真, 得到射弹在不同转速下受到的横滚力矩并与经验公式计算得到的结果进行对比, 如图6所示。对比结果显示, 仿真得到的射弹横滚力矩结果与经验公式计算结果一致, 最大相对偏差为9.1%。
郭子涛[15]针对细长圆柱体的高速入水问题进行了实验研究, 得到了不同外形细长体的入水空化情况。实验模型的尺寸为12.65 mm×25.4 mm, 模型材质为38CrSi钢, 以603 m/s的初速度垂直于自由面入水。采用文中所建立的数值模型, 对文献[15]的实验过程进行数值仿真, 得到模型入水后的空泡外形如图7所示。如图所示, 不同时刻实验观测点处空泡半径与数值仿真结果吻合较好, 观测点基本位于仿真得到的空泡轮廓线上。
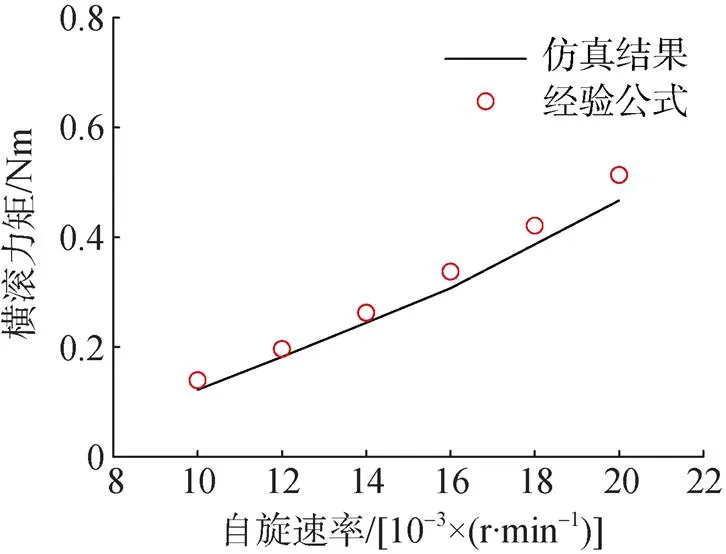
图6 横滚力矩实验与仿真结果对比
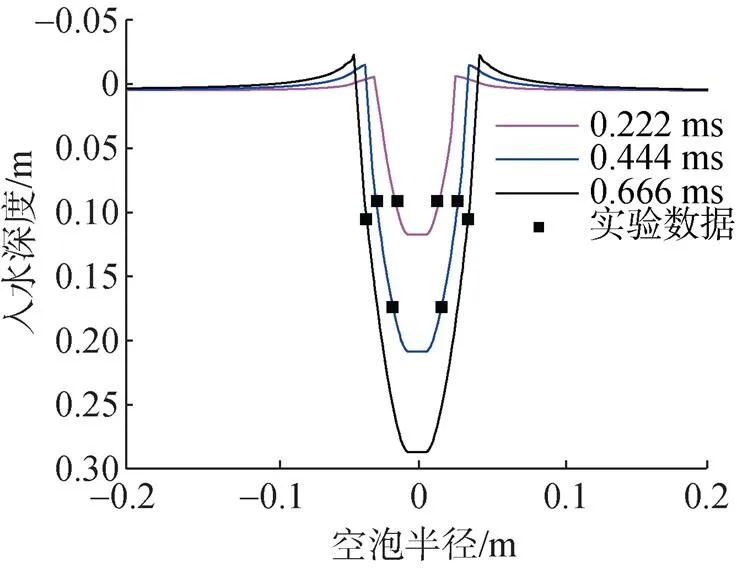
图7 入水空泡外形仿真与实验结果对比
综上所述, 文中所建模型在模拟高速自旋射弹入水时, 对于入水冲击载荷、旋转横滚力矩、入水空泡形态的仿真结果均与实验结果吻合。
2 射弹入水空化特性仿真
2.1 无旋入水空化流动及超空泡流型特性
提取射弹7°入水时在纵截面处流场的多相流特性, 如图8所示。射弹入水偏航角变化最大值相比俯仰角小了2个数量级, 流场相对于纵截面近似对称。射弹入水初期空化器下侧先与水面接触, 弹体下侧空泡内充满了水蒸气, 上侧空泡内也含有大量水蒸气和少量射弹入水携入的空气, 两侧蒸气分布呈现出不对称性, 上侧蒸气多于下侧。出现这种现象是因为在入水初期空泡会在弹体下侧闭合而在上侧敞开, 空化器产生的水蒸气在开口泡内充分发展。射弹行进至2倍弹长时, 射弹上侧的水蒸气充分发展, 弹体周围水蒸气对称分布, 形成包裹住弹体全身的超空泡。
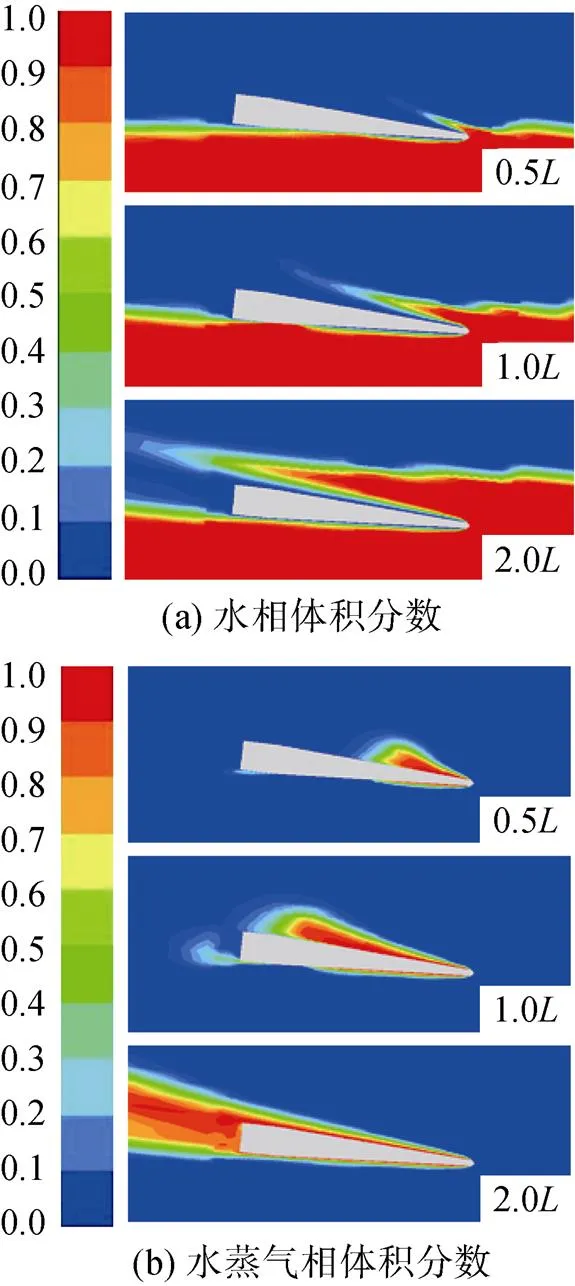
图8 射弹无旋入水流场多相流特性
以计算域水相体积分数为0.5的等值面表征空泡壁面, 获得无尾翼射弹无旋入水空泡演变过程如图9所示。射弹入水后撞击自由液面形成不对称的空泡, 下侧空泡发展快于上侧。在射弹行进了1倍弹长后, 空化器产生的空泡未能完全覆盖住射弹尾部, 弹体上下两侧空泡呈现不对称性, 使射弹尾部部分沾湿, 沾湿区域基本对称分布; 随后空泡迅速发展, 包裹住射弹全部弹身。射弹入水角为15°、30°时多相流特性类似, 不再赘述。
2.2 旋转入水空化流动及超空泡流型特性
提取射弹以7°入水角旋转入水及无旋入水时纵截面水蒸气相轮廓线, 对比射弹入水0.5及2时水蒸气相分布, 如图10所示。以弹长为参考对空泡轮廓进行无量纲化, 自由液面的初始位置位于直线=0上。通过对比分析, 发现旋转入水初期水蒸气发展更充分, 表明自旋运动促进了射弹入水自然空化现象。
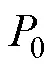

图9 射弹无旋入水空泡形态
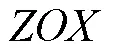
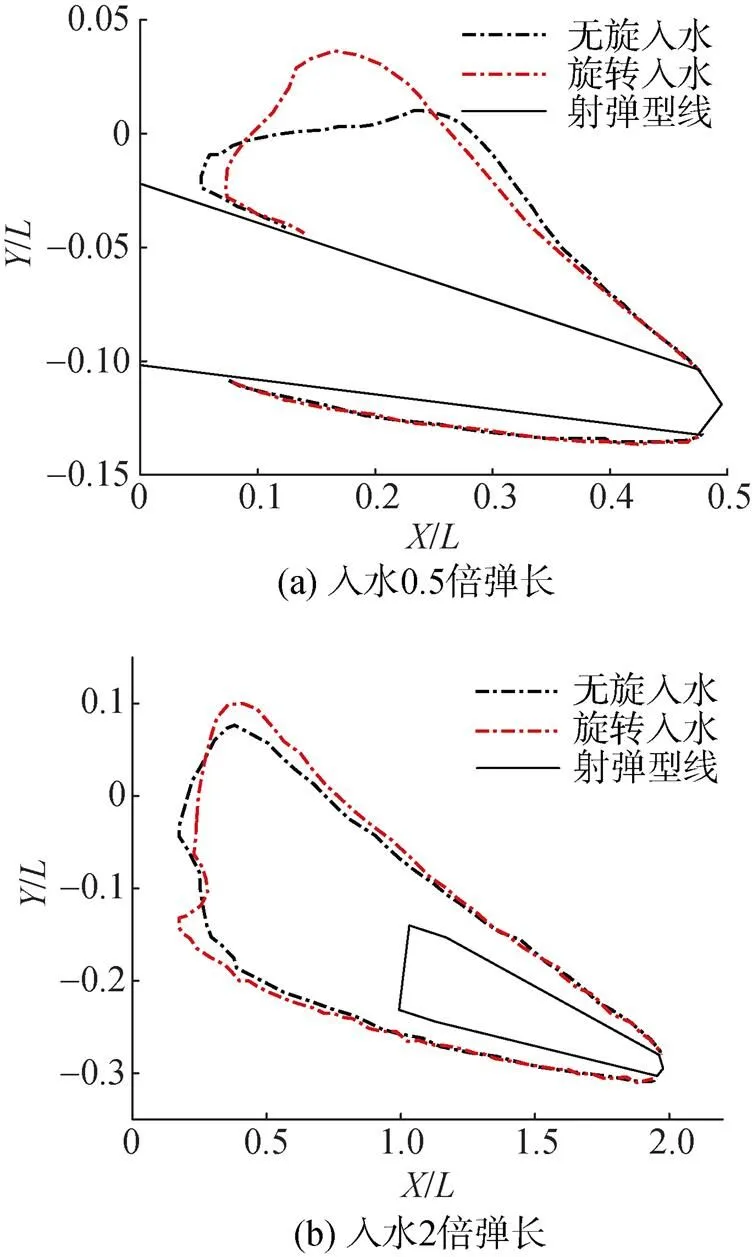
图10 纵截面处射弹周围水蒸气相轮廓
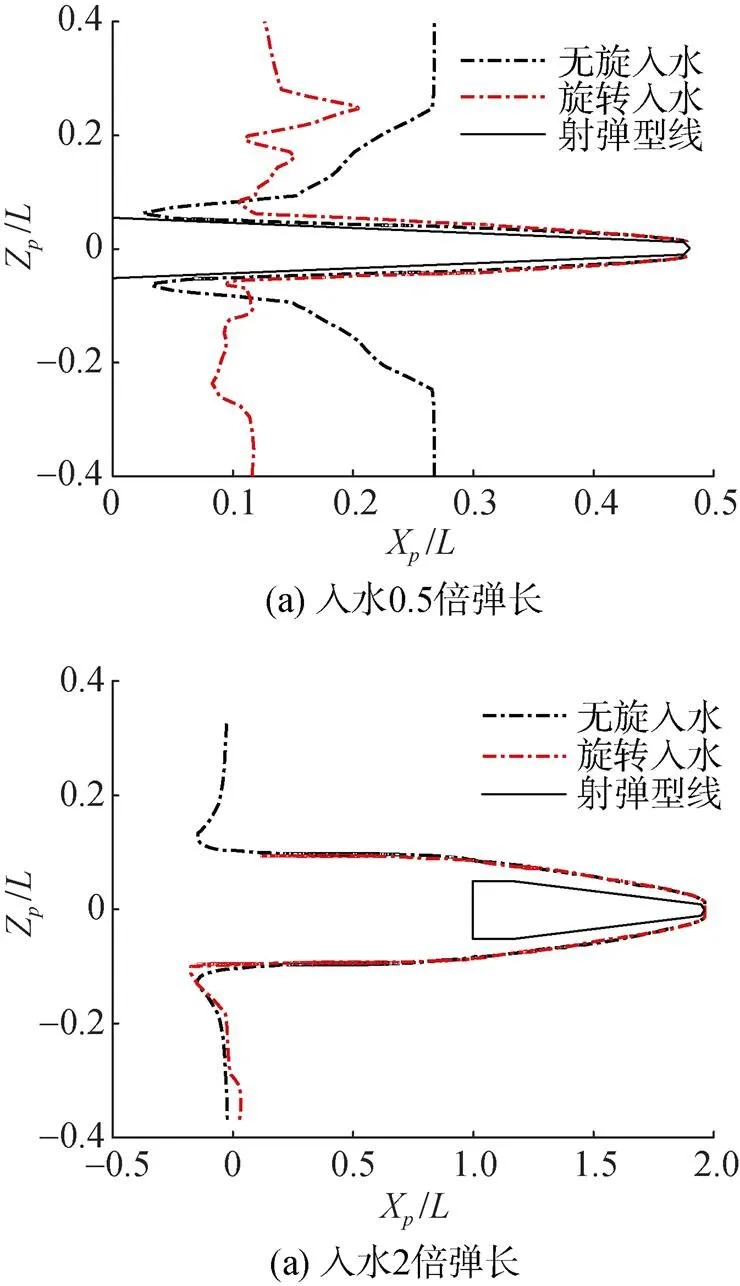
图11 P0截面处射弹周围空泡轮廓
图12 P0截面位置示意图
Fig. 12 Location of section P0
图13 入水1倍弹长弹体尾部沾湿情况
3 仿真与分析
3.1 射弹入水运动特性
图14给出了射弹在7°、15°和30°入水角下旋转入水及无旋转入水时质心在纵平面上的运动轨迹, 在各入水角下射弹均基本保持直线运动, 且旋转射弹与无旋射弹纵平面运动弹道基本重合, 7°入水的射弹方向位移达到2倍弹长时方向位移仅相差0.3%。进一步分析对比发现, 自旋运动对射弹入水水平面弹道也几乎没有影响, 说明自旋运动对射弹入水弹道的影响较小。
对比分析射弹在上述工况下入水时弹体方向及方向速度衰减曲线, 如图15所示。射弹入水后速度缓慢衰减, 在各入水角下旋转入水及无旋入水速度变化情况基本一致。射弹30°入水2倍弹长时方向速度幅值仅相差0.1%,方向速度幅值仅相差0.9%, 进一步说明自旋运动对射弹入水位置特性影响较小。
图16给出了射弹在7°、15°和30°入水角下入水时俯仰角变化情况。射弹小角度入水时锥型空化器下表面先与水面接触, 弹体头部受到抬头力矩, 使得射弹入水后俯仰角以及俯仰角速度持续增大。对照射弹入水空泡形态图(见图9)可知,当射弹行进至柱段经过水平面时, 空泡未能发展至完全包裹弹体, 尾部沾湿产生恢复力矩, 弹体俯仰角速度在达到峰值后略微下降。此后空泡完全发展, 射弹尾部不再沾湿, 弹体俯仰角速度缓慢上升。此外自旋运动对射弹入水时俯仰角变化有明显的抑制作用, 射弹在7°、15°和30°旋转入水2倍弹长时俯仰角峰值分别减小44.3%、45.3%和47.5%, 俯仰角速度峰值分别减小42.5%、53.2%和59.2%, 说明自旋运动提升了射弹入水时纵平面运动的稳定性。以上结论将在射弹入水流体动力特性曲线中得到验证。
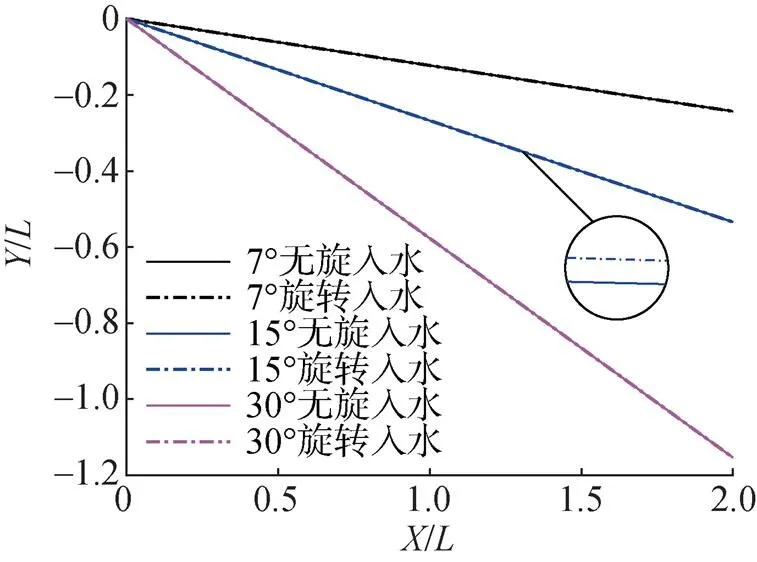
图14 射弹入水质心纵平面位移
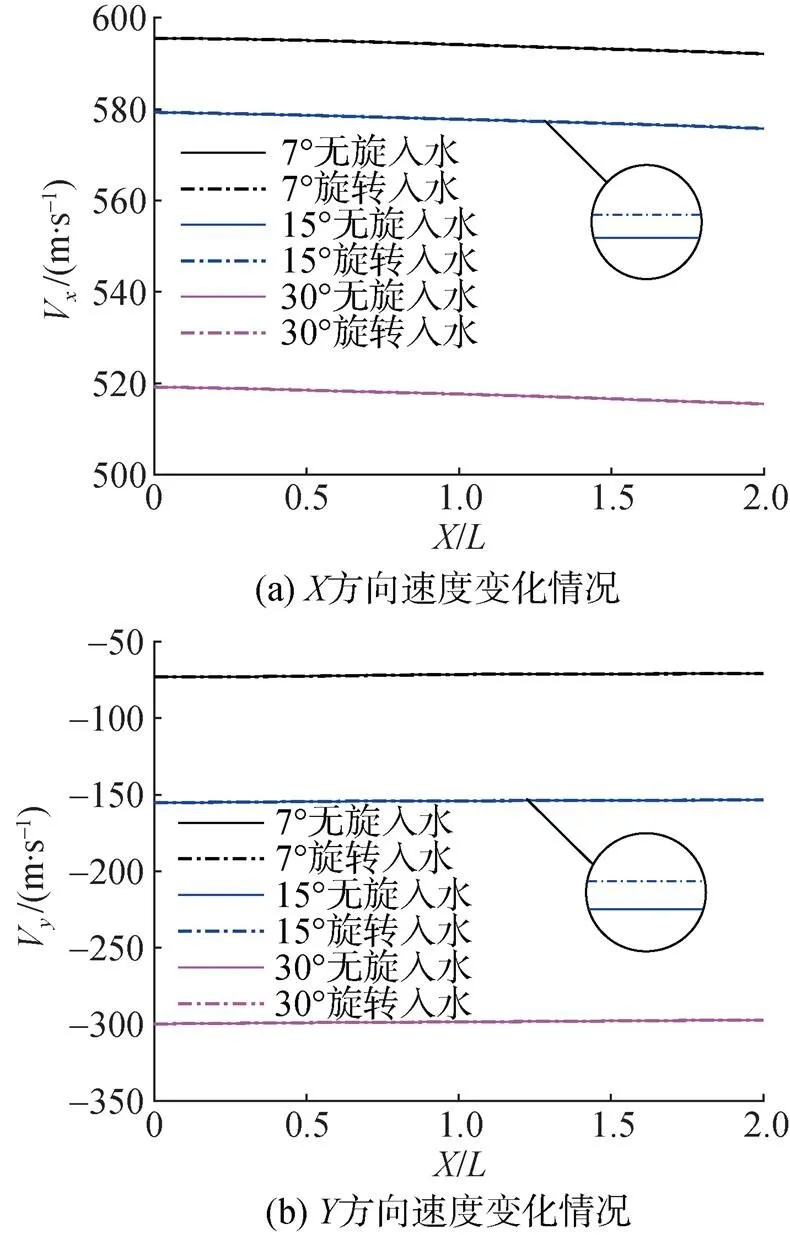
图15 射弹入水速度变化情况
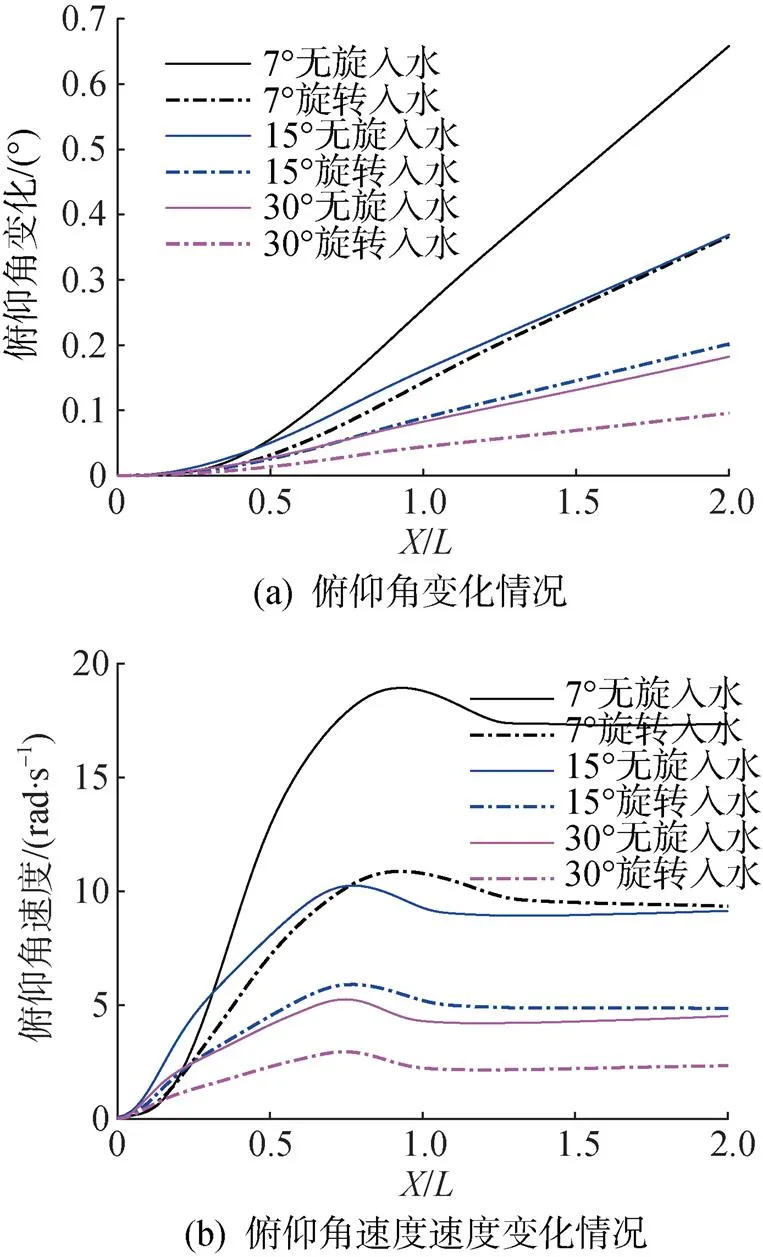
图16 射弹入水俯仰角变化情况
3.2 射弹入水流体动力特性
射弹入水过程中, 受力的变化是导致其运动特性变化的根本原因。为分析自旋运动对无尾翼射弹入水受力的影响, 定义无量纲流体动力系数
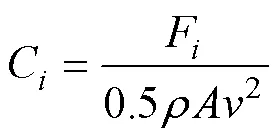
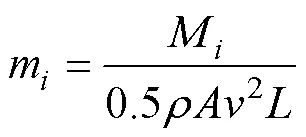
射弹无旋、有旋入水过程中的阻力特性变化如图17所示。射弹入水后空化器与自由液面接触, 阻力系数迅速上升; 此后弹体尾部掠水, 阻力系数继续增大; 随着入水深度的增加, 自然空化区域不断增大形成覆盖弹体的超空泡, 射弹阻力系数逐渐减小并趋于稳定。射弹入水后阻力主要来源于沾湿表面, 射弹的自旋未引起沾湿面积的显著变化, 因此对阻力系数没有明显影响。
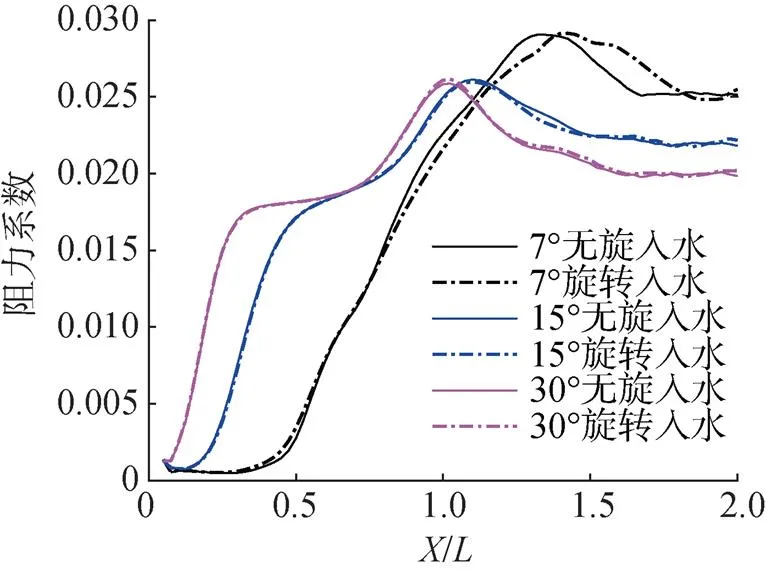
图17 射弹入水阻力系数变化情况
图18给出了无尾翼射弹无旋入水及旋转入水过程中俯仰力矩系数及横滚力矩系数变化情况。
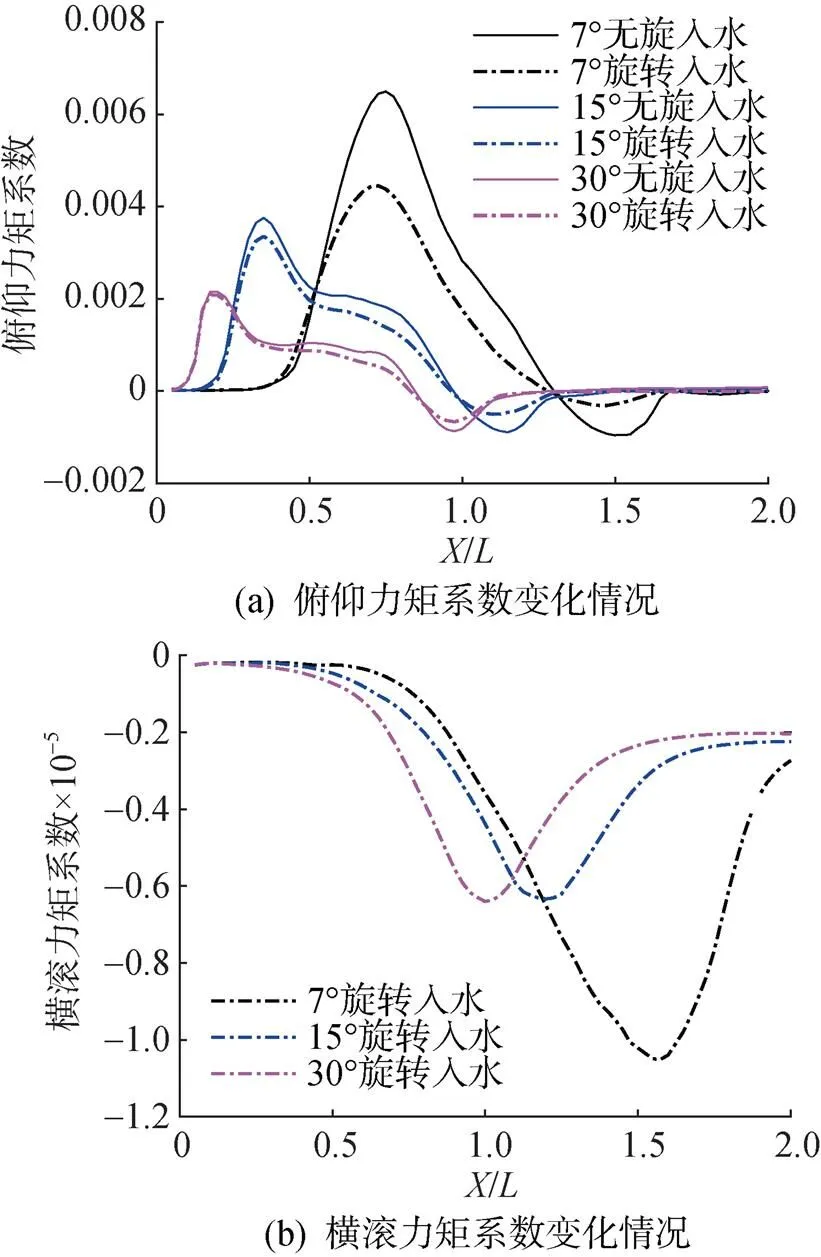
图18 射弹入水力矩系数变化情况
如图所示, 射弹小角度入水时空化器下表面与自由液面接触, 弹体受到抬头力矩的作用, 弹体俯仰力矩系数持续上升; 空化器受到周向摩擦力作用, 弹体横滚力矩系数略微上升。射弹行进至尾部掠水时, 弹体柱段沾水产生恢复力矩, 弹体俯仰力矩系数减小至反向, 弹体横滚力矩系数迅速上升。超空泡完全覆盖弹体后, 弹体仅有空化器沾湿, 俯仰力矩系数和横滚力矩系数均下降至0附近。旋转射弹与空泡壁接触时动能会传递给水相, 相比无旋入水时弹体尾部沾湿部分动压增大而静压减小, 弹体受到的由压差产生的恢复力减小, 俯仰力矩系数变化幅度削弱。
4 结论
文中建立了无尾翼射弹入水数值仿真模型, 对比分析了自旋运动对文中指定外形的无尾翼射弹入水空化特性以及弹道特性的影响, 主要得到以下结论。
1) 建立了适用于射弹小角度高速自旋入水工况的数值模型, 可模拟射弹入水过程中的超空泡流型、流体动力特性和弹道特性。
2) 自旋运动对射弹入水空泡流型的影响随着入水深度的增加而减小, 自旋射弹入水初期水蒸气相发展更加充分, 空泡流形不对称性更加明显。
3) 自旋运动对射弹入水位置特性影响较小, 对弹体俯仰角以及俯仰角速度变化有抑制作用, 有利于射弹纵平面弹道的稳定。
[1] 姚忠, 王瑞, 徐保成. 超空泡射弹火炮武器应用现状研究[J]. 火炮发射与控制学报, 2017, 38(3): 92-96.
Yao Zhong, Wang Rui, Xu Bao-cheng. Research on Current Application State of Supercavitation Projectile Artillery Weapons[J]. Journal of Gun Launch & Control, 2017, 38(3): 92-96.
[2] May A. Water Entry and the Cavity-Running Behavior of Missiles[R]. NASA: NASA Sti/recon Technical Report N, 1975.
[3] Tassin A, Korobkin A A, Cooker M J. On Analytical Models of Vertical Water Entry of a Symmetric Body with Separation and Cavity Initiation[J]. Applied Ocean Research. 2014, 48: 33-41.
[4] Mcintyre S, Kinzel M, Miller S, et al. The Immersed Boundary Method for Water Entry Simulation[C]//49th Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition. Florida, USA: AIAA, 2011.
[5] Erfanian M R, Anbarsooz M, Rahimi N, et al. Numerical and Experimental Investigation of a Three Dimensional Spherical-nose Projectile Water Entry Problem[J]. Ocean Engineering, 2015, 104: 397-404.
[6] 顾建农, 张志宏, 范武杰. 旋转弹丸入水侵彻规律[J]. 爆炸与冲击, 2005, 25(4): 341-349.
Gu Jian-nong, Zhang Zhi-hong, Fan Wu-jie. Experimental Study on the Penetration Law for a Rotating Pellet Entering Water[J]. Explosion and Shock Waves, 2005, 25(4): 341-349.
[7] 肖海燕, 罗松, 朱珠, 等. 高速射弹小角度入水弹道特性研究[J]. 北京理工大学学报, 2019, 39(8): 784-791.
Xiao Hai-yan, Luo Song, Zhu Zhu, et al. Trajectory and Cavitation Characteristics of High-Speed Projectiles at Small Angle of Water Entry[J]. Transactions of Beijing Institute of Technology 2019, 39(8): 784-791.
[8] 李佳川, 魏英杰, 王聪, 等. 不同扰动角速度高速射弹入水弹道特性[J]. 哈尔滨工业大学学报, 2017, 49(4): 131-136.
Li Jia-chuan, Wei Ying-jie, Wang Cong, et al. Water Entry Trajectory Characteristics of High-speed Projectiles with Various Turbulent Angular Velocity[J]. Journal of Harbin Institute of Technology, 2017, 49(4): 131-136.
[9] 王泽宇. 旋转超空泡射弹流体动力特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
[10] Smolarkiewicz P K. Application of the Volume-of-Fluid Method to the Advection-Condensation Problem[J]. Monthly Weather Review, 1997, 125(9): 2265-2273.
[11] Wilcox D C. Formulation of the-Turbulence Model Revisited[J]. AIAA Journal, 2008, 46(11): 2823-2838.
[12] Habil S I. Physical and Numerical Modeling of Unsteady Cavitation Dynamics[C]//4thInternational Conference for Multiphase Flow. New Orleans, USA: ICMF, 2001.
[13] 陈诚, 袁绪龙, 党建军, 等. 超空泡航行器20°角倾斜入水冲击载荷特性试验研究[J]. 兵工学报, 2018, 39(6): 1159-1164.
Chen Cheng, Yuan Xu-long, Dang Jian-jun, et al. Experimental Investigation into Impact Load during Oblique Water-entry of a Supercavitating Vehicle at 20°[J]. Acta Armamentarii, 2018, 39(6): 1159-1164.
[14] 高善群. 液体中圆柱转子旋转运动的阻力研究[D]. 洛阳: 河南科技大学, 2013.
[15] 郭子涛. 弹体入水特性及不同介质中金属靶的抗侵彻性能研究[D]. 哈尔滨: 哈尔滨工业大学, 2012.
Effect of Spinning Motion on Cavitation and Trajectory Characteristics of Projectile during Water Entry
HE Si-che1, LUO Kai1, HUANG Chuang1, GU Jian-xiao1, REN Xin2
(1. School of Marine Science and Technology, Northwestern Polytechnical University, Xi’an 710072, China; 2. Shanxi Pingyang Industry Machinery CO.LTD, Houma 043001, China)
A tailless supercavity projectile is launched by ship-borne artillery to kill underwater targets, such as torpedoes and frogmen, and the projectile spins at a high speed to maintain a stable trajectory in air. To study the effects of spinning on cavitation and trajectory characteristics of the projectile during water entry, a numerical model of the projectile flow field when entering water at a small angle and high spinning speed is established using the multiphase flow model and the overlapping grid technology. The supercavitation flow field and hydrodynamic characteristics of the spinning projectile and projectile without spinning motion entering water at different attitudes are calculated. The results show that the numerical models are in good agreement with the experimental results for the water entry load, rolling moment, and cavitation. The spinning motion promotes the occurrence of natural cavitation at the initial stage of water entry, the supercavity is asymmetric, and the spinning motion has no significant effect on the center of mass motion of the projectile during the water entry stage; the spinning motion restricts the pitch angle of the projectile, and is helpful in enhancing the horizontal motion stability.
supercavity projectile; spinning motion; water entry; cavitation characteristic
TJ630.1; O427.4
A
2096-3920(2021)06-0760-09
10.11993/j.issn.2096-3920.2021.06.017
何思澈, 罗凯, 黄闯, 等. 自旋运动对射弹入水空化及弹道特性的影响[J]. 水下无人系统学报, 2021, 29(6): 760-768.
2021-07-22;
2021-09-28.
国家自然科学基金资助项目(51909218); 中国博士后科学基金资助项目(2019M653747); 西北工业大学基础科研业务费资助项目(3102019HHZY030010).
何思澈(1997-), 男, 在读硕士, 主要研究方向为超空泡射弹及水下航行器总体设计.
(责任编辑: 许 妍)
