降雨对风力机翼型气动性能的影响

文 洮，陈春霖，王林柱，杨元娟

降雨对风力机翼型气动性能的影响

文 洮，陈春霖，王林柱，杨元娟

（甘肃省计算中心，甘肃 兰州 730030）

以NACA0012翼型为研究对象，采用拉格朗日离散相模型，研究在不同浓度雨滴下翼型气动性能的影响。研究发现：在降雨环境下，翼型表面会形成一定厚度的液膜，液膜的形成影响翼型表面的光洁度，引起边界层的提前转捩，造成翼型升力减小，阻力增大；翼型表面液膜随着计算时间的推移，翼型的压力面，主要是由于雨滴直接与翼型壁面发生碰撞而形成；翼型的吸力面，主要是由翼型前缘形成液膜后，再逐渐向尾缘流动而形成；当雨滴的浓度增大时，翼型表面形成液膜高度的波动更大，对于其升阻力的影响也将增大。

风力机；液膜高度；雨滴直径；气动性能；质量浓度

当风力机在降雨环境下运行时，翼型表面的多相流环境是十分复杂的。当雨滴与叶片表面接触碰撞时，一些较大的液滴将会发生破裂溅射出很多小液滴，这些小液滴与翼型边界层相互作用，就会造成气动性能的损失；而形成的有些小液滴将会附着于叶片表面形成水膜层，而形成之后雨滴的撞击就会在液膜表面形成凹坑和波纹，这将会严重影响翼型表面的光洁度，进而影响其气动性能。故研究降雨对风力机翼型气动性能的影响具有重要意义[1]。

近年来，为了更加清楚地了解翼型在降雨环境下对于气动性能的影响，研究者开始更加关注对降雨环境下翼型气动性能变化的机理性研究。Hsu[2]建立了降雨模型，研究了在降雨环境下翼型气动性能损失的主要影响原因，研究表明，雨滴在接触翼型前缘位置时，造成其升力明显减小，阻力明显增加。Valentine等[3]利用CFD模拟了在降雨环境下NACA 64-210翼型气动性能的影响，雨滴的溅射，液滴相之间相互的碰撞与聚合，都会造成翼型气动性能的损失。ALAN等[4]、Yeom G S等[5]在强降雨环境中的翼型实验发现，翼型在降雨环境下会造成严重的性能损失。Hansman等[6-7]研究了在降雨环境下翼型将会发生边界层的提前转捩，并且雨滴与气流之间存在很强的气流交换，导致翼型升力系数减小与阻力系数上升。Cai等[8]模拟研究在降雨环境下，S809翼型升力减小而阻力增加。Valakera等[9]、Cortés等[10]和Launder等[11]提出了液滴侵蚀保护涂层，并进行了测试。

本文选取了以NACA0012翼型作为研究对象，采用-湍流模型进行计算，结合真实的降雨环境，雨滴的直径并不是统一的，研究了在同一质量浓度下，不同雨滴直径下对于翼型的气动性能的影响，以及在同一雨滴直径、不同质量浓度对于翼型气动性能的影响。

1 数值方法

1.1 流场计算

计算采用SIMPLE算法来求解，边界条件选用无滑移边界；湍流模型选用-湍流模型来进行计算；该模型是由Launder和Spalding[11]提出的，其输运方程如下：

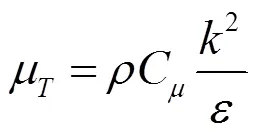
式中：为湍动能；为湍流耗散率。

式中：模型的封闭常数为1ε=1.44，2ε=1.92，C=0.09，σ=1.0，σ=1.3.

1.2 雨滴的降落速度

在降雨环境中，雨滴最开始降落时在受到重力的作用下将加速下落，但是，由于受到空气阻力的作用，使其加速到一定程度时，即达到阻力与重力相等，此时雨滴将匀速降落。这时，雨滴的速度就为雨滴的末速度，Markowitz[12]研究的表达式为：

式中：T为雨滴降落的最终速度，单位m/s；为雨滴直径，单位为mm。

1.3 DPM壁面液膜模型

离散相模型如图1所示，壁面液膜主要是由液滴与壁面接触、碰撞产生一系列物理现象形成。在壁面液膜模型中，主要是由以下几个部分组成：

(1)液滴与壁面边界撞击所造成的相互作用；

(2)液滴与壁面接触后的颗粒追踪；

(3)在壁面形成液膜后的高度计算以及气相与液相之间的耦合计算[13]。

液滴与壁面发生接触时，会发生一系列的相互作用：小液滴将会在壁面发生黏附现象，形成液膜；大液滴将会发生破碎，破碎后一些小液滴将会继续附着于壁面形成液膜，而另一部分将会发生反弹、飞溅等作用于流场中，并且大雨滴的碰撞也将会引起液膜流动的方向和速度变化。

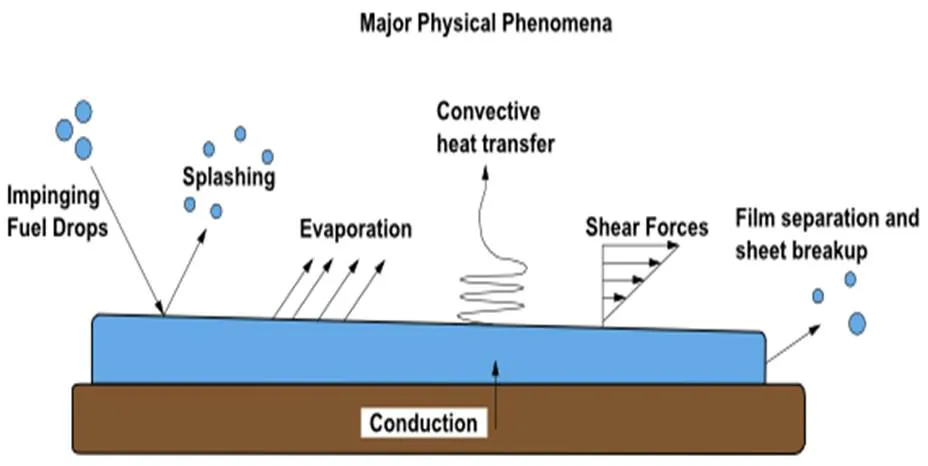
图1 壁面液膜模型

膜质量守恒方程和膜动量守恒方程，如式(4)、式(5)所示。

膜能量守恒方程如式(6)所示。

1.4 几何模型及网格划分

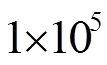
图2 计算区域

图3 翼型周围网格分布

2 计算结果分析

2.1 数值模拟方法验证

为了验证雨水建模的准确性，首先计算NACA0012翼型在雨水条件下的升力和阻力系数，并将结果与Hansman等[14]的实验结果进行比较，验证了标准-湍流模型。分别在清洁空气下和降雨环境下进行模拟，选取颗粒直径为1 mm，雷诺数为3.1×104，质量浓度为30 g/m3，求解过程中，速度和压力采用SIMPLEC算法，首先采用稳态计算，计算稳定后，再调至瞬态计算，时间步长设置为0.000 3 s。图4、图5为翼型升阻力系数计算结果与实验值的对比。

可以看出，在小攻角情况下，计算结果与实验结果趋势相一致，故采用该模拟方法对翼型升阻力系数在小攻角范围内进行模拟是合理的。

图4 数值模拟与实验工况下翼型升力系数对比

图5 数值模拟与实验工况下翼型阻力系数对比

2.2 不同攻角下翼型周围质量浓度分析

不同攻角处翼型所对应的质量浓度，如图6所示。分析可知，当质量浓度为30 g/m3，雨滴直径为1 mm时，在11.5°攻角之前，翼型周围质量浓度基本都处于0.070 kg/m3。而在13.5°与15.5°攻角时，翼型周围质量浓度略微下降，处于0.056 kg/m3～0.070 kg/m3。这是因为降雨的入射面与来流方向相垂直，使得翼型周围的质量浓度因为来流的原因，形成雨滴聚集区。在此区域，雨滴的浓度明显高于计算域内其他地方的浓度。且从翼型周围质量浓度分布来看，有大量的雨滴直接接触在翼型的前缘与压力面，雨滴与翼型撞击之后发生破裂、反弹、黏附等一系列的物理现象，造成翼型周围的压力与边界层发生变化，导致其气动性能的损失。

图7为在=0.1、0.5、1、1.5、2 s时不同攻角下翼型表面形成液膜高度变化图。结合图6分析，从形成液膜的整体来看，在翼型的压力面，液膜主要是由前缘形成再逐渐向尾缘发展，当计算进行到0.1 s时，形成液膜的位置主要在翼型前缘附近，大约在0～0.02倍的弦长处，形成液膜高度处于0～0.04 mm，而当计算进行到0.5 s时，压力面已全部形成液膜，高度处于0～0.05 mm。继续进行计算时，压力面液膜高度基本保持一致。在翼型的吸力面，不同攻角下形成液膜波动比较大：当计算进行到0.5 s时，不同攻角下翼型吸力面形成液膜高度基本保持一致，形成液膜位置在翼型吸力面0～0.3倍的弦长处，且液膜高度基本一致，处于0～0.003 mm。当计算进行到0.5 s时，此时，不同攻角下翼型吸力面液膜发生了不同变化，在9.5°攻角下，形成液膜分布于0～0.4倍弦长处，且液膜高度较0.1 s时有明显升高；在13.5°攻角下，此时形成液膜主要有2部分，在翼型前缘0～0.4倍弦长处和尾缘0.6～1.0倍弦长处，并且尾缘处翼型液膜形成高度明显高于在前缘，形成液膜高度分别处于0～0.05 mm和0～0.6 mm；在15.5°攻角下，翼型吸力面形成液膜位置处于0～0.3倍弦长与0.7～1.0倍弦长处，形成液膜高度基本处于0～0.05 mm和0～0.6 mm。当计算进行到1 s时，在9.5°攻角下，翼型吸力面形成液膜高度基本稳定，仅只有在0.8～1.0倍的弦长处形成液膜较低；在13.5°攻角下，在翼型吸力面基本都形成液膜，且液膜高度波动较大；在15.5°攻角下，在翼型前缘形成液膜向尾缘移动且在尾缘处形成液膜逐渐增高期，形成液膜波动较大。当计算进行到1.5 s时，在9.5°、13.5°攻角下，翼型吸力面形成液膜基本稳定，在随后计算中液膜高度也将基本不会发生变化，而在15.5°攻角下，翼型吸力面形成液膜开始逐渐累计并增高，当计算达到2 s时，3种攻角下翼型表面形成液膜高度稳定。产生这一现象的主要原因是在9.5°攻角下，翼型吸力面并无分离泡与附着涡的形成；而当攻角增大到13.5°与15.5°时，翼型吸力面有分离泡与附着的形成，造成在这2个攻角下，一方面，由前缘雨滴撞击翼型表面形成液膜向尾缘流动所造成，另一方面，形成的分离泡与附着涡减缓了形成液膜流动的速度，使得在翼型吸力面大量堆积，造成此2个攻角下吸力面液膜波动更大。

继续分析图7可知，当计算进行到2 s之后，翼型表面液膜达到稳定状态，从翼型表面形成液膜高度来看，在9.5°攻角下，形成液膜由前缘到后缘依次增高，前缘处翼型形成液膜高度大约在0～0.05 mm，而在翼型尾缘处形成液膜高度在0.80 mm，随着攻角的增大，其波动幅度越大。这是因为在翼型的前缘，大量的雨滴撞击到翼型表面时发生破裂、飞溅、反弹等物理现象，并无太多的雨滴黏附于前缘形成液膜。而在翼型的中部，由于雨滴撞击时有倾角，并且形成液膜时将会向后缘移动，导致在中部区域形成液膜高度明显高于前缘，而在尾缘处，由于形成的液膜将会流出翼型，所以此时液膜高度达到最大。从翼型的吸力面来看，在9.5°攻角时，吸力面的液膜并无太大变化，基本都处于0～0.15 mm。而当攻角增大到11.5°时，由于即将要发生分离故在翼型尾缘约0.9 c处液膜厚度开始增高，处于0～0.50 mm之间。当攻角增大到13.5°时，由于在翼型吸力面有分离泡的形成，造成在0.8～0.9 c处的液膜有明显增高，形成一个0～0.55 mm的一个峰值。当攻角在15.5°时，由于在吸力面有附着涡的形成，造成形成液膜的波动更加明显。

2.3 不同雨滴质量浓度对于翼型气动性能的影响

为了研究浓度变化对于翼型气动性能的影响，本文选取了10、20、30 g/m33种不同质量浓度，研究了其气动性能的变化。图6为在9.5°、13.5°、15.5°攻角下翼型周围的浓度变化情况。

由图8分析，由于来流方向与降雨方向垂直的原因，所以在翼型周围将会形成浓度聚集区，造成翼型周围的质量浓度明显高于流场其他区域。在9.5°攻角下：当质量浓度为10 g/m3时，在翼型周围的质量浓度分布在0.035～0.049 kg/m3；当质量浓度增大到20 g/m3时，翼型周围的质量浓度也将增大，为0.049～0.070 kg/m3；当质量浓度为30 g/m3时，翼型周围的质量浓度达到3种质量浓度下最大，为0.070 kg/m3。在13.5°攻角下：当质量浓度为10 g/m3时，在翼型周围的质量浓度分布在0.028～0.042 kg/m3；当质量浓度增大到20 g/m3时，翼型周围的质量浓度也将增大，为0.042～0.063 kg/m3；当质量浓度为30 g/m3时，翼型周围的质量浓度达到三种质量浓度下最大，为0.063～0.070 kg/m3。在15.5°攻角下：当质量浓度为10 g/m3时，在翼型周围的质量浓度分布在0.014～0.035 kg/m3；当质量浓度增大到20 g/m3时，翼型周围的质量浓度也将增大，为0.035～0.042 kg/m3；当质量浓度为30 g/m3时，翼型周围的质量浓度达到3种质量浓度下最大，为0.042～0.070 kg/m3。

图9分别为在9.5°、13.5°、15.5°攻角下翼型表面的液膜高度图，将雨滴直径设置为1 mm，只改变了雨滴的质量浓度，来研究其单一变量下在降雨环境中的翼型气动性能的变化。从左到右依次为翼型表面液膜高度形成图、吸力面液膜高度图、压力面液膜高度图，分析发现，在同一质量浓度下，液膜高度由前缘到后缘逐渐增高，这是因为雨滴在前缘发生碰撞之后产生破裂、飞溅等一系列的物理现象，使得大量破碎之后的雨滴小颗粒散落于流场之中，造成了在前缘形成的液膜较薄。其次因为是翼型本身的形状的原因，NACA0012翼型在中间靠近尾缘的部分，过渡比较平缓，形成的液膜在此流动相对缓慢，形成了一定的堆积，而在尾缘处达到了最大。

从液膜高度分析来看，在9.5°攻角下翼型表面生成液膜高度基本处于0～0.2 mm之间，吸力面的液膜高度处于0～0.05 mm之间，液膜分布相对均匀，而在压力面，相较于吸力面而言，形成的液膜厚度有较大的峰值，最高处有0.2 mm，故压力面与吸力面相比较，压力面波动幅值更大；在13.5°攻角下，翼型表面形成液膜基本处于0～0.60 mm之间，由于在吸力面有分离泡的形成，延缓形成液膜的流速，故在弦长的0.8～0.9倍的弦长处，液膜高度达到一个峰值，为0.60 mm左右，而在翼型的压力面，相较于吸力面而言，波动幅值较小；在15.5°攻角下，翼型表面形成液膜的高度处于0～0.80 mm之间，由于在翼型的吸力面有附着涡的形成，造成在此攻角下，翼型吸力面的波动幅值相比于压力面更大。

图10、图11为在不同攻角下，不同浓度雨滴和清洁空气下翼型升阻力系数变化图。从整体趋势分析来看：随着浓度的增大，翼型的升力系数都比清洁空气小，而且浓度越大，翼型的升力系数变化越明显。3种浓度下，在10 g/m3时，翼型升力系数与清洁空气相比，变化幅度最小，当增大到30 g/m3，此时翼型的升力系数变化幅度最大；与之相反，随着浓度的增大，翼型的阻力系数相比于清洁空气都要偏大，且浓度越大，阻力系数变化越明显。3种浓度下，在10 g/m3时，翼型阻力系数与清洁空气相比，变化幅度最小，当增大到30 g/m3，此时翼型的阻力系数变化幅度最大。

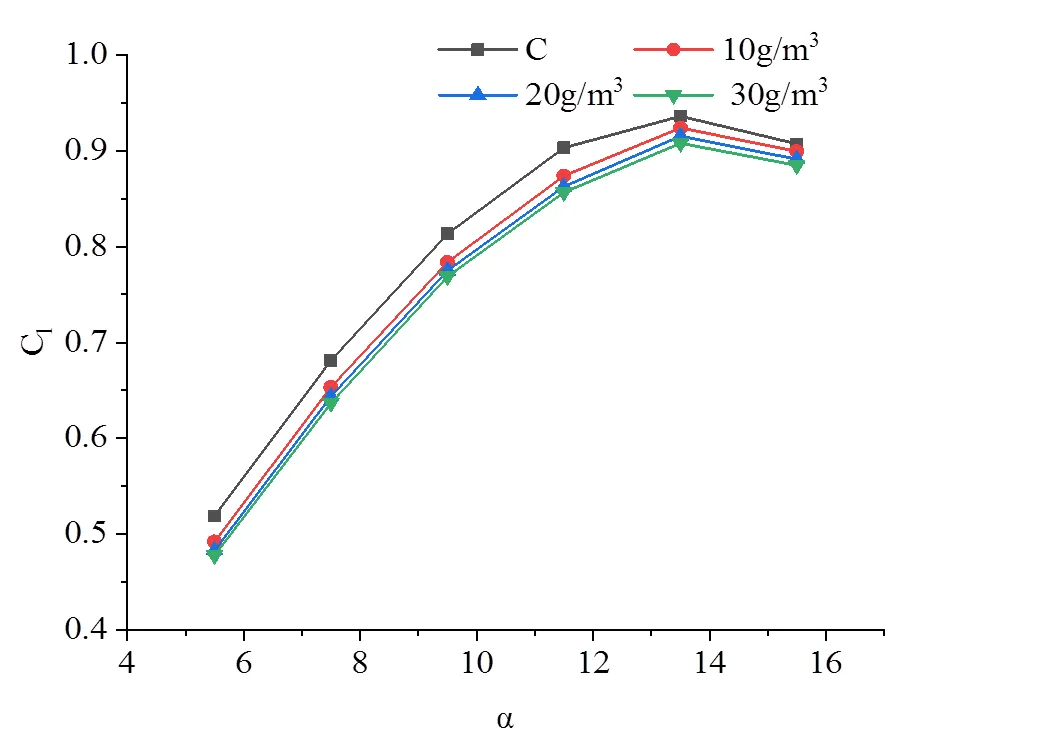
图10 不同浓度下翼型升力系数随攻角变化

图11 不同浓度下翼型阻力系数随攻角变化

3 结论

本文以NACA0012翼型为研究对象，采用标准的-湍流模型进行模拟，得到如下结论：

(1)翼型表面形成液膜厚度影响主要与翼型周围质量浓度相关。

(2)翼型吸力面形成液膜主要是由翼型前缘形成之后向尾缘流动造成的，而在翼型的压力面，形成液膜主要是由雨滴直接与翼型表面碰撞形成。

(3)当雨滴质量浓度增大时，翼型周围质量浓度也随之增加，造成在翼型表面形成液膜厚度也在逐渐增大，对于翼型升阻力系数的影响也随着浓度的增大而增加。

[1] 张瑞民, 曹义华. 降雨条件下翼型的气动特性[J]. 航空动力学报, 2010, 25(9): 2064-2069.

[2] Hsu Y K. An analytic study of a two-phase laminar airfoil in simulated heavy rain [R]. N94-23661, 1993.

[3] Valentine J R, Decker R A. Tracking of raindrops in flow over an airfoil[J]. Journal of Aircraft, 1993, 32(1): 100-105.

[4] ALAN J, BILANIN. Scaling laws for testing airfoils under heavy rainfall[J]. Journal of Aircraft, 1987, 24(1): 31-31.

[5] Yeom G S, Chang K S , Baek S W . Numerical prediction of airfoil characteristics in a transonic droplet-laden air flow[J]. International Journal of Heat and Mass Transfer, 2012, 55(1-3): 453-469.

[6] AIAA. The aerodynamic effect of surface wetting characteristics on a laminar flow airfoil in simulated heavy rain-23rd Aerospace Sciences Meeting (AIAA)[J]. 2000.

[7] Hastings E C, Manuel G S. Scale-model tests of airfoils in simulated heavy rain[J]. Journal of Aircraft, 1985, 22(6): 536-540.

[8] Cai M, Abbasi E, Arastoopour H. Analysis of the Performance of a Wind-Turbine Airfoil under Heavy-Rain Conditions Using a Multiphase Computational Fluid Dynamics Approach[J]. Industrial & Engineering Chemistry Research, 2013, 52(9): 3266-3275.

[9] Valaker E A, Armada S, Wilson S. Droplet Erosion Protection Coatings for Offshore Wind Turbine Blades[J]. Energy Procedia, 2015, 80: 263-275.

[10] Enrique C, Fernando S, Anthony O, et al. On the Material Characterisation of Wind Turbine Blade Coatings: The Effect of Interphase Coating–Laminate Adhesion on Rain Erosion Performance[J]. Materials, 2017, 10(10): 1146.

[11] Launder B E, Spalding DB. Lectures in Mathematical Models of Turbulence[M]. London: Academic Press, 1972.

[12] Markowitz A H. Raindrop Size Distribution Expressions[J]. Journal of Applied Meteorology, 1976, 15(9): 1029-1032.

[13] Ismail M, Yihua C, Wu Z, et al. Numerical Study of Aerodynamic Efficiency of a Wing in Simulated Rain Environment[J]. Journal of Aircraft, 2015, 51(6): 2015-2023.

[14] Hansman R J, Craig A P. Low Reynolds number tests of NACA 64-210, NACA 0012, and Wortmann FX67-K170 airfoils in rain[J]. J Aircr,1987,24 (8): 559-566.

[15] Wu Z, Cao Y . Dynamics of initial drop splashing on a dry smooth surface[J]. Plos One, 2017, 12(5): e0177390.

[16] Ismail M, Yihua C, Wu Z, et al. Numerical Study of Aerodynamic Efficiency of a Wing in Simulated Rain Environment[J]. Journal of Aircraft, 2015, 51(6): 2015-2023.

Effect of Rainfall on Aerodynamic Performance of Wind Turbine Airfoil

WEN Tao, CHEN Chun-lin, WANG Lin-zhu, YANG Yuan-juan

（Gansu Computing Center，Lanzhou 730030，China）

In this paper, NACA 0012 airfoil is taken as the research object, and the effect of raindrops on airfoil aerodynamic performance is studied by using Lagrange discrete phase model. It is found that a liquid film of a certain thickness is formed on the surface of airfoil under rainfall environment. The formation of liquid film affects the smoothness of the airfoil surface and causes transition in advance of boundary layer, which results in the decrease of lift force and the increase of resistance of airfoil. As the calculation time goes on, the liquid film on the airfoil surface is mainly formed by raindrops colliding directly with the airfoil wall on the pressure surface, while on the suction surface, the liquid film is mainly formed by the leading edge of the airfoil and then flows gradually to the trailing edge. When the concentration of raindrops increases, the height of liquid film formed on the airfoil surface fluctuates more, and the influence on its lifting resistance will also increase.

wind turbine; liquid film height; raindrop diameter; aerodynamic performance; mass concentration

10.15916/j.issn1674-3261.2022.01.005

TK83

A

1674-3261(2022)01-0022-09

2021-07-20

甘肃省省属科研院所基础条件建设专项(17JR3TA011)

文洮(1987-)，女，甘肃康乐人，副研究员，硕士。

责任编辑：陈 明