含断齿故障的直齿轮固有特性分析
2022-01-14沙云东栾孝驰
赵 钱 沙云东 栾孝驰,2
(1.沈阳航空航天大学 航空发动机学院 辽宁省航空推进系统先进测试技术重点实验室,沈阳 110136;2.哈尔滨工程大学 动力与能源工程学院,哈尔滨 150001)
在机械系统中,齿轮的工作应力高、精度要求高,有足够的承载能力和可靠性。渐开线圆柱齿轮结构简单、制造方便,是应用最为广泛的一种传动齿轮。但是,在实际工作环境中,齿轮由于长时间工作会出现断齿等问题,从而严重影响齿轮的正常运作。
目前,关于不同齿轮故障在试验和数值仿真分析方面开展了许多研究[1-3]。KUMAR[4]等研究了齿轮不对中对齿轮接触面积的影响。CRABTREE[5]等针对齿轮箱故障,提出了一种在线监测信号分析的方法。孔军廷等[6-7]基于APDL语言开展了含齿根裂纹故障的圆柱斜齿轮的模态分析。冯刚[8]等采用Pro/E软件建立了无裂纹和有裂纹的弧齿锥齿轮三维模型,用有限元法研究了不同位置、不同大小的裂纹对齿轮结构固有特性的影响。张琛良[9]等采用势能法对直齿轮副的径向错位、轴向错位、角度错位3种装配故障进行了齿轮副啮合刚度影响分析。除此之外,关于齿轮的断齿现象也经常发生[10]。王敏[11]等通过解析解方法和有限元仿真分析方法验证了蜗杆发生断齿的位置。高国川[12]等基于有限元仿真方法建立了齿轮箱的动力学模型,分析了正常齿与断齿的箱体振动信号。
目前,相关研究中大多只分析了故障齿轮的振动信号和基本性能参数,关于断齿故障与齿轮固有特性关系的研究很少。因此,本文基于有限元分析方法开展齿轮的固有特性分析,从不同网格划分方式中探寻综合考虑求解效率和求解精度的最优解。针对齿轮的断齿现象,研究断齿程度与齿轮固有特性的关系。
1 有限元模态分析
某直齿圆柱齿轮的参数如表1所示。

表1 齿轮尺寸和材料参数
对齿轮进行模态分析,采取有限元仿真分析的方式,可以更直观地分析齿轮的固有特性。
有限元模态分析主要可以分成以下5步。第1步是建立直齿圆柱齿轮的有限元模型。在UG中建立所要研究的圆柱齿轮模型。建模时,先采用调用表达式的方式建立渐开线,再在通过一系列的阵列、扫描及拉伸等操作后建立实体模型。第2步是输入材料参数。先调用Workbench中的Modal模块进行齿轮模态分析,然后导入步骤1建立好的齿轮模型,并输入表1中齿轮的材料参数,包括弹性模量、密度和泊松比。第3步是对齿轮进行有限元网格划分。划分网格过程中,要同时选取网格划分类型,网格尺寸等参数。第4步是施加边界条件。根据齿轮的实际工作条件,将齿轮的中心孔与轴相连,并对其施加固定约束。第5步是求解与后处理。提取有限元仿真分析结果,由于低阶振型会对齿轮结构的振动产生很大影响,一般情况下提取前5~10阶分析结果。基于计算的分析结果,本次提取前10阶固有频率和振型。
对该圆柱齿轮定义网格划分时尺寸为1 mm,网格类型为六面体,齿轮的模态分析振型图如图1所示,频率值分别为6 580.9 Hz、7 603.4 Hz、12 244.0 Hz、18 898.0 Hz。
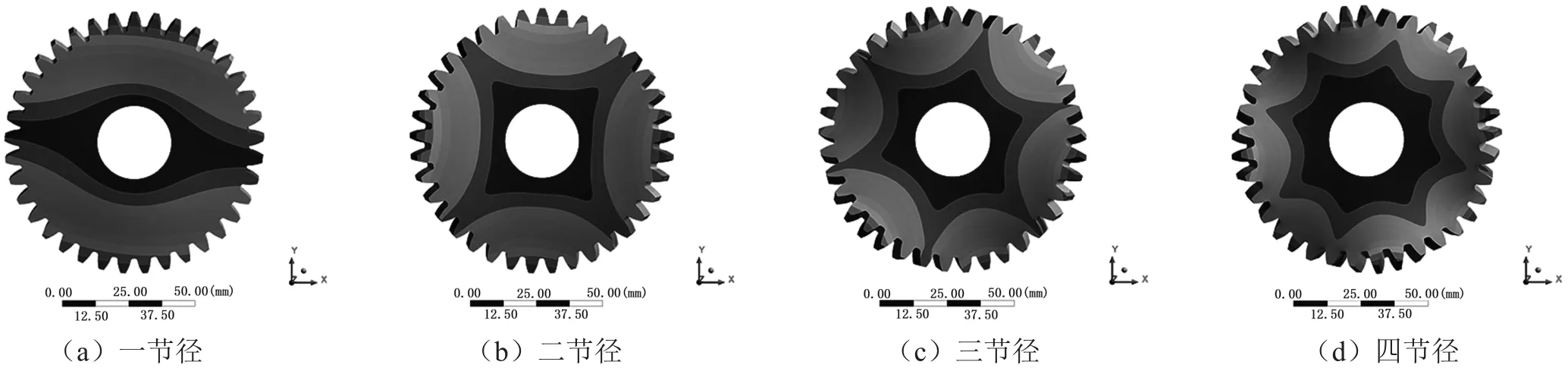
图1 某齿轮的模态分析振型图
2 网格划分方式对齿轮固有特性的影响
与Hypermesh的有限元网格划分前处理功能相比,Workbench不如它的适应性和可定制性,但是Workbench的优点是操作简单。简单的、小规模的模型可以使用Workbench进行网格划分。在齿轮的有限元模态分析中,当网格划分步骤中采取不同网格类型和单元尺寸时,其固有频率值会发生变化。对于直齿圆柱齿轮,可以选用Workbench进行网格划分,其固有频率结果如表2所示。图2和图3分别为采用四面体(2 mm)和六面体(0.4 mm)的网格划分结果时的振型图。

图2 四面体(2 mm)网格划分结果时的振型图
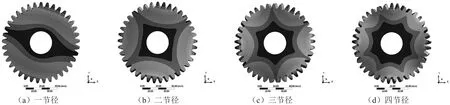
图3 六面体(0.4 mm)网格划分时的齿轮振型图
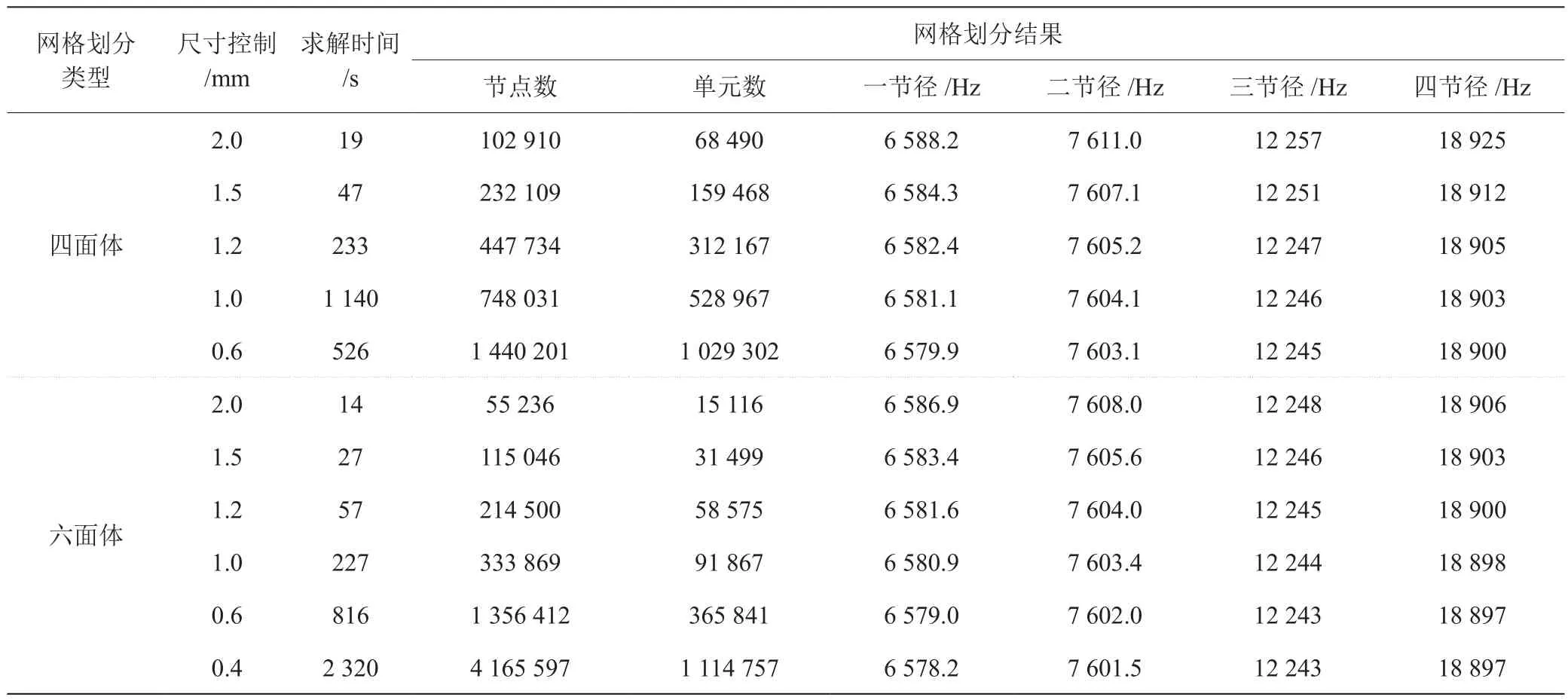
表2 不同网格划分方式时的齿轮固有频率结果
从图2和图3可以看出,该齿轮不同网格划分设置对于模态振型影响不大。对比表2中的数据发现:随着网格单元尺寸的细化,模型的节点数和单元数越来越多,求解时间越来越长;随着网格的细化,各节径下的频率值均减小;当网格细化到一定程度后,频率值变化非常小。因此,合理选择网格尺寸和单元类型有利于在齿轮模态分析时综合计算精度和计算效率。
对于该齿轮模型,综合比较网格数量、求解时间和求解结果,当网格尺寸控制在1 mm时,六面体网格划分方式优于四面体网格划分方式,为理想的网格划分方式。
3 含断齿故障的模态分析
当齿轮存在断齿故障时,需要分析不同程度的断齿对齿轮模态的影响。图4是断齿的定义,图中L为断齿的深度。表3显示了0~2 mm的断齿距离下各相同节径下的模态频率差值。
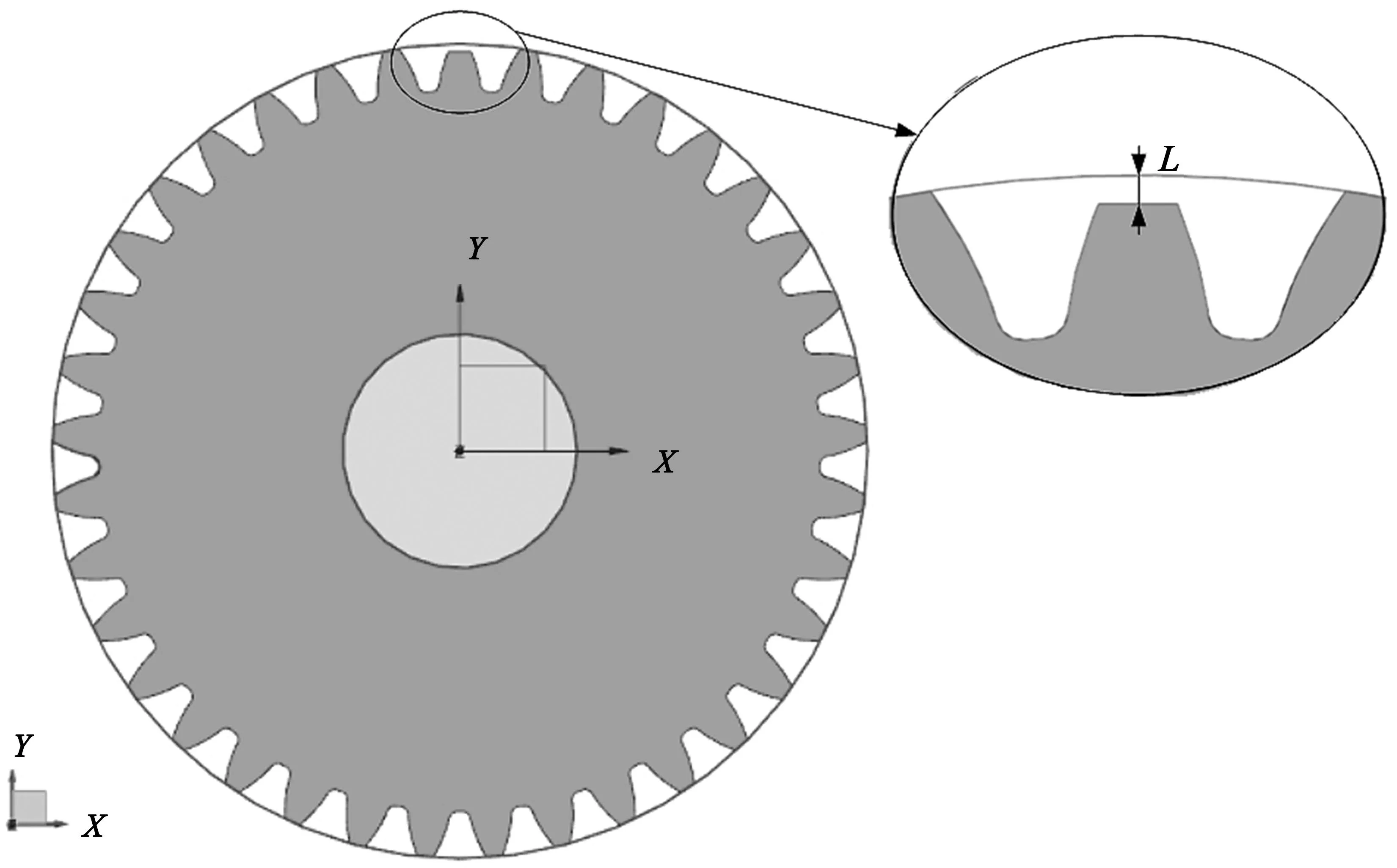
图4 圆柱齿轮的断齿模型

表3 不同断齿程度的圆柱齿轮模态分析频率值
图5是当断齿为1 mm时各阶模态的振型图。从图5可以看出,各阶模态振型没有变化,但是从表3看出随着断齿程度的增加,第1、第4、第7、第9阶次的频率值几乎没有变化,但是第2、第5、第8、第10阶次的频率值不断增加。对比各相同振型的频率差值,如图6所示。从图6可以看出,振型图相同时,断齿程度越大,频率差值越大,且高阶次比低阶次的频率值变化大。

图5 断齿程度为1 mm时的齿轮模态振型
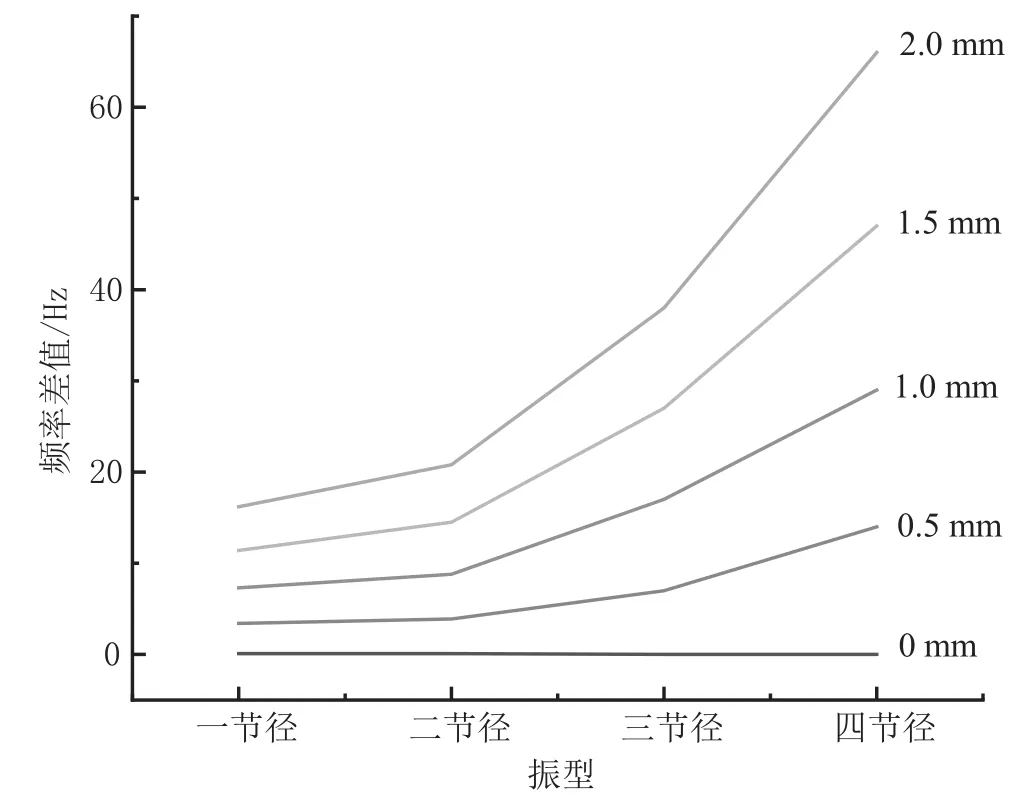
图6 不同断齿模型的相同振型的频率差值
4 结论
通过对直齿圆柱齿轮的模态分析,得到齿轮各阶次的振型和频率值,研究结果如下。
(1)在齿轮有限元模态分析时,采用不同网格尺寸可以得到不同的频率值,综合考虑求解精度和求解效率,有利于获得最优化的模态分析结果。
(2)从含断齿故障的齿轮模态分析得出,随着断齿程度的增加,各模态型第1、第4、第7、第9阶次的频率值几乎没有变化,但是第2、第5、第8、第10阶次的频率值不断增加。在进行齿轮模态试验时,可以通过观察齿轮频率值的变化,判断齿轮的故障情况。
