基于量化风电场限功率的电力系统旋转备用优化研究

蒋成成, 陆建宇, 魏云冰，朱健安，朱成名

(1. 上海工程技术大学 电子电气工程学院，上海 201620； 2. 国家电网有限公司华东分部， 上海 200120)

0 引 言

近年来，以风电为代表的可再生能源发电迅速发展，为缓解环境压力和能源危机做出了巨大贡献。目前，我国的风电装机容量已为世界首位，然而由于风电出力的间歇性、不确定性、不可预测性，大规模的风电并网给电力系统的可靠运行带来了严峻的挑战，所以提供足够的旋转备用容量就显得十分必要[1]。

随着风电并网比例的不断增加，仅仅依靠火电机组提供旋转备用是不够的，并且近年来由于负旋转备用的不足造成的弃风现象也屡见不鲜，造成了巨大的资源浪费和财产损失。所以，如何确定最优的旋转备用成为了学者们重点关注的问题。文献[2]建立了一种以最小发电成本和最小旋转备用本为目标函数的二层规划模型。文献[3]提出了一种基于时间尺度短时修正调度计划的思想。文献[4]完善了电网二次调频备用指标约束，但未能对其进行量化研究。文献[5]提出了一种将不确定性以概率形式综合考量的思想。文献[6]构建了可再生能源的出力不确定模型。但在文献[5-6]的目标函数中对于旋转备用调用的考虑不够充分。文献[7]在SR优化模型的构建中考虑到了机组出力波动。但文献[1-7]在其SR优化的模型的构建中均没有考虑到弃风和失负荷的情况。

文献[8]引入了风险偏好系数，基于加权半方差法建立了模型，但却没有考虑到风险成本。文献[9]基于随机规划的基础上建立了二阶段补偿模型，但在其模型中忽略了风电预测偏差和负荷预测偏差的存在。文献[10]研究了关于自治微网充裕性评估指标的计算模型，但是却认为因风机出力不可控而不能提供旋转备用。据相关研究表明[11-12]，仅仅依靠火电机组来消除风电并网的影响是不现实的，旋转备用需求不能通过增开火电机组来满足。

文献[13]考虑到发电成本、期望停电成本及机组的停运情况，建立了总成本最小的数学模型。文献[14]提出了一种关于微网的旋转备用优化模型，完整地构建了环境成本的多目标函数，但是关于发电成本的建模考虑不全面，约束条件也过于理想。文献[15]提出了一种风火联合运行的数学模型，但却过于轻视机组运行的可靠性。文献[16]将弃风、切负荷分别作为一种特殊的负、正旋转备用。文献[17-18]详细讨论了机组组合的出力优化方案。但以上文献中所构建的风电模型均以最大风能利用模式建立。

针对上述研究的不足，考虑将风电场限功率运行，并将风电场的限功率量作为一种特殊的负旋转备用，相应地把可中断负荷作为正旋转备用应用到发电调度模型中，以包含发电成本、启停成本、旋转备用调用成本、可中断容量成本、限风成本、约束违反成本的总运行费用最小，建立了兼顾可靠性与经济型的SR优化模型。最后，以不同的限功率值与负荷需求为依据划分出数个场景，通过量化分析验证所提模型的准确性与优越性。

1 系统不确定性模型

1.1 负荷模型

负荷模型如下所示：

PL=PLP+eL

(1)

式中PL为系统实际负荷；PLP为预测负荷；eL为负荷预测偏差。短期负荷预测中的负荷预测偏差eL服从均值为0、标准差为σL的正态分布。又有：

σL=k%PLP

(2)

其中k可以取1～100之间的任意值[16]。

1.2 风电出力模型

1.2.1 风电不确定模型

PW=PWP+eW

(3)

式中PW为风电实际功率；PWP为风电预测功率；eW为风电预测偏差。文中认为eW服从均值为0，标准差为σW的正态分布，又有[16]：

σW=0.2PWP+0.02PW,cap

(4)

式中PW,cap为风电场总装机容量。

1.2.2 限功率运行的含义

在风电场限功率量Pc引入之前有：

PW=PL-Pd

(5)

PW=PWmax

(6)

Pd=PL-PWmax

(7)

波动状态下有：

ΔPd=ΔPL-ΔPW

(8)

风电场限功率运行,即：

PWmax-Pc=PL-Pd

(9)

由式(8)、式(9)可知在限功率波动状态下有：

(10)

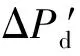
1.3 系统净负荷模型

系统净负荷在传统意义上的定义为系统负荷减去风电出力值[19]。由于引入了Pc的概念，所以系统净负荷还应在传统定义的基础之上考虑到Pc,计及负荷预测偏差与风电预测偏差的系统净负荷不确定模型如式(11)所示：

Pn=(PLP+eL)-(PWP+eW-Pc)

(11)

式中Pn为系统净负荷。

1.4 发电机停运模型

在发电机故障停运模型中考虑到了机组强迫停运概率[20]。假设机组只存在两种状态：故障状态及正常运行状态，当第i台机组处于正常运行状态时，将其记为ui=1，处于故障停运状态时，记为ui=0，故障率设为λ，正常运行概率为1-λ，如表1所示。

表1 机组故障停运模型Tab.1 Unit failure shutdown model

2 风电场限功率运行对电网二次调频的影响

2.1 对旋转备用的影响

从公式(11)可以看出，当引入限风功率值Pc时，风电场的实际出力变小，进而使得净负荷Pn增大，从某种程度上而言增加了系统对风电的消纳能力。因此，Pc的设置可以在很大程度上缓解系统负旋转备用的压力。考虑到Pc的设置可能会损失一部分经济效益，引入Pc的价值与取值权衡将在后面算例中用数据进行更为详细地说明。

2.2 对二次调频速度的影响

二次调频速度定义为单位时间内机组出力的变化量，需满足：

(12)

其中VS为二次调频速度；Ts为二次调频时间。当风电场限功率运行时，二次调频速度为：

(13)

式中Vi为第i台同步发电机的调频速度；NG为同步发电机数量。

2.3 对风电装机规模的影响

风电总装机容量为Pw,cap，则有：

ew∈[0-φσw, 0+φσw]Pw,cap

(14)

式中φ为风功率波动系数，其值可以根据实际情况人为选取。

根据系统对调频速度的要求，可知：

(0+φσW)PW,cap≤Vs

(15)

(16)

在风电限功率运行状态下，有：

(17)

式中P′W,cap为风电场限功率运行状态下的风电总装机容量。由上节可知Vs′>Vs，对比式(16)与式(17)可以看出Pc的引入使得电网二次调频速度增加，进而使得风电场装机容量的上限增大，即引入限功率量Pc会增大风电场的装机规模。

3 机组组合模型

3.1 目标函数

发电成本、启停成本、旋转备用调用成本、可中断容量成本、限风成本、约束违反成本之和最小的目标函数如式(18)～式(20)所示：

(18)

(19)

Ci,t(Pi,t)=aiPi,t2+biPi,t+ci

(20)

式(18)～式(20)中，g为约束违反量；J为总运行费用；Ci,t(Pi,t)为发电成本函数；Pi,t为机组i在t时段的有功出力；ai、bi、ci分别为发电成本的各项系数；ui,t为启停状态；Si,t启动费用；αi为第i台机组上调单位旋转备用的报价；Ru,i,t为第i台机组、t时段内预留的正SR容量；γi为第i台机组签约的可中断负荷容量报价；RL,i,t为第i台机组t时段的可中断容量；μ为限功率损失系数；Pc,j为第j个风电场的减载量；βi为约束违反报价。

3.2 约束条件

(1)系统功率平衡约束。

Pd=(PLP+eL)-(PWP+eW-Pc)

(21)

式中Pd为传统机组出力。

(2)火电机组出力约束。

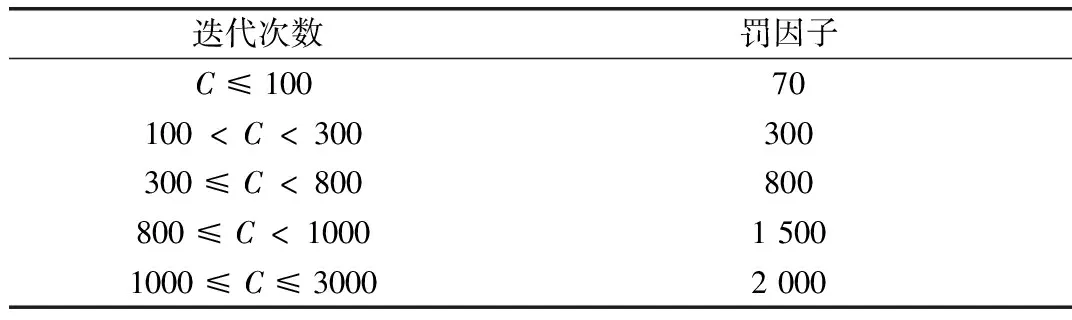
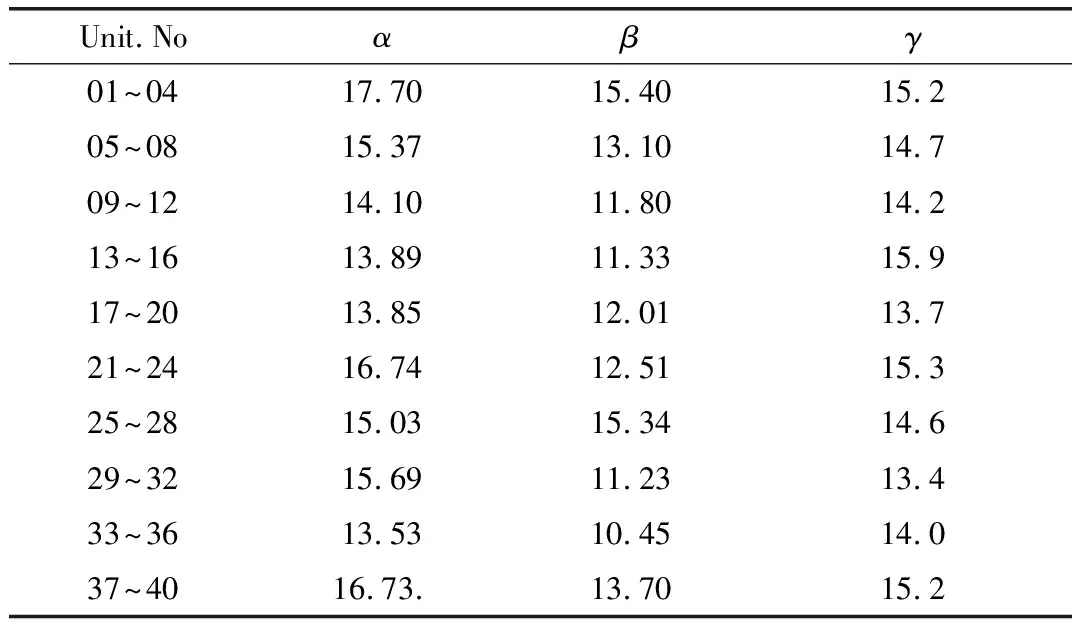
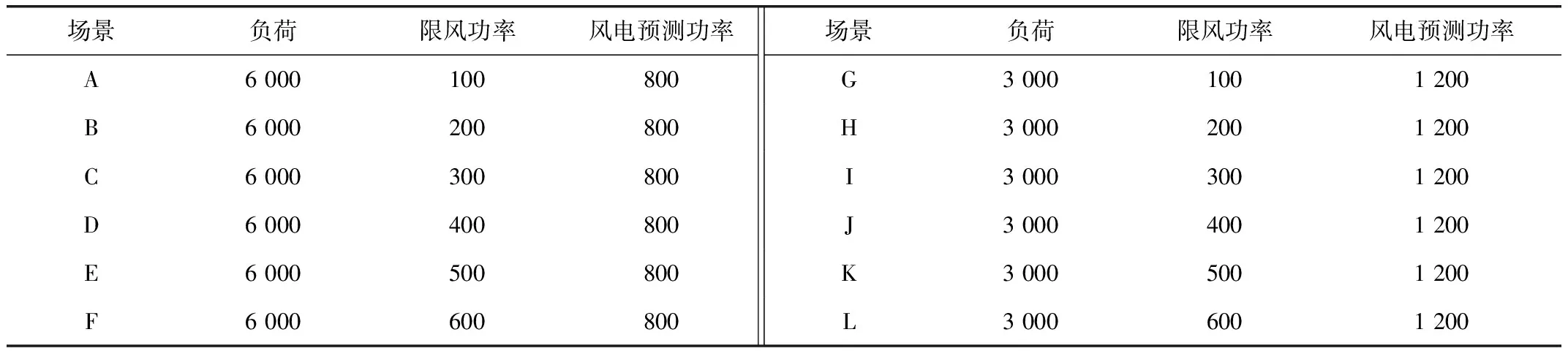
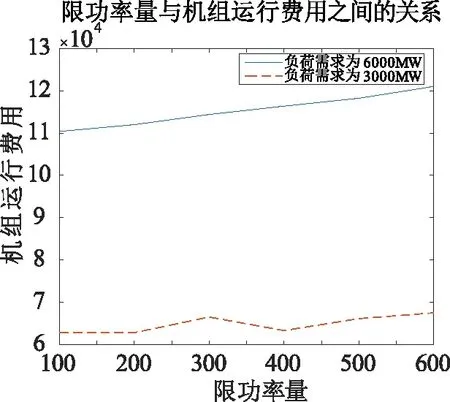
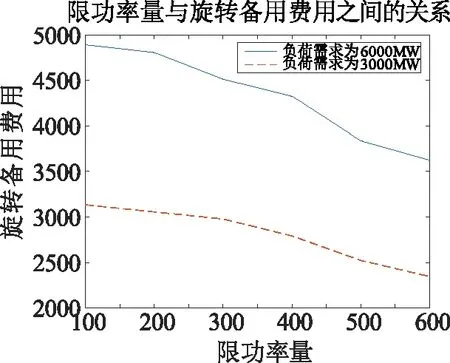
Pimin

(22)

式中Pimin为第i台机组的最小出力；Pimax为第i台机组的最大出力。

(3)二次调频速度约束。

二次调频速度必须满足式(23)才能保证系统的调频能力，详见2.2节。

(23)

(4)风电场最大装机容量约束。

风电场最大装机容量与负荷预测偏差、风电预测偏差、风电场限功率量等指标均有关，详见2.3节。

(24)

(5)弃风概率约束。

将风电场限功率部分作为特殊的负旋转备用，其存在降低了弃风的可能性，但这并不意味着弃风现象就不会发生，因此，合理的做法是确保系统的弃风概率小于预先设定的置信度。

Pr{A}≤βW

(25)

事件A表示弃风，βW为可接受的置信度。其中Pr{A}可由蒙特卡洛抽样获得。即统计因系统负旋转备用不足而产生的弃风事件占总事件的比例。

(6)切负荷概率约束。

这里的切负荷约束指的是针对已签约可中断负荷的约束，将已签约的可中断负荷作为特殊的正旋转备用，当系统有较多的正旋转备用需求时，将可中断负荷切除,可以弥补系统传统正旋转备用的不足，但是大量切负荷是不现实的。因此，科学的处理方法是确保系统的切负荷概率小于预先设定的置信度。

Pr{B}≤βL

(26)

事件B表示切负荷，βL为可接受的置信度。其中Pr{B}可由蒙特卡洛抽样获得。即统计因系统正旋转备用不足而产生的切负荷事件占总事件的比例。

4 模型求解

采用粒子群算法(PSO)来求解，通过粒子的迭代来优化候选方案。

4.1 基于变异策略的PSO算法介绍

PSO算法初始为一群随机的粒子，通过多次迭代找到最优解[21]。粒子可以通过自身找到的最优解(个体极值)来更新自己，也可以通过整个种群找到的最优解(全局极值)来更新自己[22]。

假设i个粒子组成一个种群，则通过个体极值与全局极值的结合来更新粒子的速度和位置，第i个粒子的速度和位置分别为：

Vi=WVi+C1R1(Ebest-Pli)+C2R2(Gbest-Pli)

(27)

Pli=Pli+Vi

(28)

式中W为惯性权重；C1、C2为学习因子；R1、R2分别为[0,1]区间上的随机数；Ebest为个体极值；Gbest为全局极值。

PSO算法可能由于受限于局部最优而找不到真正的最优解，为了解决粒子群的局部受限问题，将基础的PSO算法与变异策略相结合，称之为MPSO[23]。通过设定粒子的变异概率，从而提高该算法对解空间开发的能力，降低了结果陷入局部最优的概率。在迭代的前半部分设定较大的变异概率以便跳出局部最优，迭代的后半部分通过适当地减小变异概率来加强粒子的局部寻优能力。

4.2 步骤

具体算法步骤如下：

(1)输入机组参数、能耗方程系数等原始数据；

(2)初始化粒子速度、位置、机组出力；

(3)计算适应值并更新粒子位置，记录最优目标值；

(4)附加粒子速度约束、机组出力约束等约束条件；

(5)设定分阶段的变异概率；

(6)依据粒子当前迭代次数，设置不同等级的罚因子，解出机组运行成本及旋转备用成本；

(7)对风功率和系统负荷水平进行抽样，根据各机组的出力组合求解出最小停电费用、切负荷概率、弃风概率。

5 算例

本算例系统由40台火电机组组成，火电机组总装机容量为6 648 MW，另有装机容量为1 500 MW的大型风电场接入火电系统。

MPSO参数设置如下：粒子数为80个，迭代次数为30 000次，维数设置为40，初始惯性权重为1，学习因子C1与C2均设置为2，粒子最大速度为0.4。

初始出力：

Pinitial=R×(Pmax-Pmin)+Pmin

(29)

式中R为[0,1]区间的的随机数。

动态惯性权重W应随着迭代次数的增加而减小，即：

(30)

式中n为迭代次数。

粒子初始速度为：

Vinitial=0.02R′-0.1

(31)

式中R′为[0，1]之间的随机数，粒子初始速度控制在-0.01～0.01之间。

采用递增的罚因子，罚因子分为几个等级，随迭代次数改变。

如表2所示，罚因子的最小值设置为70，最大值设置为2 000。分别在迭代次数为100、300、800、1 000时进行不同等级罚因子的替换。算例参数补充见表3。

补充参数中的α、β、γ分别为上调容量报价、约束成本违反报价、可中断负荷容量报价。算例的不同场景设置主要考虑负荷需求、限风功率、风电预测功率三部分内容。

表2 罚因子设置Tab.2 Penalty factor setting

表3 发电机组补充参数Tab.3 Additional parameters of generator set

考虑到火电机组出力限制和风电机组的稳定出力范围，结合实际情况，设置大小两个负荷需求与风电预测值，将大的负荷值设置为6 000 MW，对应的风电预测功率为800 MW；小的负荷值设置3 000 MW，对应的风电预测功率设置1 200 MW。文献[24]默认风电降载10%，为了讨论限功率运行的意义，对风电降载数值进行了多等级的量化分析，将Pc值在100 MW～600 MW之间等差设置来进行仿真。算例场景设置参数详见表4。

考虑到火电机组的启停成本较大，所以在此次仿真中将全部机组启动。随着机组编号的增大，机组在满负荷下的平均耗费也是逐渐增大的，所以在各个机组组合方案的选择中，优先选用编号靠前的机组满负荷运行，并将编号靠后的机组优先以最小功率运行，可以产生更小的运行费用。表5为各场景的计算结果。

分析表5数据可知，在大的负荷需求下，应当适度增加风电场的限功率量。如负荷需求在6 000 MW的系列场景下，场景A、场景B、场景D都是较好的选择，这些场景中失负荷概率均相对较低，但场景D的经济性和可靠性都要优于场景B。场景A与场景D对比来看，场景A的经济性好一些而场景D更为可靠。如何得到综合经济性与可靠性的最优解，还需结合实际考虑；在小的负荷需求下则应尽可能增大风电场的限功率量，此时增大限功率量能明显地提高系统的运行可靠性，限功率量越大，弃风概率越低。如负荷需求在3 000 MW的系列场景下，场景L的失负荷概率与弃风概率均为0，这说明场景L下的可靠性已经达到了非常高的程度，此时场景L相对场景G的机组运行费用不到一成的增加就显得不太重要了，也就是说限功率量为600 MW时可以取到综合经济性与可靠性的最优解。另因其弃风概率与失负荷概率均已为0，也就没有必要继续增加限功率量了。

表4 算例场景设置Tab.4 Example scenario settings MW

表5 场景计算结果Tab.5 Calculation result of each scenario

为了更好地分析限功率量与系统运行的经济性及可靠性之间的关系，将表5中的机组运行费用与旋转备用费用绘制成曲线图，如图1、图2所示。

图1 限功率量与机组运行费用之间的关系Fig.1 Relationship between the limited power and the operating cost of the unit

图2 限功率量与旋转备用费用之间的关系Fig.2 Relationship between limited power and SR cost

从图1中可以看出，在大的负荷需求下选择较小的限功率量可以产生更小的运行费用，但是在小的负荷需求下，不同限功率量产生的机组运行费用基本相同。具体来看，机组的运行费用随着限功率量的增加基本上是逐渐增加的，其中在负荷需求为6 000 MW的情况下，限功率量与机组的运行费用呈现出完全正相关的趋势。如果单从经济方面来考虑，在大的负荷需求下选择较小的限功率量可以产生更小的运行费用。在负荷需求为3 000 MW的情况下，虽然运行费用在整体上随着限功率量的增加是呈现上升趋势的，但是这个趋势并不明显，甚至限功率量为400 MW所对应的运行费用还要明显小于限功率量为300 MW的运行费用，而限功率量为300MW所对应的运行费用基本和600 MW时相当，这说明在小的负荷需求下确定限功率量的数值时，机组运行费用所占的权重可能要小一些。

从图2中可以看出，随着限功率量的增大，其旋转备用费用均呈现出明显的降低趋势。结合图1和图2可以看出，在负荷需求较小的情况下可以尽可能地增大风电场限功率量，这样既可以减小机组的总运行费用，又能提高系统整体的可靠性。但在大的负荷需求下，随着限功率量的增加，机组的总运行费用增加，但旋转备用费用却降低了，机组可靠性也相应地提高。因此，大的负荷需求下限功率量为何值时才能达到综合经济性和可靠性的最优解，还应取决于风电场是否有意愿牺牲一定的经济来换取更高的可靠性。

6 结束语

为了研究风电场限功率状态下的SR优化问题，建立了一种更为可靠也不失经济的旋转备用模型。目标函数修正为发电成本、旋转备用成本、风电场限功率成本、失负荷成本、约束违反成本的总和最小，充分考虑到了风电并网的各种情况，对现实中的电力系统运行具备一定的指导价值。基于MATLAB编程，使用基于变异策略的粒子群算法结合蒙特卡洛模拟进行求解。依据不同负荷需求、不同限功率量与风电预测值选取了一系列场景，分别解出系列场景中各项经济性指标与可靠性指标，并对各项数值进行分析。结果表明：

(1)风电场限功率运行可以明显地降低系统的旋转备用需求,显著提高系统的可靠性；

(2)将风电限功率进行量化研究具有显著地现实意义，通过定量分析不同负荷需求下各等级限功率值的各项经济性与可靠性指标，可以直观地对比出机组的各项费用与弃风、失负荷概率的数值及走势，风电场可根据自身的经济情况与负荷需求选择合适的限功率量；

(3)各种负荷需求下，一定范围内限风功率值的增加都会带来一系列的可靠性收益。