全变差曲波变换在医学影像图像去噪中的应用

陈 军

( 甘肃中医药大学(定西校区) 医学教学部, 甘肃 定西 743000 )

0 引言

医学影像图像在获取过程中不可避免地会受到噪声污染，因而抑制图像获取过程中的噪声对提高图像的边缘、纹理和细节的清晰度以及消除截断伪影具有重要意义.近年来，一些学者运用小波理论探讨了提高图像的低频近似部分信息和高频细节部分信息的方法，但这些方法存在“过扼杀”系数、边缘信息表达不足及周边噪声无法抑制等问题[1-3].为了克服上述问题，一些学者提出了多尺度几何分析方法.例如： 2005年， E.J.Candès等[4-5]提出了一种脊波变换方法，该方法能较好地提取图像特征,且抑噪能力优于小波变换方法，但其描述曲线特征的能力较差.2007年， Marjan等[6]将二元曲波变换应用于图像噪声抑制，该方法虽能有效地去除噪声，但由于其过多地抑制了反映图像不同方向的细节、纹理等高频系数，因而易产生伪影.2009年， B.Amir等[7]提出了全变差去噪声和去模糊算法，该方法虽然能够克服图像滤波时出现的边缘模糊和位移等问题，但存在计算复杂和边缘信息不稳定的缺点.2014年，胡辽林等[8]提出了一种改进的各向异性全变差去噪算法，该方法对图像中的低频噪声具有较好的去除效果,但对高频噪声的去除效果并不理想.2020年，陆焱等[9]提出了一种采用曲波变换对高频细节图像去噪的算法，该方法可增强含噪图像细节的清晰度，但对图像的概貌和视觉识别感知较差.2021年，何明[10]提出了一种基于L1范数和自适应全变差的去噪算法，该方法能有效地抑制图像的椒盐噪声，但对高斯噪声的去噪效果较差，易产生阶梯效应.基于上述去噪研究中出现的截断伪影和边缘模糊、细节不清晰的问题，本文提出了一种全变差曲波变换算法，并通过仿真实验验证了该算法的有效性.

1 全变差曲波变换算法分析

1.1 含噪医学影像图像模型

本文建立的含噪医学影像图像模型为：

μ0(x,y)=μ(x,y)+N(x,y)，

x=0,1,…,m-1;y=0,1,…,n-1.(1)

其中：μ(x,y)是原始医学影像图像；N(x,y)是均值为0、标准差为σ的高斯白噪声，服从N(0,σ2)分布；m和n分别为图像在x方向和y方向上的像素数；μ0(x,y)为加入噪声后的医学影像图像.

1.2 曲波变换去噪算法分析

曲波变换方法是通过建立一组具有各向异性的基来求解空域图像在这组基底上的相关值[11].曲波变换去噪的方法是：首先将含噪图像分解成不同尺度的子带，并通过Plancherel运算得到每个子带所对应的曲波变换系数；然后用硬阈值法对所得到的曲波变换系数进行处理(放弃较小的变换系数，保留较大的变换系数)，以此实现滤除图像中的噪声和保留图像的边缘特性.曲波变换去噪的硬阈值表达式[12]为：

(2)

式(2)中C(i,h)为尺度i和方向h上的曲波系数，Ti为不同尺度所对应的阈值，C0(i,h)为硬阈值处理去噪之后的曲波变换系数.阈值Ti的选取表达式为:

Ti=ki·σ·σi，

(3)

其中σ为噪声标准差，σi为子带变换后所对应的噪声标准差，ki为每一子带所对应的自适应常数.本方法中采用具有强适应性的蒙特卡洛算法估计噪声标准差.

1.3 全变差去噪算法分析

全变差方法是建立在数学模型基础上的一种关于能量泛函求极值的去噪方法[13].全变差去噪的方法是：首先用变分方法导出偏微分方程，然后再通过对图像反复迭代求解出方程的最优解[14].由于无噪图像的全变差小于含噪图像的全变差，故全变差去噪可表示为：

(4)

式(4)中，Ω为图像面积， |∇μ|为图像μ的梯度模.由最小化图像的全变差可得到以下两个约束条件：

(5)

由于含噪声图像的全变差显著大于无噪声的全变差，所以采用最小化全变差可以消除图像中的噪声信号.因此，本文引入拉格朗日乘数法，以便于将约束条件(5)变换为无约束的极值表达式.变换后得到的图像去噪的全变差为：

式(6)中:第1项为μ的全变差范数，它的作用是减少震荡和平滑图像；第2项为逼近项，其决定原始图像μ和含噪图像μ0的差异；λ为拉格朗日乘子，λ>0.λ值越大，μ越逼近μ0， 即图像的细节被平滑得越弱，去噪效果越差；λ值越小，μ越远离μ0， 即图像的细节和噪声被平滑得越强，去噪效果越好.因此，图像去噪的全变差模型[15]可等价为：

式(7)中， 1/|∇μ|为扩散系数，初始条件为μ=μ0.采用梯度下降法迭代求解出方程的最优解，最终获得去噪后的图像.由式(7)可知，扩散只发生在与梯度正交的方向上，因此全变差模型可有效去除医学影像图像中的噪声和保持图像的边缘特征，但其在平滑区域会产生阶梯效应.

2 全变差曲波变换去噪的流程与实验仿真

2.1 全变差曲波变换去噪的流程

在医学影像图像中，由于图像的基本信息主要由低频系数体现，图像的边缘和细节信息主要由高频系数体现，因此需采用不同算法来处理图像的高、低频信息.因加权平均算法在处理图像低频成分方面具有平滑去噪及有效消除截断伪影的优点，因此本文采用加权平均方法处理图像的伪影.令两幅源医学影像图像分别为X和Y， 最终的合成医学影像图像为Z， 则图像平滑去噪及消除截断伪影的加权平均法可表示为：

C(Z,p)=kC(X,p)+(1-k)C(Y,p)，(8)

其中k为加权系数(根据表1数据，本文取k=0.5)，p=(x,y)表示曲波系数的空间位置.

表1 k参数与C(Z,p)的对应值

由于利用绝对值取大算法处理图像高频成分时能充分提取曲波变换阈值去噪后的图像边缘和纹理信息，因此本文采用绝对值取大方法处理图像的纹理细节.绝对值取大算法为：

C(Z,p)=

全变差曲波变换去噪算法的流程图如图1所示.

图1 全变差曲波变换去噪算法的流程图

2.2 实验仿真结果与分析

为检验全变差曲波变换方法的有效性，利用Matlab平台[16]将本文方法和单一的曲波、全变差方法对医学影像图像的去噪效果进行实验对比.实验用图像来源于医学图像数据集(https://www.kaggle.com/felipekitamura/head - ct - hemorrhage)，图像大小为512像素×512像素，如图2所示(图2(a)为原始图像，图2(b)为加入标准差σ=25的高斯白噪声的图像).图3中的(a)、(b)、(c)图像分别为对图2(b)进行曲波变换、全变差、全变差曲波变换的结果.

图2 原始图像(a)和加噪(σ=25)的医学影像图像(b)

图3 曲波变换(a)、全变差(b)、全变差曲波变换(c)算法的去噪效果

由图3可以看出，3种算法虽然都能够有效去除噪声，但存在差异.其中：曲波变换去噪算法(图3(a))可有效滤除噪声和保持医学影像图像的边缘、纹理等细节信息，但在图像边缘处产生了明显的由硬阈值法造成的截断伪影，进而使得图像产生了一些原本不存在的印迹；全变差去噪算法(图3(b))虽然保持边缘的效果较好，但其丢失了较多纹理等细节信息，使得纹理细节变得模糊，并出现明显的块状效应；全变差曲波变换去噪算法(图3(c))在有效去除噪声的同时较好地保持了图像边缘及纹理等细节信息，即能有效克服曲波变换去噪算法产生的截断伪影现象以及全变差去噪算法出现的细节丢失和块状效应问题.由以上可以看出，本文提出的算法在保留图像的边缘、纹理、细节等信息方面以及在消除截断伪影方面显著优于曲波变换去噪算法和全变差去噪算法.

表2为曲波变换、全变差、全变差曲波变换算法去噪时的峰值信噪比.由表2可知，在不同标准差的噪声下，全变差曲波变换算法的峰值信噪比均高于曲波变换去噪算法和全变差去噪算法，由此进一步表明全变差曲波变换算法的去噪效果优于曲波变换去噪算法和全变差去噪算法.

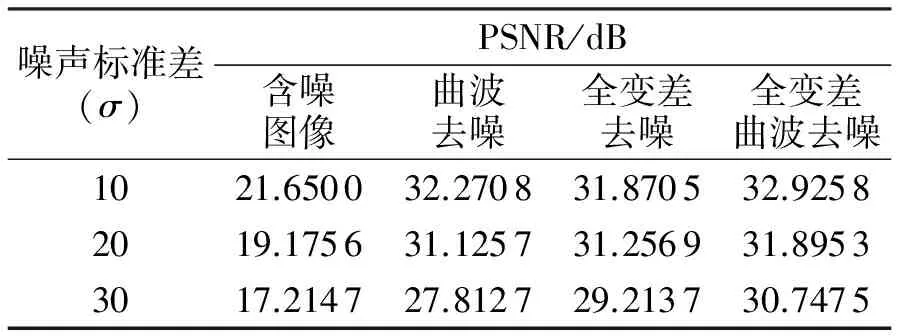
表2 曲波变换、全变差、全变差曲波变换算法去噪时的峰值信噪比

3 结语

研究表明，本文提出的全变差曲波变换算法具有较好的去噪声性能，能够很好地保持图像的边缘、纹理和细节等信息，同时可削除截断伪影；因此，本文提出的算法对医学影像图像的去噪具有很好的应用价值.在今后的研究中我们将对算法的鲁棒性做进一步研究.