多形态拟合水下潜器欠驱动运动控制与目标跟踪

辛光红 陈晓虎 韩建芳

(三亚学院，海南三亚 572000)

1 概述

多形态拟合水下潜器（以下简称ARG）因为系统中只有质量块位移和航向角作为控制输入，在空间运动控制中是一个典型的欠驱动系统。同时,在目标跟踪控制问题中即使没有姿态的约束,虽然也有三个位置偏差需要控制,但仍然多于控制输入的数量。欠驱动系统是指空间维数低于构形空间维数的控制系统,或指令输入低于控制系统控制自由度的控制系统。欠驱动控制水下潜器, 是一个输入维数远小于控制系统自由度的零点五自主水下机器人[1]。为了完成精确的水下任务，具有六自由度和全自由度运动的自主水下航行器通常需要配备多个推进器。按照深水下潜器的驱动特点,把水下航行体分成欠驱动、过驱动和全驱动二种型式[4-5]。本文在进行目标跟踪控制时，根据执行机构的特点，合理地描述潜器与目标点之间的位置关系。然后，再受力分析得到数学关系，构造出实现目标跟踪的性能指标函数项。如图1 所示，输入- 输出推力反馈图反映了六自由度水下航行器控制系统与输出系统之间的关系。

图1 推力反馈图

2 欠驱动水平运动控制

对欠驱动水下机器人三自由度水平运动方程与轨道方程的简化,并设计了自动诊定与稳定控制器。通过全局微分与同胚坐标转换, 把欠驱动水下机器人的数学模型转换成级联非线性系统[2]。证实了原网络系统的诊断为问题,可简化成级联子系统的诊断为问题。通过对状态反馈控制器的研究,对该控制器的自诊定控律进行了数学描述,并证实了该控律的收敛性,而仿真试验则证实了该控制器的自诊定性能[3]。

水下机器人船体惯性坐标系与动力参考坐标系转换的运动学方程为:

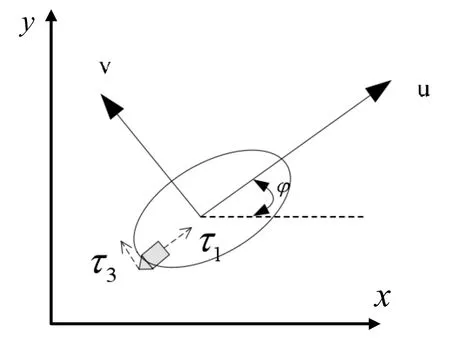
图2 ARG 平面运动坐标系

3 垂直运动控制及跟踪控制

本文运动轨迹控制均假设为与时间无相关曲线参数进行描述。在欠驱动控制下，ARG 从任意初始位置以所需速度按预设参数曲线运动。收水下潜器能量消耗约束，大多数水下潜器设计为回转体结构，仅保留纵向速度及俯仰角速度可控，水下潜实现器垂向运动及路径跟踪控制是设计的难点。垂直面自适应性模糊反步滑模路径跟踪控制器设计原理如下：

3.1 设计速度自适应模糊反步滑模控制器

纵向速度控制器为：

为了实现水下潜器跟踪误差收敛，对于H1 取值令| Q1| >0，当Q1= h1时满足纵向速度满足收敛误差。

3.2 设计俯仰角自适应的模糊反步滑模控制器

设计俯仰角自适应模糊反步滑模控制器设计如（7）、（8）式子所示：

通过上述（1）（2）两步，实现速度误差和航向角误差跟踪收敛。

4 仿真分析

为了验证所设计的垂向运动及跟踪控制器的有效性，利用MATLAB/SIMULINK 对多形态拟合水下潜器进行了仿真。以标称模型用作被控制对象。

假设水下潜器在水平和垂直三维坐标下分别受到5N/m 的外部干扰，以表1 所示参数进行直线和正弦路径跟踪。直线路径的参数方程为：

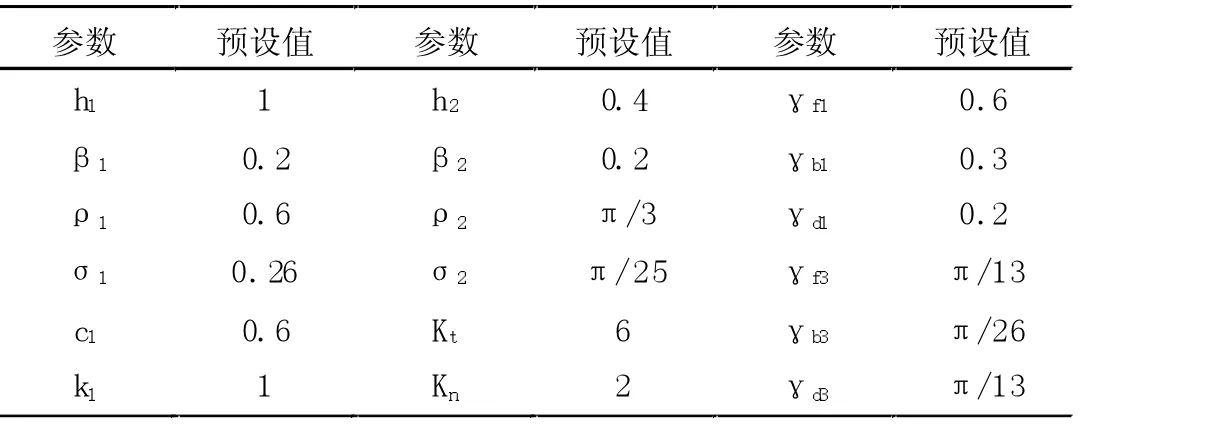
表1 垂向跟踪预设参数

正弦路径跟踪曲线和纵向速度控制曲线分别如图5、6 所示。

通过仿真验证图3～6 表明，在ARG 仿真模型在受外界干扰的情况下，所设计的垂向路径控制器能够快速收敛水下航行体的纵向速度至期望值。实现了水下潜器欠驱动垂向运动路径跟踪，设计的控制器路径跟踪误差较快的实现了归零收敛。在控制性能方面，直线和正弦曲线跟踪过程中，潜器器的最大俯仰角分别为23.7 度和19.2 度，基本满足俯仰调节阈值要求。除上述追踪轨道外,能够选择同样的限制技术参数,体现了控制器优秀的自动适应能力与鲁棒性。

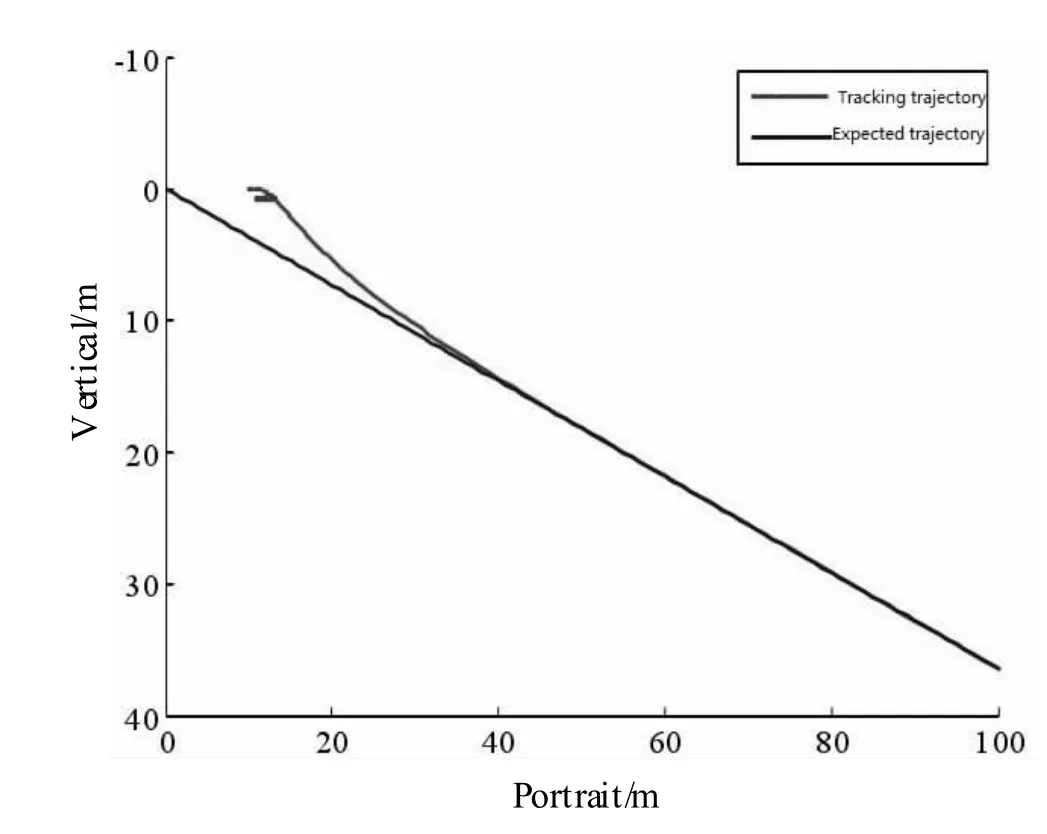
图3 直线路径跟踪曲线

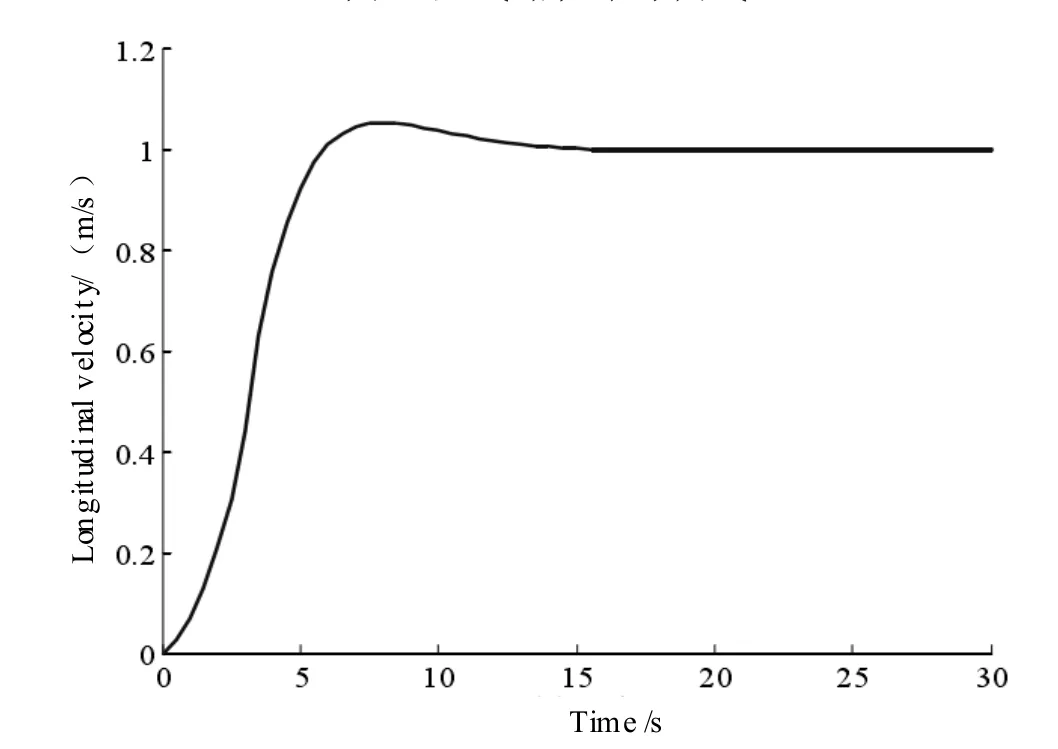
图4 直线纵向速度控制曲线

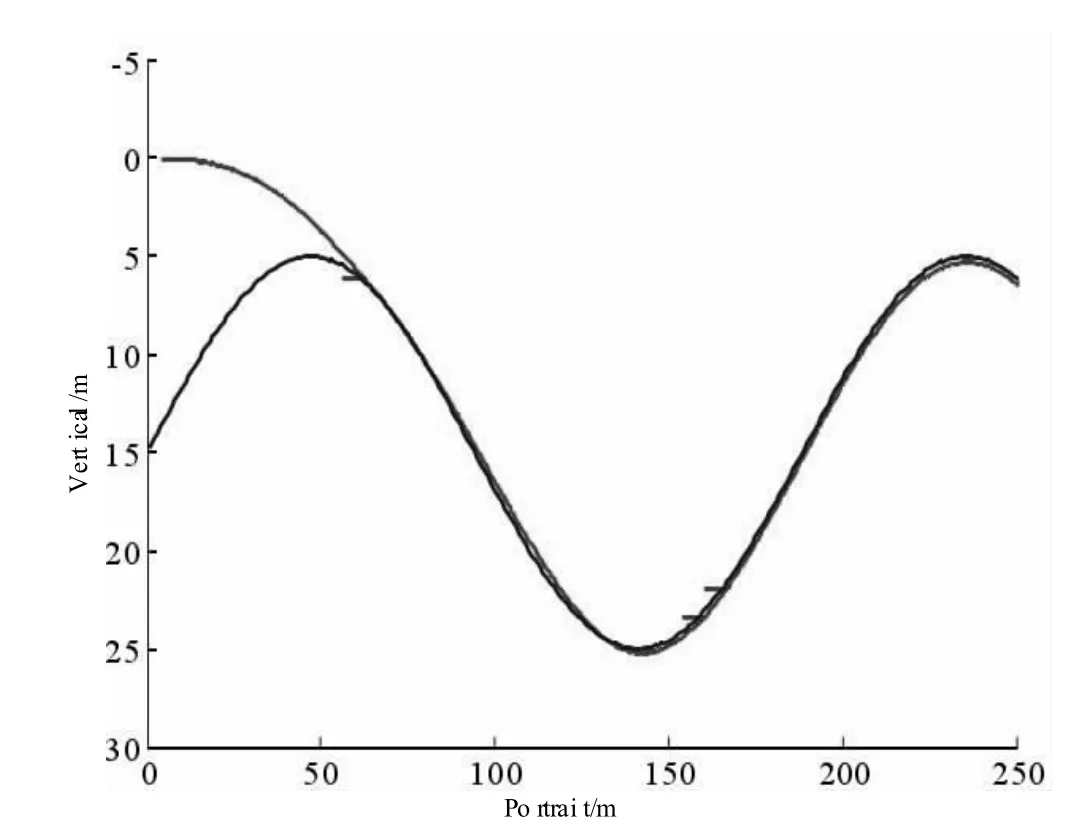
图5 正弦路径跟踪曲线

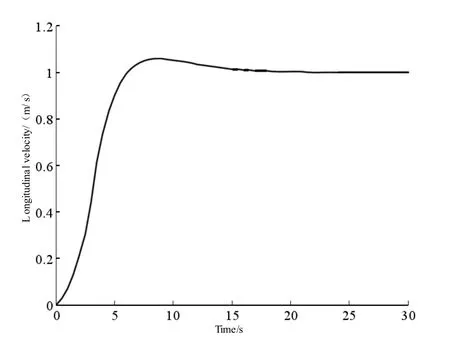
图6 正弦纵向速度控制曲线

5 结论

水下潜器的欠驱动控制技术已经在基础理论研究与实践运用方面获得了一定成绩,欠驱动工业机器人的非线性空间公平、非线性能控性与结构能控性的理论研发也获得了很大发展,但相关理论还在不断发展完善，水下潜器欠驱动控制理论体系仍有较大发展空间和不足，如因为欠驱动系统的非完整约束带来的下潜器无法实现跟踪全坐标空间轨迹曲线等问题亟需解决。此外，欠驱动水下潜器空间目标跟踪问题需要引入更丰富的设计方法进行工程验证。故, 进一步提出新的控制方式和理论方法,不断发展应欠驱动水下机器人技术的理论体系,并进行系统运动规划与轨迹追踪工程实践, 是欠驱水下潜器研究的新发展趋势。