挤压工况下方形锂电池模组等效建模及参数反求

徐峰祥，田浩东，段利斌，杨智辉，石 磊，吴 闯

(1.武汉理工大学 汽车工程学院，武汉 430070；2.江苏大学 汽车与交通工程学院，江苏 镇江 212013；3.宝山钢铁股份有限公司研究院，上海 201900；4.汽车用钢开发与应用技术国家重点实验室(宝钢)，上海 201900)

随着电动汽车的快速发展，锂离子动力电池以其高能量密度、高充电效率、长循环寿命等优点而被广泛应用[1]。随着对电动汽车续航里程的要求不断提高，增大锂离子电池能量密度成为最直接有效的途径之一。目前，对电池单体在机械滥用下的研究较多，对模组研究较少。本文研究一种电池模组等效建模方法，探究动力电池在不同方向上受到挤压冲击载荷后的机械变形和力学响应，为研究电池模组在机械变形下的损伤及简化建模仿真提供实际的参考。

近年来，面对电动汽车频发的事故，许多学者围绕机械滥用下电池单体及模组的损伤进行了探索研究，在进行数值模拟分析时，合适的有限元模型对仿真预测的效果至关重要。目前，锂离子电池的有限元建模策略主要有3种：① 精细化建模。完全按照电池内部组成进行建模，能模拟出挤压下电池内部各层的失效破坏形式及力学响应，模型精度非常高，但计算非常耗时，实际分析中较少采用这种建模策略。② 代表性体积单元建模。将电池组分等比例在厚度方向放大，可以大概模拟出电池最终各层的破坏形式，精度较高，计算耗时一般。Amodeo等[2]研究了方形锂离子电池模组在准静态和动态平面压缩试验下的力学响应，并对模组采用代表性体积单元的建模策略进行仿真模拟，仿真与实验结果有较高的一致性。Wang等[3]探究了在不同的机械加载情况下，18650圆柱电池单体的机械响应及电化学响应，并建立了代表性体积单元的有限元模型，对电池单体的短路行为进行了较为准确的预测。③ 均质等效建模。用一种材料的结构模型代替电池所有组成成分，可以模拟出电池整体的机械变形及力学响应，计算效率很高。兰凤崇等[4]研究在挤压试验下软包电池的力学响应特性，并建立均质各向同性的电池内芯模型，较好地表征了试验结果。在实际的电动汽车碰撞事故中，一般是基于电池模组甚至整个电池包进行安全评估研究，而实际的电池模组结构复杂，按照模组内部实际结构建立有限元模型进行仿真模拟，工作量巨大且耗费大量的计算资源，因此，有必要建立一种简化的等效模组。

本文以方形三元锂电池模组作为研究对象，基于LS-DYNA和HYPERMESH联合仿真，建立精细化电池模组，沿模组的长、宽和高3个方向施加不同挤压载荷；建立了模组等效模型，以模组外壳厚度和电芯的本构模型参数为设计变量，借助LS-OPT软件进行参数反求，得到最优的变量，在提高计算效率的前提下，较为准确地模拟出精细化模组在挤压冲击下的力学响应。

1 电池模组结构及等效机理

电池模组一般由通过汇流排串并联连接在一起的多个单体电池、压板、隔板、支架、上盖和底板等组成，不同形状结构的单体电池排布成组方式不尽相同，但核心均以电池的串并联排布为主。

电池内芯由于其特殊的结构形式而具有各向异性，一方面由于具有多孔性的高分子聚合物隔膜和金属集流体均为各向异性材料，另一方面是电池内芯的分层叠片结构引起的各向异性。目前多采用代表性体积单元建模策略进行较为细致的建模，但在实际试验中，获取内芯组成部件的力学材料参数时，集流体和活性物质材料粘结为一体，不易获取单独组分的材料参数，通常采用半均质化模型建模。在考虑计算效率且主要关注的是电池的整体变形及力学响应时，一般可将电池内芯简化成各向异性的均质材料模型。内芯分层复合材料均质化原理如图1所示。

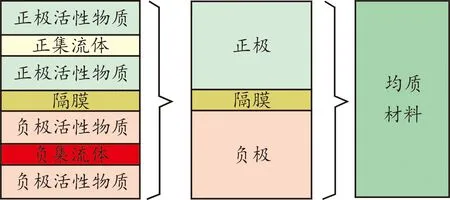
图1 电池内芯分层复合材料均质化原理

在研究模组受挤压时，对单体电池内部结构的关注并不高，精细化模组模型的单体电池可采用均质化模型。根据等效简化程度，分别建立半均质和均质化等效模组模型，前者将精细化模组的所有单体电池等效为同一材料模型，后者将精细化模组的所有组成部件等效为同一材料模型，如图2所示。通过参数反求方法得到最佳等效模组材料本构模型和等效模组外壳厚度，使等效模组在不同方向的挤压冲击载荷下能较为准确地模拟出精细化电池模组力学响应，提高计算效率。

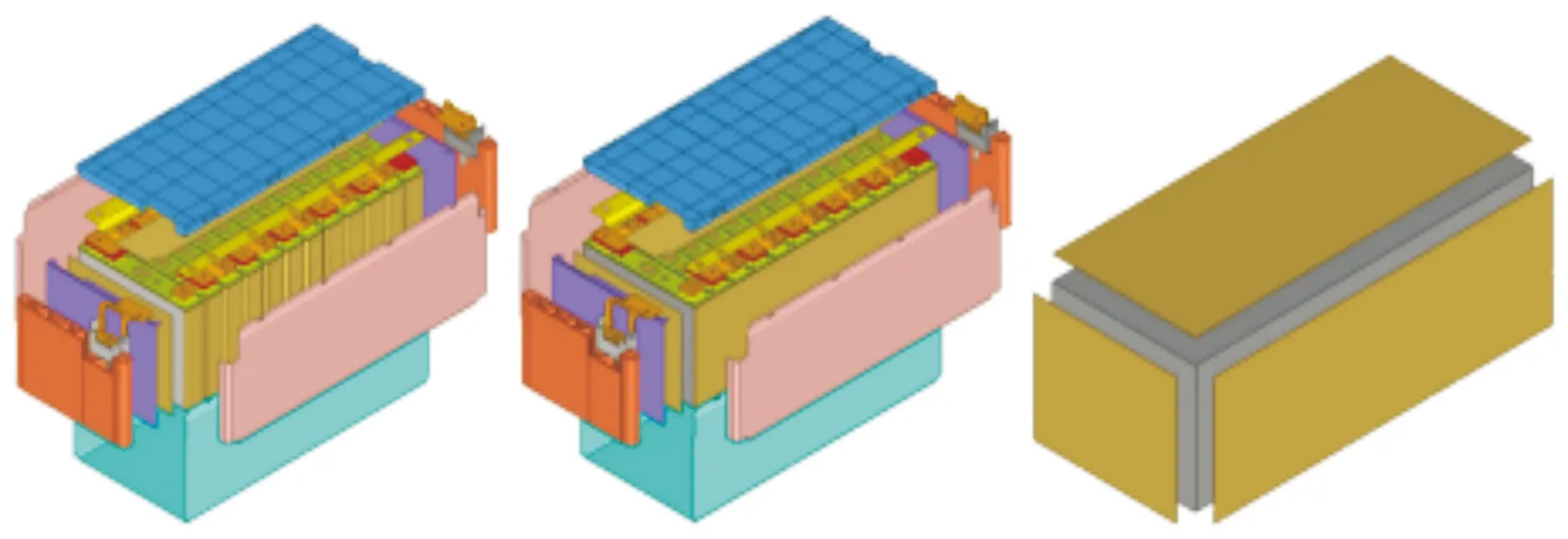
图2 精细化-半均质化-均质化模组等效示意图

2 碰撞挤压模型构建

2.1 精细化模组建模

方形电池模组结构主要包括上盖、汇流排、绝缘压板、电池端子、单体电池、电池外壳、端板、侧板等，如图3所示。单体电池之间采用胶粘连接，金属件的连接以点焊为主。塑料上盖和绝缘压板夹在传输电流的汇流排上下两侧，起到绝缘保护作用；电池四周的侧板起到固定防护和散热的作用；端板起到载模组端子和固定模组的作用。

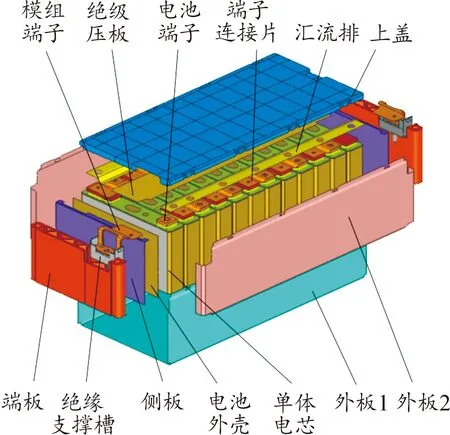
图3 精细化模组结构

电池模组的结构复杂，尤其是对电池内芯的模拟更是难点，选择合适的材料本构才能真实模拟挤压碰撞过程中电池的变形损伤，提高仿真精度。Lars等[5]在研究圆柱18650钴酸锂电池时，根据力学试验结果发现电池的力学性能与可压缩泡沫材料的本构模型相似，提出了σ=A+Bεn的均质本构模型。杨博达[6]分析了在LS-DYNA中5、14、26、126、63、163、75、144和154号9种不同的泡沫材料的特性，指出126号蜂窝铝材料对各向异性材料有比较准确的模拟效果。罗海灵[7]在研究软包电池内芯均质化建模时，认为电池结构不同方向上的力学性能差异较大，在LS-DYNA中采用126号蜂窝铝材料建立电池的完全均质化模型。因此，本文对电池内芯采用均质化建模方法，运用LS-DYNA材料库中的蜂窝铝材料，基于σ=A+Bεn建立材料本构模型，建立精细化有限元模型。

方形电池模组的各部件单元模拟类型及相应的力学性能材料参数如表1所示。绝缘支撑槽采用四面体单元模拟，端板、电池端子和电芯采用六面体单元模拟，其他部件采用壳单元模拟。考虑电池外壳对内芯的影响，对电池外壳采用全积分计算[8]，NIP积分点设置为5，ELFORM设置为16，其余壳单元采用缩减积分计算，NIP积分点设置为3，ELFORM设置为2。

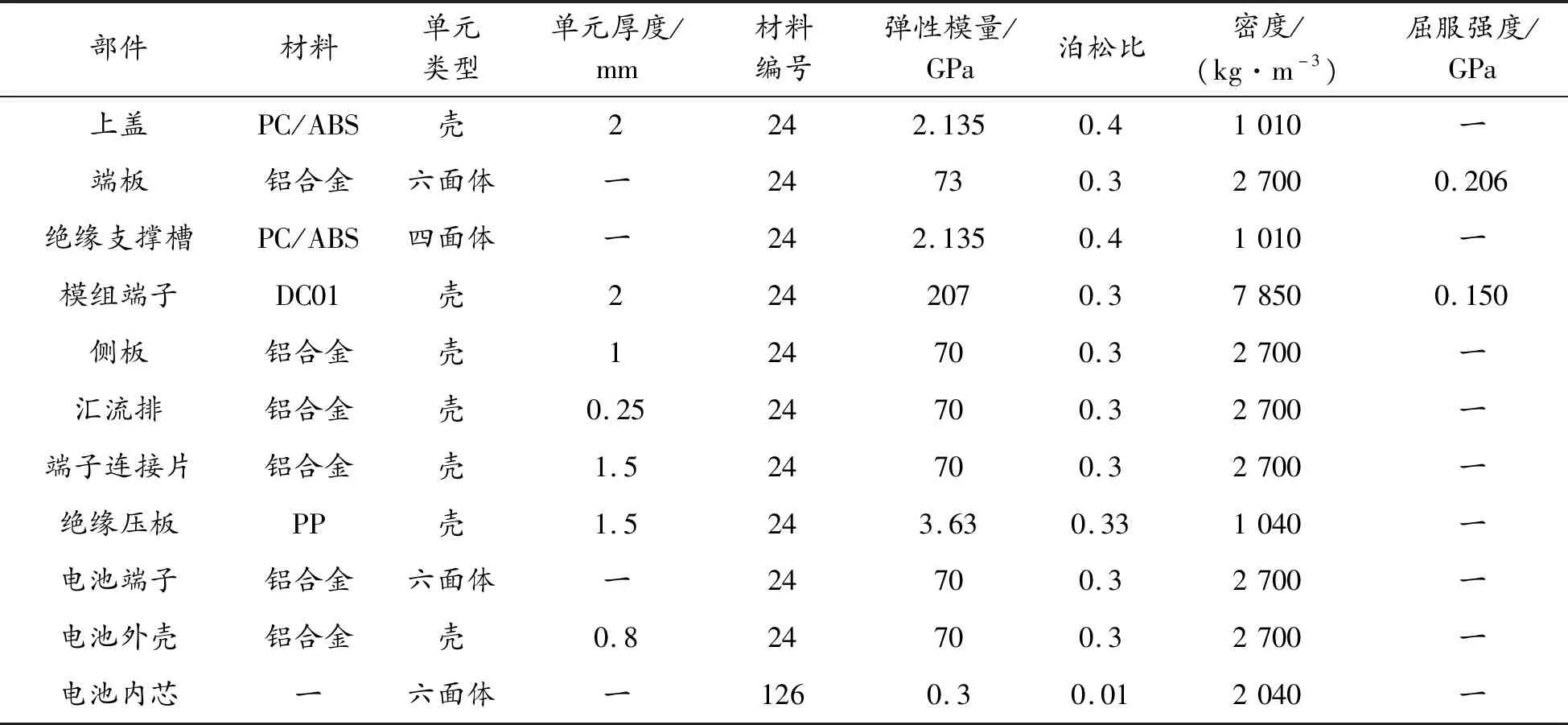
表1 各部件单元模拟类型及材料参数

电芯采用LS-DYNA中的126号蜂窝铝可压缩性泡沫材料模拟，该材料需要在3个材料方向上分别输入正应力-应变曲线与剪应力-应变曲线进行模拟，各个方向上的应力分量相互解耦。应力-应变本构参考软包三元锂电池的本构模型[9]，如图4所示。

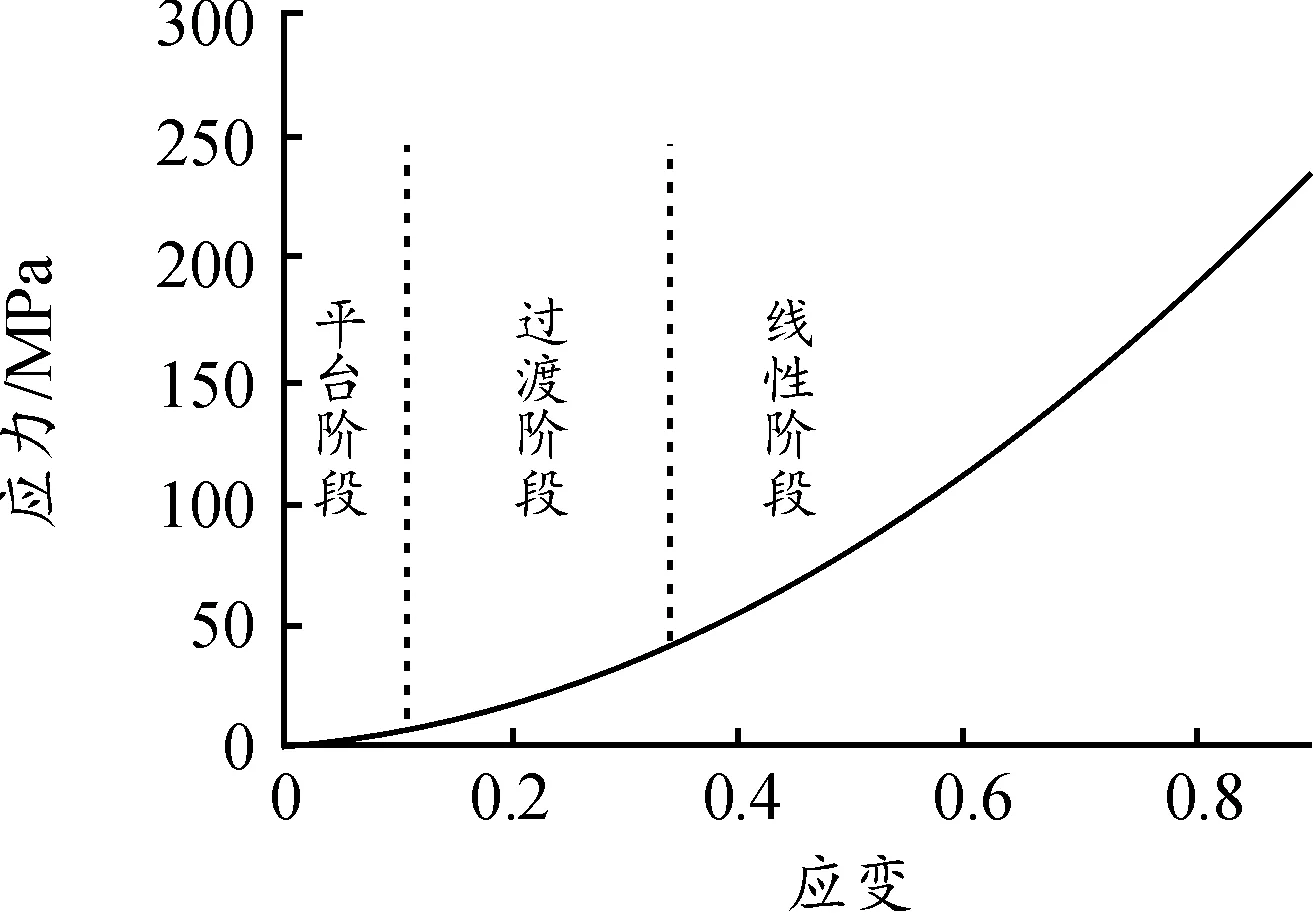
图4 软包三元锂电池本构模型

在正向的挤压条件下，剪切方向所受应力较小，以较小的恒定应力值输入模拟。电池内芯在压缩过程中，先经历初始平台阶段，主要是电池外壳变形抵抗挤压力，然后进入过渡阶段，电池内芯的多孔材料逐渐压实提供支持力，最后进入线性阶段，内芯完全压实，应力应变呈指数相关[10]。采用RgdBody刚性连接模拟汇流排和电池端子之间的螺栓，模组侧板和隔板的点焊用RIGID刚性连接模拟。

2.2 半均质化模组建模

由于精细化模组中多个单体电芯、电池外壳排列连接建模复杂，半均质化模组等体积的用单个大电芯及模组外壳代替原有的多层排列结构，不仅减少了建模工作量，同时简化了单体电池之间的粘胶连接等，提高了计算效率。模组其余部件及连接方式与精细化模组保持一致，同时调整等效电芯的密度使半均质化模组的总质量接近精细化模组，保证等效模拟效果更为准确，半均质化模组的结构如图5所示。

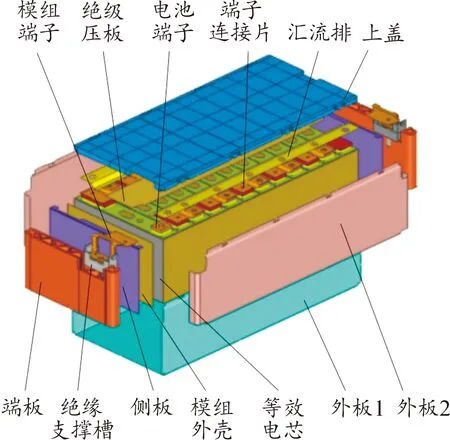
图5 半均质化模组结构

2.3 均质化模组建模

均质化模组采用一个近似等体积的方形模组块和外壳进行等效建模，如图6所示。由于电池模组内部主要组分为多个串并联的单体电芯，均质模组材料模型和精细化模组电芯保持一致，同样调节等效模组材料密度，使均质化模组的总质量和精细化模组趋于一致，使等效模拟效果更为精确。

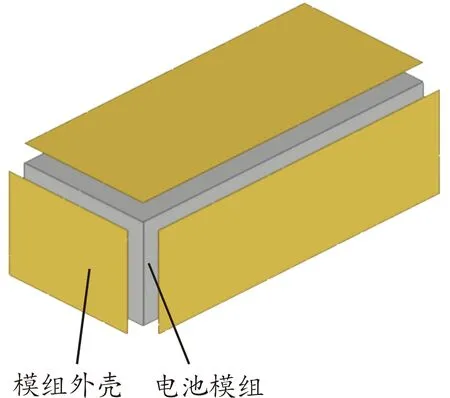
图6 均质化模组结构

3 参数反求

3.1 挤压工况

在碰撞挤压方案方面，定义沿着模组内单体电池厚度排列方向为X向，侧面沿电池面内方向为Y向，底面沿电池面内方向为Z向，电池模组不同方向的加载工况参数如表2所示。加载工况中，刚性柱、刚性球均采用壳单元建模，半径为75 mm，为提高计算效率，刚性柱、刚性球均取1/2模型。

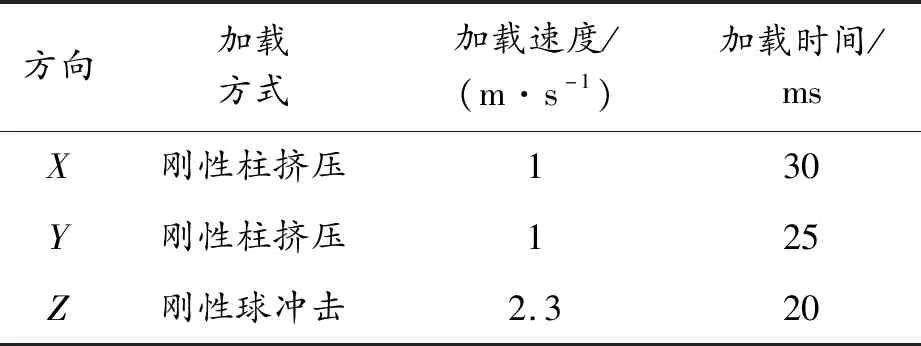
表2 模组不同方向的加载工况参数

为便于观察，X、Y向取1 m/s作为准静态恒定挤压速度，Z向模拟低速冲击工况，刚性球配重150 kg，冲击初速度为2.3 m/s。分别建立精细化模型X、Y、Z向的挤压冲击有限元模型，如图7所示。添加刚性墙合理约束模组的移动自由度，刚性柱、刚性球和模组之间采用Automatic Surface To Surface接触，模组内部组成设置Automatic Single Surface接触，接触摩擦因数设为0.2。

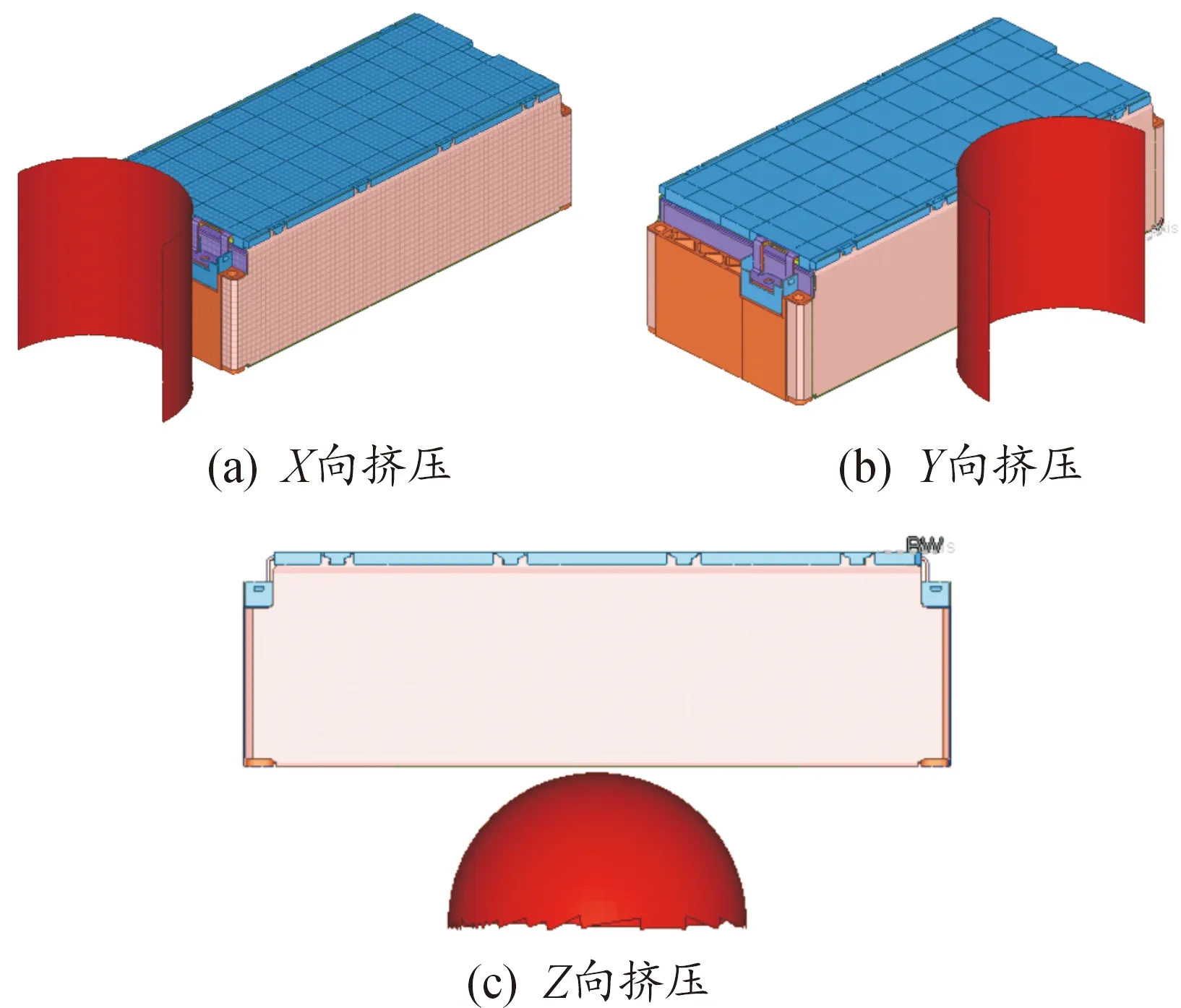
图7 精细化模型的挤压冲击有限元模型

为分析对比等效模拟的效果，等效模组同样设置X、Y、Z方向相同的挤压冲击工况。

3.2 反求原理

由于在精细化模组模型中，单体电池所占体积质量比例远超其余部件，在碰撞挤压工况下，电池相关材料参数的改变对模组的力学性能影响最大。材料的力学特性主要是基于本构模型参数决定，调节材料不同应变状态下的应力值能使等效模组更好地模拟精细化模组挤压下的力-位移载荷，但工作任务量巨大且违背了等效建模提升计算效率的初衷，故采取对本构模型的应力值进行整体缩放的策略，同时便于参数变量的选取设计。而电池外壳作为电芯最直接的防护件，对电池的力学性能也起到重要作用，故进行等效模拟时可将电芯的本构模型应力值缩放系数和模组外壳厚度作为参数变量。通过比较等效模组在碰撞挤压下和精细化模组力-位移曲线的误差值判断变量设计的好坏，借助LS-OPT软件将参数反求问题转化为优化问题，进而获取模型设计参数[11]。

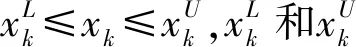
图8 电池设计参数反求流程框图

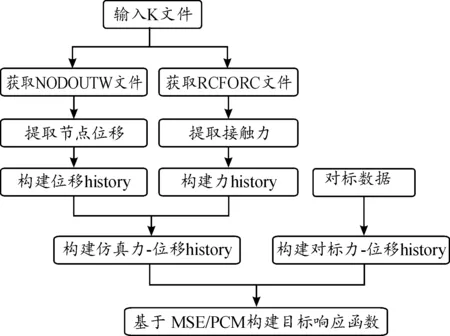
图9 目标函数的构建流程框图

在模组不同的碰撞工况下，分别对等效模组设计变量的优化范围进行定义，如表3所示，SFO为电芯本构应力值的缩放系数，T1为模组外壳的厚度。

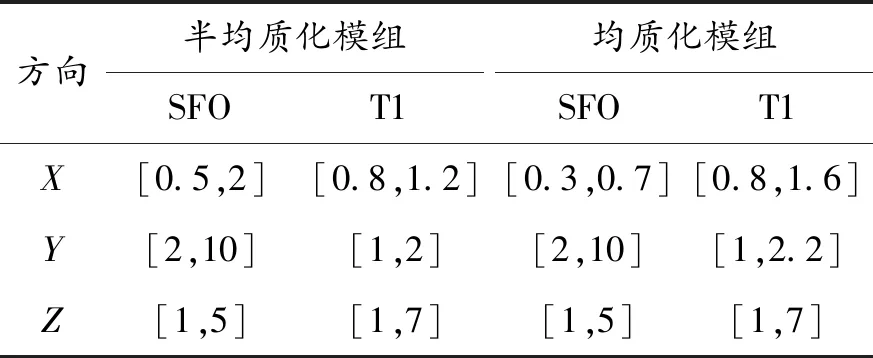
表3 设计变量优化范围的定义

在X和Y方向上，根据曲线总体单调变化的特性，以精细化模组的力-位移曲线和均质化模组仿真的力-位移曲线的均方误差最小为优化目标，优化方程定义如式(1)所示。

(1)

在Z方向上，由于需要观察电池模组在冲击后的变化，电池存在一个力回弹阶段，整体力-位移曲线并非呈现单调变化趋势，曲线之间可能存在迟滞现象，MSE误差算法基于曲线之间的纵向误差的拟合逼近效果较差，采用基于PCM部分曲线映射的方法进行曲线逼近。在匹配曲线长度不同或存在迟滞时，PCM部分曲线映射法将较短的目标曲线通过一定的缩放变换映射到另一曲线上，计算对应目标点映射路径和匹配曲线之间围成的面积并进行求和得到εp，εp最小即为曲线之间误差最小的最佳匹配。

在LS-OPT中，采用基于代理模型的优化方法，选取径向基函数构建代理模型，使用空间填充的采样方法，每次迭代选取5个仿真点。选择默认高效率的带域缩减序列策略，逼近缩放参数和振荡收缩参数取0.8，平移收缩参数取1。采用ASA和LFOP混合算法对基于MSE/PCM的目标函数进行优化[12]，等效模组优化流程如图10所示。

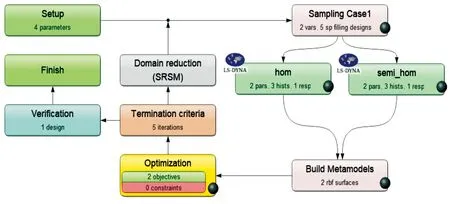
图10 等效模组优化流程框图

3.3 参数优化结果

LS-OPT运算后提供所有迭代计算的文件，从优化结果的文件lsopt_report中读取不同方向上等效模型设计变量SFO和T1的最优解，如表4～6所示，即为要求解的等效模组的最佳参数值。

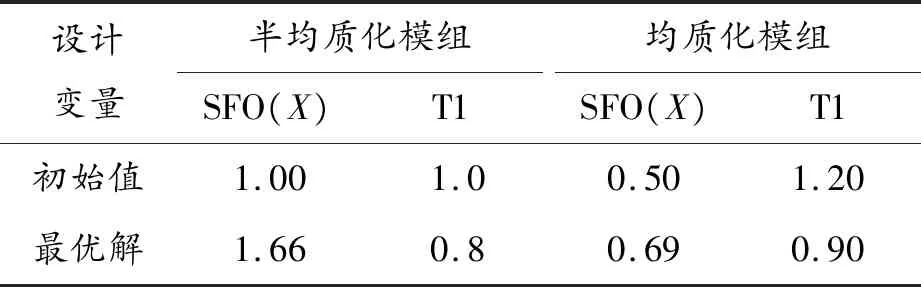
表4 X方向参数优化结果

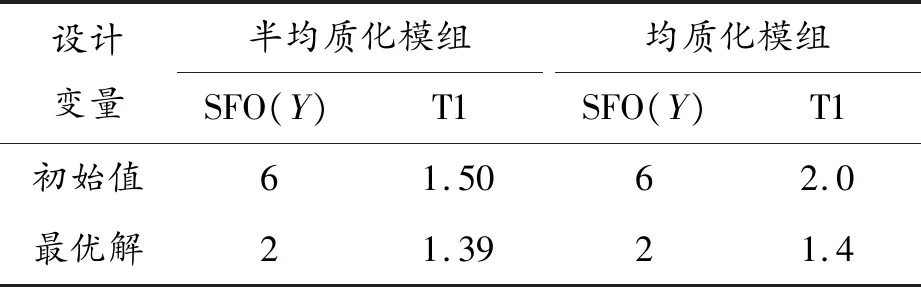
表5 Y方向参数优化结果

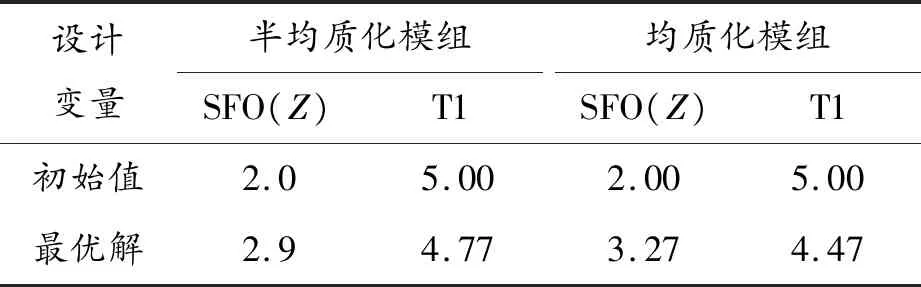
表6 Z方向参数优化结果

在lsopt_report文件中可以比较分析经过优化后，最优解下等效模组MSE/PCM误差值相较于初始解下的缩减程度，如表7～9所示。

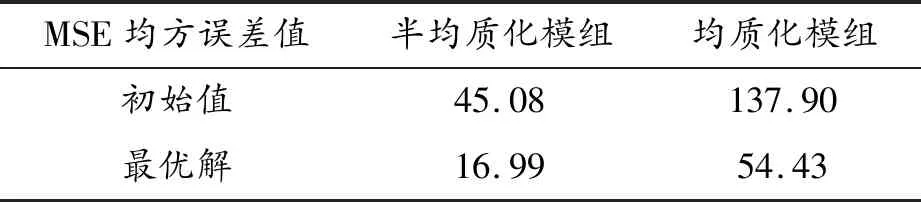
表7 X方向参数优化结果

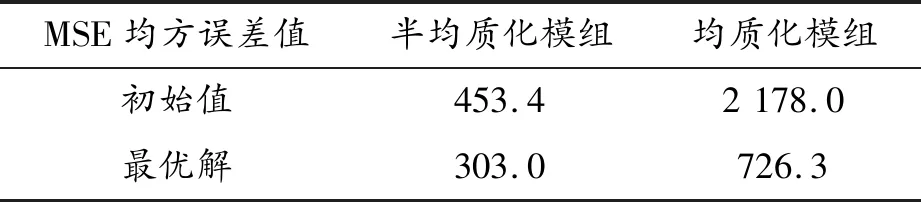
表8 Y方向参数优化结果

表9 Z方向参数优化结果

4 对比与讨论

4.1 仿真精度对比

LS-OPT在迭代运算中会将每次仿真计算的结果保存下来，通过HYPERVIEW后处理软件查看最优解的结果文件，获得等效模组在X、Y、Z方向上受到机械加载后的变形情况和载荷变化曲线。

在X、Y、Z方向受到挤压冲击后，在挤压结束时刻和冲击载荷最大时刻，3种类型电池模组受到最大机械载荷时的变形对比情况，如图11所示。

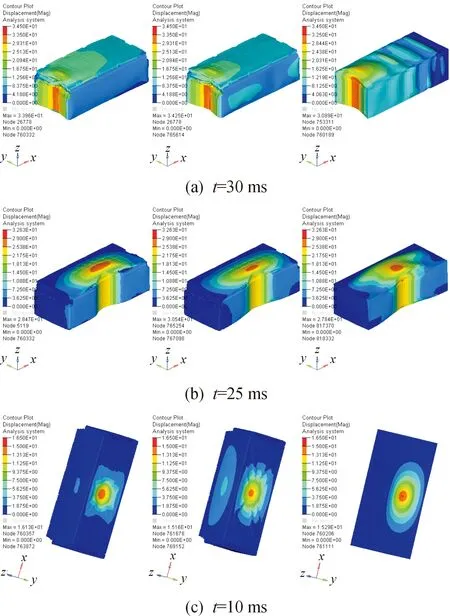
图11 不同方向上 3种类型电池模组受到最大机械载荷时的变形对比

电池模组在X方向沿电池堆叠受到静态挤压时，端板首先受到刚性柱的挤压，侧面外板端部和端板通过焊接连接，从而使侧面外板发生弯曲变形，随后上盖受到挤压产生弯曲变形，此阶段主要为金属件的弹性变形。接着内部电池变形主要承受挤压载荷，在挤压结束时刻，半均质化等效模型由于只对内部电池模型进行简化，基本和精细化模组的变形一致；均质化等效模型对整个电池外部部件都进行了简化，变形和精细化模组略有差异。电池模组在Y方向受到挤压时，侧面外板和上盖先受到挤压产生变形，然后主要由内部电池产生变形抵抗挤压力。由于侧面外板较薄且和内部电池之间几乎没有间隙，半均质化等效模型和均质化等效模型都能较好地模拟出精细化模组挤压后的变形模式。电池模组在Z向底部受到刚性球冲击时，主要由内部电芯承受冲击载荷，等效模型受到冲击后的变形形式和精细化模组的变形基本一致。

研究电池模组在受到挤压冲击下的力-位移曲线有助于了解电池模组的力学响应行为，图12是在不同方向受到载荷冲击后精细化模组和等效模组载荷变化曲线的对比图。

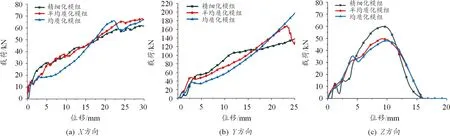
图12 不同方向受到载荷冲击后精细化模组和等效模组载荷变化曲线

在X向挤压工况下，在0～5 mm的变形阶段内，精细化模组端板及上盖主要进行承载，金属产生弹性变形抵抗挤压力，力曲线接近线性增长；之后主要由电池变形进行承载，曲线呈现类似蜂窝铝材料挤压后的力学特性。半均质化模组等效拟合精度较高，均质化模组也基本能拟合出精细化模组的载荷位移曲线。在Y向挤压工况下，在挤压变形为0～3 mm的阶段，侧板较薄，抵抗变形能力相对于端板较弱，初始力曲线线性增长阶段较短。电池模组内部电池间一般用粘胶粘接而成，沿单体电池粘接平面方向进行挤压时，当挤压力大于电池之间的粘力时，主要集中在挤压处的部分单体电池发生变形，等效模型受到挤压后会整体变形，随着挤压的进行，等效模组的受力会大于精细化模组，在20 mm变形内等效拟合精度较高。在Z向冲击载荷下，模组受到动态冲击后力曲线上升较快，而在卸载阶段，部件在弹性变形范围内的变形消失，电池模组的力曲线均呈线性下降趋势。等效模组能较好地预测精细化模组的载荷变化趋势且能较为准确地模拟出峰值载荷出现时刻。

电池模组结构复杂，在研究实际整个电池包碰撞分析过程中，更加关注电池模组的整体变形和力学响应[13]。利用参数反求的方法建立等效电池模组模型，半均质化模组在节省一定计算时间的条件下，能较为准确地模拟出精细化电池模组的力学响应特性，均质化等效模组能极大地提高计算效率，但拟合精度也有所下降。

4.2 效率对比

不同模组的单元总数及计算时长如表10所示。精细化模组单元总数达165 577，X、Y、Z方向挤压工况计算总时长为289 min，半均质化模组单元数缩减为118 261，计算总时长为152 min，相较于精细化模组，计算效率提升了47.4%，均质化模组单元数仅为8 502，效率提升了96.5%。

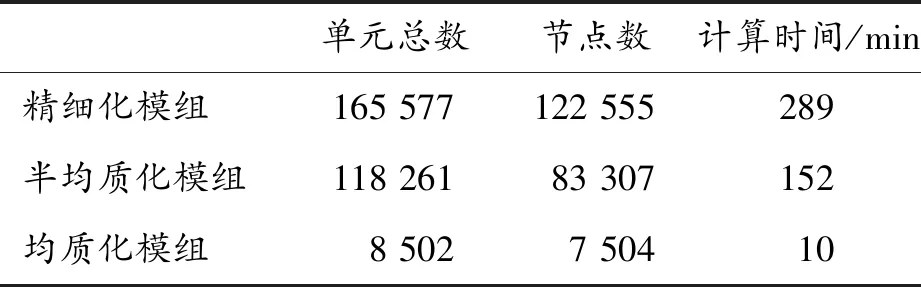
表10 不同模组单元数量和计算时间

等效模组基本能拟合精细化模组挤压状态下的力学响应，且能缩短仿真计算时间。半均质化模组等效模拟精度较高，相较于精细化模组计算效率有一定程度的提升；均质化模组极大地简化了模组的结构，精度方面有所下降，但极大地提升了计算效率。

5 结论

针对现阶段动力电池在机械滥用的情况下产生机械损伤甚至引起热失控的安全性问题，以及计算机仿真模拟的效率问题，提出了一种电池模组等效建模的方法，将精细化电池模组等效简化为半均质和均质化2种类型模组，在平衡仿真精度和效率提供了不同的选择。对比研究在不同的挤压碰撞工况下，精细化和等效模组的力学响应特性，基于参数反求的方法，建立了最优的等效模组，表征精细化模组在受到机械载荷下的变形及力学响应。研究结果为探究电池模组级别的等效建模方法及最优设计参数的反求提供了参考，对实际进行电池模组的仿真模拟对标具有参考意义。

1)基于有限元仿真建立精细化电池模组，对精细化电池模组进行不同程度的简化建立半均质和均质化模组，在相同的机械挤压工况下，等效模组基本能表征出精细化模组在机械挤压工况下的变形和力学响应行为。

2)采用参数反求的方法，以精细化模组在机械挤压下的力学响应曲线为参照目标，设置等效模组的电池材料本构模型和外壳厚度为设计变量，基于曲线匹配之间的误差最小，迭代反求设计变量的最优解，得到较优的等效模组模型，为变量设计类问题提供了参考意义。

3)在实际工程设计中，电池包的概念化开发阶段可采用均质化建模策略，在保证一定精度的前提下大幅缩短开发周期；在工程电池包开发的详细阶段可采用半均质化建模方式，保证较高精度的同时提高计算开发效率。