Unity3D随机寻路算法设计
2022-01-13史宝明贺元香
史宝明,贺元香,李 岚
(兰州文理学院 数字媒体学院,甘肃 兰州 730010)
在进行Unity3D游戏开发过程中,物体在场景中随机游走是经常要实现的功能,常见的游戏对象游走通常设置固定的线路,让游戏对象沿着指定的轨迹行进,这种方法易于实现,因而在游戏场景中较为常见,并且这种方式可以沿着地形精确的绘制游走路径,灵活的控制和调整游走对象在游走路径不同位置的角度、速度等参数,使得游走动作连贯、逼真.但是这种方式由于游走路线固定不变,游戏对象每次游走的路径都一样,游走行为一成不变,导致游戏交互中缺乏随机性和趣味性.另外一种游走是通过设计寻路算法来实现,如Unity3D中的导航网格寻路[1-2]以及文献[3-6]中所研究的算法,这种方式行走路径由智能算法随机产生,每次行走的路线是随机的.但是游戏对象按这种方式游走时,需着力解决游戏对象在不同地形影响下的角度、速度匹配问题以及转身问题,否则有可能出现游走动作未匹配地形,或者游戏角色在转身过程中的动作怪异或不连贯,导致游走行为出现Bug,因此有必要深入探讨游戏对象在游戏场景中的随机寻路算法.
1 理论基础
随机寻路算法的实现要着力解决游走对象在行进过程中的角度控制问题和速度控制问题.角度控制实际上就是控制对象的选择,这涉及欧拉角和四元数的转换问题,角色行走过程中的速度控制问题考虑通过插值运算函数来解决.本节通过深入讨论欧拉角、四元数、插值运算等相关的数学理论和应用,来设计实现随机寻路算法.
1.1 欧拉角与四元数
Unity3D游戏开发中,随机游走时要时刻根据地形调整移动对象的角度,这涉及对象的旋转控制问题,常用的角度旋转表示方法一般有欧拉角和四元数.欧拉角是指在三维空间通过指定与三个旋转轴相关联的三个角度来表示任意方向的方法,是用来表示三维坐标系中方向和方向变换的,由章动角、旋进角和自转角三部分组成.欧拉角表示角度直观方便,但采用不同的轴序旋转有可能会造成不同的旋转结果,因此需要按指定的轴序进行旋转,并且当在旋转过程中如果发生旋转轴和坐标轴重合的情况时,会引起万向死锁,这时会丢失一个方向上的旋转能力,也就是说在这种状态下无论怎样旋转都无法得到想要的旋转效果.
由于欧拉角旋转可能出现万向死锁问题,因此Unity3D游戏开发中更为常用的是四元数旋转.四元数是由爱尔兰数学家哈密顿在1843年发明的数学概念[7].其本质是一种高阶复数,可以表示一个四维空间.四元数旋转可以避免万向死锁现象、方便快捷,能提供平滑的插值效果,并且通常比矩阵旋转的效率高,在游戏开发中有着广泛的应用[7-9].
1.2 插值运算
游戏开发中当游戏对象在场景中随机游走时,游戏对象位置和角度会发生实时变化,通常采用逐帧更新的方式来改变对象的位置和角度,而位置和角度的确定一般通过已知的起始点和确定的目标点来进行逐帧计算得到,这就需要用到插值运算.
Unity3D的线性插值函数Lerp()可以实现两个材质之间、两个向量之间、两个浮点数之间、两个颜色之间的插值运算.在随机寻路算法中,随机游走对象位置的变化、角度的旋转都可采用插值运算来实现,这样可避免生硬的角色移动和旋转,让移动、旋转的动作保持连贯.Unity3D中的插值函数可表示为
F=Lerp(start,end,t).
(1)
其中:start为插值的起始值;end为插值的终止值;t为插值点,其取0到1之间的浮点数.start和end的取值可为材质、浮点数、二维向量、三维向量和颜色值等,这里着重使用向量的插值运算.
2 总体设计思路
随机寻路算法主要包括随机游走范围的产生、随机产生目标点、位置偏移更新和角度偏移更新等几个部分.整个随机寻路算法的设计如下:
Step1 场景初始化,确定游戏对象随机游走的范围.
Step2 在游走范围内随机产生一个新目标点.
Step3 游走对象从当前位置开始,采用插值函数来逐帧更新对象的位置和角度.
Step4 判断游戏对象是否到达目标点,如果到达目标点,则跳转到Step2;否则计算位置偏移值和角度偏移值,调整游戏对象的位置和角度后,返回Step3.
整个随机寻路算法的程序流程如图1所示.

图1 随机寻路算法流程Fig.1 Flow chart of random routing algorithm
3 算法详细设计
3.1 产生随机游走范围
游戏对象随机游走范围的确定通过定义一个public类型的Rect对象moveRect来进行限定,moveRect对象需要设置根坐标(x,y)和宽高(width,height)来定义一个矩形区域(见图2),游戏设计过程中可根据游戏对象在场景中的位置来确定moveRect对象的初始化参数.并可使用Gizmos对象的DrawWireCube()方法绘制立方体线框将矩形区域显示出来.
3.2 随机产生目标位置
在生成的矩形区域中随机生成一个点作为目标位置targetPos,目标位置的确定方法如下:
targetPos.x=Random.Range(moveRect.xMin,moveRect.xMax),
targetPos.z=Random.Range(moveRect.yMin,moveRect.yMax).
其中:moveRect.xMin3,moveRect.xMax,moveRect.yMin,moveRect.yMax分别为矩形对象moveRect在x,y方向上的最小值和最大值.Random.Range()方法则是在指定的一个区间内返回一个随机值.一般游戏对象是确定其在xz平面上的随机位置,而矩形对象采用的是xy坐标平面,因此这里进行简单的变换,将矩形区域的y值赋值给游戏对象的z坐标值.当游戏对象移动到目标点后,自动生成下一个目标点,反复此过程,直到程序结束为止,详细游走过程成如图2所示.
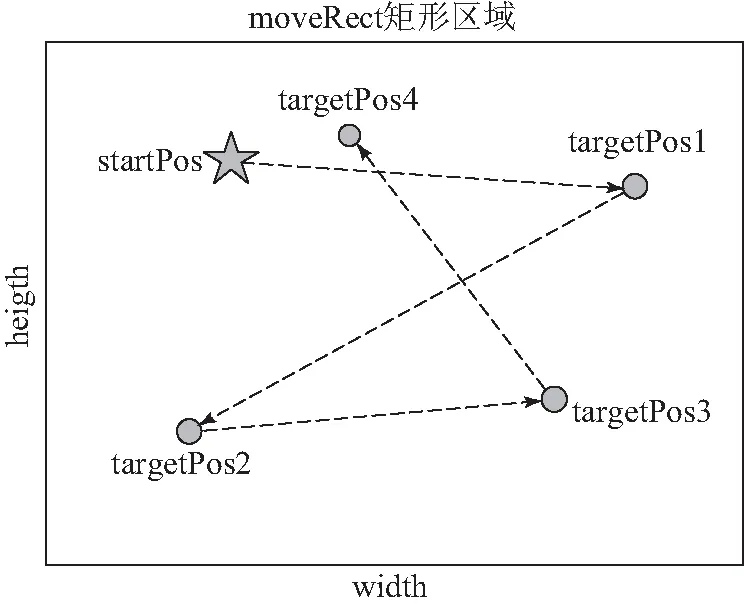
图2 随机游走示例Fig.2 Random walk example map
3.3 位置偏移更新
3.3.1 逐帧匀速更新
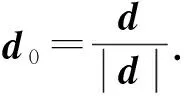
pcurrent=pcurrent+d0×s,
详细的位置偏移更新情况如图3所示.
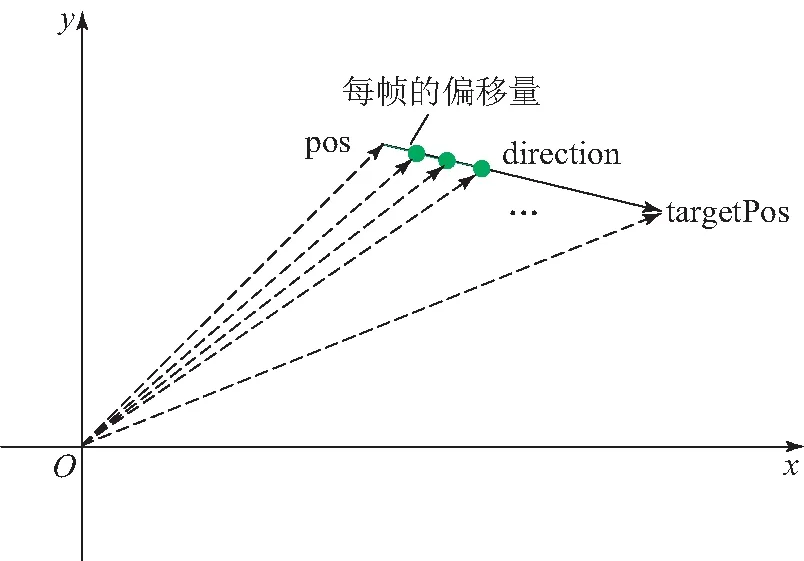
图3 位置偏移更新Fig.3 Position offset update map
这种逐帧更新的方法虽然看似是匀速的,实际上由于每帧的执行时间长短不一样,并不能得到真正意义上的匀速移动,因此实际应用中一般采用插值运算来进行位置更新.
3.3.2 插值运算更新
当确定了游戏对象的初始位置pstart和目标位置后ptarget,可以使用插值运算的方式来实现对象位置的平缓移动,假设从开始帧到当前帧的执行时间为Δt,速度控制参数为s,根据式(1)则有
pcurrent=Lerp(pstart,ptarget,Δts).
其中速度控制参数s由游戏对象运动的总时间决定,这种方式可有效克服每帧执行时间长短的差异对物体移动速度的影响.
3.4 角度偏移更新
游戏对象在进行角度偏移更新时,旋转偏移通常要借助欧拉角和四元数的转换来完成,以下为欧拉角与四元数的详细转换过程.
欧拉角一般用一个三维向量(θ,φ,ψ)来表示,其中θ,φ,ψ分别表示沿坐标轴x,y,z三个轴的旋转角度.而一个四元数可以表示为
q=w+xi+yj+zk.
其中:w,x,y,z为实数;i,j,k为三个虚数单位,并且满足:
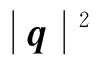
四元数被广泛应用在计算机图形学中表示三维空间的旋转操作.在Unity3D游戏开发中,通常用四元数来表示游戏对象的旋转.
通过指定的旋转轴和沿该轴旋转的角度α可以构造一个四元数,其表示为
w=cos(α/2),x=sin(α/2)cos(βx),y=sin(α/2)cos(βy),z=sin(α/2)cos(βz).
其中:α为沿指定的旋转轴旋转的角度;βx,βy,βz分别为该旋转轴在x、y、z轴上的分量.
一个欧拉角(θ,φ,ψ)可通过式(2)转换为一个四元数
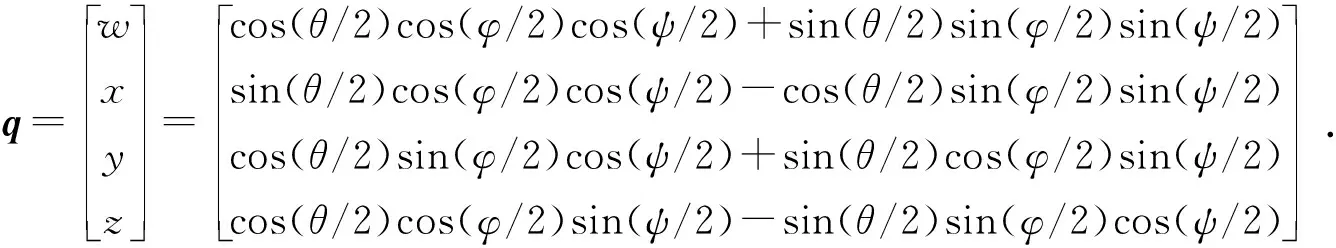
(2)
而一个四元数q=[w,x,y,z]T可通过式(3)转换为一个欧拉角
(3)
一般而言,游戏对象的朝向都是面向移动方向的,当游戏对象到达一点,再重新向一个新的目标点移动时,就涉及对象角度旋转的问题,也就是对象的转身问题.转身过程一般在较短的时间内完成,通常采用角度插值运算的方式来进行转身角度更新.假设qcurrent为游戏对象当前位置的角度值,qtarget为目标点角度值,Δt为开始帧到当前帧的执行时间,θ为旋转速度控制参数,根据式(1)有
qcurrent=Lerp(qcurrent,qtarget,Δtθ),
其中游戏对象旋转速度的快慢由旋转速度控制参数θ决定.
另外,由于Unity中游戏对象的rotation属性是用四元数来表示的,而对象在旋转时,通常更为直观的表示方式是欧拉角形式,可通过Quaternion.Euler()方法在四元数和欧拉角之间进行转换,再进行应用,具体转换过程参考式(2)和式(3).
欧拉角旋转容易引起万向死锁,而四元数对于数值计算的偏差不敏感,数值上的小误差引起的只是旋转姿态小的调整.在计算机游戏和动画设计中,采用四元数容易实现对摄像机及游戏对象角度的连续微调,并可避免欧拉角旋转产生的万向死锁问题.
4 实验
4.1 实验环境

4.2 实验仿真与分析
为了直观的演示游戏对象的随机游走,通过在随机游走所经过的路径上标注小球的方式来标识游戏对象的移动路径,其中灰色小球序列为物体逐帧走过的路径,灰色大球为目标点序列.初始化时,设置游戏对象游走的范围、游走速度.开始时,自动生成第一个目标点,当游戏对象移动到该目标点时,会自动生成下一个新的目标点,如此反复,可以实现游戏对象随机游走的功能,图4和图5为两次程序运行的结果.
可以看出,图4(A)、图5(A)为游戏对象运动到第1个目标点,并自动生成第2个目标点的状态,图4(B)、图5(B) 为运动到第2个目标点,并自动生成第3个目标点的状态,图4(C)、图5(C) 为运动到第3个目标点,并自动生成第4个目标点的状态,图4(D) 和图5(D)为运动了一段时间后的状态.可以看出,当前一个目标点路径与下一个目标点路径的夹角较大时,两条路径之间的路径过渡为圆弧状,表明角度的偏移在不断地进行更新,即游戏对象在路径转弯处的角度在不断地迭代变化.
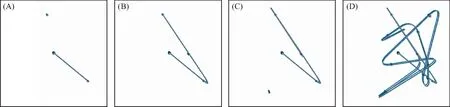
(A) Frame 73;(B) Frame 222;(C) Frame345;(D) Frame1200图5 第二次运行结果Fig.5 Second run results
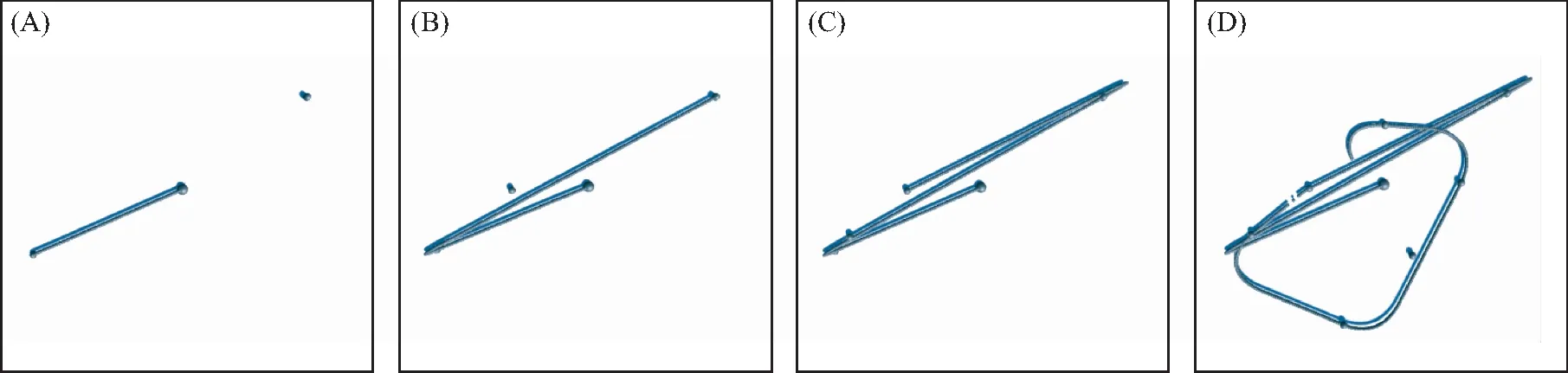
(A) Frame 75;(B) Frame 239;(C) Frame 380;(D) Frame 688图4 第一次运行结果Fig.4 First run results
5 结语
将随机寻路算法编写为一个脚本,挂在游戏对象上,就可以灵活的实现场景中游戏对象的随机游走,大大方便和简化了游戏开发中随机游走功能的实现过程,因而具有广阔的应用前景.需要注意的是,在进行位置更新和角度更新时,当物体在坡度平缓的地面上移动,可以得到很好的效果,当物体在坡度较大且地形复杂的地面上移动时,可通过将目标路径进行细分的方式来逐段控制物体的移动,使得在局部范围内保持地形变化一致,进而解决游戏对象未能和地面很好贴合的问题.
