高土石坝坝坡地震失稳风险评估
2022-01-13杜全胜吕小龙迟世春邢建营
杜全胜,吕小龙,迟世春,邢建营
(1.黄河勘测规划设计研究院有限公司,河南 郑州 450003;2.水利部黄河流域水治理与水安全重点实验室(筹),河南 郑州 450003;3.大连理工大学建设工程学部水利工程学院,辽宁 大连 116024)
0 引 言
高土石坝坝坡的抗震稳定性一直是土石坝工程中的重大课题之一。国内外学者采用刚体极限平衡法、有限元等确定性分析方法进行坝坡抗震稳定性研究,已取得了大量研究成果和工程经验。陈祖煜[1]指出,把结构可靠度理论作为建立岩土工程风险控制标准的依据,将成为科学、定量地研究和保证工程结构安全性的重要手段。
土石坝地震反应分析中存在的不确定性因素,包括地震的不确定性和筑坝堆石料参数的不确定性等。邵龙潭等[2]采用随机地震反应分析方法计算土石坝的随机动力反应,但未考虑筑坝料参数的不确定性;刘晓等[3]根据边坡动力反应的能量分布特征,对持续时间统计窗进行统计分析,计算边坡的可靠度指标;杨鸽等[4]采用局部平均细分法模拟高堆石坝的物理力学性质随机场,分析筑坝料不确定性对土石坝地震反应的影响。文献[3- 4]的研究实质是对地震响应随机过程进行概率分析,以获得可靠度指标。上述方法只采用某一种特定的地震波,且未考虑地震发生的不确定性。
本文将基于概率烈度对应的地震动作为拟静力法分析的输入,采用蒙特卡罗法考虑筑坝料参数的不确定性,计算坝坡地震失稳风险概率。最后,应用上述方法计算了紫坪铺大坝在设计基准期内的坝坡地震失稳概率。
1 高土石坝坝坡地震失稳风险分析方法
我国将地震烈度作为地震区划的强度指标。因此,可建立如下高土石坝坝坡地震失稳概率模型
(1)
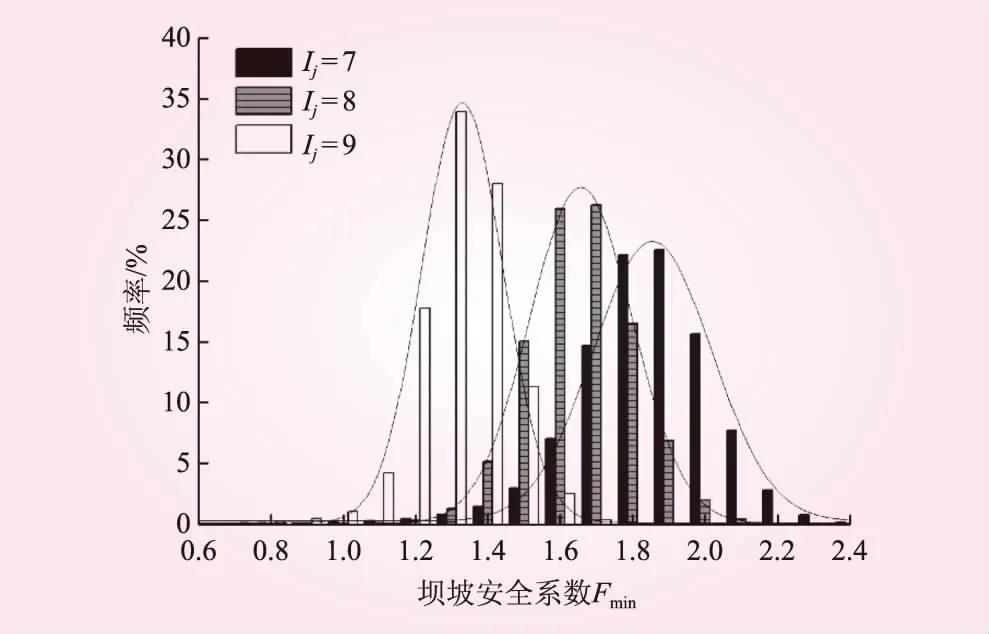
式中,pf(R R-S=Fs(X)-Fcri=0 (2) 式中,X为具有不确定性的筑坝料参数;Fs为根据X确定的安全系数;Fcri=1.0。 通过对我国大量地震资料的分析显示,在50年设计基准期内,场址区地震烈度符合极值III型概率分布[5]为 (3) 式中,ω为地震烈度的上限值,取为12;ε为众值烈度,取为场址区的基本烈度减去1.5;K为形状系数。 地震的发生概率与工程的设计基准期密切相关,若已知T年内的烈度概率分布函数,则任意t年内的地震烈度概率分布函数为 (4) 对于设计基准期为100年的水工建筑物,地震烈度的概率分布表达式为 (5) 坝址发生烈度I地震的概率为 p(I)=FⅢ(I+1)-FⅢ(I) (6) 根据地震工程学,地震烈度是凭地震发生时各类建筑物反应、损坏程度、地表变化状况确定的,是对地震灾害的一种宏观评价。因此,地震烈度与加速度峰值之间没有直接对应关系。但是通过对国内大量地震资料统计分析,表明场址区的加速度峰值a可用地震烈度I表示[6]: a=10(Ilg2-0.01) (7) 对于高土石坝坝坡,极限状态方程没有显示表达式,因此不能采用一次二阶矩进行计算。Monte-Carlo法适用于求解隐式功能函数的可靠性问题,但当失效概率很小时,Monte-Carlo法的抽样次数非常大。由于对坝坡进行稳定性分析时,需要对每次抽样得到的样本,采用智能优化算法搜索最危险滑弧的位置,计算量将会呈级数增长,限制了该方法的使用。 高斯过程(GPs)是在贝叶斯学习理论基础上,发展起来的一种机器学习方法。与人工神经网络(ANN)、径向基函数(RBF)、支持向量机(SVM)相比,高斯过程模型具有对模型参数依赖性弱,对小样本、非线性问题泛化能力强的优点[7]。本文将采用高斯过程响应面拟合极限状态方程,并结合Monte-Carlo法计算坝坡的地震失稳概率。 假设样本的总容量为N,抽取的第k个样本为Xk,则坝址区发生烈度为Ij地震,高土石坝坝坡的失稳概率为 (8) 式中,G(·)为土石坝坝坡是否失稳的状态函数,表达式为 (9) 高土石坝坝坡地震失稳风险计算流程如图1所示。首先,采用坝址地震风险评估模块,计算坝址区发生各级地震的概率。然后,在地震作用下坝坡失稳概率评估模块中,考虑筑坝料参数的不确定性,结合构造的高斯过程响应面,计算各级地震烈度下,坝坡的失稳概率。最后,通过式(1)将上述两种不确定性耦合起来,综合确定坝坡的地震失稳概率。 图1 高土石坝坝坡地震失稳风险评估流程 具体流程为①根据场址区的地震安全性评价报告,确定坝址区的基本烈度,计算地震烈度Ij的发生概率p(Ij)。②根据加速度峰值与地震烈度的关系(式(7)),计算地震烈度Ij对应的峰值加速度。③根据工程设计资料,确定坝坡典型剖面尺寸,选取筑坝料参数的统计量。④根据文献[8]的研究成果,堆石料的抗剪强度参数φ0服从正态分布,Δφ服从对数正态分布[8]。若筑坝料参数X包括n个随机变量xi,在[μi-fσi,μi+fσi]等间距抽取2f+1个样本,组成总容量为(2f+1)n的学习样本集。⑤根据筑坝料参数的统计特征,随机抽取Ntest个样本,组成测试样本集。⑥对学习样本集和测试集的每一个样本,采用智能优化算法搜索坝坡最危险滑弧的位置和安全系数Fs,min。⑦基于学习样本集的计算结果,构造高斯过程响应面,建立筑坝料参数与坝坡安全系数之间的映射关系。⑧通过收敛判别条件,决定是否需要更新响应面。遍历测试样本集的所有样本,若测试样本不满足收敛条件,则将该个体加入学习样本集,返回④;若所有测试样本均能满足收敛条件,则转入步骤⑨。⑨根据筑坝料抗剪强度参数的统计特征,随机抽取N=107个样本,结合已建立的高斯过程响应面,利用式(8)计算发生烈度Ij地震时的坝坡失稳概率。⑩根据式(1) 综合确定坝坡的地震失稳概率。 第⑧步的收敛判别条件为由于高斯过程模型能同时给出预测变量的均值μFs和标准差σFs,因此本文以Fs,test是否能够落在区间[μFs-2σFs,μFs+2σFs]作为收敛判别条件。若预测失败,则将该样本加入学习样本集,重新构造响应面。通过反复迭代,使响应面不断逼近极限状态方程。 在正常运用期,库水和面板对上游坝坡具有明显的约束作用,即使坝址区发生地震,上游坝坡也不易失稳。因此,本次计算仅分析紫坪铺大坝的下游坝坡的地震失稳概率。 紫坪铺混凝土面板堆石坝的最大高度为156 m,坝顶宽12 m,上游坡比为1∶1.4,下游坝坡在二级马道以上为1∶1.7,二级马道以下为1∶1.4。坝址基本烈度为VII度,工程按照8度地震进行设防。考虑到设计烈度为6度的土石坝,地震一般不是工程设计的控制荷载,仅采取适当抗震措施即可保证工程安全,即当地震基本烈度小于VII度时,pf[Fs(x) 表1 紫坪铺大坝坝址区发生烈度地震的概率 在堆石坝施工过程中,监理将对堆石料的填筑密度进行严格的抽检,可认为堆石料容重的变化很小。然而,由于堆石坝工程规模宏大,上坝料来自不同料场和料场的不同部位,母岩性质和沉积条件差异较大,这些因素都将造成堆石料抗剪强度指标的不确定性。 本次坝坡稳定计算,堆石料采用非线性强度准则,即 φ=φ0-Δφlg(σ3/pa) (10) 式中,φ0和Δφ为堆石料的非线性强度参数;σ3为小主应力;pa为标准大气压。为了计算方便,本文对主、次堆石料采用相同的抗剪强度指标。通过统计国内大量堆石料的三轴试验成果,选定抗剪强度指标的统计特征参数见表2。 表2 抗剪强度指标的统计特征参数 (°) 根据《碾压式土石坝设计规范》,采用筑坝料的小值平均值进行下游坝坡的稳定计算。图2为确定性分析结果,①②③分别是地震设防烈度Ij=7、8、9度时的潜在滑动面。由图2可知,随着地震从7度增大到9度,滑动面切割坝坡位置逐渐变浅,且滑出点逐渐升高至二级马道高程。地震设防烈度为7、8、9度时,坝坡的最小安全系数Fs,min列于表3。如表3所示,当地震设防烈度Ij=7时,最小安全系数为1.58,说明坝坡在7度地震作用下,尚有充足的安全裕度。当地震设防烈度Ij=9时,最小安全系数为1.24,已逼近规范的临界值。考虑到在地震过程中,高土石坝坝顶的加速度较大,是工程的薄弱部位,因此应在坝顶区域采用阻滑钢筋网、浆砌石护坡等综合防护措施保证坝坡的抗震安全。 图2 确定性分析对应的滑弧 表3 确定性分析求得的地震安全系数 基于堆石料抗剪强度参数的统计特征,抽取107个样本,结合构造的高斯过程响应面,计算所有样本的安全系数,然后按区间分别统计各地震烈度下,坝坡安全系数的分布情况。图3为地震设防烈度Ij=7、8、9度时坝坡最小安全系数的频率分布。可知,在各地震烈度下,考虑筑坝料抗剪强度指标的不确定性,坝坡最小安全系数可采用正态分布拟合。经K-S法检验分析,坝坡的安全系数服从正态分布。 图3 不同地震设防烈度下坝坡安全系数频率分布 将计算结果汇总于表4。如表所示,坝址处发生7度地震的概率为15.94%,在7度地震作用下,坝坡失稳的概率仅为8.27×10-4。反之,坝址处发生9度地震的概率仅为0.26%,但相应的坝坡失稳概率将大幅提高,达到1.49×10-2,大约提高两个数量级。另外,坝址处发生8度地震的概率为2.80%,相应的失稳概率为6.29×10-3,综合失稳概率为1.76×10-4,明显大于7度和9度的综合失稳概率,表明紫坪铺面板坝采用8度设防的经济合理性。考虑筑坝料参数和地震不确定性的综合失稳概率为3.47×10-4,各烈度条件下坝坡的地震失稳概率基本属于同一数量级,说明在高土石坝坝坡地震失稳风险分析中综合考虑堆石料和地震的不确定性十分必要。 表4 地震作用下坝坡失稳概率 在岩土工程中,一般以年计失效概率作为风险控制标准,且《水利水电工程结构可靠性设计统一标准》的可靠度指标也是由年计失效概率确定的。因此,通过下式将失效概率换算为年计失效概率: (11) 式中,T为水工建筑物的寿命;Nd为结构的设计基准期。由于水利工程规模宏大,寿命一般较长,可认为T远大于Nd。因此,从偏于安全角度出发,令T=Nd,紫坪铺大坝的设计基准期为100年,则坝坡的年计失效概率为3.47×10-6。 为便于定量评价边坡的可靠度水平,将失效概率换算为可靠指标β=-Φ-1(Pf)。本次计算得到的紫坪铺大坝坝坡抗震稳定可靠指标β为4.56。根据规范,可靠度指标应满足β≥βt,βt为目标可靠指标。《碾压式土石坝设计规范》规定,1级水工建筑物,安全级别为I级时,坝坡抗滑稳定的目标可靠指标为4.2。综上,可认为紫坪铺大坝坝坡地震失稳风险能够满足规范要求。 (1)本文提出的高土石坝坝坡地震失稳风险评估方法能够同时考虑地震和筑坝料参数的不确定性。工程算例表明,该方法具有较高的计算效率,为评估实际高土石坝坝坡地震失稳概率提供了一条有效的分析途径。 (2)采用地震烈度作为地震危险性的宏观衡量尺度,通过引入地震烈度概率模型,将基于概率烈度的地震动作为拟静力法分析的输入,使得坝坡地震失稳风险分析更加全面。采用蒙特卡罗法内嵌高斯过程响应面法的方式考虑筑坝料参数不确定性的影响,该模式实现容易,计算效率较高,便于实际工程应用。 (3)地震具有不确定性和随机性的双重性质。拟静力法无法将地震的随机性(随机的地震波形)纳入考虑,且未反映筑坝料参数空间变异性的影响,上述问题的解决尚需进一步研究。1.1 场址地震烈度概率模型
1.2 地震烈度时高土石坝坝坡失稳概率
2 计算流程
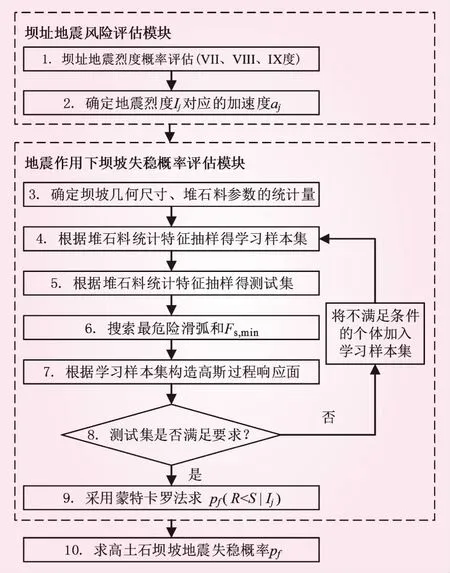
3 工程算例




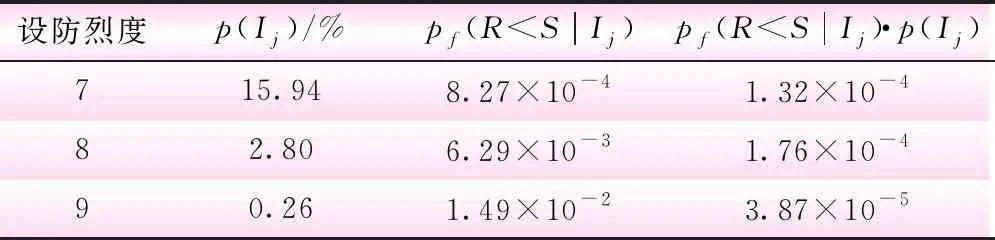
4 结 论
