基于DBSCAN聚类和数据筛选的系统谐波阻抗估算

雷达，常潇，刘子腾，赵军，张世锋，徐永海

(1. 国网山西电力科学研究院， 太原 030001； 2. 华北电力大学 新能源电力系统国家重点实验室，北京102206)

0 引 言

随着电力电子器件和电力设备的发展，谐波污染问题越来越严重，若不进行治理，会给电网带来很大威胁[1-3]。公共连接点(Point of Common Coupling，PCC)处的谐波通常是由系统侧和用户侧叠加产生的，准确划分谐波责任是控制谐波水平的重要前提，而系统阻抗又是谐波发射水平评估和谐波责任划分的关键参数[4-7]。

目前国内对谐波阻抗估算已经进行了大量研究。波动量法[8-9]适用于背景谐波电压较平稳的情况，该法通过计算PCC处谐波电压和电流波动量比值来求解系统阻抗。独立随机矢量协方差特性法[10]通过数学变换的方法削弱背景谐波电压波动项，对背景谐波电压小范围波动有一定的抑制作用。盲源分离类算法[11-12]对谐波电压和谐波电流进行分离，通过混合矩阵和谐波阻抗矩阵之间线性关系求得系统侧谐波阻抗，要求源信号具有非高斯性且相互独立。线性回归法[13-15]利用戴维南或诺顿等值电路中PCC处谐波电压和谐波电流关系式，回归出系统阻抗值。随着新能源的高占比入网，加剧了电网背景谐波的波动情况，使背景谐波电压可能发生谐振等短时较大幅度电压波动[16-17]，上述方法在处理较大范围谐波电压波动时效果不佳，此时需要经过数据筛选，才能更准确估算谐波阻抗值。

同时，以上研究均基于系统阻抗恒定的假设。由于等值电路中通常将除关注用户外的区域计入系统侧，因此电力系统运行方式的改变、无功补偿方式的变化、投切支路、分布式电源脱网与并网等原因都可能导致系统阻抗发生变化，在计算谐波阻抗时，应首先分析系统阻抗值是否发生变化。

考虑阻抗变化的谐波阻抗估计研究较少，文献[18]通过加窗一元线性回归粗估系统谐波阻抗，再用小波变换模极大值法检测系统谐波阻抗突变点，但当背景谐波电压波动较大时，系统谐波阻抗粗估值误差大，此时会干扰对测量数据的分段处理，从而不能精确辨识突变点。文献[19]提出一种基于斜率辨识谐波阻抗变化的方法，在谐波电压和谐波电流散点图中，通过计算斜率值区分阻抗值，但仅适用于背景谐波电压平稳的条件。

考虑系统谐波阻抗变化和背景谐波电压波动的情况，采用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)聚类[20-21]分离出谐波阻抗恒定的数据组，再根据复相关性分析筛选出背景谐波电压较稳定的数据段，最后采用稳健回归法估算系统阻抗。文中方法中，DBSCAN是一种密度类聚类算法，其相较于划分和层次聚类法，在非球状分布散点图的聚类中具有明显优势；复相关性分析可以对多因变量进行总体相关性分析；稳健回归法能根据数据的残差分配权重，减弱异常点对数据的影响，可使结果更加精确[22]。

1 谐波阻抗估算模型

在谐波阻抗估计中，通常将除关注用户以外的区域全部等效为系统侧，可得图1所示的等效电路图。

图中，Us和Ic分别为代表系统侧等效谐波电压源和用户侧等效电流源；Zs和Zc分别为系统侧和用户侧等效谐波阻抗；Upcc和Ipcc分别为PCC处的谐波电压和谐波电流。根据图1可列关系式：

UPCC=ZSIPCC+Us

(1)

根据式(1)将各变量实部和虚部分开，得：

(2)

式中带有下标x和y的变量分别为其复数形式的实部和虚部。如果Zs和Us均为变量，则难以估算Zs的值，因此，需要筛选出系统阻抗恒定和背景谐波电压波动较小的数据段，再进行阻抗估计。

图1 等效电路图Fig.1 Equivalent circuit diagram

2 考虑阻抗变化和背景谐波电压波动的谐波阻抗估算

2.1 DBSCAN聚类筛选

当系统谐波阻抗变化时，需要将不同系统阻抗值对应的数据段区分开，否则会存在很大误差[23-25]。提出基于DBSCAN聚类的数据分类方法，将系统阻抗相同的数据组聚成一簇，再对每个簇分别进行阻抗估算。

根据式(1)可以看出，以|Ipcc|为横坐标、|Upcc|为纵坐标构成的散点图成条状分布，其斜率与系统阻抗值有关，截距与背景谐波电压有关，图2为系统阻抗变化2次构成的散点图，图中有3个长条状分布，分别对应3个系统阻抗值。

图2 谐波电压与谐波电流散点图Fig.2 Spot diagram of harmonic voltage and current

常用的聚类方法大多基于距离聚类，其聚类结果通常是以点为中心的球状簇，当数据呈非球状分布时，难以达到预期效果。DBSCAN是一种典型的基于密度的聚类算法，通过寻找高密度区域将数据点分成不同的簇，在DBSCAN聚类中将核心点定义为在对象半径Eps内含有超过最小数目MinPts的点，该点都在簇内，而边界点和噪音点是簇外的点，其中对象半径Eps和最小数目MinPts为给定值。

DBSCAN聚类步骤如下：

(1)数据集D中的所有对象标记为未处理状态；

(2)检查数据集D中的每个对象p的Eps邻域NEps(p)，检查NEps(p)包含的对象数是否小于最小数目MinPts，如果是进入步骤(3)，如果否进入步骤(4)；

(3)标记对象p为边界点或噪声点；

(4)标记对象p为核心点，并建立新簇Ci，将NEps(p)中未归入任何一个簇的对象加入Ci；

(5)检查是否所有对象p已经归入某个簇或标记为边界或噪声点，如果否,回到步骤(2)，如果是，输出结果。

2.2 复相关性分析筛选原理

进行聚类后，对每个簇分别求解谐波阻抗值。当背景谐波电压存在较大范围波动时，难以精确估计系统阻抗的值，为了提高估算精度，提出基于复相关性分析的数据段筛选方法。

复相关系数能反映因变量和全体自变量之间的线性关系，以式(2)中第一个式子为例，Upcc-x为因变量，Ipcc-x和Ipcc-y为自变量，其值越趋近于1表明Upcc-x和Ipcc-x和Ipcc-y整体的相关性越高，而由式(2)可知背景谐波电压波动较小时，其线性关系强烈，复相关系数接近1，此时估计出的谐波阻抗值较精确。反之，越趋近于0,表明相关性越低。故可通过筛选谐波电压和电流具有较高复相关系数的数据段，来提高谐波阻抗估算值的精确程度。

以y代表Upcc-x，x1和x2代表Ipcc-x和Ipcc-y，计算因变量y与其他两个变量x1,x2总体的相关程度，需要构造一个关于x1,x2的线性组合，用y对x1,x2做回归得到：

(3)

(4)

式中R为y和x1,x2间的复相关系数。

保留R趋向于1的数据段，即筛选出背景谐波电压波动相对较小的谐波电压和谐波电流组。

2.3 基于bisquare权重的稳健回归法

为减小“异常点”的作用，提出在DBSCAN聚类和复相关性筛选后采用基于bisquare权重的稳健回归法进行系统阻抗估算。

稳健回归法根据各数据点残差不同施加不同的权重wi，是一种特殊的加权最小二乘估计，数据点残差越大，所分配的权重值越小。该法能通过不断迭代改进权重系数，可以有效减弱“异常点”的作用。当背景谐波波动时，稳健回归具有明显优势。其优化的目标函数为：

(5)

采用式(6)所示bisquare法定义权重：

(6)

式中c为常量，一般取4.685；ui为标准化的残差指标；s为残差尺度。

ui=ei/s

(7)

s=MAD(e1,…,en)/0.6745

(8)

MAD(e1,…,en)=Median|e1-Median(e1,…,en)|

(9)

这里，Median为变量的中位数。

稳健回归具体步骤如下：

(2)利用式(11)和式(12)计算标准化残差u，将其带入式(10)中，并化为对角线权向量W；

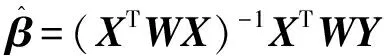
2.4 谐波阻抗估算流程

提出的谐波阻抗估算方法流程图如图3所示。

在谐波阻抗估算中，首先采用DBSCAN聚类将谐波阻抗相同的数据组筛选到一起，再对每个组根据式(3)和式(4)进行复相关性分析，筛选出背景谐波电压较稳定的数据段，最后估算系统阻抗值。

图3 谐波阻抗估算流程Fig.3 Flow chart of harmonic impedance estimation

3 实验结果与分析

搭建如图1所示的等效电路图，以5次谐波为例，设定用户侧5次谐波等效阻抗值为150+j 200 Ω，用户侧等效电流源谐波发射均值3+j2 A；系统侧阻抗t0时刻为1+j2 Ω，t1时刻变化到4+j3 Ω，在t2时刻变化到5+j4 Ω，系统侧谐波电压均值分别为2+j3 V，在谐波源中加入大小不等的波动，仿真共取800个样本点，t0、t1和t2分别对应样本点0、 400和600。

3.1 系统阻抗改变点辨识

将所提出的DBSCAN辨识系统阻抗变化方法与文献[18]提出的小波辨识法(方法1)和文献[19]提出的斜率辨识法(方法2)作对比。

对于方法1，根据文献[18]，测量PCC处5次谐波电压和谐波电流矢量值，计算系统阻抗粗估值见图4。

图4 系统阻抗粗估值Fig.4 Rough estimation of system impedance

再对系统阻抗粗估值做小波变换，提取高频分量d1和d2的波形如图5所示。

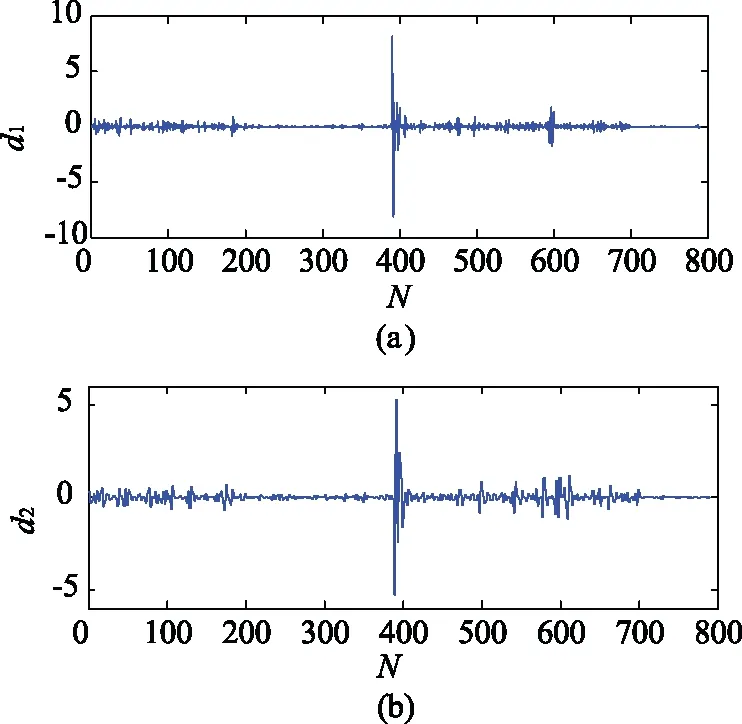
图5 高频分量Fig.5 High frequency component

计算高频分量d1中突变点为391、 393和397，d2中突变点为391、 392、 395和396，这与设定的400和600这两个突变点不相符，其原因在于t2时刻突变前后系统阻抗值变化较小，且背景谐波电压波动的干扰较大，因而方法1失效。

对于方法2，根据文献[19]，获得以|Ipcc|为横坐标、|Upcc|为纵坐标的散点图如图6所示，计算图6中每相邻两点之间的斜率值，如图7所示。

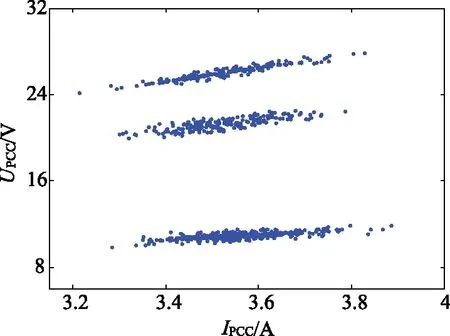
图6 散点图Fig.6 Scatter plot

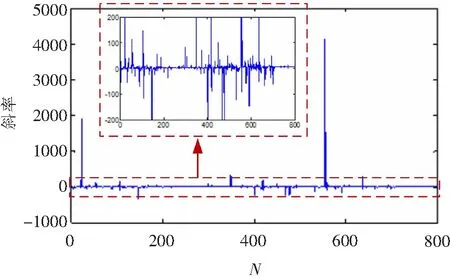
图7 斜率值Fig.7 Slope value

由于斜率和系统阻抗值有关，故文献[19]通过对斜率设定阈值，将不同斜率(系统阻抗)对应的数据点分开。但如图7所示，由于背景谐波电压波动的干扰，导致斜率值波动较剧烈，无法通过斜率正确辨识系统阻抗真实值，故方法2失效。

由图6可以看到散点图呈3个长条状分布，分别对应3个可能的阻抗值，采用文中方法提出方法(DBSCAN法)对散点图进行聚类分析，获得聚类效果对比见图8。

由图8可知，所提出的DBSCAN法能将图6中的3簇数据正确分开，这与仿真设置的2次阻抗变化点相对应。为了验证提出方法的有效性，并在DBSCAN聚类的基础上做进一步系统阻抗估算实验。

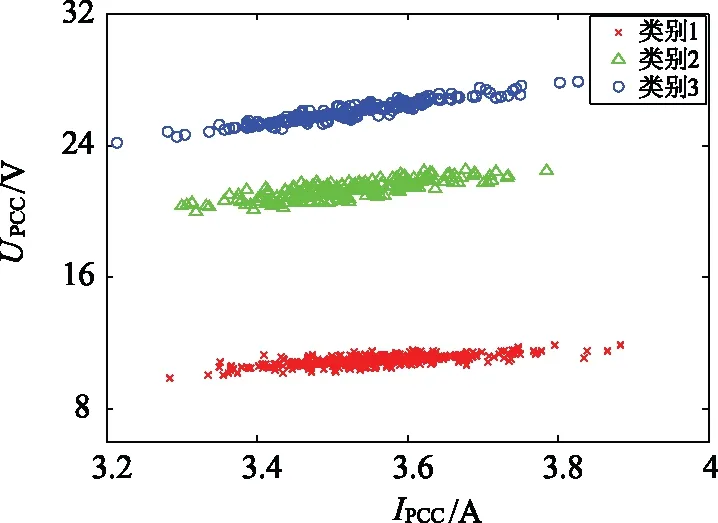
图8 DBSCAN聚类结果Fig.8 DBSCAN clustering results

3.2 系统阻抗估算

对DBSCAN聚类后的数据分别采用波动量法(方法3)、偏最小二乘法(方法4)计算系统阻抗值，并对DBSCAN聚类后的数据进行复相关性分析，筛选出系数高于0.9的数据段，再用稳健回归法估算系统阻抗值(方法5/文中方法)。计算结果如表1所示，并计算相对误差如表2所示。

表1 谐波阻抗估算结果Tab.1 Estimation results of harmonic impedance

表2 谐波阻抗估算误差Tab.2 Estimation error of harmonic impedance

由表2可知，方法5(文中方法)估计系统阻抗值的误差最小，验证了所提出的DBSCAN聚类、复相关性分析筛选和基于bisquare权重的稳健回归法估计系统阻抗方法的有效性。

4 结束语

文章综合考虑了系统阻抗变化和背景谐波电压波动的情况，提出谐波阻抗估算新方法。对谐波电压和谐波电流的散点图进行DBSCAN聚类分析，将不同谐波阻抗对应的数据组分离，进行复相关性分析，筛选出背景谐波电压较稳定的数据段，采用基于bisquare权重的稳健回归法进行系统阻抗估算。仿真表明，当系统阻抗变化时，所提出的DBSCAN聚类方法能有效分离系统阻抗恒定的数据段，所提出复相关性分析筛选法和基于bisquare权重的稳健回归法能进一步提高系统阻抗估计的精度，提出方法适用条件更广，有一定的应用价值。